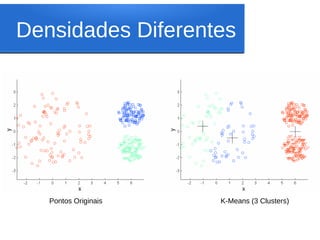
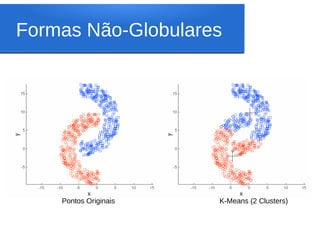
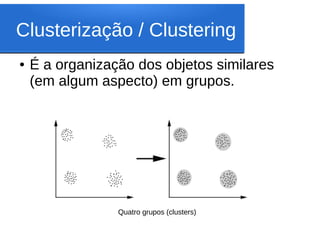
Este documento discute o algoritmo K-means de clusterização. Ele descreve a história do K-means, incluindo suas origens na década de 1950 e o primeiro uso do termo por James MacQueen em 1967. Também explica os conceitos-chave por trás do K-means, como espaço euclidiano, distância euclidiana, centróides e clusterização. Finalmente, apresenta os passos do algoritmo K-means básico.














![Pseudo-Código
● K-Means({x1, x2, ..., xn},K,A) #entrada
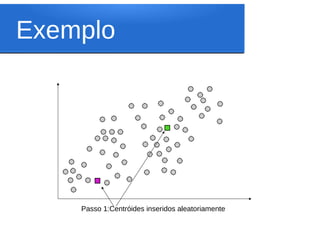
(c1, c2, ..., cK) <--- cria_centroids({x1, x2, ..., xn}, K) #criando k
centróides
Para cada cluster K faça:
uk <--- ck #atribuindo cada centróide a um cluster
enquando o criterio de parada não for atingido faça: #por exmeplo,
enquando houver modificações nos clusters ou um trocou=true
para cada cluster K faça:
cluster[k] = {}
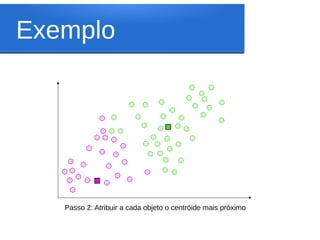
para cada ponto P faça: #o total de pontos é n
atribui_ponto_ao_cluster(P, A, cluster) #calcula-se a distância do
ponto ao centróide de cada cluster e este ponto irá permanecer no cluster que
tiver a menor distância
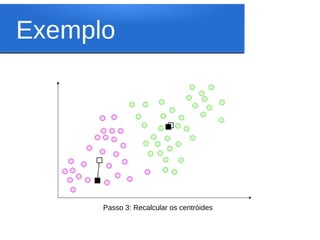
para cada cluster K faça:
uk <-- novo_centroid(K) #recalculando os centródes
●
return {u1, u2, ..., uk}](https://image.slidesharecdn.com/kmeans-130216101207-phpapp01/85/Kmeans-16-320.jpg)