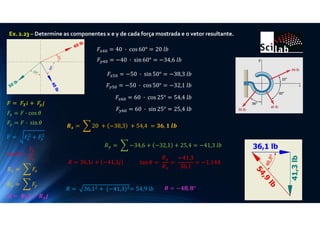
O documento apresenta dois exemplos de resolução de problemas envolvendo forças. No primeiro exemplo, são dadas quatro forças e calculado o vetor resultante. O segundo exemplo apresenta seis forças e também calcula o vetor resultante. Ambos os exemplos utilizam fórmulas trigonométricas para decompor as forças em componentes x e y e somá-las para obter o vetor resultante final.

1. Ex. 2.23 – Determine as componentes x e y de cada força mostrada e o vetor resultante.
𝐹 = 𝐹 𝑖 + 𝐹 𝑗
𝐹 = 𝐹 cos 𝜃
𝐹 = 𝐹 sin 𝜃
tan 𝜃 =
𝐹
𝐹
𝐹 = 𝐹 + 𝐹
𝑅 = 𝐹
𝑅 = 𝐹
𝑹 = 𝑹 𝑿 𝒊 + 𝑹 𝒚 𝒋
𝐹 = 40 cos 60° = 20 𝑙𝑏
𝐹 = −40 sin 60° = −34,6 𝑙𝑏
𝑹 𝒙 = 20 + −38,3 + 54,4 = 𝟑𝟔, 𝟏 𝒍𝒃
𝑅 = −34,6 + −32,1 + 25,4 = −41,3 𝑙𝑏
𝐹 = −50 sin 50° = −38,3 𝑙𝑏
𝐹 = −50 cos 50° = −32,1 𝑙𝑏
𝐹 = 60 cos 25° = 54,4 𝑙𝑏
𝐹 = 60 sin 25° = 25,4 𝑙𝑏
𝑅 = 36,1𝑖 + −41,3𝑗
𝑅 = 36,1 + (−41,3) = 54,9 𝑙𝑏
tan 𝜃 =
𝑅
𝑅
=
−41,3
36,1
= −1,144
𝜽 = −𝟒𝟖, 𝟖°

2. Ex. 2.24 – Determine as componentes x e y de cada das forças mostradas e o vetor resultante.
𝐹 = 𝐹 𝑖 + 𝐹 𝑗
𝐹 = 𝐹 cos 𝜃
𝐹 = 𝐹 sin 𝜃
tan 𝜃 =
𝐹
𝐹
𝐹 = 𝐹 + 𝐹
𝑅 = 𝐹
𝑅 = 𝐹
𝑹 = 𝑹 𝑿 𝒊 + 𝑹 𝒚 𝒋
𝐹 = 80 cos 40° = 61,3 𝑁
𝐹 = 80 sin 40° = 51,4 𝑁
𝐹 = 120 cos 70° = 41,0 𝑁
𝐹 = 120 sin 70° = 112,8 𝑁
𝐹 = −150 cos 35° = −122,9 𝑁
𝐹 = 150 sin 35° = 86 𝑁
𝑹 𝒙 = 61,3 + 41,0 + −122,9 = −𝟐𝟎, 𝟔 𝑵
𝑅 = 51,4 + 112,8 + 86 = 250,2 𝑁
𝑅 = −20,6𝑖 + 250,2j
𝑅 = (−20,6) + 250,2 = 251,05
tan 𝜃 =
𝑅
𝑅
=
250,2
−20,6
= −12,146
𝜽 = −𝟖𝟓, 𝟑°