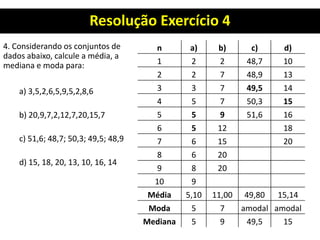
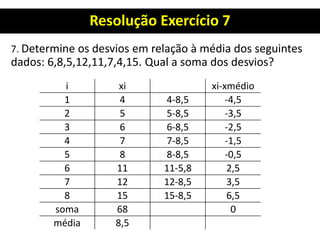
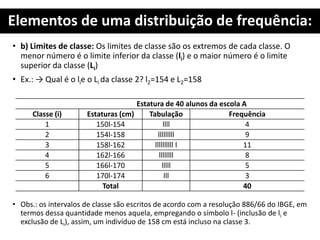
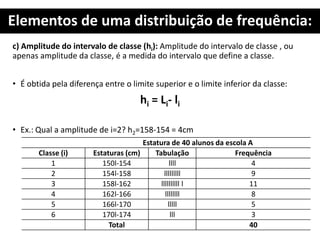
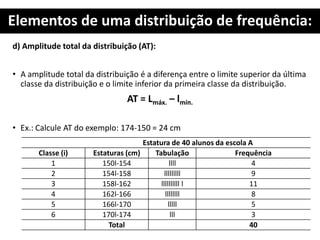
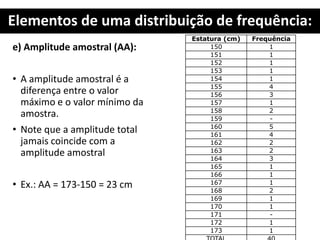
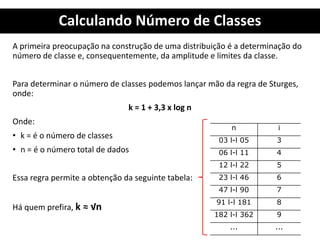
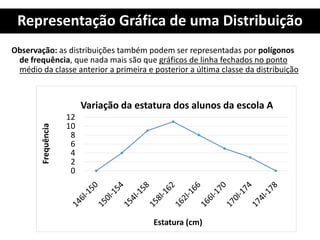
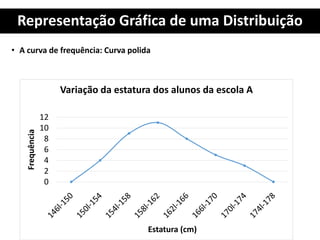
1. O documento apresenta os conceitos fundamentais de estatística para análise de qualidade, incluindo tabelas primitivas, distribuição de frequência, elementos de uma distribuição de frequência e cálculo de número e intervalos de classes.
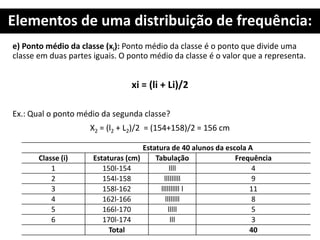
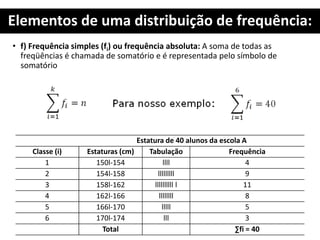
2. São explicados termos como ROL, amplitude total, amplitude amostral, ponto médio da classe e frequência simples.
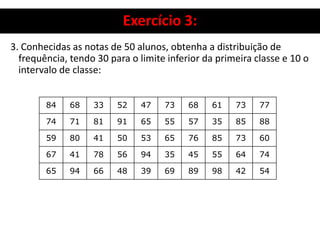
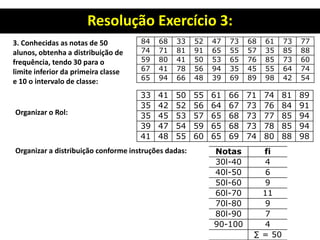
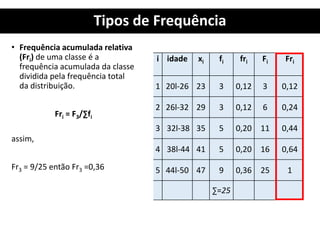
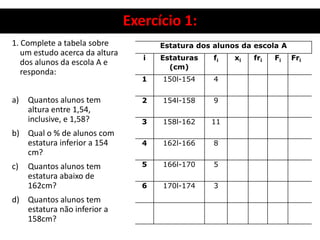
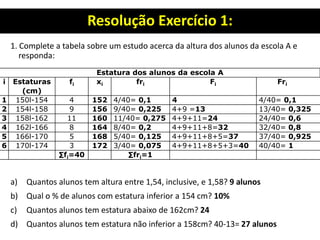
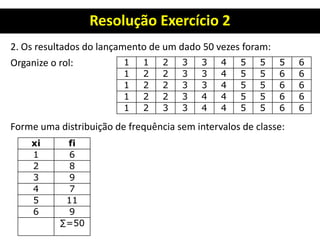
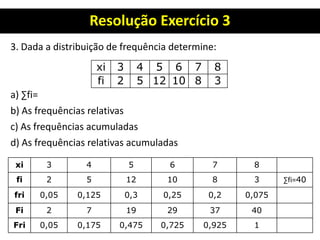
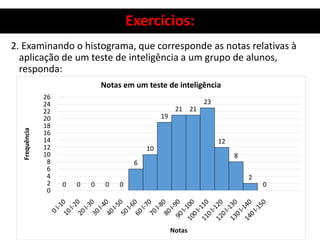
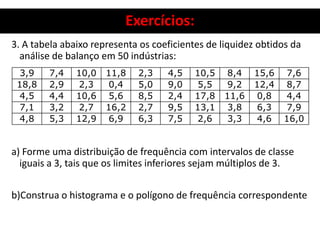
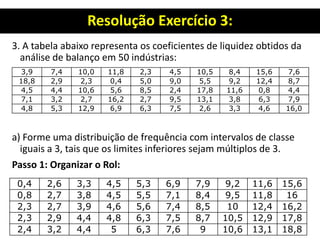
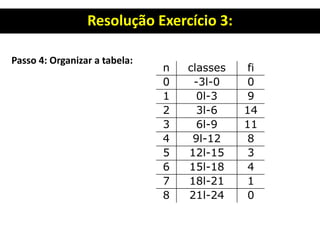
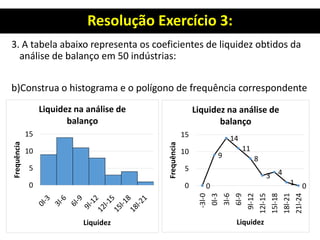
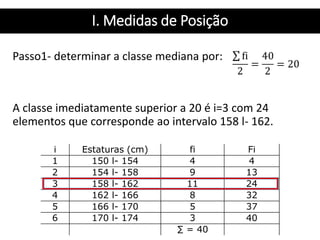
3. Há também um exercício resolvido passo a passo sobre organização de dados, construção de distribuição de frequência e cálculo de seus elementos.






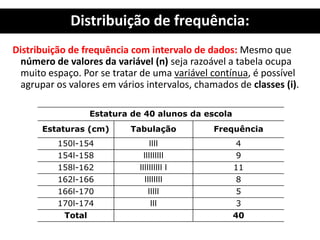

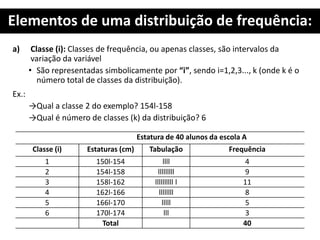
















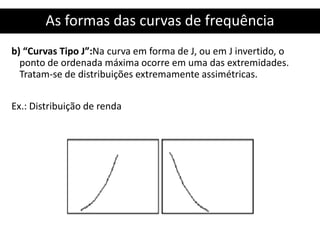
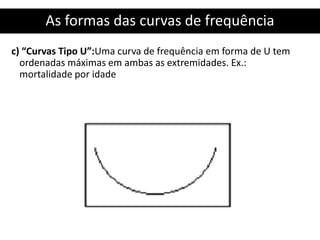
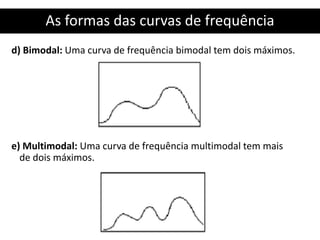
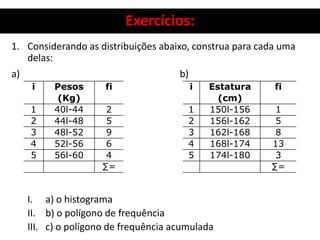



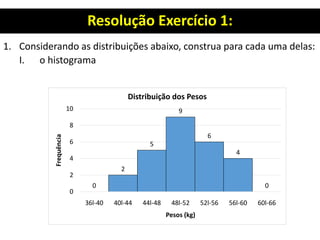
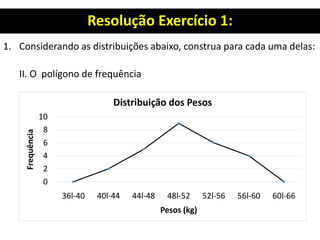
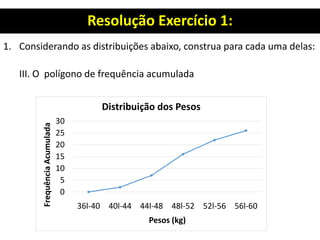

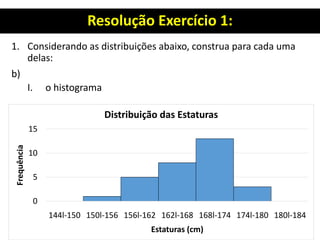
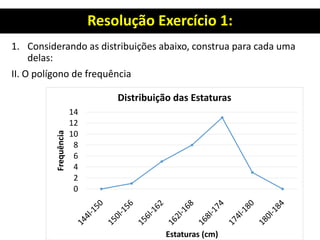
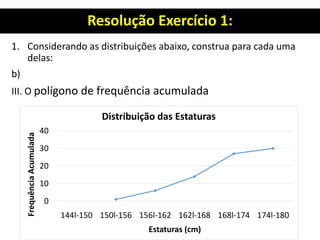







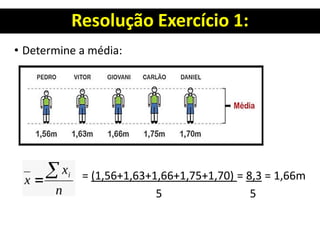






























![Resolução Exercício 1
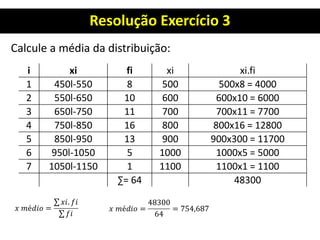
1. Calcule a média aritmética pelo processo breve:
Custos
(R$)
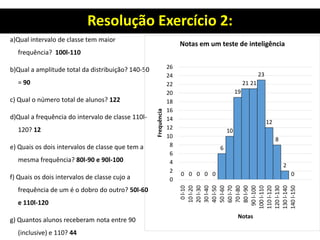
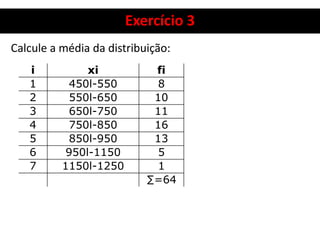
450 l- 550 l- 650 l- 750 l- 850 l- 950 l- 1050 l- 1150
fi 8 10 11 16 13 5 1
i xi fi yi yifi
R.: xmédio = 800 + [(-29)x100] /64
=800 +[-2900/64]
=800 – 45,31
xmédio = 754,69
1 500 8 -3 -24
2 600 10 -2 -20
3 700 11 -1 -11
4 800 16 0 0
5 900 13 1 13
6 1000 5 2 10
7 1100 1 3 3
∑=64 ∑=-29](https://image.slidesharecdn.com/aula17-25-estqual-professor-240111182907-51029cac/85/Aula-17-25-Est-Qual-PROFESSOR-pdf-116-320.jpg)