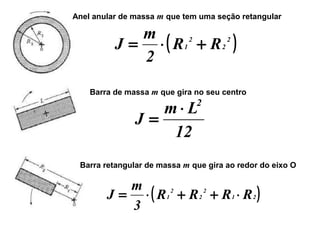
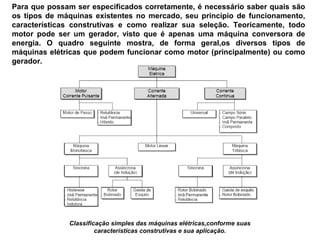
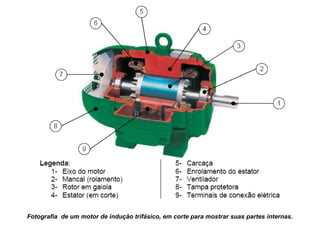
O documento descreve os principais tipos de máquinas elétricas girantes, incluindo suas partes e operações. É apresentada uma classificação simples destas máquinas de acordo com suas características construtivas e aplicações, distinguindo entre rotores de pólos salientes e lisos. Também são definidos conceitos-chave como estator, rotor, isolamento e enrolamento amortecedor.

1. MÁQUINAS
ELÉTRICAS
GIRANTES

2. INTRODUÇÃO
Máquinas elétricas são máquinas destinadas a transformar a energia elétrica em
energia mecânica e vice-versa. Como vimos anteriormente, elas podem ser
classificadas segundo a transformação da energia: geradora, motora ou
transformadora. As duas primeiras classificações são também chamadas de
"máquinas elétricas girantes ou rotativas", pela própria característica da
conversão eletromecânica.
Nestes tipos de máquinas girantes ou rotativas, suas operações podem ser
como operação MOTORA ou operação GERADORA. O que diferencia uma
máquina da outra é o sentido da energia empregada. Por exemplo: quando se
recebe energia mecânica rotacional pelo eixo da máquina e se converte em
energia elétrica, temos então um gerador. A mesma máquina, com algumas
adaptações, poderá receber energia elétrica e convertê-la em energia mecânica
rotacional. Neste caso, teremos um motor.
Possíveis operações de uma máquina elétrica rotativa.

3. Para que possam ser especificados corretamente, é necessário saber quais são
os tipos de máquinas existentes no mercado, seu princípio de funcionamento,
características construtivas e como realizar sua seleção. Teoricamente, todo
motor pode ser um gerador, visto que é apenas uma máquina conversora de
energia. O quadro seguinte mostra, de forma geral,os diversos tipos de
máquinas elétricas que podem funcionar como motor (principalmente) ou como
gerador.
Classificação simples das máquinas elétricas,conforme suas
características construtivas e sua aplicação.

4. Esta classificação é a mais conhecida e aceita, podendo as máquinas
elétricas também serem, classificadas segundo o critério de rotação, grau de
proteção, torque, rendimento etc.
DEFINIÇÕES
A máquina rotativa tem partes fixas e partes móveis. A parte fixa (estática)
chamamos de ESTATOR e a parte móvel, girante ou rotativa chamamos de
ROTOR. A figura a seguir mostra as várias partes de um motor elétrico
genérico, no caso um motor trifásico de indução.
O espaço entre o estator e o rotor é chamado de "entreferro“, em Inglês: air
gap, e tem papel fundamental no rendimento da máquina. O rotor
normalmente é montado sobre um eixo de aço que está apoiado sobre
mancais nas duas extremidades da carcaça. Este eixo normalmente recebe
tratamento térmico para evitar problemas de empenamento e fadiga. A
carcaça é a estrutura que suporta todo o conjunto e são geralmente de
construção robusta em ferro fundido, aço ou alumínio, dependendo da
aplicação.
O rotor pode ser um núcleo composto de chapas de material ferromagnético,
a fim de reduzir as perdas no ferro, ou de uma peça fundida em alumínio que
sustenta às chapas de ferro Neste último caso, estamos falando de um rotor
no formato de gaiola no as barras e anéis de Alumínio formam os condutores
do rotor em curto circuito.O rotor em formato de gaiola pode ser também
construído com barras anéis de cobre ou ligas de cobre. Na prática, o projeto
e a construção do rotor depende da sua aplicação e das características
necessárias para seu melhor funcionamento.

5. Fotografia de um motor de indução trifásico, em corte para mostrar suas partes internas.

6. Num gerador síncrono por exemplo, num turbogerador o rotor poderá ser
uma peça maciça ferromagnética, usinado de forma a se criar ranhuras,
slots, em sua superfície que permitam instalar os lados retos das bobinas de
campo, bobinas do rotor.
Rotor cilíndrico de pólos lisos de um turbogerador. Provavelmente um par de
pólos. Repare-se no tamanho da peça em relação ao homem à direita.
Já o rotor de um hidrogerador, normalmente tem-se um diâmetro muito
superior a de um turbogerador. Neste caso, nem todo material do rotor é
peça magnética,sendo o núcleo rotativo composto apenas de uma estrutura
metálica que dá suporte e escoramento ao núcleo magnético propriamente
dito. Nesta estrutura ficam engastadas as peças polares, que são os pólos
do rotor. Mais adiante veremos como é isto e a diferença entre os diversos
tipos de máquinas síncronas

7. Rotor de um hidrogerador. Repare-se no número de pólos salientes, peças
Polares, e no enrolamento de armadura da excitatriz, à esquerda..
No caso do rotor de um motor, o tipo de motor é que define as características
construtivas do rotor, podendo ser de indução (o mais comum), de corrente
contínua, síncrono bobinado, de ímã permanente etc.
Portanto, dependendo do tipo de máquina elétrica elas possuem características
bastantes diferentes, podendo acomodar bobinas, anéis de curto-circuito ou
ímãs permanentes.

8. Um outro dado importante é quando dizemos sobre a velocidade da
máquina. A "velocidade do eixo", "velocidade do rotor" ou "velocidade da
máquina" diz respeito sobre a mesma coisa, ou seja, a velocidade de rotação
do eixo da máquina. Pode parecer infundado o esclarecimento, mas este
tipo de dúvida tem provocado bastante confusão.
Tanto o rotor quanto o estator possuem três partes importantes: o núcleo
magnético, o enrolamento, bobinas, e o sistema de isolação. O propósito do
núcleo é de "canalizar" o fluxo magnético através das bobinas. Os
enrolamentos conduzem correntes elétricas que geram o fluxo magnético
necessário para a conversão da energia, seja de elétrica para mecânica ou
vice-versa. E o sistema de isolação que previne possíveis curto-circuitos nas
partes de contato.
A seguir, veremos mais alguns detalhes sobre o rotor, o estator, o sistema
de isolação e os enrolamentos amortecedores.
ROTOR
Em algumas máquinas, o rotor pode abrigar suas bobinas de duas maneiras
diferentes.Se expusermos os pólos magnéticos ao enrolamento do estator
chamaremos isto de rotor de "pólos salientes". Quando o núcleo do rotor
tem pólos salientes, núcleo polar, as bobinas do rotor são enroladas em
volta desta peça. O conjunto final do pólo é chamado de "sapata polar",
nome muito utilizado no meio industrial. Sua função é providenciar uma
correta distribuição da densidade de fluxo através do entreferro.

9. Rotor de pólos salientes. Fotografia do rotor de um grande motor esquerda. Repare-se nos detalhes
construtivos deste tipo de conjunto. À direita, desenho esquemático mostrando o rotor de 4 pólos e as
linhas de campo percorrendo seu caminho magnético. Observe-se as bobinas de campo, formato
retangular, envolvendo os pólos e o sentido das correntes.
Os pólos salientes são usados principalmente em máquinas síncronas de geração de
energia e também na parte estatórica das máquinas de corrente contínua Estas
máquinas geralmente trabalham com rotações baixas, devido à resistência do ar
elevado, ao conjunto mecânico não muito sólido e ao elevado número de pólos.
Na geração de energia hidrelétrica, a maioria das turbinas hidráulicas trabalham com
uma velocidade baixa de rotação,entre 50 e 300 RPM a fim de obter a máxima
performance do aproveitamento hidráulico. Como a freqüência elétrica é fixa 60 Hz, o
número de pólos será um número relativamente grande. Baixa rotação geralmente
caracteriza um diâmetro D de rotor elevado, de forma a fornecer espaço suficiente para
a colocação de todos estes pólos,e um comprimento L dos pólos pequeno em relação a
este diâmetro.

10. Rotor de pólos lisos. À esquerda temos detalhes das ranhuras do rotor de um turbogerador. À direita, um
desenho esquemático mostrando o rotor de pólos lisos e as linhas de campo percorrendo seu caminho
magnético.
A outra maneira de se abrigar as bobinas do rotor e produzir pólos magnéticos é
chamado de "pólos lisos". Neste caso, o bobinado do rotor está embutido nas
ranhuras, slots, da mesma. Como vimos anteriormente, os turbogeradores são
geradores que possuem este tipo de rotor. Sua energia mecânica, de rotação advém
de turbinas à vapor que trabalham em altíssimas rotações. É o caso típico encontrado
na co-geração em usinas de
açúcar e álcool. Esta rotação vai de 1500 a 3600 RPM, o que significa que o gerador
deverá dar conta desta velocidade. Como são máquinas síncronas, ou seja, trabalham
numa rotação sincronizada com a freqüência elétrica nominal, o número de pólos é
sempre muito baixo, não excedendo a 4. Portanto, as máquinas síncronas de geração
turbinada à vapor possuem 2 ou 4 pólos apenas.

11. Diferentemente das máquinas de pólos salientes, as de pólos lisos geralmente tem
diâmetro D pequeno e comprimento L grande, ou seja, a relação D / L sempre será
menor que 1. Ao contrário das de pólos salientes, onde esta relação sempre será maior
que 1.
Em resumo
Turbinas hidráulicas tipo, Kaplan ou Francis, oferecem rotações baixas no
seu eixo, exigindo uma máquina, hidrogerador, com vários pólos magnéticos,
de preferência pólos salientes, o que implica num diâmetro grande,
comparado ao seu menor comprimento.
Já as turbinas à vapor oferecem alta rotação, exigindo máquinas elétricas de
pouquíssimos pólos, no máximo 4, embutidos na própria peça rotórica pólos
lisos. Isto implica num diâmetro menor que o seu comprimento,
caracterizando um turbogerador.
ESTATOR
Como vimos anteriormente, o estator é a parte estática de uma máquina elétrica. É
composta pela carcaça, pelo núcleo magnético e pelos enrolamentos do estator. No
caso de um hidrogerador, a carcaça é fabricada em chapas de aço soldadas e podem
ser construídas em seções para facilitar o manuseio e o transporte. O núcleo do estator
é constituído de lâminas de 0,35 a 0,50 mm de espessura, de aço silício de alta
permeabilidade. São estampadas com a máxima precisão, isentas de rebarbas e
envernizadas em ambos os lados e curados a altas temperaturas.
No estator estão distribuídos, por suas ranhuras, os lados retos das bobinas de campo
(para motores) ou bobinas de armadura, para geradores, conforme mostra a figura. Do
ponto de vista elétrico, o estator de um gerador é idêntico ao estator de um motor de
indução trifásico.

12. Exemplo do estator de um motor
síncrono.Observe-se as cabeças das
bobinas de campo como estão
escamoteadas para fora do corpo
estatórico.
Exemplo de uma lâmina estatórica. A sua montagem
circular formará o núcleo magnético do estator.
Para grandes máquinas, geradora ou motora, o núcleo estatórico é formado
por uma combinação de chapas segmentadas, colocadas lado a lado, de tal
forma a constituir uma peça única Este tipo de construção é muito comum
na montagem de hidrogeradores.
ISOLAÇÃO
O sistema de isolação previne que possíveis curto-circuitos ocorram. Estão
em várias partes da máquina elétrica, estator e rotor como entre as espiras
de uma bobina, entre bobinas e o núcleo magnético, entre bobinas e a
carcaça, etc. As isolações protegem contra surtos de chaveamento e outros
tipos de defeitos. Também são elementos importantes na proteção térmica e
seus efeitos.

13. Alguns especialistas colocam o sistema de isolação como o principal
elemento de uma máquina elétrica. Seu funcionamento é fundamental no
desempenho e nas características de funcionamento de uma máquina
elétrica. Um sistema de isolação precário compromete não só o
funcionamento da mesma como também o sistema de alimentação de
energia como um todo.Existem diversos materiais de isolação que suportam
altas temperaturas sem perder suas principais características de isolação,
como por exemplo o papel Kraft, o MYLAR® e o NOMEX® da DuPont.
Exemplo de aplicação do NOMEX® nas ranhuras de um motor. Observe-se que ele isola
completamente os fios da bobina em relação ao anel estatórico.

14. ENROLAMENTO AMORTECEDOR
Como já vimos, uma máquina elétrica possui dois enrolamentos básicos, um
conjunto de enrolamentos do estator e um conjunto de enrolamentos do
rotor. Existe ainda um terceiro enrolamento colocado no rotor na máquina
síncrona de pólos salientes, formado por barras, em geral de cobre, que
estão curto-circuitadas através de dois anéis como se fosse uma gaiola de
esquilo e inseridas em ranhuras feitas na superfície dos pólos. Este
enrolamento especial chamamos de enrolamento amortecedor. Sua função é
a de amortecer oscilações de conjugado-mecânico do rotor que poderiam
provocar quebras de sincronismo e causar a saída da máquina, uma vez que
fora do sincronismo esta deixa de produzir torque útil. Além disso, o
enrolamento amortecedor pode reduzindo sobretensões momentâneas,
auxiliar na sincronização quando ocorre alguma falha na máquina ou no
sistema ao qual ela está ligada etc. Quando a máquina está como motor,
este enrolamento permite a partida dela como motor, funcionando como se
fosse um motor de indução normal
Desenho esquemático dos pólos salientes de um rotor.
Repare-se nos detalhes das barras amortecedoras na
cabeça dos pólos,curtocircuitadas por um par de
anéis.
Fotografia de um rotor que mostra, no detalhe, as barras
amortecedoras.

15. CONCEITOS ELEMENTARES
Para o bom entendimento das características e das funcionalidades das
máquinas elétricas, necessário se faz apresentar alguns conceitos
elementares que ajudarão a entender tais características e o funcionamento.
TORQUE OU CONJUGADO
O torque, também chamados de momento ou binário, é a medida do esforço
necessário para girar um eixo qualquer. Por definição, torque é o produto da
força aplicada, em newtons,pela distância perpendicular entre o eixo de
rotação e o ponto de aplicação desta força. A figura ajuda a entender melhor
esta definição.
O desenho mostra que se aplicarmos uma força F tangencial à roda, de
raio r, teremos um torque desenvolvido sobre a roda em seu eixo axial.
O torque ζ é dado por:
rF ⋅=τ
Onde: ζ = Torque, em N.m
F = Força tangencial, em newton
r = raio, em metros.

16. Exemplo
Um motor desenvolve um torque inicial de 350 Nm. Se a polia que está
engastada no seu eixo tem um diâmetro 1,5 m, calcule a força de frenagem
necessária para evitar a rotação do motor.
1,5m
67,466
2
5,1
350
F
r
FrF
==
=⇒⋅=
τ
τ
Nm
TRABALHO MECÂNICO
O trabalho mecânico existe sempre que uma força ´F´ aplicada sobre um
corpo provoca um deslocamento ´d´ na mesma direção de F.
Resposta

17. O trabalho mecânico W é dado por:
dFW ⋅=Onde:
W = Trabalho, em joule
F = Força, em newton
d = deslocamento, em metros
Exemplo
Uma massa de 45 kg foi erguida a uma altura de 15 metros. Calcule o trabalho
realizado.
15 m
Resposta
45,44181,945FgmF =⋅=→⋅= N
75,66211545,441WdFW =⋅=→⋅= J
POTÊNCIA MECÂNICA
A potência mecânica é o trabalho mecânico realizado numa determinada
quantidade de tempo. A unidade da potência mecânica, no sistema
internacional SI, é o watt W.

18. t
W
Pmec
∆
=
Onde:
W= Trabalho mecânico, em joule
t = tempo, em segundos.
Exemplo
Um motor elétrico ergue uma carga de 50 kg a uma altura de 20 metros em 7
segundos. Calcule o trabalho mecânico realizado e a potência mecânica
entregue pelo eixo do motor.
20 m
gmF ⋅=
Solução
e dFW ⋅=
98102081,950dgmW =⋅⋅=⋅⋅= Joules
43,1401
7
9810
t
W
Pmec ===
∆
watts
Usualmente, a potência mecânica pode ser expressa
em cavalo-vapor CV ou em horse-power HP. Desta
forma, a relação com a potência em watt é:
Watts736.......CV1 Watts746.......HP1e

19. Assim a potência mecânica no eixo do motor para o exemplo anterior seria,
CV2CV9,1
736
43,1401
Pmec ≈== ou HP2HP88,1
746
43,1401
Pmec ≈==
Se analisarmos as equações anteriores verificamos que:
A parcela d/Δt na verdade é a velocidade com que o deslocamento do
corpo ocorre Se supormos que no exemplo anterior o eixo do motor
contivesse uma polia de raio ´r´, girando a ´n´ RPM, teríamos uma
velocidade tangencial v na polia definida como:






⋅=
⋅
==
t
d
F
t
dF
t
W
Pmec
∆∆∆
rv ⋅= ω
Como
f2 ⋅⋅= πω e
60
n
f = para rotações por minuto
então n
3060
n
2 ⋅





=⋅⋅=
π
πω daqui rn
30
rv ⋅⋅





=⋅=
π
ω
Onde:
v = velocidade tangencial, em m/s
n = numero de rotações por minuto RPM
r = raio da polia, em metro

20. Neste caso, teremos para a potência mecânica Pmec a seguinte expressão:
vFP
t
d
FP mecmec ⋅=→





⋅=
∆
Exemplo
Um motor elétrico ergue uma carga de 50 kg a uma altura de 20 metros em 7
segundos,se o motor tem uma polia com Ø = 12 cm no seu eixo, qual seria a
rotação ideal para subir a carga no tempo prescrito ?
Solução:
A velocidade de subida da carga é igual a velocidade tangencial da corda
na polia
86,2
7
20
t
d
v === m/seg
73,454
06,0
30
86,2
r
30
v
nrn
30
v =
⋅





=
⋅





=→⋅⋅





=
ππ
π
RPM

21. POTÊNCIA ELÉTRICA
Um sistema elétrico compostos por cargas passivas, resistores, capacitores
e indutores,acoplado a uma fonte de tensão variável v(t), faz circular uma
corrente i(t) também variável.
Como sabemos, a potência instantânea num sistema elétrico é dado por:
)t(i)t(v)t(p ⋅= W
Pela convenção de sinais, uma potência com sinal positivo corresponde a
uma transferência de energia da fonte para a carga. Para uma potência com
sinal negativo ocorre o inverso, ou seja, um retorno de energia da carga para
a fonte.
No caso de uma carga puramente indutiva, uma tensão senoidal,
( )tcosV)t(v máx ω⋅=
aplicada à carga resulta numa corrente senoidal atrasada de 90º, ou
)º90tcos(I)t(i áxm −⋅= ω
Logo, a potência elétrica instantânea passa a ser:
)º90tcos()tcos(IV)t(i)t(v)t(p áxmmáx −⋅⋅⋅=⋅= ωω
)t2(senIV
2
1
)t(p áxmmáx ω⋅⋅⋅=

22. Potência Ativa
V
I
P
V
I
CIRCUITO RESISTIVO R
ϕcosIVP ⋅⋅=

23. V
Potência reativa
V II
CIRCUITO INDUTIVO L
ϕsenIVQ ⋅⋅=

24. V
I
Potência reativa
CIRCUITO CAPACITIVO C
ϕsenIVQ ⋅⋅=

25. V
I
Potência Aparente
Potência Ativa
Potência Reativa
PQ
CIRCUITO MISTO R L C
IVS ⋅=
ϕcosIVP ⋅⋅=
ϕsenIVQ ⋅⋅=

26. Gráfico de tensão e corrente senoidal.
Em vermelho a potência instantânea. Repare-se
que a potência possui o dobro da freqüência da
corrente.
Se analisarmos a figura veremos
que no intervalo entre 0< ωt < π/2,
a potência p(t) é positiva, pois a
tensão e a corrente tem os
mesmos sinais e portanto a fonte
está entregando potência para a
carga.
No intervalo π/2 < ωt < π a potência
é negativa,tensão e corrente tem
sinais contrários e aí a carga
fornece potência à fonte. Nesta
fase, significa que a carga indutiva
está descarregando sua energia
armazenada na fase anterior.
Observe-se que neste um ciclo de
0 a π a potência média é zero.
No caso mais geral, a carga ligada à fonte tem uma impedância Z = R +jX ou
Z = |z|. /θ , onde θ é o ângulo entre os vetores R e X, dado por arctg (X/R).
Neste caso, uma tensão v(t)= Vmax. cos(ωt) aplicada nesta carga resulta
numa corrente i(t)= Imax. cos(ωt - θ), onde θ pode ser positivo ou negativo,
correspondendo à impedância equivalente indutiva ou capacitiva.

27. Temos
θcosIVP efefef ⋅⋅=
Como sabemos que o produto da tensão eficaz Vef pela corrente eficaz Ief é
a Potência Aparente S. Então, temos que:
θθθ cosSPefcosScosIVP efefef ⋅=→⋅=⋅⋅=
Neste caso, a potência eficaz de um circuito qualquer é o que chama-se de
POTÊNCIA ATIVA.
Ao fazer uma relação de potências entre P e S veremos que isto dá o que
chama-se de fator de potência FP:
=→= θθ cos
S
P
cos
med
FATOR DE POTÊNCIA
Portanto, o fator de potência é dado pela relação dentre a potência média
potência Ativa P e a potência Aparente S.
Para um circuito trifásico qualquer, a potência aparente é a soma das
potências aparentes de cada fase, ou seja:
fasefase IV3S ⋅⋅=
Entretanto, como os sistemas trifásicos são ligados em delta Δ ou estrela Y,
as tensões e correntes são calculadas pelas suas tensões de linha ou
corrente de linha. Neste caso, a potência aparente passa a ser calculada
por:
linhalinha IV3S ⋅⋅=

28. RENDIMENTO DOS MOTORES ή
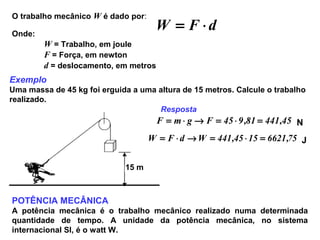
Um motor elétrico absorve energia elétrica da rede e a transforma em
energia mecânica disponível no eixo. O rendimento desta máquina define a
eficiência com que é feita esta transformação. Seu cálculo é dada pela
relação entre a potência útil entregue ao eixo potência mecânica e a
potência ativa retirada da rede potência elétrica:
ϕϕ
η
cosIV3
P1000
cosIV3
P736
P
P kWCV
Elétrica
Mecânica
⋅⋅⋅
⋅
=
⋅⋅⋅
⋅
==
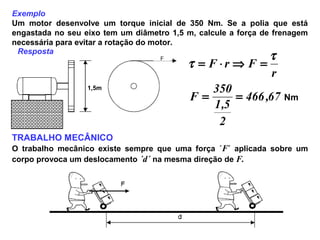
RELAÇÃO ENTRE TORQUE OU CONJUGADO E POTÊNCIA
Quando a energia mecânica é aplicada sob a forma de movimento rotativo, a
potência desenvolvida depende do Torque ζ e da velocidade de rotação n.
As relações entre si são:
ω
τ
WattsP
= Newtons metro [Nm]
Onde:
P =Potência em watts
ω =Velocidade angular em Radianos/segundo
ζ = Torque em Newtons metro
Com a rotação n em rotações por minuto RPM,
60
2
n
π
ω
⋅
⋅= em Rad/seg

29. Assim:
)tcos()tcos(IV)t(i)t(v)t(p áxmmáx θωω −⋅⋅⋅=⋅=
( ) ( ){ }βαβαβα −++=⋅ coscos
2
1
coscosComo,
( ) ( ) ( ) ( ){ }θθωθωω cost2cos
2
1
tcostcos +−=−⋅⇒
Pode-se demonstrar que cos(2ωt – θ) tem um valor médio igual a zero.
Portanto,
: ( ) ( )θωω −⋅⋅⋅= tcostcosIV)t(p áxmmáx
Esta é a potência média para qualquer θ. Portanto:
θcosIV
2
1
)t(p áxmmáx ⋅⋅⋅=
θcosIV
2
1
P áxmmáxmed ⋅⋅⋅=
Como
efmáx V2V ⋅= e efáxm I2I ⋅=

30. Se a potência do motor está em CV e a rotação em RPM,
60
2
n
P736 CV
π
τ
⋅
⋅
⋅
=
A fração
28,7028
60
2
736
=
⋅π
daqui
n
28,7028PCV ⋅
=τ
Se a potência do motor está em kW e a rotação em RPM,
60
2
n
P1000 kW
π
τ
⋅
⋅
⋅
=
A fração
daqui
n
30,9549PkW ⋅
=τ30,9549
60
2
P1000 kW
=
⋅
⋅
π

31. A potência então relaciona-se com o torque,
ωτ ⋅=P
O torque em Nm e ω em Rad./seg →P resultará em Watts
28,7028
n
P
RPMNm
CV
⋅
=
τ
CV
30,9549
n
P
RPMNm
kW
⋅
=
τ
kW
EXEMPLO
Calcular o torque nominal de um motor de 10CV e 1750 RPM
16,40
1750
28,702810CV
=
⋅
=τ Nm
( ) 16,40
1750
30,9549736,010
=
⋅⋅
=τ Nm
16,40
60
2
1750
73610
=
⋅
⋅
⋅
=
π
τ Nm

32. ENERGIA CINÉTICA DE ROTAÇÃO E MOMENTO DE INÉRCIA
A queda de uma pedra ou o movimento de um carro possuem ambos energia
cinética,que é a energia devido ao movimento. A energia cinética é uma
forma de energia mecânica e é dada pela equação :
2
c vm
2
1
E ⋅⋅=
onde:
Ec = energia cinética, em Joule (J)
m = massa do corpo, em kg
v = velocidade do corpo, em m/s
Um corpo em rotação também possui energia cinética. Sua magnitude
depende também da velocidade de rotação e da massa corporal. Só que
neste caso, a forma do corpo influencia diretamente no resultado.
Para se determinar a energia cinética de um corpo em rotação, usa-se a
equação :
( ) J
1800
n
E
2
c ⋅
⋅
=
π
onde:
n = Velocidade rotacional, em RPM
J = Momento de inércia, em kg.m²

33. O momento de inércia J, ou simplesmente "inércia" depende da massa e do
formato do corpo, geometria para ser determinado. A relação a seguir
mostra algumas formas geométricas mais comuns para se determinar sua
inércia. Caso o corpo tenha uma estrutura mais complexa, segmenta-se esta
estrutura em estruturas mais conhecidas, conforme a relação anterior. O
momento de inércia total será a soma dos momentos de inércia de cada
corpo.
Eixo de
giro
Massa m que gira a uma distância r ao redor de eixo o
2
rmJ ⋅=
Disco sólido de massa m e rádio r
2
rm
J
2
⋅
=

34. Anel anular de massa m que tem uma seção retangular
( )2
2
2
1 RR
2
m
J +⋅=
Barra de massa m que gira no seu centro
12
Lm
J
2
⋅
=
Barra retangular de massa m que gira ao redor do eixo O
( )21
2
2
2
1 RRRR
3
m
J ⋅++⋅=

35. A inércia é um parâmetro importante das máquinas elétricas girantes daí a
necessidade da sua melhor compreensão
Exemplo
Um disco sólido de 1400 kg, diâmetro de 1,0 metro e espessura de 22,5 cm,
gira a 1800 RPM ininterruptamente. Determine seu momento de inércia e a
energia cinética do corpo.
Resposta
O momento de inércia do corpo com esta estrutura é calculada
por:
0,175
2
)5,0(1400
2
rm
J
22
=
⋅
=
⋅
= kgm²
E a energia cinética é então:
( ) ( ) 11,3175
1800
1800
J
1800
n
Ec
22
=⋅
⋅
=⋅
⋅
=
ππ
MJ
O SISTEMA POR UNIDADE p.u.NAS MÁQUINAS ELÉTRICAS
Muito freqüentemente, os cálculos relativos a máquinas, transformadores e
sistemas de potência são efetuados em forma de "por unidade" pu, ou seja,
todas as quantidades envolvidas num cálculo serão expressas como frações
decimais de valores de base convenientemente escolhidas. Portanto, todos
os cálculos serão efetuados em pu, em lugar dos usuais volts, ampéres,
ohms, watts, etc.

36. Há duas vantagens neste sistema. Uma é que as constantes de máquinas e
transformadores caem numa faixa numérica razoavelmente estreita quando
expressas em pu.
A outra é que este método de realizar os cálculos permite a ter uma concreta
sensação da ordem de grandeza do parâmetro, o que ajuda muito na hora de
emitir um juízo sobre um determinado comportamento da máquina.
Todas as grandezas como tensão, corrente, impedância, reatância, etc
podem ser transformadas em pu. Isto se dá da seguinte forma, que já foi
visto:
EXEMPLOS
Dado um valor de tensão-base = 110 V, quais são os valores pu para as
seguintes tensões:
0,4
110
440
440 =→ p.u.
45,3
110
380
380 =→ p.u.
15,1
110
127
127 =→ p.u.
55,0
110
60
60 =→ p.u.
120
110
13200
13200 =→ p.u.
64,103
110
11400
11400 =→ p.u

37. Dado IBASE = 10 A, determine os valores reais das as seguintes correntes
A8,31038,0i.u.p38,0i real =⋅=→=
A64104,6i.u.p4,6i real =⋅=→=

38. FIM