Este documento apresenta uma introdução ao software livre GNU Octave, que possui funcionalidades similares ao Matlab para computação científica e numérica. O documento descreve como instalar e usar o Octave, incluindo operações matemáticas básicas, vetores, matrizes, strings e estruturas de dados.
















![Vetores com mais elementos
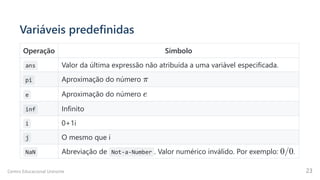
Como exemplo, atribuiremos números de 1 a 5 ao vetor V:
1 > V = [1 2 3 4 5]
V =
1 2 3 4 5
Para acessar cada elemento de V, os parênteses são usados.
V(indice) em que indice é o índice do vetor (começando em 1)
O último elemento pode ser acessado com V(end)
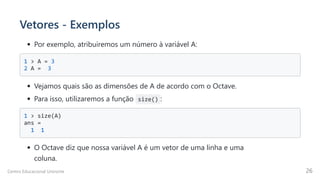
Para o tamanho de V , use size(V) o resultado mostra 1 5 que diz que o vetor
tem uma linha e cinco colunas (vetor-linha)
Centro Educacional Uninorte 27](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-27-320.jpg)
![Vetor-coluna
Iniciamos novas linhas em um vetor usando ponto e vírgula ( ; ). Dessa forma,
podemos definir um vetor com apenas uma coluna, chamado de vetor-coluna:
>> vetor_coluna=[1;2;3;4;5]
vetor_coluna =
1
2
3
4
5
>>
Usando size(vetor_coluna) : 5 1 (cinco linhas e uma coluna)
Centro Educacional Uninorte 28](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-28-320.jpg)
![Matrizes
Podemos criar vetores com números de linhas e colunas diferentes de 1 (que são
as matrizes). Assim
>> A = [1 2 3; 3 2 1; 2 3 1]
A =
1 2 3
3 2 1
2 3 1
>>
As linhas de um vetor devem ter a mesma quantidade de elementos ou será
gerado um erro!
Para acessar um elemento usamos dois índices: A(1,2) 2
→
Centro Educacional Uninorte 29](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-29-320.jpg)




![Matrizes e vetores
A construção de matrizes e vetores no Octave já está inclusa na instalação padrão
do programa.
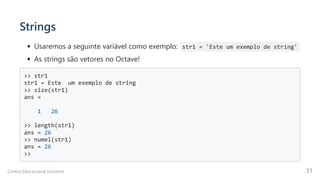
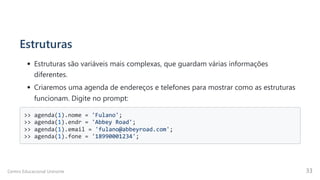
Na sintaxe, o vetor é representado como um conjunto de números, separados em
linhas e colunas, organizados entre [] , de modo que:
A separação por espaço ou vírgula , representa números em uma mesma
linha da matriz;
A separação por ; , nesse caso, representa números em diferentes linhas.
Centro Educacional Uninorte 38](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-38-320.jpg)
![Matrizes e vetores - Exemplo 1
1. Para construir um vetor linha x , basta criar a lista com seus elementos separados
por , ou por espaço :
x=[1,2,3,4]
x =
1 2 3 4
Centro Educacional Uninorte 39](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-39-320.jpg)
![Matrizes e vetores - Exemplo 2
2. Para construir um vetor coluna y , basta criar a lista com seus elementos
separados por ;
(não se preocupe, o ponto e vírgula no final do vetor continua existindo).
y=[1;2;3;4]
y =
1
2
3
4
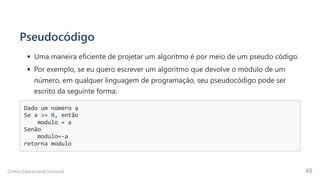
Centro Educacional Uninorte 40](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-40-320.jpg)
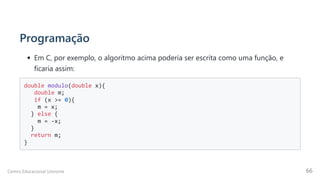
![Matrizes e vetores - Exemplo 3
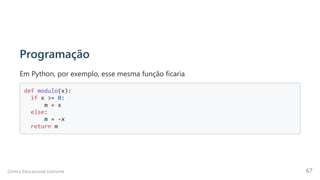
3. Para construir uma matriz M de 3 linhas e 4 colunas , teremos que usar todos os
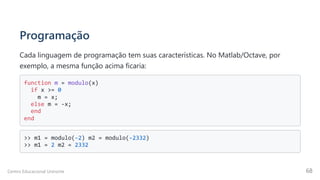
separadores vistos anteriormente:
M = [1 2 3;4,5,6;7,8 9]
%Uma sugestão é fazer da seguinte forma
M = [1 2 3;
4 5 6;
7 8 9];
M =
1 2 3
4 5 6
7 8 9
Centro Educacional Uninorte 41](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-41-320.jpg)
![Matrizes e vetores - Exemplo 4
Obs: O Octave/Matlab aceita variáveis como entrada das matrizes.
Exemplo:
format bank
k=10;
x=sqrt(3)^5;
M = [k k^2 sqrt(k);
x sqrt(x) x/k;
pi 2*pi sin(pi)]
M =
10.00 100.00 3.16
15.59 3.95 1.56
3.14 6.28 0.00
Centro Educacional Uninorte 42](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-42-320.jpg)
![Raízes Reais
Para se encontrar as raízes reais de um polinômio, basta utilizar a função
roots(v) , que retorna em um vetor coluna, as raízes de um polinômio, cujos
coeficientes das potências em ordem decrescente são os elementos do vetor v. -
No exemplo 21, as raízes do polinômio: são -4 e 1
>> roots([1,3,-4])
ans =
-4
1
>>
x +
2 3x − 4
Centro Educacional Uninorte 43](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-43-320.jpg)
![Algumas funções nativas do Matlab/Octave - 1
zeros(m,n) : retorna uma matriz nula com m linhas e n colunas.
ones(m,n) : retorna uma matriz com todos os elementos igual a 1, com m linhas
e n colunas.
eye(m,n) : retorna uma matriz com a diagonal principal com elementos iguais a 1
e os outros elementos iguais a zero, com m linhas e n colunas.
length(A) : retorna o número de elementos no vetor A.
size(A) : retorna um vetor linha [m,n] onde m e n representam a dimensão da
linha e coluna respectivamente.
reshape(A,m,n) : rearranja uma matriz A com r linhas e s colunas para m linhas
e n colunas. r vezes s deve ser numericamente igual a m vezes n.
Centro Educacional Uninorte 44](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-44-320.jpg)

![Algumas funções nativas do Matlab/Octave - 3
median(A) : se A é um vetor, retorna o valor mediano dos elementos do vetor.
mean(A) : se A é um vetor, retorna o valor médio dos elementos do vetor. Se A é
uma matriz retorna um vetor linha com a media de cada coluna.
sort(A) : se A é um vetor, ordena os elementos de A na ordem crescente. Se A é
uma matriz, ordena os elementos de cada coluna.
C = max(A) : se A é um vetor, C receberá o maior elemento de A. Se A é uma
matriz, C é um vetor linha contendo o maior elemento em cada coluna de A.
[d n]=max(A) : se A é um vetor, d recebe o maior elemento de A e n indica a
posição desse elemento no vetor (a primeira posição, caso o elemento não seja
único).
Centro Educacional Uninorte 46](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-46-320.jpg)
![Algumas funções nativas do Matlab/Octave - 4
min(A) : semelhante à função max(A), porém retorna o minimo.
[d,n]=min(A) : semelhante à função [d,n]=max(A), porém retorna o minimo.
sum(A) : se A é um vetor, retorna a soma dos elementos do vetor. Se A é uma
matriz retorna um vetor linha com a soma de cada coluna.
std(A) : se A é um vetor, retorna o desvio-padrão dos elementos do vetor.
det(A) : retorna o determinante da matriz quadrada A.
dot(a,b) : determina o produto escalar de dois vetores a e b.
cross(a,b) : determina o produto vetorial de dois vetores a e b. Os dois vetores
devem possuir três elementos.
Centro Educacional Uninorte 47](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-47-320.jpg)

![Gráficos - Exemplo 1
>> plot ([1, 2, 3], [4, 3, 6], [1, 2, 3], [5, 7, 6])
Dois gráficos em uma só figura
(gerados pelo código acima)
Um gráfico é gerado pelo par de
vetores [1, 2, 3], [4, 3, 6] e
outro pelo par [1, 2, 3], [5,
7, 6]
Centro Educacional Uninorte 49](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-49-320.jpg)

![Outros comandos auxiliares para gráficos
legend( textol', 'texto2', location', pos ) : Coloca as legendas na posição
indicada por "pos", que podem ser: north, south, east, weast, northeast, northwest,
southeast, Southwest.
grid on : Adiciona grades no gráfico plotado;
grid off : Retira as grades do gráfico corrente:
hold on e hold off : Usa-se para plotar outro gráfico na mesma figura. Este
comando mantém o gráfico antigo até que o hold off seja usado. Assim, consegue-
se sobrepor os gráficos.
axis(v) : Este comando é utilizado para representar o gráfico em uma
determinada faixa de valores determinada pelo vetor v . O vetor tem como
elementos os valores mínimo e máximo dos eixos x e y ([xmin xmax ymin ymax]).
Centro Educacional Uninorte 51](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-51-320.jpg)





![Funções Especiais de Plotagem em 2 Dimensões
bar(x,y) , Dados 2 vetores de dados x e y, é produzido um gráfico de
barras. Se somente um argumento é dado, pegamos os valores de y, e as
coordenadas x são colocadas para ser o índice dos elementos.
´ equivalente a: [xb,yb] = bar(x,y); plot(xb,yb) ;
loglog(args) , Plota em escala logarítmica ambos os eixos.
polar(θ, ρ) , Faz um gráfico de acordo com as coordenadas polares θ e ρ.
semilogy(args) , Gráfico logarítmico somente no eixo y.
semilogx(args) , Gráfico logarítmico somente no eixo x.
stairs(x, y) , Gráfico em degrau.
loglog(args) , Plota em escala logarítmica ambos os eixos.
Centro Educacional Uninorte 58](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-58-320.jpg)

![Plotando em 3
dimensões
Exemplo:
>> [x,y]=meshgrid(-4:0.6:4,-3:0.6:3);
>> z=x.^2+y.^2;
>> grid;
>> xlabel('eixo x');
>> ylabel('eixo y');
>> zlabel('eixo z');
>> title('Exemplo de Mesh');
>> mesh(x,y,z);
Centro Educacional Uninorte 60](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-60-320.jpg)







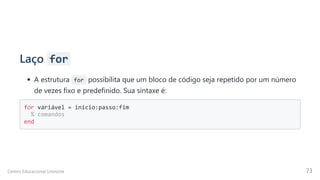
![Exemplo for
N = input('Digite um número natural: ');
disp(' ')
disp('Método 1 - Laço FOR')
disp(' ')
soma = 0;
tic;
for n = 1:N
soma = soma + n;
end
disp(['A soma de 1 até ' num2str(N) ' é ' num2str(soma)]);
toc;
Centro Educacional Uninorte 74](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-74-320.jpg)
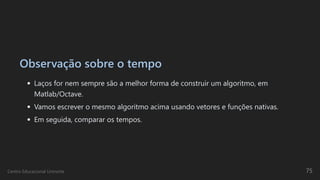
![Soma - funções nativas
disp(' ')
disp('Método 2 - vetores e funções nativas')
disp(' ')
tic;
t = [1:N];
soma2 = sum(t);
disp(['A soma de 1 até ' num2str(N) ' é ' num2str(soma)]);
toc;
Centro Educacional Uninorte 76](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-76-320.jpg)


![Exemplo while 1
1. Encontre o menor número
x=1;
n=0;
while x>1e-12
n = n+1;
x = x/2;
end
disp(['Quando n = ' num2str(n) ', a sequência 1/(2^n) chegou a ' num2str(x)]);
>> menor_numero_n
Quando n = 40, a sequência 1/(2^n) chegou a 9.0949e-13
n ∈ N ∪ {0} tal que <
2n
1
10 12
−
Centro Educacional Uninorte 79](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-79-320.jpg)
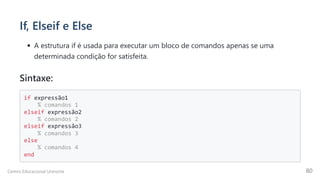
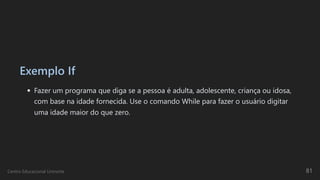
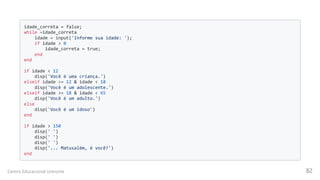
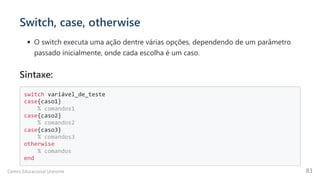

![n = input('Digite um número: '); m = input('Digite um número: ');
operacao = input('Digite: 1 para somá-los; 2 para subtraí-los; 3 para multiplicá-los. Opção: ');
switch operacao
case{1}
oper='+';
x=n+m;
case{2}
oper='-';
x=n-m;
case{3}
oper='*';
x=m*n;
otherwise
x=NaN;
disp('Essa não é uma operação válida')
end
if x ~= NaN
disp([num2str(n) oper num2str(m) '=' num2str(x)])
end
Centro Educacional Uninorte 85](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-85-320.jpg)
![Funções
Muitas vezes queremos criar funções que ainda não estão na biblioteca virtual do
Octave/MATLAB. Para isso temos o comando function , que obedece a seguinte
sintaxe:
function[saida] = nomedafuncao(entrada)
% Comentário da função, que aparecerá quando fizer '>>> help nomedafuncao'
<comandos>
end
Centro Educacional Uninorte 86](https://image.slidesharecdn.com/cartilhadeoctaveparamatematicacomputacional-220706164303-bac8faac/85/Cartilha-de-Octave-para-Matematica-Computacional-pdf-86-320.jpg)
