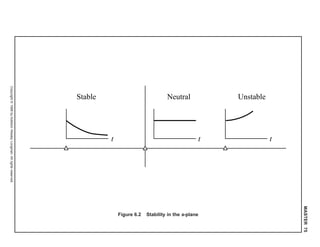
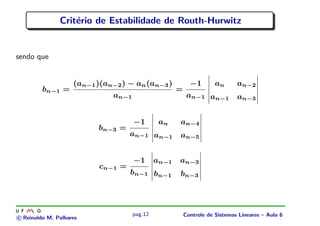
[1] O documento discute conceitos de estabilidade de sistemas lineares realimentados e o critério de Routh-Hurwitz para verificar a estabilidade desses sistemas.
[2] O critério de Routh-Hurwitz analisa os sinais dos elementos da primeira coluna de um arranjo formado pelos coeficientes do polinômio característico do sistema.
[3] Se todos os elementos tiverem o mesmo sinal, o sistema é estável, pois não haverá raízes com parte real positiva que tornariam o sistema instável.