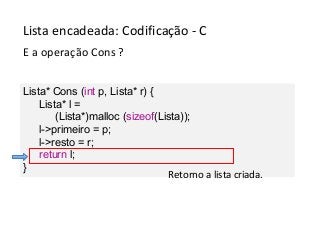
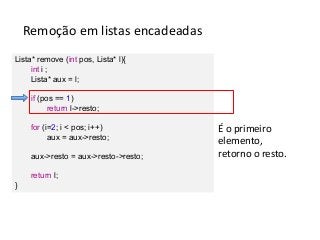
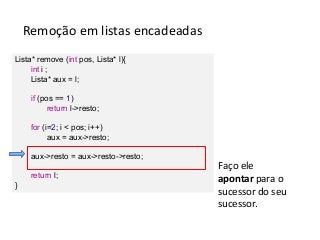
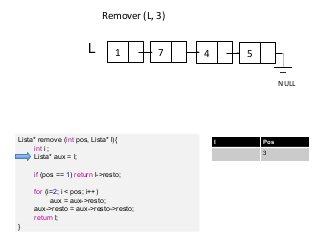
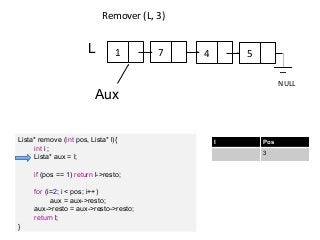
Este documento apresenta um resumo sobre listas encadeadas. As principais ideias apresentadas são: 1) Listas encadeadas são uma estrutura de dados recursiva na qual os elementos são ligados uns aos outros através de ponteiros, permitindo adicionar elementos dinamicamente sem preocupar com o tamanho da memória; 2) As operações sobre listas encadeadas geralmente são implementadas de forma recursiva, tratando casos triviais e reduzindo o problema a subproblemas menores; 3) Exemplos de operações comuns como tamanho, busca e inserção

1. Listas Encadeadas
Prof: Sergio Souza Costa

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
http://www.slideshare.net/skosta/presentations?order=popular
https://twitter.com/profsergiocosta
http://gplus.to/sergiosouzacosta

3. Roteiro
• Lista como estrutura encadeada.
• Codificação de listas encadeadas em C.

4. Como representar as listas na
memoria do computador?
Estruturas contíguas
Estruturas Encadeadas

5. Estruturas encadeadas
Nas estruturas contíguas a relação de ordem dos elementos é
estabelecida de forma física, a posição x2 sucede a posição de
x1 .
Nas estruturas encadeadas a sucessão dos elementos é
estabelecida de forma lógica, a posição x2 não
necessariamente sucede a de x1.
Não existe uma relação espacial (memória).
Deste modo, pode-se adicionar elementos dinamicamente,
mantendo a relação de ordem sem se preocupar de definir
o tamanho máximo de memoria.

6. Estruturas encadeadas
Uma lista pode ser implementada usando a estrutura
de dados listas encadeadas.

7. Estruturas encadeadas
Uma lista pode ser implementada usando a estrutura
de dados listas encadeadas.
Observem: listas encadeadas é uma outra estrutura de
dados, com suas propriedades, tipo abstrato de dados
e implementação.

8. Estruturas encadeadas
Começando por uma definição abstrata
sobre listas encadeadas ...

9. Estruturas encadeadas
Começando por uma definição abstrata
sobre listas encadeadas ...

10. Listas encadeadas
Uma lista encadeada é uma estrutura recursiva, ou
seja, definida em termos de si mesma.
Aqui definimos uma lista encadeada como:
• Uma sequência de 0 ou mais itens (ou elementos),
onde o seu tamanho e sua quantidade de itens.
• Uma lista encadeada vazia possui 0 itens e será
representada por [].

11. Listas encadeadas
Uma lista encadeada não vazia L consiste de dois atributos:
1.
2.
Primeiro[L] que é o primeiro item da lista e
Resto[L] que são os demais itens, ou seja, uma lista
contendo todos os itens com exceção do primeiro.
• Se uma lista L contem apenas um elemento, então
Resto[L] é uma lista vazia [].
• Deste modo, tudo que se aplica a lista L também se
aplica a Resto[L].

12. Listas encadeadas
Como uma lista pode ser vazia ou conter pelo menos um
item, ela requer dois construtores:
VAZIA(): cria uma lista vazia.
CONS(x, L): cria uma lista não vazia composta pelo
primeiro elemento x e um resto L.
Pode se dizer ainda que o construtor CONS
insere um item x a uma lista L.

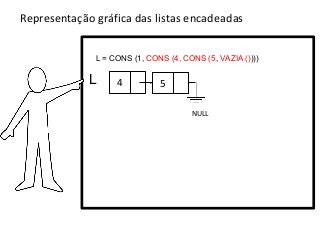
13. LISTA encadeada - Operação "cons"
Exemplos:
A variável lista1 equivale a seguinte lista [1,4,5]:
>lista1 = CONS (1, CONS (4, CONS (5, VAZIA ())))
A variável lista2 equivale a seguinte lista [9,2,3]:
>lista2 = CONS (9, CONS (2, CONS (3, VAZIA ())))

14. Listas encadeadas
>lista1 = CONS (1, CONS (4, CONS (5, VAZIA ())))

15. Listas encadeadas
>lista1 = CONS (1, CONS (4, CONS (5, VAZIA ())))
= []

16. Listas encadeadas
>lista1 = CONS (1, CONS (4, CONS (5, VAZIA ())))
= []
= [5]

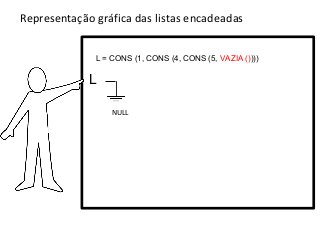
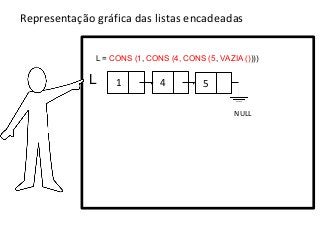
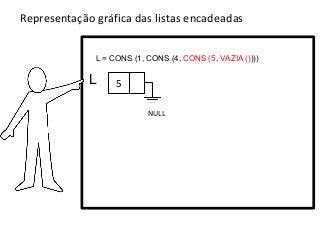
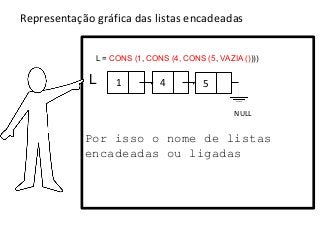
17. Listas encadeadas
>lista1 = CONS (1, CONS (4, CONS (5, VAZIA ())))
= []
= [5]
= [4,5]

18. Listas encadeadas
>lista1 = CONS (1, CONS (4, CONS (5, VAZIA ())))
= []
= [5]
= [4,5]
= [1,4,5]

19. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
c = Resto [Resto [A]]
d = Primeiro [A]
e = Primeiro [Resto[A]]
f = Resto [Primeiro[a]]

20. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
c = Resto [Resto [A]]
d = Primeiro [A]
e = Primeiro [Resto[A]]
f = Resto [Primeiro[a]]
[5,7,8]

21. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
[7,8]
c = Resto [Resto [A]]
d = Primeiro [A]
e = Primeiro [Resto[A]]
f = Resto [Primeiro[a]]
[5,7,8]

22. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
[7,8]
c = Resto [Resto [A]]
d = Primeiro [A]
e = Primeiro [Resto[A]]
f = Resto [Primeiro[a]]
[8]
[5,7,8]

23. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
[7,8]
[8]
c = Resto [Resto [A]]
d = Primeiro [A]
5
e = Primeiro [Resto[A]]
f = Resto [Primeiro[a]]
[5,7,8]

24. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
[7,8]
[8]
c = Resto [Resto [A]]
d = Primeiro [A]
5
e = Primeiro [Resto[A]]
f = Resto [Primeiro[a]]
7
[5,7,8]

25. Exercitando
Quais os valores das variáveis abaixo:
A = Cons (5, Cons (7, Cons (8, Vazia() ) ) )
B = Resto [A]
[7,8]
[8]
c = Resto [Resto [A]]
d = Primeiro [A]
5
e = Primeiro [Resto[A]]
7
f = Resto [Primeiro[a]]
inválida
[5,7,8]

26. LISTA: Tipo de dados abstrato
Lembrando as 5 operações básicas de lista.
Operação
Descrição
Tamanho (L)
Retorna o número de elementos de L
Inserir (L,x)
Insere um elemento x a L
Busca (L, x)
Busca um elemento x em L, retorna seu indice.
ElementoEm(L, i)
Retorna um elemento de L localizado em i.
Remove (L, i)
Remove um elemento de L localizado em i.

27. Listas encadeadas e funções recursivas
Como a lista encadeada é uma estrutura recursiva, as
operações sobre estas são usualmente desta forma.
Lembrando .......
Uma função recursiva consiste em duas partes:
• O caso trivial, cuja solução é conhecida;
• Um método geral que reduz o problema a um ou mais
problemas menores (subproblemas) de mesma
natureza.

28. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Tamanho (L)

29. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.

30. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.

31. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.
Pela definição o tamanho de
uma lista vazia é 0.

32. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
retorna 0
se não
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.
Pela definição o tamanho de
uma lista vazia é 0.

33. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
retorna 0
se não
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.
Pela definição o tamanho de
uma lista vazia é 0.
Se e não vazia, ela tem pelo menos um
elemento, adicionado ao tamanho do
resto da lista

34. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
retorna 0
se não
retorna 1 + Tamanho (Resto[L])
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.
Pela definição o tamanho de
uma lista vazia é 0.
Se e não vazia, ela tem pelo menos um
elemento, adicionado ao tamanho do
resto da lista

35. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
retorna 0
se não
retorna 1 + Tamanho (Resto[L])
Caso trivial
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.
Pela definição o tamanho de
uma lista vazia é 0.
Se e não vazia, ela tem pelo menos um
elemento, adicionado ao tamanho do
resto da lista

36. Operações: tamanho
Por exemplo, a operação Tamanho retorna a quantidade de
itens em uma lista:
Pela definição uma lista pode ser
Tamanho (L)
Se L = VAZIA() então
retorna 0
se não
retorna 1 + Tamanho (Resto[L])
Caso trivial
Método geral
vazia, ou conter pelo menos um
elemento. Então precisamos tratar
estes dois casos.
Pela definição o tamanho de
uma lista vazia é 0.
Se e não vazia, ela tem pelo menos um
elemento, adicionado ao tamanho do
resto da lista

37. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]

38. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]
= 1 + Tamanho [5,7,8]

39. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]
= 1 + Tamanho [5,7,8]
= 1 + 1 + Tamanho [7,8]

40. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]
= 1 + Tamanho [5,7,8]
= 1 + 1 + Tamanho [7,8]
= 1 + 1 + 1 + Tamanho [8]

41. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]
= 1 + Tamanho [5,7,8]
= 1 + 1 + Tamanho [7,8]
= 1 + 1 + 1 + Tamanho [8]
= 1 +1 + 1 + 1 + Tamanho []

42. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]
= 1 + Tamanho [5,7,8]
= 1 + 1 + Tamanho [7,8]
= 1 + 1 + 1 + Tamanho [8]
= 1 +1 + 1 + 1 + Tamanho []
= 1 +1 + 1 + 1 + 0

43. Operações: tamanho
A simulação da avaliação desta função recursiva
é mostrada a seguir:
Tamanho [3,5,7,8]
= 1 + Tamanho [5,7,8]
= 1 + 1 + Tamanho [7,8]
= 1 + 1 + 1 + Tamanho [8]
= 1 +1 + 1 + 1 + Tamanho []
= 1 +1 + 1 + 1 + 0
=4

44. Operações: Inserção
Inserir no inicio, basta retornar a chamada a
função CONS.
L = [ 6,7,5,4]
Inserir( L, x)
1. retorna CONS (x, L)
Inserir (L, 2)
L = [ 2, 6,7,5,4]

45. Operações: Inserção
Inserir no inicio, basta retornar a chamada a
função CONS.
L = [ 6,7,5,4]
Inserir( L, x)
1. retorna CONS (x, L)
Inserir (L, 2)
L = [ 2, 6,7,5,4]
Depois falaremos sobre inserção no fim da lista.

46. Operações: Busca
Buscar um elemento x em L.
Busca(L, x)

47. Operações: Busca
Buscar um elemento x em L.
Busca(L, x)
Se L = VAZIA() então
senao
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:

48. Operações: Busca
Buscar um elemento x em L.
Busca(L, x)
Se L = VAZIA() então
senao
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:
Se L é vazia, então sabemos que X não
está em L. É o caso trivial.

49. Operações: Busca
Buscar um elemento x em L.
Busca(L, x)
Se L = VAZIA() então
retorna NULL;
senao
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:
Se L é vazia, então sabemos que X não
está em L. É o caso trivial.

50. Operações: Busca
Buscar um elemento x em L.
Busca(L, x)
Se L = VAZIA() então
retorna NULL;
senao
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:
Se L é vazia, então sabemos que X não
está em L. É o caso trivial.
Caso contrário, precisamos verificar se
x é o primeiro, ou se ele está
localizado no restante da lista.

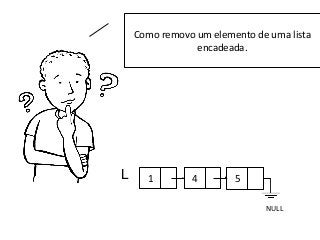
51. Operações: Busca
Buscar um elemento x em L.
Busca(L, x)
Se L = VAZIA() então
retorna NULL;
senao
Se Primeiro[L] = x entao
retorna L
senao
retorna Busca (resto[L],x)
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:
Se L é vazia, então sabemos que X não
está em L. É o caso trivial.
Caso contrário, precisamos verificar se
x é o primeiro, ou se ele está
localizado no restante da lista.

52. Operações: ElementoEm
Neste caso, não existe um índice, é necessário
percorrer a lista até chegar na posição desejada.
ElementoEm( L, i)
Se L = Vazia entao
senao
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:

53. Operações: ElementoEm
Neste caso, não existe um índice, é necessário
percorrer a lista até chegar na posição desejada.
ElementoEm( L, i)
Se L = Vazia entao
erro (“lista vazia”)
senao
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:
Lista vazia, é um erro

54. Operações: ElementoEm
Neste caso, não existe um índice, é necessário
percorrer a lista até chegar na posição desejada.
ElementoEm( L, i)
Se L = Vazia entao
erro (“lista vazia”)
senao
Se i = 1 entao
retorna Primeiro[L]
senao
retorna
ElementoEm(Resto[L], i-1))
Como sempre, preciso tratar os
casos quando a lista é vazia e
quando não é:
Lista vazia, é um erro
Caso contrário, se o indice for 1,
entao retorne o primeiro, caso
contrario retorne o ElementoEm
(resto[L], indice -1)

55. Operações: ElementoEm
Simulação
ElementoEm ([5,6,7,8], 3)
ElementoEm( L, i)
Se L = Vazia entao
erro (“lista vazia”)
senao
Se i = 1 entao
retorna Primeiro[L]
senao
retorna
ElementoEm(Resto[L], i-1))

56. Operações: ElementoEm
Simulação
ElementoEm ([5,6,7,8], 3)
= ElementoEm ([6,7,8],2)
ElementoEm( L, i)
Se L = Vazia entao
erro (“lista vazia”)
senao
Se i = 1 entao
retorna Primeiro[L]
senao
retorna
ElementoEm(Resto[L], i-1))

57. Operações: ElementoEm
Simulação
ElementoEm ([5,6,7,8], 3)
= ElementoEm ([6,7,8],2)
= ElementoEm ([7,8],1)
ElementoEm( L, i)
Se L = Vazia entao
erro (“lista vazia”)
senao
Se i = 1 entao
retorna Primeiro[L]
senao
retorna
ElementoEm(Resto[L], i-1))

58. Operações: ElementoEm
Simulação
ElementoEm ([5,6,7,8], 3)
= ElementoEm ([6,7,8],2)
= ElementoEm ([7,8],1)
=7
ElementoEm( L, i)
Se L = Vazia entao
erro (“lista vazia”)
senao
Se i = 1 entao
retorna Primeiro[L]
senao
retorna
ElementoEm(Resto[L], i-1))

59. Atividade
Considerando apenas as 4 operações (Cons, Vazia, Primeiro, Resto) ,
podemos codificar diversas outras funções. No papel, codifiquem as
funções abaixo (versão iterativa e recursiva):
a) int soma (List l )
ex: soma [1,2,6] → 9
b) int produto (List l )
ex: produto [1,2,6] -> 12
c) void imprimir (List a)
ex: imprimir ([1,2]) → [1,2]
d) List concatena (List l1,List l2)
ex: concatena ([1,2],[3,4]) → [1,2,3,4]

60. Entendi o TAD da lista, mas está muito
abstrato. Como escrevo isso em uma
linguagem de programação.

61. Entendi o TAD da lista, mas está muito
abstrato. Como escrevo isso em uma
linguagem de programação.
Ponto crucial: como as linguagens suportam
tipos de dados recursivos. Alguém?

62. Entendi o TAD da lista, mas está muito
abstrato. Como escrevo isso em uma
linguagem de programação.
Ponto crucial: como as linguagens suportam
tipos de dados recursivos. Alguém?
Vocês já usaram.

63. Entendi o TAD da lista, mas está muito
abstrato. Como escrevo isso em uma
linguagem de programação.
Ponto crucial: como as linguagens suportam
tipos de dados recursivos. Alguém?
Vocês já usaram.
Ponteiros

64. Lista encadeada: Codificação - C
Como criamos novos tipos de dados em C ?

65. Lista encadeada: Codificação - C
Como criamos novos tipos de dados em C ?
typedef struct Lista {
} Lista;
Esta é a sintaxe básica
para criar qualquer tipo
de dado, mas quais
eram os atributos de
uma lista não vazia ?

66. Lista encadeada: Codificação - C
Como criamos novos tipos de dados em C ?
typedef struct Lista {
int primeiro;
} Lista;
Primeiro, que retorna o
primeiro valor da lista.
Neste caso assumindo
uma lista homogênea
de inteiros.

67. Lista encadeada: Codificação - C
Como criamos novos tipos de dados em C ?
typedef struct Lista {
int primeiro;
struct Lista* resto;
} Lista;
Resto, os elementos
de uma lista com
excessão do primeiro.
Neste, caso é do tipo
lista.

68. Lista encadeada: Codificação - C
Como criamos novos tipos de dados em C ?
typedef struct Lista {
int primeiro;
struct Lista* resto;
} Lista;
Observem a recursividade.
Resto, os elementos
de uma lista com
excessão do primeiro.
Neste, caso é do tipo
lista.

69. Ok, mas esta é uma lista não vazia, e uma lista
vazia, como represento ?
Como estamos trabalhando com ponteiros,
representamos uma lista vazia por um
ponteiro nulo, ou seja, pelo NULL em C.

70. Lista encadeada: Codificação - C
Como iremos codificar a operação que cria uma
lista vazia ?
Lista* Vazia () {

71. Lista encadeada: Codificação - C
Como iremos codificar a operação que cria uma
lista vazia ?
Lista* Vazia () {
return NULL;
}

72. Lista encadeada: Codificação - C
E a operação Cons ?
Lista* Cons (int p, Lista* r) {
Lista* l =
(Lista*)malloc (sizeof(Lista));
l->primeiro = p;
l->resto = r;
return l;
}

73. Lista encadeada: Codificação - C
E a operação Cons ?
Lista* Cons (int p, Lista* r) {
Lista* l =
(Lista*)malloc (sizeof(Lista));
l->primeiro = p;
l->resto = r;
return l;
}
É alocado a área de memoria
para a lista.

74. Lista encadeada: Codificação - C
E a operação Cons ?
Lista* Cons (int p, Lista* r) {
Lista* l =
(Lista*)malloc (sizeof(Lista));
l->primeiro = p;
l->resto = r;
return l;
}
Atribuo os valores dos
parâmetros para os atributos
da lista.

75. Lista encadeada: Codificação - C
E a operação Cons ?
Lista* Cons (int p, Lista* r) {
Lista* l =
(Lista*)malloc (sizeof(Lista));
l->primeiro = p;
l->resto = r;
return l;
}
Retorno a lista criada.

76. L = CONS (1, CONS (4, CONS (5, VAZIA ())))
L

77. Representação gráfica das listas encadeadas
L = CONS (1, CONS (4, CONS (5, VAZIA ())))
L
NULL

78. Representação gráfica das listas encadeadas
L = CONS (1, CONS (4, CONS (5, VAZIA ())))
L
5
NULL

79. Representação gráfica das listas encadeadas
L = CONS (1, CONS (4, CONS (5, VAZIA ())))
L
4
5
NULL

80. Representação gráfica das listas encadeadas
L = CONS (1, CONS (4, CONS (5, VAZIA ())))
L
1
4
5
NULL

81. Representação gráfica das listas encadeadas
L = CONS (1, CONS (4, CONS (5, VAZIA ())))
L
1
4
5
NULL
Por isso o nome de listas
encadeadas ou ligadas

82. Como removo um elemento de uma lista
encadeada.

83. Como removo um elemento de uma lista
encadeada.
L
1
4
5
NULL

84. Supondo que eu queira remover o primeiro
elemento ....
L
1
4
5
NULL

85. Supondo que eu queira remover o primeiro
elemento ....
Basta retornar o resto da lista, ou seja, a
partir do segundo.
L
4
5
NULL

86. Supondo que eu queira remover o
segundo elemento ....
L
1
4
5
NULL

87. Supondo que eu queira remover o segundo
elemento ....
Basta fazer o primeiro apontar para o
terceiro ...
L
1
4
5
NULL

88. Remoção em listas encadeadas
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1)
return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}

89. Remoção em listas encadeadas
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1)
return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
É o primeiro
elemento,
retorno o resto.

90. Remoção em listas encadeadas
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1)
return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
Caso contrário,
percorro a lista
até pos-1.

91. Remoção em listas encadeadas
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1)
return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
Faço ele
apontar para o
sucessor do seu
sucessor.

92. Remover (L, 3)
L
1
7
4
5
NULL
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
3

93. Remover (L, 3)
L
1
7
4
5
NULL
Aux
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
3

94. Remover (L, 3)
L
1
7
4
5
NULL
Aux
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
3

95. Remover (L, 3)
L
1
7
4
5
NULL
Aux
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
2
3

96. Remover (L, 3)
L
1
7
4
5
NULL
Aux
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
2
3

97. Remover (L, 3)
L
1
7
4
5
NULL
Aux
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
3
3

98. Remover (L, 3)
L
1
7
4
5
NULL
Aux
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
I
Pos
3
3

99. Remover (L, 3)
L
1
O que irá acontece com o
espaço de memoria onde
está localizado o 4?
Lista* remove (int pos, Lista* l){
int i ;
Lista* aux = l;
if (pos == 1) return l->resto;
for (i=2; i < pos; i++)
aux = aux->resto;
aux->resto = aux->resto->resto;
return l;
}
7
4
5
NULL
Aux
I
Pos
3
3

100. Pontos chaves
• Nas estruturas encadeadas os itens são
adicionados dinamicamente.
• Listas encadeadas são estruturas recursivas e
suportadas por ponteiros em C.

101. Referências
• CORMEN, Thomas H. et al. Algoritmos: teoria
e prática. Rio de Janeiro: Elsevier, 2002.
• SILVA, Osmar Quirino da. Estrutura de dados e
algoritmos usando C: fundamentos e
aplicações. Rio de Janeiro:Ciência Moderna,
2007. 458 p. ISBN 9788573936117
• CELES, Waldemar; CERQUEIRA, Renato;
RANGEL, José Lucas. Introdução a estruturas
de dados. Editora Campus, 2004.