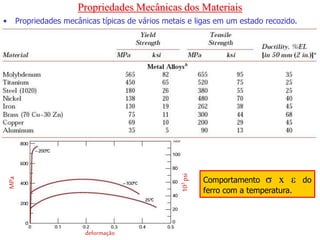
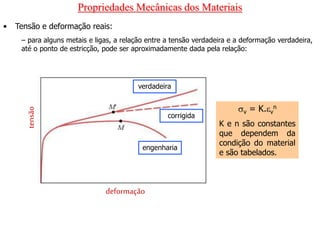
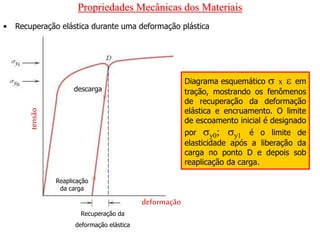
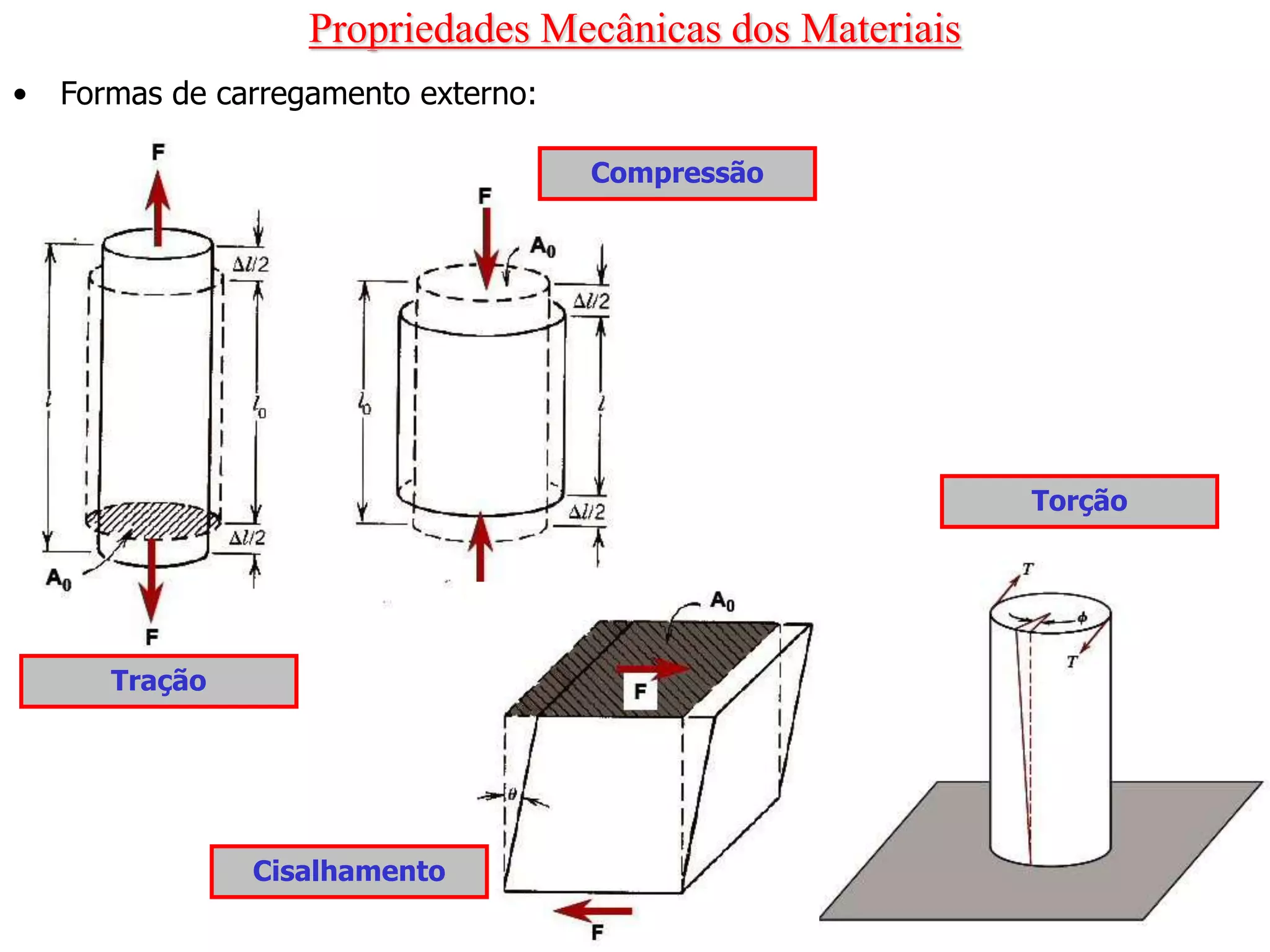
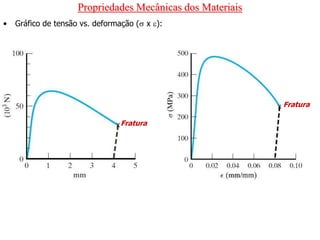
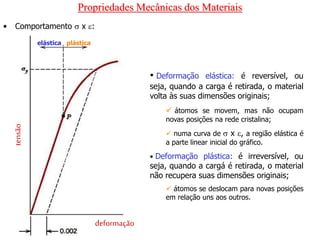
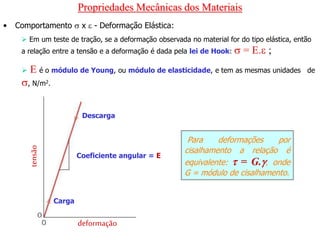
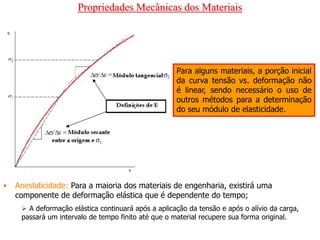
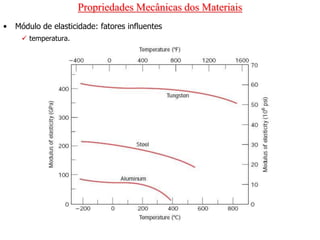
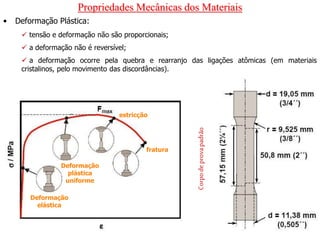
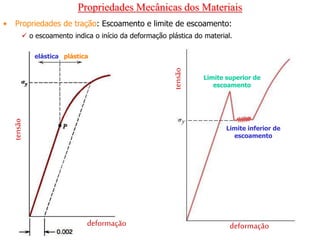
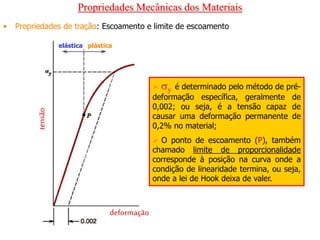
O documento discute as propriedades mecânicas dos materiais, incluindo formas de carregamento externo, testes de tração, comportamento tensão-deformação, propriedades elásticas e plásticas, e como essas propriedades variam entre diferentes materiais.
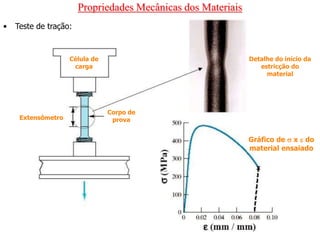
![Propriedades Mecânicas dos Materiais
• Propriedades de tração: Ductilidade
é o grau de deformação plástica suportado até a fratura do material;
pode ser medida pelo alongamento percentual ou pela redução de área percentual.
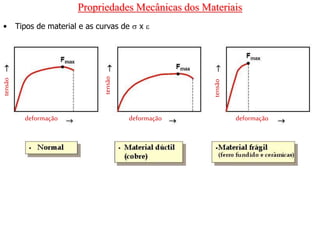
tensão
deformação
frágil
dúctil
Alongamento percentual:
AL % = [(lf – l0)/l0]/x100
Redução de área percentual
RA % = [(A0 – Af)/A0]/x100](https://image.slidesharecdn.com/aula1-211110011631/85/Aula1-15-320.jpg)