6 propriedades mecanicas (1)

1
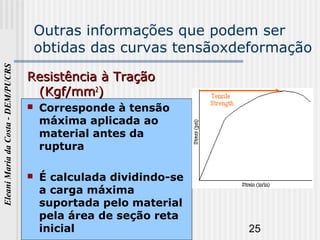
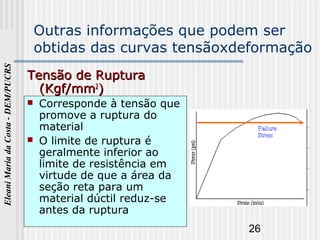
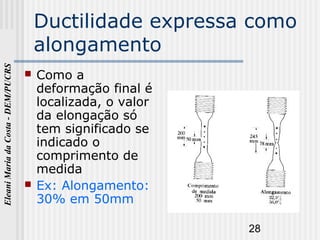
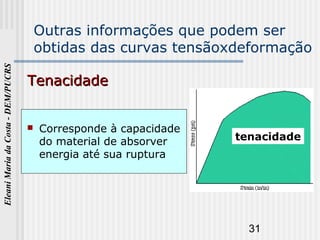
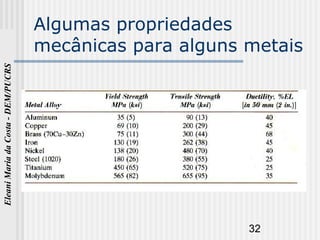
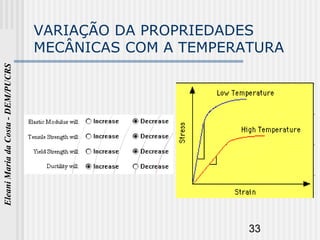
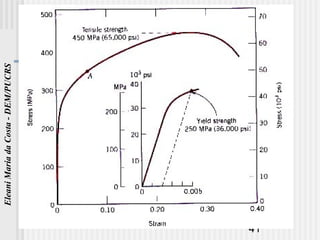
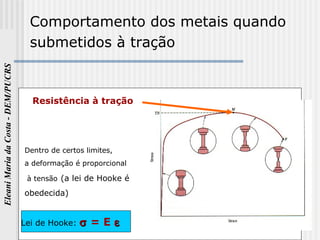
6-PROPRIEDADES
MECÂNICAS DOS METAIS

2
EleaniMariadaCosta-DEM/PUCRS
PROPRIEDADES
MECÂNICAS
POR QUÊ ESTUDAR?
 A determinação e/ou conhecimento das
propriedades mecânicas é muito importante
para a escolha do material para uma
determinada aplicação, bem como para o projeto
e fabricação do componente.
 As propriedades mecânicas definem o
comportamento do material quando sujeitos à
esforços mecânicos, pois estas estão
relacionadas à capacidade do material de resistir
ou transmitir estes esforços aplicados sem
romper e sem se deformar de forma
incontrolável.

3
Principais propriedades
mecânicas
 Resistência à tração
 Elasticidade
 Ductilidade
 Fluência
 Fadiga
 Dureza
 Tenacidade,....
Cada uma dessas propriedades está associada à habilidade
do material de resistir às forças mecânicas e/ou de
transmiti-las

4
TIPOS DE TENSÕES QUE UMA
ESTRUTURA ESTA SUJEITA
 Tração
 Compressão
 Cisalhamento
 Torção

5
Como determinar as
propriedades mecânicas?
 A determinação das propriedades mecânicas é
feita através de ensaios mecânicos.
 Utiliza-se normalmente corpos de prova
(amostra representativa do material) para o
ensaio mecânico, já que por razões técnicas e
econômicas não é praticável realizar o ensaio na
própria peça, que seria o ideal.
 Geralmente, usa-se normas técnicas para o
procedimento das medidas e confecção do corpo
de prova para garantir que os resultados sejam
comparáveis.

6
NORMAS TÉCNICAS
As normas técnicas mais comuns são
elaboradas pelas:
 ASTM (American Society for Testing and
Materials)
 ABNT (Associação Brasileira de
Normas Técnicas)

7
TESTES MAIS COMUNS PARA SE
DETERMINAR AS PROPRIEDADES
MECÂNICAS DOS METAIS
 Resistência à tração (+ comum,
determina a elongação)
 Resistência à compressão
 Resistência à torção
 Resistência ao choque
 Resistência ao desgaste
 Resistência à fadiga
 Dureza
 Etc...

8
RESISTÊNCIA À TRAÇÃO
É medida submetendo-se o material à
uma carga ou força de tração,
paulatinamente crescente, que
promove uma deformação progressiva
de aumento de comprimento
NBR-6152 para metais

9
ESQUEMA DE MÁQUINA
PARA ENSAIO DE TRAÇÃO
PARTES BÁSICAS
 Sistema de aplicação de carga
 dispositivo para prender o corpo de prova
 Sensores que permitam medir a tensão
aplicada e a deformação promovida
(extensiômetro)

10
RESITÊNCIA À TRAÇÃO
TENSÃO (σ) X Deformação (ε)
σ = F/Ao Kgf/cm2
ou Kgf/mm2
ou N/ mm2
Como efeito da aplicação de uma tensão tem-se a
deformação (variação dimensional).
A deformação pode ser
expressa:
•O número de milímetrosa de deformação
por milímetros de comprimento
• O comprimento deformado como uma
percentagem do comprimento original
Deformação(εε))= lf-lo/lo= ∆l/lo
lo= comprimento inicial
lf= comprimento final
Força ou carga
Área inicial da seção reta transversal

11
Comportamento dos metais quando
submetidos à tração
Resistência à tração
Dentro de certos limites,
a deformação é proporcional
à tensão (a lei de Hooke é
obedecida)
Lei de Hooke: σσ = E εε

12
A deformação pode ser:
 Elástica
 Plástica

13
Deformação Elástica e Plástica
DEFORMAÇÃO ELÁSTICA
 Prescede à deformação
plástica
 É reversível
 Desaparece quando a tensão é
removida
 É praticamente proporcional à
tensão aplicada (obedece a lei
de Hooke)
DEFORMAÇÃO PLÁSTICA
 É provocada por tensões que
ultrapassam o limite de elasticidade
 É irreversível porque é resultado do
deslocamento permanente dos
átomos e portanto não desaparece
quando a tensão é removida
Elástica Plástica

14
Módulo de elasticidade ouMódulo de elasticidade ou
Módulo de YoungMódulo de Young
E= σσ// εε =Kgf/mm=Kgf/mm22
• É o quociente entre a tensão
aplicada e a deformação
elástica resultante.
•Está relacionado com a rigidez
do material ou à resist. à
deformação elástica
•Está relacionado
diretamente com as forças
das ligações interatômicas
Lei de Hooke: σσ = E εε
P A lei de Hooke só é
válida até este ponto
Tg α= E
α

15
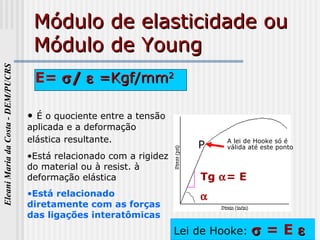
Módulo de Elasticidade para
alguns metais
Quanto maior o módulo de elasticidade mais rígido é oQuanto maior o módulo de elasticidade mais rígido é o
material ou menor é a sua deformação elástica quandomaterial ou menor é a sua deformação elástica quando
aplicada uma dada tensãoaplicada uma dada tensão
MÓDULO DE ELASTICIDADE
[E]
GPa 106
Psi
Magnésio 45 6.5
AlumÍnio 69 10
Latão 97 14
Titânio 107 15.5
Cobre 110 16
Níquel 207 30
Aço 207 30
Tungstênio 407 59

16
Comportamento não-linear
 Alguns metais como
ferro fundido
cinzento, concreto e
muitos polímeros
apresentam um
comportamento não
linear na parte
elástica da curva
tensão x
deformação

17
Considerações gerais sobre
módulo de elasticidade
Como consequência do módulo de
elasticidade estar diretamente
relacionado com as forças interatômicas:
 Os materiais cerâmicos tem alto módulo
de elasticidade, enquanto os materiais
poliméricos tem baixo
 Com o aumento da temperatura o módulo
de elasticidade diminui
* Considerando o mesmo material sendo este
monocristalino, o módulo de elasticidade depende
apenas da orientação cristalina

18
O COEFICIENTE DE POISSON PARA
ELONGAÇÃO OU COMPRESSÃO
• Qualquer
elongação ou
compressão de
uma estrutura
cristalina em
uma direção,
causada por
uma força
uniaxial, produz
um ajustamento
nas dimensões
perpendiculares
à direção da
força
x
z

19
O COEFICIENTE DE POISSON PARA
TENSÕES DE CISALHAMENTO
• Tensões de
cisalhamento
produzem
deslocamento
de um plano de
átomos em
relação ao plano
adjacente
•A deformação
elástica de
cisalhamento é
dada (γ ):
γ= tgα
Módulo de
Cisalhamento ou de
rigidez

20
Forças de compressão,
cisalhamento e torção
 O comportamento elástico também
é observado quando forças
compressivas, tensões de
cisalhamento ou de torção são
impostas ao material

21
O FENÔMENO DE
ESCOAMENTO
 Esse fenômeno é nitidamente
observado em alguns metais de
natureza dúctil, como aços baixo
teor de carbono.
 Caracteriza-se por um grande
alongamento sem acréscimo de
carga.

22
Outras informações que podem ser
obtidas das curvas tensãoxdeformação
Tensão de escoamentoTensão de escoamento
σy= tensão de escoamento
(corresponde a tensão máxima
relacionada com o fenômeno de
escoamento)
• De acordo com a curva “a”, onde não
observa-se nitidamente o fenômeno de
escoamento
•Alguns aços e outros materiais exibem o
comportamento da curva “b”, ou seja, o limite
de escoamento é bem definido (o material
escoa- deforma-se plasticamente-sem
praticamente aumento da tensão). Neste caso,
geralmente a tensão de escoamento
corresponde à tensão máxima verificada
durante a fase de escoamento
Não ocorre escoamento
propriamente dito
Escoamento

23
Limite de Escoamento
quando não observa-se
nitidamente o fenômeno
de escoamento, a tensão de
escoamento corresponde
à tensão necessária para promover
uma deformação permanente de
0,2% ou outro valor especificado
(obtido pelo método gráfico
indicado na fig. Ao lado)
Fonte figura: Prof. Sidnei Paciornik do Departamento de Ciência dos Materiais
e Metalurgia da PUC-Rio

24

25
Resistência à TraçãoResistência à Tração
(Kgf/mm(Kgf/mm22
))
 Corresponde à tensão
máxima aplicada ao
material antes da
ruptura
 É calculada dividindo-se
a carga máxima
suportada pelo material
pela área de seção reta
inicial

26
Tensão de RupturaTensão de Ruptura
(Kgf/mm(Kgf/mm22
))
 Corresponde à tensão que
promove a ruptura do
material
 O limite de ruptura é
geralmente inferior ao
limite de resistência em
virtude de que a área da
seção reta para um
material dúctil reduz-se
antes da ruptura

27
Corresponde ao
alongamento total do
material devido à
deformação plástica
%alongamento=
(lf-lo/lo)x100
onde lo e lf correspondem
ao comprimento inicial e
final (após a ruptura),
respectivamente
Ductilidade em termos de alongamentoDuctilidade em termos de alongamento
ductilidade
Outras informações que podem ser obtidas das
curvas tensãoxdeformação

28
Ductilidade expressa como
alongamento
 Como a
deformação final é
localizada, o valor
da elongação só
tem significado se
indicado o
comprimento de
medida
 Ex: Alongamento:
30% em 50mm

29
Ductilidade expressa como
estricção
 Corresponde à redução na área da seção
reta do corpo, imediatamente antes da
ruptura
 Os materiais dúcteis sofrem grande
redução na área da seção reta antes da
ruptura
Estricção= área inicial-área final
área inicial

30
ResiliênciaResiliência
 Corresponde à capacidade do
material de absorver energia
quando este é deformado
elasticamente
 A propriedade associada é
dada pelo módulo de resiliência
(Ur)
Ur= σesc
2
/2E
 Materiais resilientes são
aqueles que têm alto limite de
elasticidade e baixo módulo de
elasticidade (como os materiais
utilizados para molas)
σesc

31
TenacidadeTenacidade
 Corresponde à capacidade
do material de absorver
energia até sua ruptura
tenacidade

32
Algumas propriedades
mecânicas para alguns metais

33
VARIAÇÃO DA PROPRIEDADES
MECÂNICAS COM A TEMPERATURA

34
TENSÃO E DEFORMAÇÃO
REAIS OU VERDADEIRAS
• A curva de tensão x
deformação convencional,
estudada anteriormente,
não apresenta uma
informação real das
características tensão e
deformação porque se
baseia somente nas
características
dimensionais originais do
corpo de prova ou amostra
e que na verdade são
continuamente alteradas
durante o ensaio.

35
TENSÃO E DEFORMAÇÃO
VERDADEIRAS
TENSÃO REAL (σr)
 σr = F/Ai
onde Ai é a área da
seção transversal
instantânea (m2
)
DEFORMAÇÃO REAL (εr)
 d ε r = dl/l
 ε r = ln li/lo
Se não há variação de
volume
Ai.li = Ao.lo
 ε r = ln Ai/Ao

36
RELAÇÕES ENTRE TENSÕES E
DEFORMAÇÕES VERDADEIRAS E
CONVENCIONAIS
RELAÇÃO ENTRE
TENSÃO REAL E
CONVENCIONAL
σr = σ (1+ ε)
RELAÇÃO ENTRE
DEFORMAÇÃO REAL E
CONVENCIONAL
ε r = ln (1+ ε)
Estas equações são válidas para situações até
a formação do pescoço

37
TENSÃO CORRETA PARA A REGIÃO
ONDE INICIA-SE A FORMAÇÃO DO
PESCOÇO
σr = kεn
K e n são constantes
que dependem do
material e dependem
do tratamento dado
ao material, ou seja,
se foram tratados
termicamente ou
encruados
correta
A tensão correta de ruptura é
devido a outros componentes
de tensões presentes, além da
tensão axial

38
Outras propriedades
mecânicas importantes
 Resistência ao impacto
 Dureza
 Fluência
 Fratura Serão vistos posterirormente
 Fadiga

39
K e n
 K= coeficiente de resistência
(quantifica o nível de resistência que
o material pode suportar)
 n= coeficiente de encruamento
(representa a capacidade com que o
material distribui a deformação)

40
Determinação de K e n
Log σr =log k+ n log εr
Para εr= 1 σr =k
1
K
Inclinação= n
σr
εr
extrapolando

41

6 propriedades mecanicas (1)

Mais conteúdo relacionado

Mais procurados

Semelhante a 6 propriedades mecanicas (1)

Último

6 propriedades mecanicas (1)