Baixar para ler offline
Carregado porJoao Rosa
Aula 33 a 35
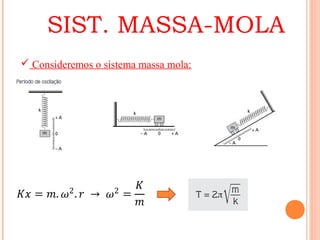
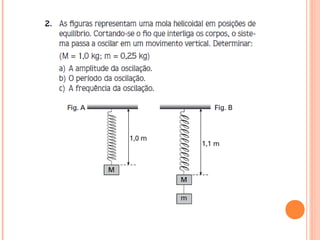
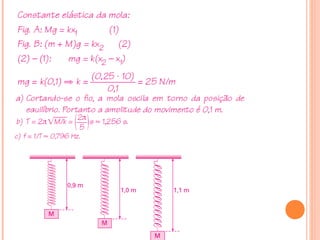
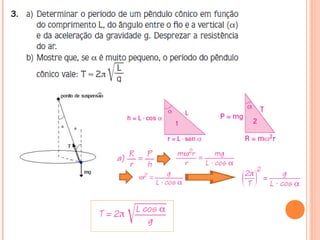
O documento discute dois sistemas mecânicos: (1) um sistema massa-mola, onde a força restauradora é proporcional ao deslocamento da massa; (2) um pêndulo simples, onde a força restauradora é tangencial à coordenada angular e proporcional a esta para pequenos deslocamentos, e cuja frequência angular é inversamente proporcional à raiz quadrada do comprimento do pêndulo.
Aula 33 a 35
- 1. AULA 33 A35 – PÁG: 39/ AP. 04 PROF. JOÃO ROSA. MECÂNICA
- 2. Consideremos osistema massa mola: SIST. MASSA-MOLA 𝐾� = �. �2 . � → �2 = 𝐾 �
- 3.
- 4.
- 7. Consideremos umpêndulo simples, como sendo um corpo de massa m suspensa por um fio ou haste de comprimento l e massa desprezível. A força restauradora é a componente tangencial da força resultante: para pequenos deslocamentos logo PÊNDULO SIMPLES θθ mgsenF −= θθ =sen x L mg mgF −=−= θθ A força restauradora é proporcional a coordenada para pequenos deslocamentos e k = mg/L.
- 8. A freqüênciaangular (ω) de um pêndulo simples com amplitude pequena será L g m Lmg m k === / ω A freqüência (f) e o período (T) correspondente são: g L f T L g f π ω π ππ ω 2 12 2 1 2 === == PÊNDULO SIMPLES