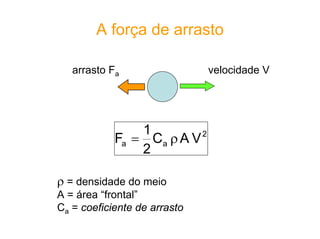
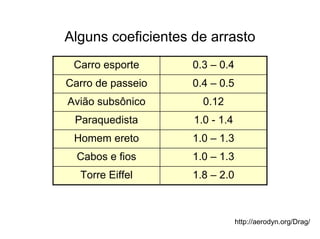
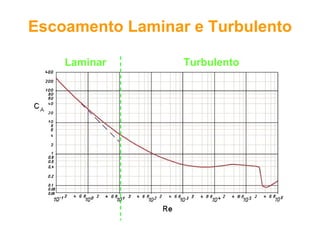
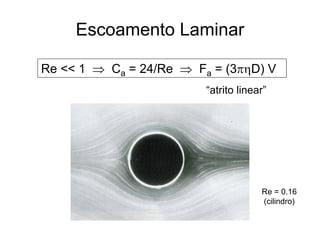
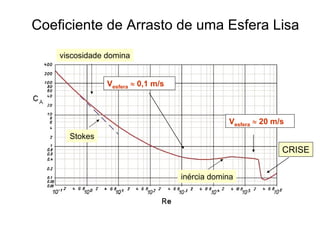
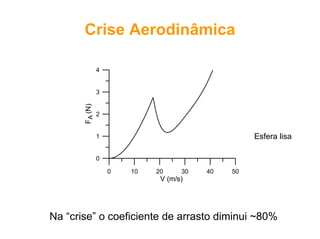
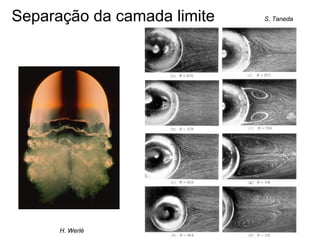
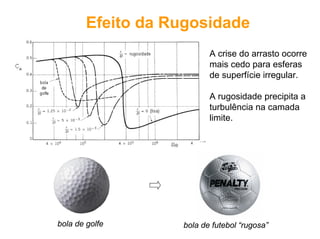
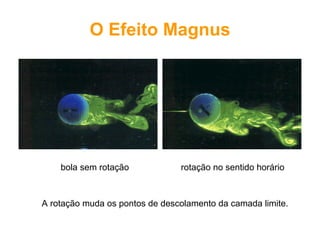
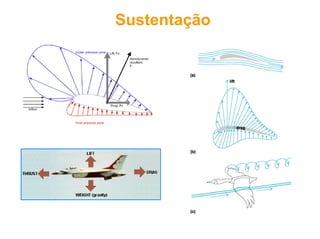
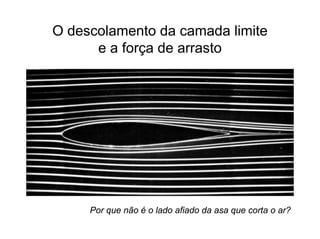
O documento discute conceitos fundamentais de dinâmica de fluidos como escoamento laminar e turbulento, número de Reynolds, coeficiente de arrasto e força de Magnus. Trata da influência da camada limite, rugosidade e rotação no arrasto de corpos em escoamento.