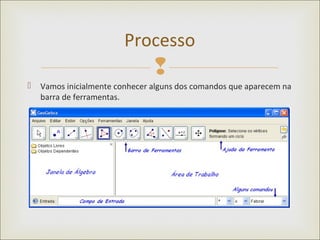
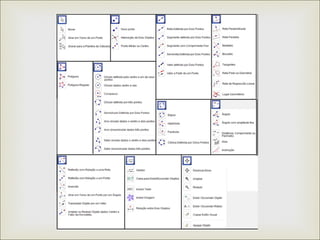
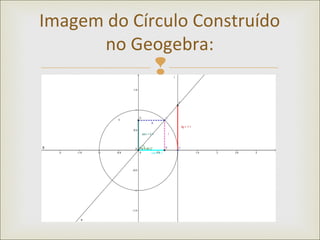
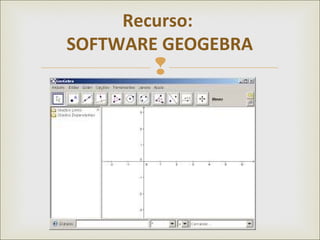
Este documento apresenta uma webquest sobre trigonometria utilizando o software Geogebra. Ele tem como objetivos desenvolver conceitos trigonométricos através da construção do círculo trigonométrico no Geogebra e aplicar estas noções na resolução de problemas. A atividade guiará os alunos passo a passo na construção do círculo e na exploração de suas funções para preencher tabelas e responder perguntas.

1. André Luis BrazAndré Luis Braz
Catia Aparecida PtucienikCatia Aparecida Ptucienik
Geisi De Oliveira PominaGeisi De Oliveira Pomina
Geisi O. PominaGeisi O. Pomina
Percia SchultzPercia Schultz
Rosangela de Freitas dos SantosRosangela de Freitas dos Santos

2. 
Esta Webquest tem por objetivo:
•Elaborar ideias acerca das atividades propostas com a construção do circulo
trigonométrico.
•Identificar os valores de seno e cosseno em diferentes ângulos.
•Identificar a medida de ângulos a partir da indicação de diferentes valores de
sen e cos.
•Identificar a relação entre as medidas dos lados e dos ângulos de um triângulo
retângulo.
•Desenvolver o conceito de razões trigonométricas.
•Aplicar as razões trigonométricas na resolução de situações-problema.
•Compreender que as razões trigonométricas podem ser trabalhadas como
funções trigonométricas a partir do círculo trigonométrico.
Introdução

3. 
 Para desenvolver esta atividade utilizaremos o recurso tecnológico-
software Geogebra, para realizar a construção do circulo
trigonométrico e explorar as funções trigonométricas seno e
cosseno. Trata-se de uma atividade de cunho investigativo capaz de
promover o aprendizado, formalização de conceitos e elaboração de
significados por parte do aluno.
 O GeoGebra é um software de Geometria Dinâmica desenvolvido
por MarkusHohenwarter da Universidade de Salzburg para utilização
nas escolas. O mesmo pode ser também utilizado na Geometria
Analítica, no estudo de propriedades de retas, parábolas, vetores,
cônicas, etc.
Tarefa

4. 
 Vamos inicialmente conhecer alguns dos comandos que aparecem na
barra de ferramentas.
Processo

6. 
Em seguida deverá ser entregue para os alunos uma folha com os passos que
deverão ser seguidos para realizar a construção do circulo trigonométrico no
Geogebra:
Construção do Circulo Trigonométrico no software Geogebra.
a) Exibir eixo
b) Ampliar
c) Deslocar eixos .
d) Clicar no ícone e sobre o ponto de intersecção entre os eixos (0,0).
e) Selecione a opção “Círculo dados centro e raio”, clique no ponto A e digite,
na janela que se abrirá, o valor 1. Clique em OK.
f) Clicar no ícone e sobre o ponto de intersecção entre os eixos (0,1). Criou o
Ponto B. O que representa o segmento ?
- Questionar aos alunos sobre o valor do raio da circunferência, levando-os a
perceber o porquê de ser 1 unidade.
Processo

7. g) Clicar no ícone “Reta definida por dois pontos”, em seguida no pontoA
(0,0) e em um ponto da circunferência. O Ponto de intersecção da reta com a
Circunferência foi chamado de Ponto C.
h) Clicar no ícone , em seguida no ponto B, no ponto A e no ponto C,
indicando assim a medida do ângulo formado pelos segmentos.
i) Clicar em Opções, arredondamento, 1 casa decimal.
j) Clicar no ícone “Reta paralela” e em seguida em um ponto do Eixo da
Ordenada e no Ponto C. Clicar no ícone “segmento definido por dois pontos”,
em seguida clicar no ponto de intersecção da reta construída com o Eixo da
Abscissa e no ponto C, formando o segmento . Clicar com o botão direito
sobre o segmento, Propriedades, Cor e Estilo (Pontilhado). Clicar sobre esta
reta (fora da circunferência) com o botão direito e Exibir objeto (Vai esconder a
reta, ficando apenas o segmento .
k) Clicar no ícone “Reta paralela” e em seguida em um ponto do Eixo da
Abscissa e no Ponto C. Clicar no ícone “segmento definido por dois
pontos”, em seguida clicar no ponto de intersecção da reta construída com o
Eixo da Ordenada e no ponto C, formando o segmento . Clicar com o botão
direito sobre o segmento, Propriedades, Cor e Estilo (Pontilhado). Clicar sobre
esta reta (fora da circunferência) com o botão direito e Exibir objeto (Vai
esconder a reta, ficando apenas o segmento .

8. l) Clicar no ícone “segmento definido por dois pontos”, em seguida clicar no
ponto A e no ponto E, formando o segmento .
m) Clicar com o botão esquerdo do mouse sobre o segmento , em seguida
em propriedades, básico, exibir rotulo, valor, alterar a cor e estilo, então fechar.
Aparecerá um valor, o que representa?
n) Clicar com o botão direito sobre o segmento , Renomear Sen. Em
Propriedade, Exibir Rótulo, Nome & Valor.
o) Clicar no ícone “segmento definido por dois pontos”, em seguida clicar no
ponto A e no ponto D, formando segmento .
p) Clicar com o botão esquerdo do mouse sobre o segmento , em seguida em
propriedades, básico, exibir rotulo, valor, alterar a cor e estilo, então fechar.
Aparecerá um valor, o que representa?
q) Clicar com o botão direito sobre o segmento , Renomear Cosen. Em
Propriedade, Exibir Rótulo, Nome & Valor.
r) Clicar no ícone “Reta paralela” e em seguida em um ponto do Eixo da
Ordenada e no Ponto B (1,0). Vai traçar uma reta paralela ao Eixo y, adjacente a
circunferência.

9. t) Clicar no ícone “Segmento definido por Dois Pontos” , no Ponto B e no
Ponto F.
u) Clicar com o botão direito sobre o Segmento , clicar em Propriedades,
Básico, Exibir Rótulo, Valor. Ainda nesta janela clicar em Cor e determinar
uma outra cor para este segmento. Aparecerá um valor, o que representa?
v) Clicar com o botão direito sobre o segmento , Renomear Tg. Em
Propriedade, Exibir Rótulo, Nome & Valor.
w) Clicar no ícone “Mover” e em seguida mover o ponto B. Observar o que
acontece.
Após a construção do círculo trigonométrico no Geogebra, deverá ser
entregue aos alunos uma folha com algumas instruções que deverão ser
exploradas no Geogebra e a partir disto os mesmos deverão preencher uma
tabela.

10. 
Imagem do Círculo Construído
no Geogebra:

11. 1) Com o auxilio do software Geogebra, complete a tabela abaixo com
valores aproximados. Para isso, clique no ícone mover, em seguida
no ponto D e arraste o ponto com o mouse pela circunferência até
chegar aos ângulos indicados na tabela:
Atividades que serão desenvolvidas a partir
da exploração do círculo no Geogebra:
Ângulo (α) Sen(α) Cos(α)
0º
30º
45º
90º
120º
180º
210º
270º
300º
330º
360º

12. 2) Responda:
a) Ao clicar no ícone “Mover”, no ponto D e arrastando o ponto com o mouse
pela circunferência, o que você observou?
b) Quando o valor do seno for 0,91, qual será o ângulo?
c) Quando o valor do cosseno for 0,85, qual será o ângulo?
d) Quando o valor do seno for 0, qual será o ângulo?
e) Quando o valor do cosseno for 0, qual será o ângulo?
f) Quando aumentamos o valor do ângulo, o que acontece com o valor do sen! E
do cos!
3) Considerando os eixos que dividem os quadrantes, complete a tabela abaixo
com o sinal negativo ou positivo:
Quadrante sen(±) cos(±)
1º
2º
3º
4º

13. 4) Responda:
a) O ângulo de 150º está em qual quadrante? Neste ângulo, quais são os
valores de seno e cosseno? São positivos ou negativos?
b) O ângulo de 60º está em qual quadrante? Neste ângulo, quais são os
valores de seno e cosseno? São positivos ou negativos?
c) O ângulo de 215º está em qual quadrante? Neste ângulo, quais são os
valores de seno e cosseno? São positivos ou negativos?
d) O ângulo de 315º está em qual quadrante? Neste ângulo, quais são os
valores de seno e cosseno? São positivos ou negativos?
e) O ângulo de 90º está em qual quadrante?
f) Para que valores de ângulos, o sen vale 1? E o cos?

14. 
Recurso:
SOFTWARE GEOGEBRA

15. 
 Avaliar a participação e o desenvolvimento dos alunos no
decorrer das atividades propostas, pedir aos alunos que
façam uma analise sobre as atividades realizadas no
Software Geogebra, apontando os benefícios que essa
atividade trouxe no processo de aprendizagem a qual
devera entregue.
Avaliação

16. 
 Existem inúmeras metodologias para se trabalhar com o ensino e
aprendizagem de matemática, metodologias que possibilitam aulas
mais dinâmicas, envolventes, desafiadoras. As Atividades
Investigativas são uma dessas metodologias, que transformam as
aulas, mais especificamente os conteúdos de matemática muito mais
interessantes, pois desafia o aluno a buscar respostas para os
problemas apresentados, instiga-os a querer sempre mais.
 É nesta perspectiva que propomos a utilização do Software Geogebra
como ferramenta em uma atividade investigativa, e acreditamos que
é possível promover uma aprendizagem valiosa, cheia de significados
e apropiação.
Conclusão