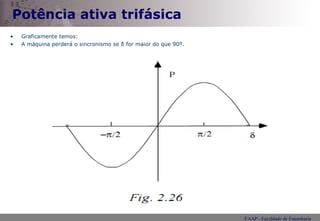
O documento apresenta os principais conceitos sobre máquinas síncronas, incluindo: 1) curva de magnetização e efeito da histerese; 2) modelo matemático com circuito equivalente; 3) diagramas fasoriais para gerador e motor síncrono; 4) conceito de ângulo de potência e quadrantes de potência.

1. Máquina síncrona – Segunda parte Professor Jim Naturesa

2. Introdução Curva de magnetização da máquina síncrona. A variação de Ef por If é mostrada na figura abaixo.

3. Introdução Curva de magnetização da máquina síncrona – efeito da histerese e saturação.

4. Introdução Se os terminais do estator forem conectados a uma carga trifásica, uma corrente Ia aparecerá. As correntes de estator estabelecem um campo no entreferro – chamado reação da armadura. O fluxo no entreferro é resultado dos fluxos produzidos pela corrente de campo If e pela corrente de armadura Ia.

5. Introdução O fluxo resultante Φ r assumindo a não saturação vale: Φ r = Φ f + Φ a Onde Φ f é o fluxo devido ao campo (If), Φ a é o fluxo devido a armadura (Ia). Observação: a freqüência da corrente de armadura (Ia) é a mesma da tensão de excitação (Ef).

6. Modelo matemático da máquina síncrona Modelo da máquina síncrona – circuito equivalente. O modelo da máquina síncrona é apresentado abaixo. Onde: Xs é a reatância síncrona (Ohms), Ra é a resistência de armadura (Ohms).

7. Modelo - Gerador Gerador síncrono. Vt é a tensão terminal - referência. A corrente de armadura (Ia) e o seu respectivo ângulo ( Φ ) são conhecidos. Temos: Ef = Vt + Ia (Ra + j Xs) = l Ef l L δ

8. Modelo – Gerador Abaixo o diagrama fasorial do gerador síncrono. Foi desconsiderado a resistência de armadura (Ra).

9. Modelo - Motor Motor síncrono. Vt é a tensão terminal - referência. A corrente de armadura (Ia) e o seu respectivo ângulo ( Φ ) são conhecidos. Temos: Vt = Ef + Ia (Ra + j Xs) Ef = Vt – Ia (Ra + j Xs) = l Ef l L- δ

10. Modelo - Motor Abaixo o diagrama fasorial do motor síncrono. Foi desconsiderado a resistência de armadura (Ra).

11. Modelo – ângulo de potência O ângulo δ é conhecido como o ângulo de potência . Se δ for maior do que zero, temos a ação geradora. Se δ for menor do que zero, temos a ação motora. O ângulo δ é importante para a transferência de potência e para a estabilidade da máquina síncrona.

12. Quadrante de potência

13. Potência complexa Conceito de potência complexa. Considere o circuito abaixo.

14. Potência Temos os fasores: A corrente conjugada vale:

15. Potência A impedância vale: Z = a+jb e o seu conjugado vale Z * = a-jb A potência complexa vale: S = V I * , que possui uma propriedade muito útil, o que pode ser confirmado pela substituição de I*.

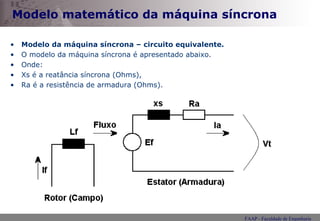
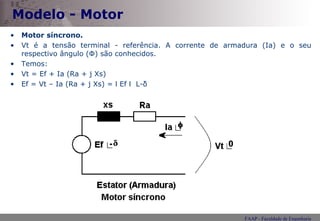
16. Potência O ângulo de fase (V-I) é o ângulo Φ , logo: Logo S = P + j Q onde: P = S cos( Φ ) [W] e Q = S sen( Φ ) [Var]

17. Potência Normalmente a máquina síncrona é conectada a um barramento com uma tensão e rotação (velocidade) constante. Existe um limite para a potência injetada (caso do gerador) e para o torque aplicado (motor) sem a perda de sincronismo.

18. Potência Temos:

19. Potência A potência aparente do circuito anterior é dada por: Onde:

20. Potência Podemos escrever:

21. Potência Da equação de potência: Logo as potências ativa e reativas podem ser escritas como:

22. Potências ativa e reativa

23. Potência trifásica ativa Se Ra for desconsiderado temos Zs = Xs e θ s = 90 º. Para um sistema trifásico temos:

24. Potência ativa trifásica Graficamente temos: A máquina perderá o sincronismo se δ for maior do que 90 º.

25. Potência reativa trifásica e torque de saída A potência reativa trifásica é dada por: O torque desenvolvido na máquina vale:

26. Torque

27. Curvas características As curvas características da máquina síncrona são apresentadas abaixo:

28. Referências Carvalho, G. Máquinas Elétricas – Teoria e Ensaios . Editora Érica. Flarys, F. Eletrotécnica Geral – Teoria e Exercícios Resolvidos. Editora Manole. Kirtley Jr., J. Introduction to Power System . Synchronous Machine and Winding Models . Massachusetts Institute of Technology. http://ocw.mit.edu/index.html Kuznetsov, M. Fundamentals of Electrical Engineering . Peace Publishers - Moscow. Marques, G. Máquinas Elétricas . Capítulo 2 – Máquinas Síncronas. http://paginas.terra.com.br/educacao/profarana/apoio/apoio.htm Sen, P. Principles of Electric Machines and Power Electronics. John Wiley and Sons. Yamayee, Z. & Bala Jr, J. Electromechanical Energy Devices and Power Systems . John Wiley and Sons.