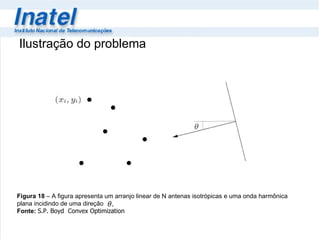
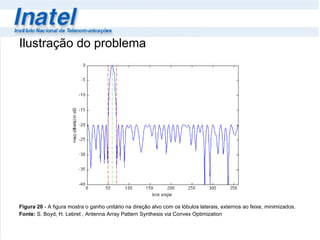
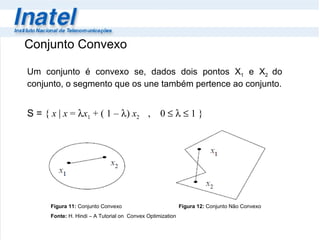
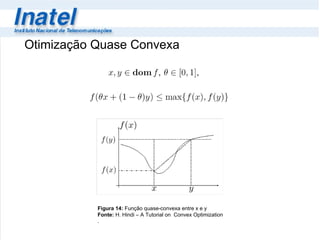
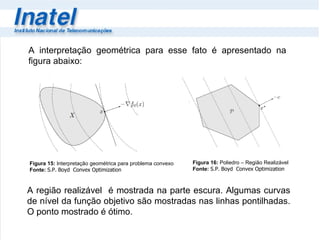
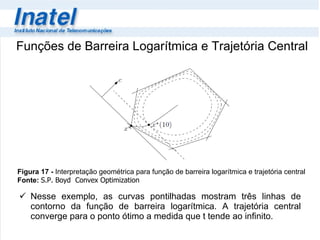
O documento discute a otimização convexa, resumindo: 1) A otimização convexa busca encontrar soluções ótimas globais, ao contrário da quase convexa que pode ter soluções locais não ótimas. 2) O método de pontos interiores é eficiente para problemas convexa, minimizando funções através de pontos dentro da região viável. 3) Funções de barreira logarítmica reformulam restrições para aplicar o método de Newton e encontrar a trajetória central do problema original.

1. Seminário Introdução à Otimização Convexa Resolução de problemas utilizando CVX Guilherme Varela Barbosa Rodrigo Carneiro Brandão Rodrigo de Oliveira Matos

2. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

3. Breve Histórico de Otimização 1939-1945: A otimização teve início durante a 2 a Guerra Mundial. 1947: Início do interesse das indústrias na utilização das técnicas desenvolvidas na área militar, para auxiliar no planejamento e controle da produção. 1949: George B. Dantzig apresenta o Método Simplex para resolver problemas de otimização linear (equações e (ou) inequações lineares).

4. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

5. Otimização Harrel et al. (2000) define otimização como o processo de tentar diferentes combinações de valores para variáveis que podem ser controladas (variáveis independentes), buscando a combinação de valores que leva à saída mais desejada. De acordo com Torga (2007), a procura pela solução ótima pode ser conduzida manualmente ou automatizada com algoritmos especialmente designados para procurar a solução ótima sem executar a avaliação de todas as soluções possíveis.

6. Alguns métodos de otimização: Programação Linear Programação Não-Linear

7. Programação Linear Distribuição eficiente de recursos limitados para atender um determinado objetivo. Função linear: suas variáveis possuem relações proporcionais entre si.

8. Programação Linear 20 15 10 5 5 10 x y Figura 1: Gráfico da função y = 2x Exemplo: Função y = 2x , y = f(x) , x = Valores de 0 a 10 2 * X = Y 2 * 0 = 0 2 * 1 = 2 2 * 2 = 4 2 * 3 = 6 2 * 4 = 8 2 * 5 = 10 2 * 6 = 12 2 * 7 = 14 2 * 8 = 16 2 * 9 = 18 2 * 10 = 20

9. Programação Não-Linear Finalidade: resolver problemas que envolvem funções constituídas de variáveis que compartilham relações desproporcionais entre si (não-linearidade). Uma função é considerada não linear quando uma ou mais de suas variáveis possuem relações desproporcionais entre si.

10. Programação Não-Linear Figura 2: Gráfico da função y = X 2 Exemplo: Função y = x 2 , y = f(x) , x = Valores de 0 a 10 X 2 = Y 0 2 = 0 1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100

11. De acordo com Winston (2001), para determinar se o problema de PNL possui solução ótima ou não, é necessário definir a função de concavidade e convexidade . Programação Não-Linear

12. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

13. Funções Função Convexa Inclinação na região é sempre crescente; A linha que conecta dois pontos na função nunca se estende abaixo dela. Figura 3: Função estritamente convexa Figura 4: Função convexa Fonte: H. Hindi – A Tutorial on Convex Optimization

14. São exemplos de funções convexas: Figura 5: Função convexa Figura 6: Função convexa

15. Função Côncava Inclinação na região é sempre decrescente; A linha que conecta dois pontos na função nunca se estende acima dela. Funções Figura 7: Função estritamente côncava Figura 8: Função côncava Fonte: H. Hindi – A Tutorial on Convex Optimization

16. São exemplos de funções côncavas: Figura 9: Função côncava Figura 10: Função côncava

17. Funções Análise matemática de Função Convexa e Côncava Função Convexa F( λ(x 1 )+(1- λ)x 2 ) ≤ λ F (x 1 )+(1- λ) F(x 2 ) Função Côncava F( λ(x 1 )+(1- λ)x 2 ) ≥ λ F (x 1 )+(1- λ) F(x 2 )

18. Conjunto Convexo Um conjunto é convexo se, dados dois pontos X 1 e X 2 do conjunto, o segmento que os une também pertence ao conjunto. S = { x | x =  x 1 + ( 1 –  ) x 2 , 0  1 } Figura 11: Conjunto Convexo Figura 12: Conjunto Não Convexo Fonte: H. Hindi – A Tutorial on Convex Optimization

19. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

20. Otimização Convexa - Formulação geral

21. Otimização convexa Parâmetros para um problema ser considerado convexo: Função Objetivo ( funções convexas); Inequações de Restrições ( funções convexas); Equações de Restrições ( funções afins). E deve-se minimizar uma função objetivo convexa sobre um conjunto convexo.

22. Problemas: Muitos pontos locais “ótimos”; Difícil encontrar um ponto ótimo (X*) que satisfaça todas as restrições; Critérios de parada, muitas vezes aleatórias; Algoritmos de baixa taxa de convergência; Problemas numéricos faziam com que os algoritmos de minimização parassem em vários pontos ou ficassem flutuando. Otimização Convexa Evolução nas técnicas de Otimização Convexa visando obter os parâmetros para a formulação adequada:

23. Segundo D.P. Bertrekas (1999) Se : Sujeito a fi (x) (convexas) hi (x) (afins) Os três primeiros problemas são eliminados Mesmo assim : A baixa taxa de convergência permanece como problema.

24. De acordo com A. Nemirovskii (1994) , até o final dos anos 80 e 90, foi descoberto na antiga União Soviética e Estados Unidos que: Se: fi (x) (além de convexas) fosse baseada no método de pontos interiores , o problema de baixa taxa de convergência seria evitado .

25. Otimização convexa Base matemática:

26. Otimização Quase Convexa

27. Otimização Quase Convexa Figura 13: Função quase convexa Fonte: H. Hindi – A Tutorial on Convex Optimization

28. Figura 14: Função quase-convexa entre x e y Fonte: H. Hindi – A Tutorial on Convex Optimization . Otimização Quase Convexa

29. Quase Convexa - Diferen ç a Importante Um problema de otimização quase convexa pode ter soluções ótimas locais que não são (globalmente) ótimas. O que não ocorre na otimização convexa, uma vez que, uma solução ótima local é também uma solução ótima global.

30. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

31. Problemas de Otimização Convexa (Forma Padrão) O problema encontra-se na forma padrão A inequação de restrição não é convexa Não. A equação de restrição não é afim

32. Problemas de Otimização Convexa (Forma Padrão)

33. A interpretação geométrica para esse fato é apresentado na figura abaixo: Figura 15: Interpretação geométrica para problema convexo Fonte: S.P. Boyd Convex Optimization A região realizável é mostrada na parte escura. Algumas curvas de nível da função objetivo são mostradas nas linhas pontilhadas. O ponto mostrado é ótimo. Figura 16: Poliedro – Região Realizável Fonte: S.P. Boyd Convex Optimization

34. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

35. Algoritmos de resolução geral A idéia de que os problemas de otimização convexa eram factíveis e que, a teoria da otimização convexa é mais simples e mais completa do que a teoria geral da otimização não-linear não é recente. Diversos métodos como, por exemplo, método do sub-gradiente, método de planos cortados e método do elipsóide foram desenvolvidos na União Soviética entre 1960 e 1970. Apesar desses métodos serem algoritmos de resoluções universais para otimização convexa, funcionando até mesmo para funções não diferenciável, eles não são eficientes.

36. Método de Pontos interiores Útil para problemas de: Programação linear Programação geométrica Programação quadrática Além de lidar com problemas de forma cônica. Método mais eficiente de resolução de problemas - Quase independente do tipo e do tamanho do problema. Cada iteração envolve a resolução de um conjunto de equações lineares (problemas de mínimos quadrados) com o mesmo tamanho e estrutura do problema.

37. Método de Pontos interiores Busca chegar a uma solução ótima caminhando através de pontos interiores da região realizável. Baseado no método de Newton e na Função Logarítmica de Barreira – Aplica funções que atuam como barreiras armazenando as variáveis em pontos interiores a região realizável. Técnica para resolver um problema cuja restrição é uma equação linear, e a função objetivo é duas vezes diferenciável. O usuário deve fornecer uma tolerância desejável para o vetor de decisão.

38. Método de Newton para Problemas de Minimização com Restrições de Igualdade.

39. Funções de Barreira Logarítmica e Trajetória Central O objetivo é reformular as inequações de restrição do problema, de tal forma que seja possível aplicar o método de Newton. Torne as restrições de inequação implícitas na função objetivo. Para isso, uma função de barreira é adicionada na função objetivo, tal como a função de barreira logarítmica : O problema fica da seguinte forma:

40. Funções de Barreira Logarítmica e Trajetória Central A medida que o parâmetro t é incrementado, mais o problema reformulado se aproxima do problema original. Por outro lado, quanto maior o valor de t, mais difícil se torna minimizar a função pelo método de Newton, uma vez que, o Hessiano varia mais rapidamente próximo da fronteira da região realizável. O gradiente e o hessiano da função de barreira logarítmica é dado, respectivamente por:

41. Funções de Barreira Logarítmica e Trajetória Central Agora, multiplicando-se a função objetivo por t, teremos o seguinte problema equivalente: Minimizar: Sujeito a: De modo que o novo problema possa ser resolvido pelo método de Newton e que possua apenas uma única solução para cada . A trajetória central, associada com o problema original, é definida como o conjunto de pontos que garantem as condições necessárias e suficientes exigidas nas restrições do problema original. Assuma que

42. Funções de Barreira Logarítmica e Trajetória Central Nesse exemplo, as curvas pontilhadas mostram três linhas de contorno da função de barreira logarítmica. A trajetória central converge para o ponto ótimo a medida que t tende ao infinito. Figura 17 - Interpretação geométrica para função de barreira logarítmica e trajetória central Fonte: S.P. Boyd Convex Optimization

43. Método da barreira

44. Funções auto-concordantes Importante pois: Incluem a função de barreira logarítmica que apresenta grande importância no Método de Pontos Interiores. A analise do Método de Newton para funções auto-concordantes não depende de constantes desconhecidas. Se realizarmos uma transformação linear de variável em uma função auto-concordante, teremos uma função auto-concordante. Uma função convexa é auto-concordante se

45. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

46. O que é o CVX? CVX fornece métodos para simplificar a construção de problemas e obedece um conjunto de regras denominada DCP. Modos de construção de problema SDP – Programação Semidefinida Positiva Utiliza uma matriz de inequações lineares (LMIs) GP – Programação Geométrica Aceita todas as funções e regras da programação convexa . Plataforma - MatLab

47. O que o CVX não é? O CVX não é uma ferramenta para: Verificar se determinado problema é convexo ou não. Resolução de problemas de larga escala.

48. Programação Convexa Disciplinada A programação convexa disciplinada é uma metodologia destinada a construção de problemas de otimização convexa proposta por Michael Grant, Stephen Boyd e Yinyu Ye. Problemas que aderem a esse conjunto de regras DCP podem ser resolvidos rapidamente. Porém, os problemas que violam essas regras são rejeitados, mesmos que esses problemas sejam convexos.

49. Inicialização As especificações do CVX no prompt de comando do MatLab são precedidas por cvx_begin e finalizadas por cvx_end. As variáveis de otimização não possuem valor numérico. Elas são caracterizadas como objetos. Caso alguma regra seja violada, uma mensagem de erro é gerada. Caso contrário, as especificações são convertidas para a forma canônica e solucionadas.

50. Panorama do conjunto de regras DCP Como vimos anteriormente o conjunto de regras DCP retorna uma mensagem de erro quando uma de suas regras é violada. Esse conjunto de regras é suficiente, porém incompleto, para garantir que determinada função seja convexa, ou seja, é possível elaborar expressões que violem essas regras e que sejam de fato convexas.

51. Conjunto de Regras DCP Regras de alto nível O CVX suporta dois diferentes tipos de programação convexa disciplinada. Problemas de minimização É necessário que a função objetivo seja convexa e nenhuma ou mais restrições. Problemas de maximização É necessário que a função objetivo seja côncava e nenhuma ou mais restrições.

52. Restrições Três tipos de restrições podem ser especificadas no DCP: Restrição de igualdade == Ambos os lados são afim (um ou ambos os lados podem ser complexos). Restrição de desigualdade menor que <= O lado esquerdo é convexo e o lado direito é côncavo (ambos os lados deve ser real) . Restrição de desigualdade maior que >= O lado esquerdo é côncavo e o lado direito é convexo (ambos os lados deve ser real).

53. Funções As funções são caracterizadas por dois atributos. Curvatura Pode ser constante, afim, convexa ou côncava. Determina as condições pela qual as expressões entram em concordância com as regras de expressões. Monotonicidade Pode ser não-crescente, não-decrescente ou não-monótona. Determina como as expressões podem ser usadas para a criação de funções.

54. Compondo Funções Regras de composição para funções convexas: Se a função possui argumento não-decrescente, este argumento deve ser convexo. Se a função possui argumento não-crescente, esse argumento deve ser côncavo. Regras de composição para funções côncavas: Se a função possui argumento não-decrescente, este argumento deve ser côncavo. Se a função possui argumento não-crescente, esse argumento deve ser convexo.

55. Dados de entrada m = 16; n = 8; A = randn(m,n); b = randn(m,1); Solução através do Matlab x_ls = A \ b; Solução através do cvx cvx_begin; variable x(n); minimize(norm(A*x-b) ); cvx_end; Mínimos-quadrados

56. Resultados: norm(A*x_ls-b): 2.0354 (Solução usando Mínimos Quadrados) norm(A*x-b): 2.0354 (Solução usando CVX) cvx_optval: 2.0354 cvx_status: Solved Verificando x_ls == x: x_ ls = [ -0.2628 0.8828 -0.0734 -1.0844 0.3249 -0.3330 0.0603 0.3802 ] x = [ -0.2628 0.8828 -0.0734 -1.0844 0.3249 -0.3330 0.0603 0.3802 ] Vetor resultado ( Utilizando CVX ): A*x-b = [ -0.3262 -0.0070 -0.9543 0.2447 -0.6418 -0.3426 -0.1870 0.2960 0.6024 -0.0440 0.6238 -0.7399 0.0849 0.9323 0.4799 -0.0762 ] Mínimos-quadrados

57. Dados de entrada bnds = randn(n,2); l = min( bnds, [ ] ,2 ); u = max( bnds, [ ], 2 ); Solução através do Quadprog x_qp = quadprog( 2*A'*A, -2*A'*b, [], [], [], [], l, u ); Solução através do CVX cvx_begin variable x(n); minimize( norm(A*x-b) ); subject to x >= l; x <= u; cvx_end Mínimos-quadrados com restrições

58. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

59. Arranjo de Antenas A título aplicação será demonstrado um problema de arranjos de antenas formulado por H. Lebret, S. Boynd e A. Mutapcic. Arranjos de antenas proporcionam um meio eficiente de detectar e processar sinais provenientes de diferentes direções. Comparando uma única antena, que é limitada em diretividade e largura de banda, um conjunto de sensores pode ter seu diagrama de irradiação modificado através de um distribuição de amplitude e fase denominada de pesos do arranjo. Após o processamento das saídas das antenas, os sinais são pesados e somados afim de fornecerem o diagrama de irradiação do arranjo. O problema em questão consiste em encontrar pesos que satisfaçam ao conjunto de especificações.

60. Arranjo de Antenas

61. Arranjo de Antenas

62. Ilustração do problema Figura 18 – A figura apresenta um arranjo linear de N antenas isotrópicas e uma onda harmônica plana incidindo de uma direção Fonte: S.P. Boyd Convex Optimization

63. Ilustração do problema Figura 19 – A figura A apresenta o diagrama de irradiação para um arranjo de antenas cuja diretividade não é particularizada. Fonte: S. Boyd, H. Lebret , Antenna Array Pattern Synthesis via Convex Optimization

64. Ilustração do problema Figura 20 - A figura mostra o ganho unitário na direção alvo com os lóbulos laterais, externos ao feixe, minimizados. Fonte: S. Boyd, H. Lebret , Antenna Array Pattern Synthesis via Convex Optimization

65. Ilustração do problema Figura 21: Diagrama de Irradiação para arranjo otimizado Fonte: S. Boyd, H. Lebret , Antenna Array Pattern Synthesis via Convex Optimization A figura 21 apresenta o diagrama de irradiação do arranjo após o processo de otimização e o vetor peso w.

66. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

67. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

68. Agradecimentos Agradecemos ao Prof. Dr. Dayan Adionel Guimarães (Inatel) pelo apoio e material disponibilizado; Ao Prof. Dr. Takaaki Ohishi (Unicamp) pela valiosa orientação e atenção; Ao Prof. Dr. Paulo Augusto Valente Ferreira (Unicamp) pela valiosa orientação e atenção.

69. Histórico Introdução Funções / Conjuntos Convexos Otimização Convexa Problemas de Otimização Métodos de Resolução CVX Aplicações Conclusão Agradecimentos Referências Bibliográficas

70. Referências Bibliográficas D.P. Bertrekas. Nolinear Programming . Athena Scientific,1999 HARREL, Charles R.; GHOSH, Biman K.; BOWDEN, Royce. Simulation Using ProModel . New York, McGraw-Hill, 2000. O.M Bucci, D. D’Elia, G. Mazzarella, and G. Panatiello, “Antenna pattern synthesis: A new approach,”Proc.IEEE, vol.82,pp.358-357, Mar. 1996. S.P. Boyd and L. Vandenberghe. Convex Optimization, Cambridge University Press, 2003. In press. Material avaible at www.stanford.edu/~boyd

71. TORGA, Bruno Lopes Mendes. Modelagem, Simulação e Otimização em Sistemas Puxados de Manufatura . Dissertação (Mestrado em Engenharia de Produção). UNIFEI. Itajubá-MG. 2007. WINSTON, Wayne; ALBRIGHT, S. Christian. Practical Management Science . 2nd, Duxbury Thomson Learning, 2001. Y. Nesterov and A. Nemirovskii. Interior-Point Polynomial Methods in Convex Programming . Society for Industrial and Applied Mathematics, 1994.