O documento discute a formulação de integrais de caminho em mecânica quântica, destacando sua importância para o estudo de sistemas quânticos e a evolução temporal. O método, desenvolvido por Richard Feynman, é útil na quantização e na resolução de expressões relacionadas a funções de Green. Exemplos práticos, como o oscilador harmônico, são apresentados para ilustrar a aplicação do propagador via integral de caminho.





































![Motivac¸ ˜ao
Formulac¸ ˜ao
Algumas referˆencias
Propagador via integral de caminho
Exemplo: Oscilador Harmˆonico
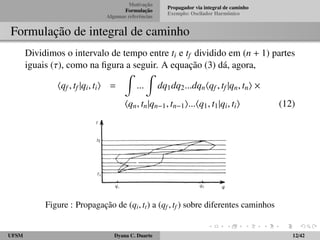
Formulac¸ ˜ao de integral de caminho
Escrevemos, de (13) (15) e (16):
hqj+1tj+1jqjtji =
1
h
Z
dpj exp
i
~
[pj(qj+1 qj) H(pj; ¯q)]
(17)
em que pj ´e o momento entre tj e tj+1 ou, de forma equivalente, qj e
qj+1. Essa equac¸ ˜ao nos d´a o propagador de um caminho poss´ıvel.
UFSM Dyana C. Duarte 16/42](https://image.slidesharecdn.com/seminariov2-141206111356-conversion-gate02/85/IntegracaoFuncional-40-320.jpg)
![Motivac¸ ˜ao
Formulac¸ ˜ao
Algumas referˆencias
Propagador via integral de caminho
Exemplo: Oscilador Harmˆonico
Formulac¸ ˜ao de integral de caminho
O propagador completo ´e dado substituindo em (12), no limite cont´ınuo
(em que pj ´e o momento ao longo do caminho entre qj e qj+1),
hqf tf jqitii = lim
n!1
Z Yn
j=1
dqj
Yn
j=0
dpj
h
exp
8:
i
~
Xn
j=0
[pj(qj+1 qj) H(pj; ¯qj)]
9=;
(18)
com q0 = qi, qn+1 = qf . De forma simb´olica:
hqf tf jqitii =
Z
DpDq
h
exp
i
~
Z tf
ti
dt[p˙q H(p; q)]
#
(19)
com q(ti) = qi; q(tf ) = qf .
UFSM Dyana C. Duarte 17/42](https://image.slidesharecdn.com/seminariov2-141206111356-conversion-gate02/85/IntegracaoFuncional-41-320.jpg)
