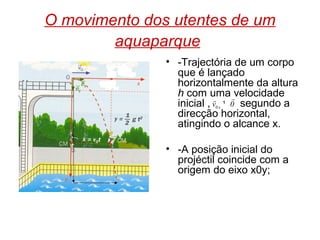
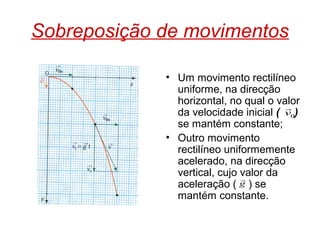
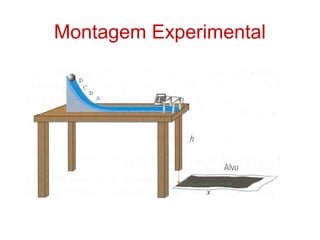
O documento discute como projetar um escorrega de aquaparque de modo que os usuários possam cair em segurança na água. Ele apresenta as equações de movimento para um corpo lançado horizontalmente com velocidade inicial a partir de uma altura, considerando movimento uniforme horizontal e aceleração vertical constante. Ele também discute experimentos para estudar a relação entre alcance e altura/velocidade inicial, usando sensores para medir o tempo de queda e calcular a velocidade.

2. Questão – Problema:
• Com o material indicado, tentar conceber
experiências que permitam projectar um
escorrega, para um aquapark, de modo
que os utentes possam cair em segurança
numa determinada zona da piscina. A
rampa termina num troço horizontal a uma
altura apreciável da superfície da água.

3. O movimento dos utentes de um
aquaparque
• -Trajectória de um corpo
que é lançado
horizontalmente da altura
h com uma velocidade
inicial , segundo a
direcção horizontal,
atingindo o alcance x.
• -A posição inicial do
projéctil coincide com a
origem do eixo x0y;
0xv 0¹
rr

4. Sobreposição de movimentos
• Um movimento rectilíneo
uniforme, na direcção
horizontal, no qual o valor
da velocidade inicial ( )
se mantém constante;
• Outro movimento
rectilíneo uniformemente
acelerado, na direcção
vertical, cujo valor da
aceleração ( ) se
mantém constante.
0v

g


5. Equações do movimento
• Equações do
movimento:
• Condições iniciais:
• eixo 0x:
• eixo 0y:
2
00
2
1
attvyy ++=
tvxx 00 +=
0x 0 m=
0y 0 ( m )=
0 yv 0 m / s=
hy =
00 vv x =

6. • As equações do
movimento são:
Onde
ga =
2
2
1
gth =
tvx 0=

7. Velocidade de lançamento/Alcance
horizontal
Substituindo na
equação:
⇔
21
h gt
2
= ⇔
tvx 0=
0v
x
t =
2
0
2
2
1
v
x
gh =

8. • Estudo da relação
entre o alcance e a
altura da queda de
uma esfera,
mantendo, para isso,
as mesmas
condições de
lançamento, e
fazendo variar a
altura da queda.
• Estudo da relação
entre o alcance e a
velocidade de
lançamento, fazendo,
para isso, variar as
condições de
lançamento e
mantendo a altura da
queda.
0
2
v
g
h
x =

9. Montagem Experimental
x

10. • Para saber o alcance, coloca-se sobre o chão
uma cartolina e um papel químico sobreposto
que assinalará essa posição. O alcance é a
medida entre a base da rampa e o ponto de
queda.
• A esfera vai demorar um certo intervalo de
tempo, , a percorrer a distância entre as
células fotoeléctricas colocadas uma na
extremidade da mesa e outra um pouco
distante, o qual é dado pelo Smart Timer.
• Pode-se, então, calcular da velocidade de saída
( ) do projéctil (esfera), através da expressão:0xv
r
t
x
v x
∆
∆
=0
t∆