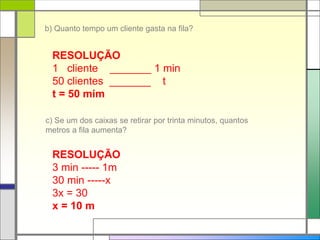
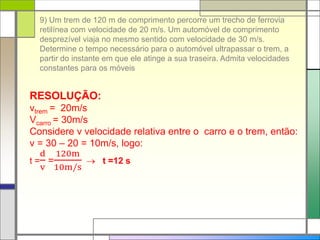
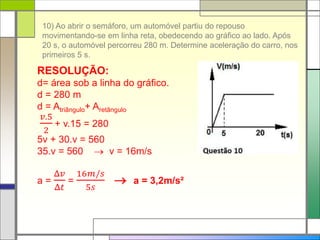
Este documento contém a resolução de 12 exercícios de física que envolvem cálculos de movimento com velocidade constante ou aceleração constante. Os exercícios cobrem tópicos como velocidade média, aceleração, tempo de encontro de objetos em movimento e distância percorrida.

1. MOVIMENTO
RESOLUÇÃO DA 1ª LISTA DE
EXERCÍCIOS COMPLEMENTARES

2. 1) Um rapaz dirige uma motocicleta a uma velocidade de 72 km/h,
quando aciona s freios e para em 1/12 min. Determine aceleração do
retardamento imprimida à motocicleta pelos freios.
RESOLUÇÃO:
v0= 72 km/h(expresse em m/s)
v0= 72:3,6 m/s = 20 m/s
v= 0 (parou)
t= 1/12 min( expresse em s)
t=
1
12
x 60 = 5 s
a =
∆𝑣
∆𝑠
=
0−20𝑚/𝑠
5𝑠
=
−20𝑚/𝑠
5𝑠
 a= – 4,0 m/s

3. RESOLUÇÃO:
São 03 caixas atendendo os clientes. Cada caixa
leva três minutos para atender a um cliente. Ao
passo que o primeiro caixa começa o
atendimento, os outros dois estarão atendendo a
dois clientes, cada um com um. Em três minutos
os três caixas atenderão a três pessoas. Cada
pessoa está distante 1metro uma da outra. Logo:
v =
∆𝑣
∆𝑡
=
3𝑚
3𝑚𝑖𝑚
 v= 1m/mim
2) Brasileiro sofre! Numa tarde de sexta-feira, a fila única de clientes de
um banco tem comprimento médio de 50m. Em média, a distância entre
as pessoas na fila é de 1,0m. Os clientes são atendidos por três caixas.
Cada caixa leva cerca de 3,0 min para atender um cliente. Pergunta-se:
a) Qual a velocidade (média) dos clientes ao longo da fila?

4. c) Se um dos caixas se retirar por trinta minutos, quantos
metros a fila aumenta?
b) Quanto tempo um cliente gasta na fila?
RESOLUÇÃO
1 cliente _______ 1 min
50 clientes _______ t
t = 50 mim
RESOLUÇÃO
3 min ----- 1m
30 min -----x
3x = 30
x = 10 m

5. 3) Determine o tempo necessário que um trem de 200m, a 72km/h passar
uma ponte de 50m de comprimento.
RESOLUÇÃO
v = 72 km/h  expresse em m/s
v = 72 : 3,6 = 20 m/s
d=200m + 50 m = 250 m
t =
𝐝
𝐯
=
𝟐𝟓𝟎𝐦
𝟐𝟎𝐦/𝐬
= 12,5 s

6. 4) Um automóvel passa por uma posição a 10 km de um ponto O,
afastando-se dele com velocidade constante de 84 km/h. Que
velocidade deve ter um motociclista que, neste instante, passa por O,
para alcançar o automóvel em 20 minutos?
RESOLUÇÃO
t = 20 mim =
1
3
h
d = v x t  d – 10km = 84km/h x
1
3
h
d = 28 km + 10 km = 38 km
Distância a ser percorrida pelo motociclista para alcançar
o carro.
v =
𝑑
𝑡
=
38 𝑘𝑚
1
3
ℎ
= 38 km x
3
1ℎ
 v = 114km/h

7. 5) A distância entre duas cidades, A e B, é de 200 km. De A, dirigindo-se
para B, parte um móvel, com velocidade constante de 40 km/h.
Simultaneamente, de B, dirigindo-se para A, parte outro móvel, com
velocidade também constante de 60 km/h. Determine o instante e a
posição do encontro.
RESOLUÇÃO
dA = vA.t  dA = 40.t
dB = 200 - vB.t  dB= 200 – 60.t
No encontro  dA = dB , para calcular o tempo de encontro.
40.t = 200 – 60.t  100t = 200
t = 200/100  t = 2,0 h
dA = 40.t dA = 40 km/h x 2,0 h
d = 80 km da cidade A

8. 6) Um barco parte de um porto A rumo a um porto B, viajando em linha
reta, com velocidade constante de 10 m/s. Simultaneamente outro barco
parte de B, rumo ao porto A, com velocidade de 5m/s. Sendo de 3600 m
a distância AB, em que instante e a que distância do porto A os barcos
vão se cruzar?
RESOLUÇÃO
dA = vA.t  dA = 10.t
dB = 3600 - vB.t  dB= 3600 – 5.t
No encontro  dA = dB , para calcular o tempo de encontro.
10.t = 3600 – 5.t  15t = 3600
t = 3600/15  t = 240 s
dA = 10.t dA = 10 m/s x 240s
d = 2400 m de A

9. 7) Um corredor parte de um ponto com velocidade de 1,0 m/s; outro parte
da mesma posição, 20 s depois, com velocidade de 1,5 m/s. Quanto
tempo depois e em que posição eles se encontram?
RESOLUÇÃO
dA = vA.t  dA = 1,0.(t + 20)
dB = vB.t  dB= 1,5.t
No encontro  dA = dB , para calcular o tempo de encontro.
1,0.t + 20 =1,5.t  20 = 1,5t – 1,0t
t = 20/0,5  t = 40 s
dA = 10.(t + 20) dA = 1,0 m/s x (40s +20s)
d = 60 m do ponto de partida.

10. 8) Durante um nevoeiro, um navegador recebe dois sinais expedidos
simultaneamente por um ponto da costa, um deles através do ar e o outro
através da água. Entre as recepções dos dois sons, decorre um intervalo
de 5s. A velocidade do som, nas condições da experiência, tem valor de
330 m/s e 1320 m/s respectivamente no ar e na água. Pede-se a distância
entre o barco e o posto emissor dos sinais.
RESOLUÇÃO
dAr = vA.(t +5)  dAr = 330.t
dAguaA = vB.t  dAgua= 1320.(t – 5)
As distâncias são iguais,então vamos calcular o tempo percorrido
pelo som(dA =dAgua)
330.t = 1320.(t – 5)  330t = 1320.t - 6600
t = 6600/990  t = 6,67 s
dAr = 330.t  dAr = 330m/s x 6,67s
d = 2200 m

11. 9) Um trem de 120 m de comprimento percorre um trecho de ferrovia
retilínea com velocidade de 20 m/s. Um automóvel de comprimento
desprezível viaja no mesmo sentido com velocidade de 30 m/s.
Determine o tempo necessário para o automóvel ultrapassar o trem, a
partir do instante em que ele atinge a sua traseira. Admita velocidades
constantes para os móveis
RESOLUÇÃO:
vtrem = 20m/s
Vcarro = 30m/s
Considere v velocidade relativa entre o carro e o trem, então:
v = 30 – 20 = 10m/s, logo:
t =
d
v
=
120m
10m/s
 t =12 s

12. 10) Ao abrir o semáforo, um automóvel partiu do repouso
movimentando-se em linha reta, obedecendo ao gráfico ao lado. Após
20 s, o automóvel percorreu 280 m. Determine aceleração do carro, nos
primeiros 5 s.
RESOLUÇÃO:
d= área sob a linha do gráfico.
d = 280 m
d = Atriângulo+ Aretãngulo
𝑣.5
2
+ v.15 = 280
5v + 30.v = 560
35.v = 560  v = 16m/s
a =
Δ𝑣
Δ𝑡
=
16𝑚/𝑠
5𝑠
 a = 3,2m/s²

13. 11) Um automóvel parte do repouso com uma aceleração constante de
8m/s².
a) Que distância terá percorrido após 10 segundos de movimento?
RESOLUÇÃO:
d = v0.t + ½ a.t2
V0=0 (parte do repouso)
d = ½ a.t2 = ½ . 8m/s² . (10)²s² = 4.100 m  d= 400 m
b) Qual será sua velocidade após ter percorrido 1600 m?
RESOLUÇÃO:
v2 = v0
2 + 2.a.d
v2 = 0 + 2. 8.1600  v2 = 25.600  v = 160 m
c) Qual será sua velocidade média nos 10 primeiros segundos de
movimento?
RESOLUÇÃO:
v =
Δ𝑑
Δ𝑡
=
400𝑚
10𝑠
 v = 40 m/s

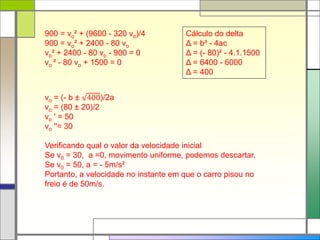
14. 12) Numa competição automobilística, um carro se aproxima de uma
curva em grande velocidade. O piloto pisa no freio durante 4s e
consegue reduzir a velocidade do carro para 30 m/s. Durante a freada, o
carro percorre 160m. Supondo que os freios imprimam ao carro uma
aceleração retardadora constante, calcule a velocidade do carro no
instante em que o piloto pisou no freio
RESOLUÇÃO:
v = 30m/s (é a velocidade final)
t = 4s
d = 160m
Cálculo da aceleração a = ΔV/t
a = (30 - vo)/4
Aplicando os dados na equação v² = vo² + 2.a.d
30² = vo² + 2.[(30 - vo)/4].160
900 = vo²+ 320.(30 - vo)/4

15. 900 = vo² + (9600 - 320 vo)/4
900 = vo² + 2400 - 80 vo
vo² + 2400 - 80 vo - 900 = 0
vo ² - 80 vo + 1500 = 0
Cálculo do delta
Δ = b² - 4ac
Δ = (- 80)² - 4.1.1500
Δ = 6400 - 6000
Δ = 400
vo = (- b ± 400)/2a
vo = (80 ± 20)/2
vo ' = 50
vo ''= 30
Verificando qual o valor da velocidade inicial
Se v0 = 30, a =0, movimento uniforme, podemos descartar.
Se v0 = 50, a = - 5m/s²
Portanto, a velocidade no instante em que o carro pisou no
freio é de 50m/s.

16. ESCOLA ESTADUAL
MAESTRO VILLA
LOBOS
• ELABORADO PROFa.
MONICA PEREIRA
RESOLUÇÃO DE EXERCICIOS
2016