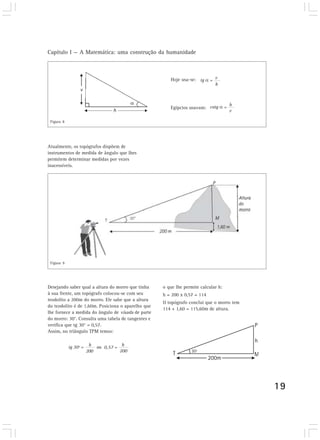
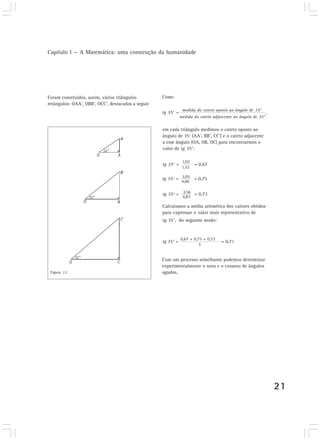
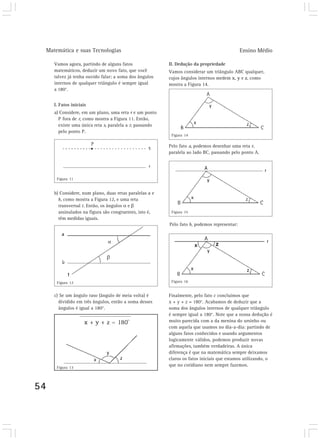
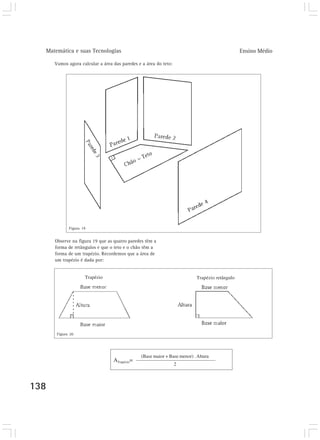
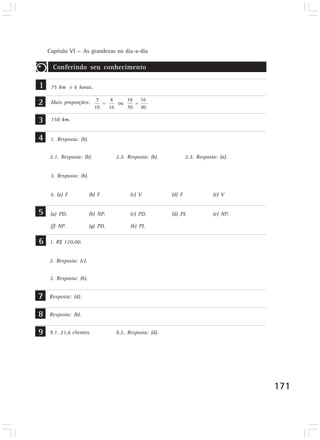
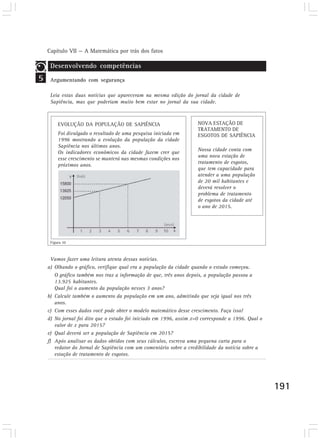
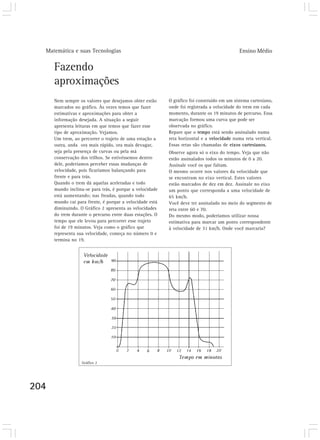
Este capítulo discute como a matemática surgiu como uma construção humana para resolver problemas do dia-a-dia relacionados à subsistência, e como foi se desenvolvendo e sofisticando ao longo do tempo para lidar com quantidades cada vez maiores. Também aborda como a linguagem matemática foi se desenvolvendo para permitir uma comunicação mais eficiente por meio de símbolos e representações.