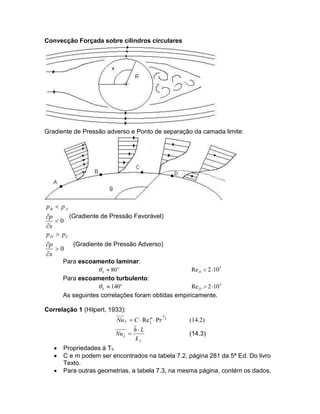
O documento apresenta conceitos e correlações para o cálculo de transferência de calor por convecção em escoamentos externos laminar e turbulento. São descritos os números de Nusselt, Reynolds, Prandtl e Schmidt, assim como correlações empíricas para geometrias como placas planas e cilindros circulares.

1. Escoamento Externo
Equivalente ao capítulo 7 do livro “Fundamentos de Transferência de Calor e
Massa”, Incropera & De Witt, 5ª Edição.
Introdução
Nesta parte, concentramos a atenção em problemas de convecção forçada
– onde a velocidade relativa entre o fluído e a superfície é mantida por meios
externos, como bombas, ventiladores, entre outros – a baixa velocidade e sem
mudança de fase.
O objetivo principal é determinar o coeficiente de convecção para diversas
geometrias de escoamento. Já foi visto anteriormente que, pela
adimensionalização das equações de camada limite, os coeficientes de convecção
local e médio podem ser correlacionados da seguinte maneira:
Para transferência de Calor:
Nu x  f x*, Re x , Pr 
Nu x  f Re x , Pr 
Nu x 
Para transferência de Massa:
hL
kf
Shx  f x*, Re x , Sc 
Shx  f Re x , Sc 

2. Correlações Empíricas
Com base em muitos resultados experimentais, verificou-se que:
 Nu l
log n
 Pr


  m  log Re L   log C


Nu l
 Re m  C
L
n
Pr
Nu L  C  Re m  Pr n
L
Onde:
Nu L = número de Nusselt médio (adimensional)
Re= número de Reynolds (adimensional)
Pr= número de Prandtl (adimensional)
C, m, n = constantes empíricas que dependem da geometria do problema e do
tipo de escoamento.
Pr 
   cp


kf
Re x 
 U   x

(13.6)

3. Escoamento Laminar
Apresenta solução analítica da camada limite:
v
5
(13.7)

x
Re x
A espessura da camada limite  v diminui com o aumento do Rex.
Da equação 13.7, temos:
 x 
Re x  25   
 
 v
Das equações 13.6 e 13.7, temos:
x
v  5
 U 
Escoamento Turbulento
v
0,37

x Re x  15
2
(13.8)
(13.9)
(13.10)
Exemplo:
Para L=0.1m,  v =2.3mm e ReL=106.
Da equação 13.10, temos:
 x
Re x  0,0069  

 v
De 13.6 e 13.10, temos:
1




5
(13.11)
4
  
5
 v  0,37  
(13.12)
  U   x

 

Das equações 13.8 e 13.11, verifica-se que, dentro da camada limite, o
número de Reynolds está relacionado à espessura da camada limite em cada
coordenada x.
Fora da camada limite, o número de Reynolds representa a razão entre as
forças de inércia (Fi) e as forças viscosas (Fv).
Forças de Inércia:
5
U 

  U 
  Volume
x 

2

U
Fi    

L


 A L


Forças Viscosas:
  2U 
   2   Volume

x 


 U 
Fv     2   A  L
L 


4. Razão entre Fi e Fv:
2
 U
 
L
Fi 

Fv  U 
  2
L


 A L



  U   L  Re L


 A L

(13.13)
Reynolds Crítico
O número de Reynolds crítico define Re acima do qual o escoamento deixa
de ser laminar e passa a ser turbulento. Seu valor depende de cada geometria.
Para placas planas, seu valor varia 105<Rec<106.
Número de Prandtl
Pr 
   cp


kf
Onde:
 =difusividade térmica (m2/s)


 =viscosidade cinemática   




cp=calor específico à pressão constante (J/Kg.K)
k=condutividade térmica (W/m.K)
Para o escoamento Laminar:
3
 
Pr   v 
 
 T
Isto é, o número de Prandtl é proporcional ao cubo da razão entre as
espessuras das camadas limites cinemática e térmica.
Exemplo:
Número de Prandtl

Razão V
T
Mercúrio
ar
água
Óleo
0,0248
0,707
5,8
6400
0,29
0,89
1,8
19
Para convecção de massa, existe um equivalente ao número de Prandtl:
Sc 

(número de Schmidt)
D AB
Onde: DAB= coeficiente de difusão binária de A em B.
Pode-se interpretar Prandtl como:
(Advecção de energia/difusão de energia)/(Forças de inércia/Forças viscosas)

5. (i)   c p  U  
  c p U  
T
L
(i )

(ii )
 2T
T
k 2
2
x
L
(ii) U   L
 
U  L 
T
L  U   L  Pe
T
L2
Pe  Re L  Pr
k

k
onde Pe= número de Pellet

Número de Nusselt
O número de Nusselt representa a razão entre as taxas de transferência de
calor por convecção e por condução no fluído.
Tsup  T
q cond  k  A 
q conv
T
sup
 T 
L
 h  A  Tsup  T qconv  h  A  Tsup  T 
q conv h  A  Tsup  T  h  L

Tsup  T   k f
q cond
k  A
L
h x
Nu x 
(13.17)
kf
Nu L 
hL
kf
Número de Sherwood (Sh)
Sh 
(13.18)
hm  L
D AB
hm  L
D AB
Onde: hm= coeficiente de transferência de massa
Sh 

6. Para o escoamento laminar:
1
1
h x
Nu x 
 0,332  Re 2  Pr 3
kf
(13.19)
hx  2  hx
(13.20)
Para o escoamento turbulento:
1. Para escoamento totalmente turbulento:
4
Nu x  0,0296  Re 5  Pr
4
1
Nu x  0,037  Re 5  Pr 3
Limites de Validade destas correlações:
0,6  Pr  60
1
3
(13.21)
(13.22)
Re x  10 8
2. Para escoamento misto (laminar + turbulento):
4
1
Nu x   0,037  Re 5  871  Pr 3




Para encontrar o ponto de transição:
  U   xcrit
Re critico 
 5  10 5

Temperatura de filme (Tf)
Para usar as correlações vistas, as propriedades do fluído (massa
específica, viscosidade, calor específico, condutividade térmica, etc.) devem ser
avaliadas à Tf, tal que:
 Tsup  T 

Tf  


2


Outras correlações são apresentadas na seção 7.2 do livro texto.
Metodologia para cálculos de convecção
1. Reconhecer a geometria
2. Identificar a Temperatura adequada às propriedades do fluído
3. Calcular Re e determinar o tipo de escoamento
4. Selecionar a correlação apropriada e obter (Nu, Sh) e (h, hm)
5. Calcular q ou  A

7. Convecção Forçada sobre cilindros circulares
Gradiente de Pressão adverso e Ponto de separação da camada limite:
pB  p A
(Gradiente de Pressão Favorável)
p
0
x
p D  pC
p
0
x
(Gradiente de Pressão Adverso)
Para escoamento laminar:
Re D  2 105
 S  80 o
Para escoamento turbulento:
 S  140o
Re D  2 105
As seguintes correlações foram obtidas empiricamente.
Correlação 1 (Hilpert, 1933):
Nu L  C  Re m  Pr
L
Nu L 



hL
kf
1
3
(14.2)
(14.3)
Propriedades à Tf.
C e m podem ser encontrados na tabela 7.2, página 281 da 5ª Ed. Do livro
Texto.
Para outras geometrias, a tabela 7.3, na mesma página, contém os dados.

8. Correlação 2 (Churchill e Bernstein, 1977):
1
Nu D  0,3 


0,62  Re D2  Pr
  0,4 
1  

  Pr 

Propriedades a Tf.
Red.Pr > 0,2
2
3




1
1
3
4
  Re  5 8 
D
 1  
 
  282000  


4
5
(14.4)
Correlação 3 (Zhukauskas, 1972):
1
 Pr  4

Nu L  C  Re  Pr  
 Pr 
 sup 
Propriedades a T exceto Prsup (a Tsup)
Incerteza do número de Nusselt maior que 20%.
m
L


n
(14.5)
Convecção forçada sobre esferas
Correlação empírica de Whitaker (1972):
2
2   
1

Nu D  2   0,4  Re D2  0,06  Re D3   Pr 5  


 


 sup 
Condições:
0,71<Pr<380
3,5<Red<7,6.104
  
 <3,2
1,0< 
 
 sup 
 Propriedades avaliadas a T , exceto sup .
1
4
(14.6)