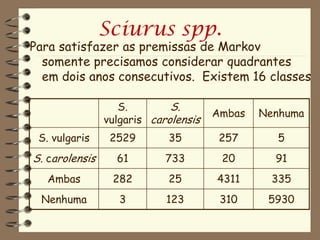
O documento discute três tópicos principais: (1) cadeias de Markov para modelar o estado de humor de Gladys, (2) cadeias de Markov de quatro estados para modelar as condições meteorológicas, (3) uso da matriz de Leslie para modelar populações com estrutura etária, como as populações de esquilos Sciurus no Reino Unido.

1. Ecologia de Populações

2. Estado de Espírito
Em qualquer dia, Gladys é alegre (A), normal (N),
ou chata (C).
– Se ela está A hoje, então estará N, A ou C amanha
com probabilidades respectivas de 0.5, 0.4, 0.1.
– Se ela está N hoje, então ela estará C, A, ou N
amanha com probabilidades de 0.3, 0.4, 0.3.
– Se ela está C hoje, então ela estará A,N ou C
amanha com probabilidades de 0.2, 0.3, 0.5.
4 Representamos o estado de espírito de Gladys
no dia n como Xn
– Então { Xn , n ≥ 0} é uma cadeia de Markov de três
estados

3. Tempo
Se chova ou não depende do tempo dos últimos
dois dias
– Se choveu durante os últimos dois dias, então existe
uma probabilidade de 0.7 de que choverá amanhã
– Se choveu hoje, mas não ontem, então existe uma
probabilidade de 0.5 de que choverá amanhã
– Se choveu ontem, mas não hoje, então existe uma
probabilidade de 0.4 de que choverá amanhã
– Se não choveu durante os últimos dois dias, então
existe uma probabilidade de 0.2 de que choverá
amanhã

4. Tempo
Se o estado no tempo n depende somente de se
chova ou não no tempo n, então não é uma
cadeia de Markov
– Por que nãot?
4 Mas podemos fazer uma cadeia de Markov se
consideramos 4 estados (determinados pelas
condições meteorológicas de hoje e ontem)
Estado 0 Se choveu hoje e ontem
Estado 1 Se choveu hoje mas não ontem
Estado 2 Se choveu ontem mas não hoje
Estado 3 Se não choveu nos dos dias

5. Tempo
Agora existe uma cadeia de Markov de 4 estados
Somente precisamos escrever a matriz de
probabilidades de transição
Estado 0 Se choveu hoje e ontem
Estado 1 Se choveu hoje mas não ontem
Estado 2 Se choveu ontem mas não hoje
Estado 3 Se não choveu nos dos dias

6. Sciurus spp.
Sciurus carolensis
– Introduzido na Grão Bretanha numa
serie de solturas em várias localidades desde 1876
– Agora ocupa a Inglaterra e Gales e parte de Escócia
e Irlanda
Sciuris vulgaris
Com uma subespécie endêmica
– Agora não esta presente na maioria
das áreas colonizadas por S. carolensis
– No último século a população caiu drasticamente e
continuamente
• Extinta em muitas partes de Inglaterra e Gales
• Algumas populações ainda existem em ilhas marítimas no sul
de Inglaterra e nos montanhas de Gales

7. Sciurus spp.
• Introduções de S. carolensis duraram ate 1920
• Em 1930 foi considerada como praga as florestas
decíduas e medidas de controle foram tentadas
• Levantamentos nacionais de distribuição foram
realizados
• Encontraram que S. vulgaris estava sumindo das áreas
colonizadas por S. carolensis durante os últimos 15 a
20 anos
• Questionários foram preenchidos por engenheiros
florestais sobre as populações de Sciurus
– Mudanças na abundancia de Sciurus, danos as árvores,
medidas de controle, e o número de Sciurus mortos

8. Sciurus spp.
• Com esses dados podemos fazer um modelo
para prever a tendência na distribuição das
espécies na Grão Bretanha
• Usher et al
– Técnicas de sobreposição foram usadas para
extrair dados dos mapas de distribuição da
comissão florestal
– Os mapas foram dividido em quadros de 10km
– Cada quadro de 10km foi classificado como
• somente S. vulgaris registrada no ano
• somente S. carolensis registrada no ano
• ambas espécies presentes
• nenhuma espécie presente

9. Sciurus spp.
Para satisfazer as premissas de Markov
somente precisamos considerar quadrantes
em dois anos consecutivos. Existem 16 classes
S. S.
Ambas Nenhuma
vulgaris carolensis
S. vulgaris 2529 35 257 5
S. carolensis 61 733 20 91
Ambas 282 25 4311 335
Nenhuma 3 123 310 5930

10. Sciurus spp.
O que acontece as populações de Sciurus
num período grande de tempo?

11. Populações com
Estrutura Etária

12. Populações com Estrutura Etária
4 Populações com gerações que não
sobrepõem
4 Pode existir problemas de várias
gerações previas ou a distribuição
etária inteira
4 Geralmente sua resolução é pelo uso daa
matriz de Leslie, desenvolvido por P.H.
Leslie (1945)
4 Representamos o número de indivíduos
de idade de i no ano, ou geração, t como
xit

13. Populações com Estrutura Etária
4 xit é o número de indivíduos de idade de i em
ano, ou geração t
pi  Pr(que um indivíduo da idade i no ano t
sobrevive até o ano t  1)
mi  número médio de proles produzidas por
indivíduos de cada idade i
4 Os recém nascidos tem idade de 0
4 A idade máxima é w
4 Se estamos modelando uma espécie sexual
somente consideramos o número de fêmeas e
recém nascidos
– Tem a premissa que há machos suficientes

14. Matriz de Leslie
A “Fecundidade bruta” de indivíduos de
idade de i = mip0
– (quantos filhotes)(quantos sobrevivem
(probabilidade))
– Número de indivíduos de idade de 1 na classe t+1
por indivíduo de idade de i no tempo t
Então
xi ,t 1  pi 1 xi 1,t para i  2,3,..., w
w
x1,t 1   p0 mi xi ,t
i 1

15. Matriz de Leslie
 x1,t 
A matriz de Leslie   x 
xt   2 ,t 
  
 
 x w ,t 
 p0 m1 p0 m2 p0 m3 ... p0 mw1 p0 mw 
 p 0 0 ... 0 0  
 1
L 0 p2 0 ... 0 0 
 
       
 0
 0 0  pw1 0  

16. Matriz de Leslie
Então  
xt 1  xt L
Nunca chega a x0 com essa formulação
É um processo de Markov?
– Não! As i,j’s são transpostas de forma que Lij da
a contribuição xi de xj
• Também, as somas das colunas refletiam o número de
indivíduos na geração t+1 por indivíduo de idade de j em
t
• A soma não precisa ser =1 (diferente dos processos de
Markov, que são conservativos

17. Matriz de Leslie
Muitas premissas ficam escondidas
– Somente a idade é o predito dominante da
probabilidade de fecundidade e sobrevivência
– (ignora qualquer efeito do tamanho total da
população)
– Mais outras premissas
Analogamente com as cadeias de Markov 
podemos solver a distribuição estável de X
idades x
X i  lim t  w
i ,t
x
i 1
i ,t

18. Matriz de Leslie
4 Analogamente as cadeias de Markov podemos
resolver a “distribuição estável de idades”
xi ,t
X i  lim t  w
x
i 1
i ,t
– Proporção da população total da idade de i
4 Se a distribuição etária é estável, então
 
LX  X para algum escalar 

19. Matriz de Leslie

4 So,
X é um eigenvetor de L
4 Se L tem um eigenvalor  dominante único e
real eigenvalor que corresponde ao eigenvetor

direto para X então para t1 de tamanho
suficiente
 
 Lx0  x1
     2
Lt1 x0  cX  x2  Lx1  LLx0  L x0
  n
 xn  L x0
4 É a distribuição estável de idades

– x a distribuição estável de idades
t1

20. Matriz de Leslie
Para   t t1 t1  t t1

t  t1 : xt  L x0  L L x0  cL X
t
 
LX  X
Mas,
 
Então xt  c1 X
t
A distribuição no tempo t é dada pela distribuição
estável de idades escalonada por t e c1
Se >1, todas as classes de idade e a população total
cresceram geometricamente por  a cada ano, mas a
distribuição das idades não muda

21. Matriz de Leslie
4 Isso é somente verdadeiro para t>t1 (até atingir
a distribuição estável de idades)
4 Mas o que é c1?

– Se  é um vetor de fila dado pelo eigenvetor
 
esquerdo  de L ( L= onde  é o eigenvalor) com

escala de forma que  x=1
  
– Agora x  Lt x  c t X
t 0 1
 t  t
 L x0   c1 X
 t  
  x0  c1  X
t
mas  X  1

 x0  c1

22. Matriz de Leslie
 
Dado L, podemos resolver para , X ,  , então

x0 dado que conhecemos c1
4 Dado a distribuição estável de idades, a
quantidade que a população muda cada ano ()

podemos calcular a distribuição atual xt para
qualquer t

4 O que é  ?

–  da a importância relativa dos indivíduos de
idades diferentes em x0 ao tamanho futuro da
população

23. Matriz de Leslie
Exemplo

– Se  =[1 1.6 1.4 1.3]/|X|
– Significa que um indivíduo de dois anos de idade no tempo 0
teria 1.6 vezes mais filhotes (descendentes) no futuro
distante como um indivíduo de um ano de idade no tempo 0
“Eu achei que as condições iniciais não afeita a
distribuição a largo prazo”
– Verdadeiro para processos de Markov de conjunto fechado,
aperiódico e irreduzível
– Para esses processos de Markov, o número total de indivíduos
é constante
– Mas com a Matriz de Leslie, as counas geralmente não somem
a1
• A população pode aumentar no tempo

24. Probabilidade de Sobrevivência
Se i=p0p1p2…pi-1 seja a probabilidade de que um
recém nascido sobrevive até a idade de i
– Lembre que xi,t= número de indivíduos de idade de i
na geração no tempo t
– Os recém nascidos na geração t podem ser escrito
w onde mi  número de proles por indivíduo de idade i
x0,t   xi ,t mi
i 1 e w é a idade maior
Os indivíduos de idade de i na geração t que
nascerem em t-i e sobreviveram
xi ,t  x0,t i i

25. Probabilidade de Sobrevivência
Ao atingir a distribuição estável de idades, cada
grupo aumenta geometricamente a taxa 
x 
i ,t 1
i
 x0,t
xi ,t 1   x0,t i
xi ,t 1 i   x0,t  i
i
xi ,t   x0,t  i
i
O número de idade de i no tempo t em termos
do número de recém nascidos em t

26. Probabilidade de Sobrevivência
Se alcançamos uma distribuição estável de idades,
cada classe de idade aumenta geometricamente por

x 
0 ,t  i
i
x0 ,t
x0,t i   x0,t
i
x0,t i i   x0,t  i
i
xi ,t   x0,t  i
i
Número de indivíduos de idade de i no tempo t em
termos do número de recém nascidos no tempo t

27. Probabilidade de Sobrevivência
Então,
w
x0,t   i x0,t  i mi
i 1
w
o que resulta em  i i mi  1
i 1
A partir disso podemos calcular explicitamente
