O documento apresenta um plano de aula com atividades focadas na compreensão e desenvolvimento de expressões algébricas. Inclui exercícios práticos, discussões sobre diferentes métodos de resolução e desafios para aplicar conhecimentos matemáticos relacionados a monômios e polinômios. Ao final, são destacadas as formas reduzidas e desenvolvidas das expressões, enfatizando a equivalência e a importância do pensamento algébrico.

1. Atividades Objetivo principal Ação principal Tempo
sugerido
Retomada
Relembrar a ideia da função do monômio
e polinômios, (parte literal e coeficiente
numérico) nas expressões algébricas.
Retomar a ideia da função do monômio e
polinômios, (parte literal e coeficiente
numérico) nas expressões algébricas.
7 min.
Atividade
Explorar o desenvolvimento e
generalização das expressões algébricas
Reconhecer e explorar o desenvolvimento e
generalização das expressões algébricas
18 min.
Discussão de
soluções
Apresentar as diferentes formas de
resolução, reconhecendo as expressões
algébricas na forma reduzida.
Acompanhar passo a passo as diferentes
estratégias encontradas e discutir os
procedimentos.
14 min.
Encerramento Sistematizar as aprendizagens da aula.
Ler a aprendizagem da aula e evidenciar os
conhecimentos.
3 min.
Raio X
Verificar a aplicação dos conhecimentos
adquiridos em situação semelhante e
avaliar os conhecimentos.
Resolver utilizando o conhecimento
apreendido.
6 min

2. Objetivo: Reconhecer e explorar o desenvolvimento e a
generalização das expressões algébricas.

3. Você sabe o que são expressões algébricas?
As expressões algébricas são contas com letras e números.
Isso mesmo, as expressões algébricas são formadas por
uma parte literal, um coeficiente numérico e uma
operação. Como, por exemplo: 2xy, em que 2 é o
coeficiente numérico e xy a parte literal.
A expressão algébrica 3x + 2y pode ser escrita como
x + x + x + y + y?
Sim, neste caso temos a expressão algébrica simplificada e
a expressão algébrica desenvolvida, respectivamente. Vale
lembrar que só podemos somar monômios semelhantes,
em que a parte literal é semelhante.

4. Você é um bom detetive?
Nesta série de seis desafios vamos testar seus conhecimentos, sua
concentração e habilidades matemáticas.
Neste jogo você deve desenvolver as expressões algébricas, e depois
conferir com seus colegas. Quem tiver mais acertos será o campeão.
Vamos lá!!
Desafio 1 Desafio 2
4. (r2 + 2r -3) (x + 7) (y - 3)
Desafio 3 Desafio 4
(3b +7)2 + 2 (9 - 2k)2 + 6
Desafio 5 Desafio 6
(2a + 3).(2a - 3). 7 (7m +2n)3 + (7m -2n)3

5. Marque na tabela a seguir O para acertos e x para os erros:
Para desenvolver as expressões algébricas dos desafios anteriores, você
utilizou seus conhecimentos de:
● Propriedade distributiva da multiplicação em relação à adição;
● Quadrado da Soma;
● Quadrado da Diferença;
● Diferença de dois Quadrados;
● Cubo da Soma;
● Cubo da Diferença.
Você consegue generalizar a expressão algébrica desenvolvida de cada
um desses conceitos?
Desafio 1 Desafio 2 Desafio 3 Desafio 4 Desafio 5 Desafio 6
O x O x O x O x O x O x

6. Propriedade distributiva da multiplicação em relação à adição
Desafio 1 4. (r2 + 2r -3)
4.r2 + 4.2r - 4.3
4r2 + 8r - 12
4. (r2 + 2r -3)
Desafio 2 (x + 7) (y - 3)
x.y - 3.x + 7.y - 3.7
xy - 3x + 7y - 21
(x + 7) (y - 3)
Quadrado da Soma
Desafio 3 (3b +7)2 + 2
(3b)2 + 2.3b.7 + 72 + 2
9b2 + 42b + 49 + 2
9b2 + 42b + 51
(3b +7)2 + 2

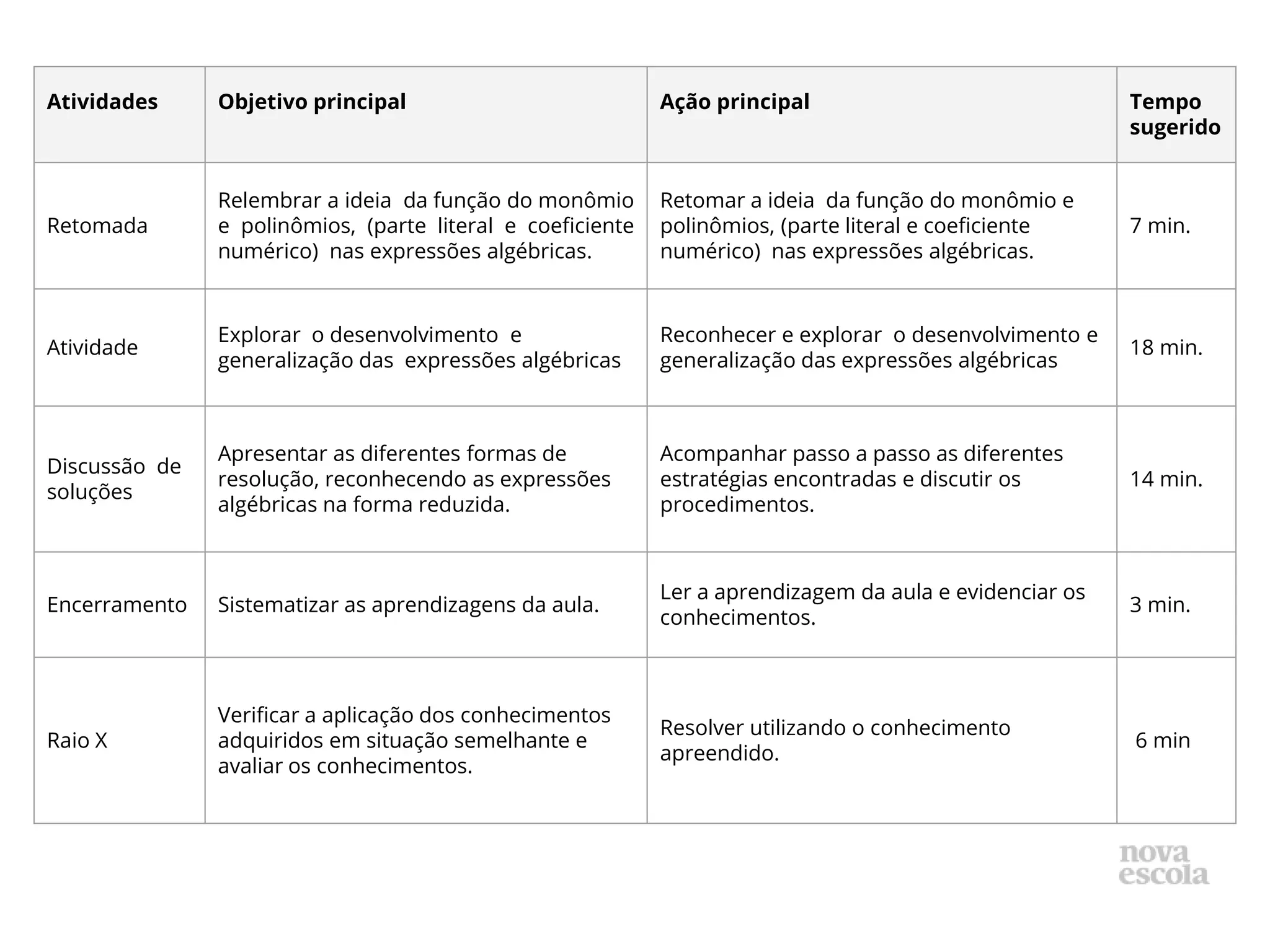
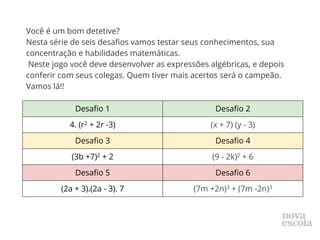
7. Quadrado da Diferença
Desafio 4 (9 - 2k)2 + 6
92 - 2.9.2k + (2k)2 + 6
81 - 36 k + 4k2 + 6
4k2 -36k + 87
(9 - 2k)2 + 6
Diferença de dois Quadrados
Desafio 5 7.(2a.2a -2a.3 + 3.2a - 3.3)
7.[(2a)2 - 32]
7.(4a2 - 9)
28a2 - 63
7.(2a + 3).(2a - 3)
Cubo da Soma e Cubo da Diferença - Desafio 6
(7m +2n)3 + (7m -2n)3
(7m)3 + 3.(7m)2.2n + 3.7m.(2n)2 + (2n)3 + (7m)3 - 3.(7m)2.2n + 3.7m.(2n)2 - (2n)3
(7m)3 + (7m)3 + 3.(7m)2.2n - 3.(7m)2.2n + 3.7m.(2n)2 + 3.7m.(2n)2 + (2n)3 - (2n)3
343m3 + 343m3 + 84mn2 + 84mn2
686m3 + 168mn2

8. Propriedade distributiva da multiplicação em relação à adição
a. (b + c) a.b + a.c
(a + b).(c + d) a.c + a.d + b.c + b.d
Quadrado da Soma
(a + b)2 a2 + 2ab +b2
Quadrado da Diferença
(a - b)2 a2 - 2ab +b2
Diferença de dois Quadrados
(a + b).(a - b) a2 - b2
Cubo da Soma
(a + b)3 a3 + 3a2b + 3ab2 + b3
Cubo da Diferença
(a + b)3 a3 + 3a2b + 3ab2 + b3

9. Nesta aula aprendemos que as
expressões algébricas podem ser escritas de
formas variadas - na forma reduzida e na
forma desenvolvida, e apesar de
aparentemente diferentes, essas expressões
algébricas são equivalente.
E ao abstrair e generalizar a expressão,
desenvolvemos capacidades relacionadas ao
pensamento algébrico, pois ao utilizarmos a
linguagem algébrica podemos representar as
conjecturas e justificando a sua validade para
qualquer número.

10. Identifique a coluna de expressões algébricas reduzidas ou
desenvolvidas, e complete as lacunas na tabela:
Expressão algébrica _______________ Expressão algébrica _______________
3.(5x + __y) __x + 21y
(6 + __)2 ___ + ___a + a2
(___ - __)2 4b2 - ______ + 64
(7 + 2s).(7 - ___) ____ - 4s2
(___ - 2t)3 64 - ____ + 48t2 - ____