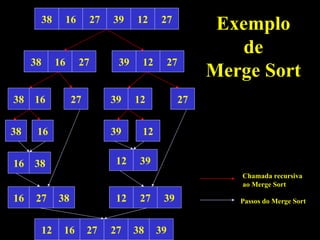
O documento resume dois algoritmos de ordenação: merge sort e bin sort. O merge sort é um algoritmo recursivo que ordena dividindo o array ao meio e ordenando recursivamente cada metade, e depois intercalando as partes ordenadas. Sua complexidade é O(n log n). O bin sort utiliza um vetor auxiliar para contar a frequência de cada elemento e ordenar em uma única passagem, tendo complexidade O(k*n log n).

1. Discentes: Eduardo Dal Molin Kleber Berhend Willian (ED) Métodos de Ordenação

3. Exemplo de Merge Sort 38 16 27 27 12 39 27 38 16 27 39 12 38 16 27 39 12 27 38 16 39 12 38 16 39 12 38 16 27 39 12 27 12 16 27 27 38 39 Chamada recursiva ao Merge Sort Passos do Merge Sort

4. Vantagens e Desvantagens

6. Implementação em C Void merge (int M[5o], int inicio, int fim) { int meio; comparações[3]++; if (inicio < fim) { meio = ((inicio + fim)/2); merge (M, inicio, meio); merge (M, meio+1, fim); intercala (M, inicio, meio, fim); } }

7. void intercala (int M[50], int inicio, int fim) { int primeiro, res, segundo, k; int C[]50; primeiro = res = inicio; segundo = meio + 1; while (primeiro <= meio && segundo <= fim) { comparacoes[3]++; if (M[primeiro] <= M[segundo]) { atribuicoes [3]++; C[res]= M[primeiro]; primeiro++; }

8. else { atribuicoes[3]++; C[res] = M[segundo]; segundo++; } res++; } comparacoes[3]++; if (primeiro > meio) for (k=segundo; k<=meio; k++) { atribuicoes[3]++; C[res] = M[k]; res++; }

9. else for (k=primeiro; k<=meio; k++) { atribuicoes[3]++; C[res] = M[k]; res++; } for (k=inicio; k<=fim; k++) M[k] = C[k]; }

10. BIN SORT

12. Exemplo 3 2 1 3 3 2 -1 2 3 -1 -1 1 -1 -1 -1 1 2 3 Aux[2] Aux[1] Aux[0] X[2] X[1] X[0] Varredura

14. Implementação #define n ‘k’-’a’ +1; Void binsort(apitem *lista , int size){ apitem v[n]; for(i = 0; i < n; i ++) v[i] = NULL; for(i = size - 1; i > = 0; i --){ while((p = removefirst(lista))!= NULL) insert (p ,&v[p -> info[i] – ‘a’); for(j = 0;j > n; j ++) concat(lista,&v[j]); } }

15. . (próximo slide). FIM DO THE END