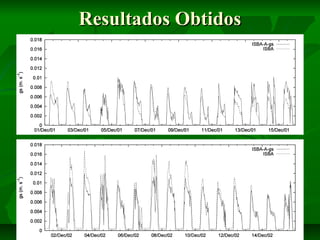
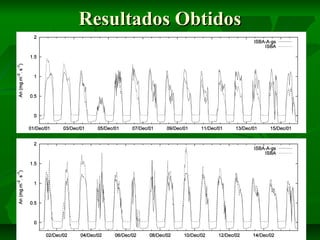
Este documento descreve um estudo sobre a quantificação do fluxo de CO2 emitido pela vegetação inundada pela formação de represas. O documento apresenta o modelo ISBA-A-gs, que acopla o modelo ISBA com a rotina A-gs para descrever os processos fisiológicos nas folhas e calcular o fluxo de CO2. Os dados meteorológicos de duas séries temporais são utilizados como entrada para o modelo.

1. UNIVERSIDADE FEDERAL DO PARANÁ
CURSO DE ENGENHARIA AMBIENTAL
DISCIPLINA: PROJETO DE FINAL 2
FLUXO DE CO2 DE VEGETAÇÃO
INUNDADA POR REPRESAMENTO –
QUANTIFICAÇÃO PRÉ ALAGAMENTO

2. Resumo





Estudos recentes indicam que lagos de usinas Hidrelétricas
emitem quantidades significativas de gases de efeito estufa.
Para quantificar a quantidade liberada para a atmosfera é
necessário quantificar também o fluxo de gás carbônico da
vegetação que ali estava anteriormente ao represamento.
Este trabalho descreve um método para calcular o fluxo de gás
carbônico utilizando o modelo de interação superfícievegetação-atmosfera ISBA de Noilhan e Planton (1989);
Noilhan e Mahfouf (1996).
Foi acoplado a rotina A-gs baseado em Jacobs (1994); Jacobs et
al. (1996) para descrever os processos fisiológicos na escala das
folhas.
Este modelo apresentado em Calvet et al., (1998); Calvet,
(2000) foi denominado ISBA-A-gs.

3. Introdução




As hidrelétricas emitem gases de efeito estufa, bem como os
absorve também. A questão agora é quantificar corretamente estas
emissões.
Para isto é necessário a verificação de vários fluxos, dentre eles a
assimilação e emissão de gás carbônico da vegetação que existia
no local antes do alagamento.
Os lagos tradicionalmente têm sido considerados com produção
primária excedendo a respiração bacteriana, funcionando como
sumidouro de carbono. Entretanto, estudos têm demonstrado que
muitos lagos funcionam como fontes de dióxido de carbono para
atmosfera.
Para a vegetação anterior ao alagamento, a fotossíntese e a
respiração, atuam como sumidouro e fonte de dióxido de carbono
para a atmosfera. O balanço entre esses dois processos é
designado balanço de dióxido de carbono do ecossistema.

4. Introdução





Os estômatos são as estruturas existentes nas folhas das plantas
que permitem a passagem do CO2 da atmosfera para o interior da
planta e vice-versa. Simultaneamente permitem a saída de água
para a atmosfera.
Estudos sobre mudanças no uso do solo e suas consequências para
o clima necessitam de monitoramento contínuo de grandezas
meteorológicas, hidrológicas e fluxos superfíciais.
Medições rotineiras de fluxos superficiais requerem muito
esforço.
Monitoramento contínuo dos fluxos superficiais de massa e
energia através de sistemas confiáveis capazes de gerar séries de
longa duração é uma importante ferramenta para o estudo e a
quantificação das interações superfície-atmosfera.
A rotina A-gs (Jacobs, 1994; Jacobs et al. 1996) descreve os
processos fisiológicos na escala das folhas calculando a

5. Introdução



condutância dos estômatos através de parâmetros físicos e
biológicos, levando em consideração a assimilação líquida de gás
carbônico pelas folhas.
Neste trabalho foi acoplado ao modelo ISBA (Noilhan e Planton
1989; Noilhan e Mahfouf 1996) a rotina A-gs.
Utilizando o modelo ISBA-A-gs (Calvet et al. 1998; Calvet 2000)
e o ISBA original, pretende-se calcular o fluxo de gás carbônico
em uma vegetação anteriormente ao seu inundamento, utilizando
parâmetros da vegetação e solo que ali existiam e forçantes
medidos em estações meteorológicas da região no período
desejado.
Os dados prognósticos do modelo ISBA-A-gs serão comparados
com a saída do modelo ISBA original.

6. Dados Utilizados





Foram medidos em uma superestação experimental instalada na
Fazenda São Lourenço em Santa Terezinha do Itaipu, no oeste do
Estado do Paraná.
Duas séries de dados foram analisadas nesta pesquisa. A primeira
de 15/02/2001 até 22/02/2002 e a segunda de 20/03/2002 até
31/12/2002.
Necessário definir qual a vegetação havia anteriormente ao
represamento e de que represa. Foi suposto didaticamente uma
vegetação inundada pela represa de Itaipu.
Constatado que nesta região não existe mais floresta nativa e a
vegetação predominante são as culturas agrícolas, dentre as várias
culturas agrícolas existentes, foi escolhida a soja.
Os dados originais foram convertidos em duas séries menores que
compreendem os períodos da safra da soja, de 01/10/2001 até
31/01/2002 e 01/10/2002 até 31/12/2002. Estas duas séries foram
definidas neste trabalho como A e B respectivamente.

7. Modelo ISBA original


O modelo ISBA original de Noilhan e Planton (1989) utiliza
dados de temperatura do ar, umidade relativa do ar, velocidade do
vento, precipitação, radiação solar incidente e refletida. Particiona
as variáveis com balanços de energia e umidade na interface
Terra-Atmosfera e integra as equações diferenciais ordinárias no
tempo para prever as temperaturas e umidades desejadas.
Esquema e variáveis do modelo:

8. Modelo ISBA original

Equações diferenciais ordinárias:
∂Ts
2π
= CT ( Rn − H − LE ) −
(Ts − T2 )
∂t
τd
∂T2 1
= (Ts − T2 )
∂t τ d
∂Wg
C1
C2
=
( Pg − Eg ) − (Wg − Wgeq )
∂t
ρ w d1
τd
∂W2
1
=
( Pg − Eg − Etr )
∂t
ρ wd 2
∂Wr
1
=
[ Pr − ( Ev − Etr ) − Rr ]
∂t
ρwd r

9. Modelo ISBA original





A seguir cada parâmetro do modelo é apresentado.
1
Coeficiente térmico: C =
T
1 − veg veg
+
CG
CV
Rn = ( Rsi − Rsr ) + ε aσTa4 − ε gσTs4
Radiação Líquida:
Fluxo de Calor Sensível: H = ρc p Cdh Va (Ts −Ta )
Fluxo de Calor Latente: LE = L( E g + Ev )
 Evaporação do solo: E = (1 − veg ) ρ C V [ h q
g
a dq a u vsat (Ts ) − qva ]
 Evapotranspiração: pode ser um fluxo negativo e positivo.
No primeiro caso ocorre condensação do ar na superfície das
folhas: E v = veg ρa C dq Va [ q vsat ( Ts ) − q va ]
No segundo o fluxo de umidade é da vegetação para a
atmosfera: Ev = Etr + Er

10. Modelo ISBA original
 1 − Fw 
Etr = veg ρ a 
 R + R [ qvsat ( Ts ) − qva ]

s 
 a
 Fw 
Er = veg ρa  [ qvsat ( Ts ) − qva ]
R 
 a




Rs min
Rs =
Resistência estomática:
LAI F1 F2 F3 F4
Influência da fotossíntese (F1), pressão hidráulica induzida por
diferença de umidade no solo (F2), pressão de vapor na atmosfera
(F3) e temperatura do ar na resistência estomática (F4).
Precipitação interceptada pela vegetação: Pr = veg P
Precipitação que atinge o solo: Pg = (1 − veg ) P + Rr
Escoamento superficial na vegetação:
ρw d r
Rr = (Wr −Wr max )
∆t

11. Modelo ISBA original

Solo:
 Wsat
C1 = C1sat 
W
 g





b
+1
2

W2
C2 = C2 ref 
W −W +W
2
l
 sat




Vegetação:
Foi inserido o parâmetro LAI e veg da seguinte maneira: no mês
de outubro encerra-se o cultivo da safra de milho e resta apenas
palhas secas cobrindo a área de estudo (LAI=0,01 e veg=0,91), em
novembro a soja plantada começa a brotar (LAI=1 e veg=0,1), em
dezembro a cultura se encontra em crescimento com alturas entre
40-70 cm (LAI=2 e veg=0,7) e em janeiro com pleno
desenvolvimento (LAI=3 e veg=0,9).

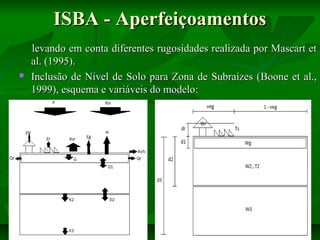
12. ISBA - Aperfeiçoamentos


Parametrização para Climas Tropicais Chuvosos: Cv suposto igual
a 2.10-5 Km2/J (Manzi e Planton, 1994).
Drenagem Gravitacional (Mahfouf e Noilhan, 1996):
A equação para W2 do modelo ISBA torna-se:
[
C3
∂W2
1
( Pg − Eg − Etr ) − max 0, (W2 − W fc )
=
∂t
ρw d2
τd


Escoamento Superficial (Habets et al., 1999):
P − (Wsat − W2 ) he


 Pref − P 

Qr = P − (Wsat − W2 ) he + 
 (W − W ) 

wilt 
 sat


0

]
se
P > Pref
se
0 < P ≤ Pref
se
P =0
Coeficiente de Transporte de Escalares: baseado no
desenvolvimento de Businger et al. (1971), corrigidos por Dyer

13. ISBA - Aperfeiçoamentos

levando em conta diferentes rugosidades realizada por Mascart et
al. (1995).
Inclusão de Nível de Solo para Zona de Subraízes ( Boone et al.,
1999), esquema e variáveis do modelo:

14. ISBA - Aperfeiçoamentos

A equação para a variação da umidade do solo na segunda camada
recebe duas novas variáveis D2 e K2 e é adicionada uma nova
equação para a variação da umidade nesta nova camada:
∂W2
1
=
( Pg − E g − Etr ) − D2 − K 2
∂t
ρwd 2
∂W3
d2
=
(K 2 + D 2 ) − K3
∂t
d3 − d 2

15. Variáveis do Modelo ISBA

Forçantes: temperatura atmosférica (Ta), Radiação solar incidente
e refletida (Rsi, Rsr), umidade relativa do ar (ya), velocidade do
vento (Va) e precipitação (P).

Prognósticas: fluxos de calor, temperatura e umidade do solo e
radiação líquida na superfície (Rn , G , H , LE , Ts , T2 , Wg , W2 , W3
, Wr).

16. Modelo A-gs


Plantas C3: têm como primeiro produto da fixação de CO2 um
composto com três carbonos, abrangendo aquelas plantas que
possuem somente a enzima Rubisco, pertencente ao Ciclo de
Calvin, como alternativa para a fixação do carbono. A reação de
carboxilação da Rubisco resulta na produção de duas moléculas
idênticas, do mesmo composto de três carbonos (o ácido 3-fosfoglicérico).
Nos modelos SVAT atuais, calcular valores realistas da
condutância do estômato vem sendo a chave da questão para
melhores estimativas do balanço de energia e carbono. A maioria
dos modelos são dos dois tipos descritos a seguir: o primeiro
grupo descreve a condutância do estômato como produto de
funções (Jarvis, 1976), sendo que cada função representa o efeito
de uma variável do meio, desta maneira, supõem-se que os fatores
envolvidos atuam independentemente na abertura dos estômatos.

17. Modelo A-gs


No segundo grupo de modelos chamados A-gs, a resposta da
assimilação fotossintética líquida (An) aos fatores ambientais é
modelada separadamente e através de seu valor é calculada a
condutância nos estômatos (Collatz, 1991).
A aproximação A-gs (Jacobs, 1994; Jacobs et al. 1996) é usada
para descrever os processos fisiológicos nas escalas das folhas no
ISBA-A-gs (Calvet et al., 1998; Calvet, 2000), no qual este
trabalho se baseou.
Baseado no fato de que a difusão do vapor d’água para fora da
folha e a absorção do CO2 utilizado para a fotossíntese ocorrem
pelo mesmo caminho, pode-se definir gs da seguinte maneira:
1,6 An
gs =
C s − Ci

18. Modelo A-gs

Resposta dos Parâmetros a Temperatura:
A dependência da temperatura na fotossíntese é computada
através de Γ, gm e Am,max. A resposta da temperatura destas variáveis
é baseada em uma função resposta Q10, a qual é definida como o
crescimento proporcional de um valor parâmetro ao crescimento
de 10 graus Celsius na temperatura (Berry e Raison, 1982).
T − 25
10
10
X (T ) = X (at 25)Q
T − 25
10
10
X (at 25)Q
X (T ) =
{1 + exp[0,3(T1 − T )]}{1 + exp[0,3(T − T2 )]}
A primeira equação diretamente descreve a resposta de Γ. Para gm
e Am,max, a equação é modificada usando as funções de inibição

19. Modelo A-gs

Taxa de Fotossíntese:
*

 − g m (Ci − Γ)  


Am = Am , max 1 − exp 

Am , max






 − ε Ia 
An = ( Am + Rd ) 1 − exp 
  − Rd
 Am + Rd  

Sendo que a eficiência da conversão da luz, respiração da folha
concentração interna de carbono e déficit de saturação são
respectivamente:
Cs − Γ
ε = ε0
C s + 2Γ
Am
Rd =
9

20. Modelo A-gs
Ci − Γ
*  1 − Ds
f ≡
= f0  *
 D
Cs − Γ
 max







Ds = qsat (Ts ) − qa
Este trabalho não leva em conta o stress hídrico do solo, devido ao
fato de que biologicamente a queda dos níveis de umidade na zona
de raízes afeta de maneira diferente a condutância estomatal nas
plantas. Cada espécie possui uma defesa específica ao stress
hídrico, como no caso das duas vegetações lenhosas estudadas por
Calvet et al, 2004, onde o pinheiro bravo tolera o secamento e o
carvalho alvarinho evita o secamento.
O stress hídrico do solo irá afetar a condutância do mesófilo e o
fator de conexão das plantas, porém de maneira singular para cada
espécie.
Modelagens genéricas para o stress hídrico do solo variam a
condutância do mesófilo multiplicando por um parâmetro de
umidade do solo.

21. Resultados Obtidos



Foram desenvolvidos dois modelos neste trabalho para o cálculo
da assimilação de CO2 (An), o primeiro chamado de ISBA baseado
em Noilhan and Planton (1989); Noilhan and Mahfouf (1996) e o
segundo de ISBA-A-gs baseado em Calvet et al., (1998); Calvet,
(2000).
Foi empregado o método numérico Runge Kutta de quarta ordem
para o cálculo das equações diferenciais (rotina extraída do livro
Numerical Recipes).
As séries de dados A e B forçaram os dois modelos e para
compará-los optou-se por selecionar os dados de saída entre os
dias 1 e 15 de dezembro de 2001 e 2002. Foi escolhido a primeira
quinzena do mês de dezembro pelo fato de que em 2001 foi seco e
em 2002 chuvoso neste período, tendo assim uma maior amplitude
dos fatores ambientais a serem estudados.

22. Resultados Obtidos

Condutância Estomatal e Assimilação de CO2:
No ano de 2001 a umidade do solo na zona de raízes chegou
próxima a umidade do ponto de murchamento, quando isso
ocorreu o ISBA-A-gs continuou a gerar An e gs potenciais com
relação ao stress hídrico do solo, pois o modelo não contempla o
secamento do solo, dessa forma o An e gs produzidos foram
maiores que do ISBA. Já em 2002 a umidade da zona de raízes
estava quase na saturação, nesse caso o ISBA superestimou A n e gs
gerando valores acima da taxa potencial do ISBA-A-gs.
No ISBA-A-gs a condutância do estômato e a assimilação de
CO2 diminuem ao meio dia como prevenção a perda excessiva de
água devido à fotoinibição da enzima rubisco.
O ISBA modela a condutância do estômato fisicamente, ele
não contempla a respiração celular realizada no período noturno,
processo este que pode ser visualizado na modelagem ISBA-A-gs.

23. Resultados Obtidos

24. Resultados Obtidos

25. Conclusões



No caso de uma vegetação que fora alagada por represamento,
pode-se utilizar parâmetros para a vegetação e solo que ali
existiam e dados meteorológicos medidos no período em questão
para forçar os modelos e gerar dados que agora não se podem mais
obter através de medições.
Ambos os modelos ISBA e ISBA-A-gs requerem parâmetros da
vegetação veg e LAI. No caso da cultura de soja esses parâmetros
variam ao longo do cultivo. Para melhor modelagem da interação
superfície-vegetação-atmosfera é necessário a inserção de mais
uma equação diferencial nos modelos acima para computar o
desenvolvimento da vegetação ao longo do tempo, tornando assim
o modelo dinâmico.
Para melhor modelagem do ISBA-A-gs deste trabalho é necessário
estudar a resposta biológica ao stress hídrico do solo, bem como
definir um valor para a condutância cuticular média da soja.