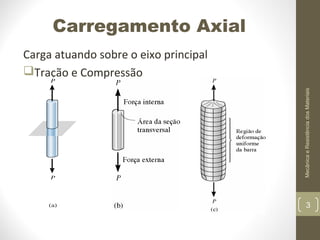
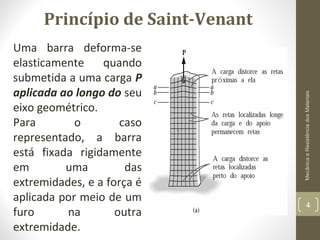
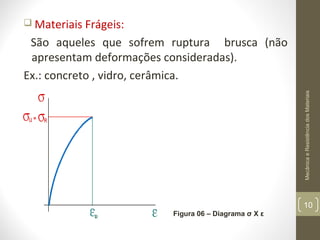
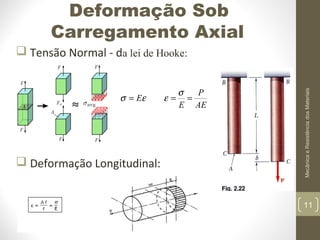
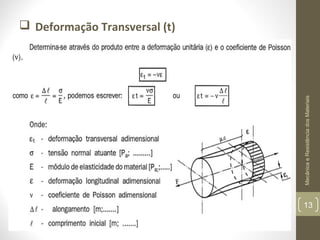
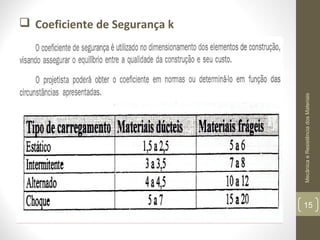
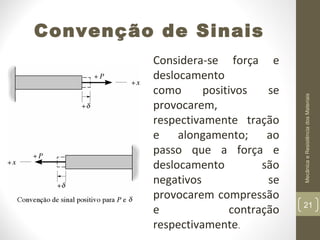
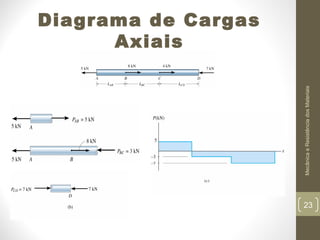
Este documento apresenta os principais conceitos de mecânica e resistência dos materiais, incluindo exemplos de estruturas sob carregamento axial, propriedades de materiais como elasticidade e plasticidade, e conceitos como tensão, deformação, módulo de Young, e concentração de tensões. O documento também discute cálculos para determinar a deformação de elementos sob carga axial usando a lei de Hooke.

1. Mecânica e Resistência dos Materiais
Eng.ª de Alimentos – 4º semestre
Docente: Jesumar
Discente: Érika C. A. S. Kurpel Daron
Taina Frances
Bruna F. C. M. Rostirola
Greice Nascimento
Amanda Rodrigues

2. Mecânica e Resistência dos Materiais
Exemplos de Estrutura
2

3. Carregamento Axial
Mecânica e Resistência dos Materiais
Carga atuando sobre o eixo principal
Tração e Compressão
3

4. Uma barra deforma-se
elasticamente
quando
submetida a uma carga P
aplicada ao longo do seu
eixo geométrico.
Para
o
caso
representado, a barra
está fixada rigidamente
em
uma
das
extremidades, e a força é
aplicada por meio de um
furo
na
outra
extremidade.
Mecânica e Resistência dos Materiais
Princípio de Saint-Venant
4

5. 1.1 Elasticidade
 Quando um corpo-de-prova do material é
descarregado, isto é, a carga é gradualmente diminuída
até zero, a deformação sofrida durante o
carregamento
desaparecerá
parcial
ou
completamente.
1.2 Tensão Admissível
 Para permitir sobrecargas acidentais, bem como
para levar em conta certas imprecisões na construção e
possíveis desconhecimentos de algumas variáveis na
análise as estrutura, normalmente emprega-se um
coeficiente de segurança, escolhendo-se uma tensão
admissível, ou tensão de projeto, abaixo do limite de
proporcionalidade.
Mecânica e Resistência dos Materiais
Propriedades
5

6. Mecânica e Resistência dos Materiais
1.3 Elasticidade Linear e Lei de Hooke
 Os diagramas tensão x deformação da maioria
dos materiais estruturais apresentam uma região
inicial de comportamento elástico linear. Quando
um material se comporta elasticamente e
apresenta, também, uma relação linear entre
tensão e deformação, diz-se que é linearmente
elástico.
σ = E. ε
6

7. Lei de Hooke
a relação de proporcionalidade entre tensão e
a deformação.
 O coeficiente de proporcionalidade ( E) entre a
tensão (σ) e a deformação (ε) é chamado de
MÓDULO DE ELASTICIDADE ou MÓDULO DE
YOUNG).
Figura 07 – Lei de
Hooke
Mecânica e Resistência dos Materiais
É
7

8. Mecânica e Resistência dos Materiais
Material Elástico Linear: obedece a Lei de
Hooke;
 Material não Elástico: não obedece a Lei de
Hooke;
 Material Plástico: material não elástico com
deformação residual;
 Material
Elastoplástico: material com
comportamento elástico, e após certo valor de
tensão, apresenta deformações residuais.
8

9.  Materiais Dúcteis: sofrem grandes deformações
antes de atingir a ruptura (com ou sem limite de
escoamento).
 Ex.: alumínio, aço.
Figura 05 – Diagrama σ X ε
Mecânica e Resistência dos Materiais
De maneira geral, existem os materiais Dúcteis e
Frágeis:
9

10.  Materiais Frágeis:
Mecânica e Resistência dos Materiais
São aqueles que sofrem ruptura brusca (não
apresentam deformações consideradas).
Ex.: concreto , vidro, cerâmica.
10
Figura 06 – Diagrama σ X ε

11. Deformação Sob
Carregamento Axial
σ = Eε
 Deformação Longitudinal:
ε=
σ
P
=
E AE
Mecânica e Resistência dos Materiais
 Tensão Normal - da lei de Hooke:
11

12.  A deformação é expressa por:
PL
δ=
AE
PL
δ =∑ i i
i Ai Ei
Mecânica e Resistência dos
Materiais
 Para variações da área da secção, propriedades
e/ ou cargas aplicadas:
12

13. Mecânica e Resistência dos Materiais
 Deformação Transversal (t)
13

14. Mecânica e Resistência dos Materiais
 Estricção
14

15. Mecânica e Resistência dos Materiais
 Coeficiente de Segurança k
15

16. Mecânica e Resistência dos Materiais
Como determinar a resistência de um
material?
16
Figura 03- Equipamento
para ensaio de tração

17. Mecânica e Resistência dos Materiais
Corpo de prova, máquina de ensaio, estricção
O diagrama carga x deformação é referente a barra analisada,
não podendo ser usado para prever deformações de outras
barras com outras dimensões.
17

18. Mecânica e Resistência dos Materiais
 Caracteriza as propriedades do material e não
depende das dimensões da amostra.
 A relação (σ x ε) depende:
 Tipo de material;
 Intensidade do esforço aplicado.
 É também denominada relação constitutiva do
material.
 A relação é medida através de ensaios de tração
ou compressão.
18

19. A partir da aplicação da lei de Hooke e das
definições de tensão e deformação , pode-se
desenvolver uma equação para determinar a
deformação elástica de um elemento submetido a
cargas axiais.
σ = P(x) / A(x)
ε = dδ / dx
PL
δ =∑ i i
i Ai Ei
Mecânica e Resistência dos Materiais
Deformação Elástica de um
Elemento Submetido a Carga
Axial
19

20. Em muitos casos, a barra tem área da seção
transversal constante A; o material será
homogêneo, logo E é constante. Além disso, se uma
força externa constante for aplicada em cada
extremidade como mostra a figura, então a força
interna P ao longo de todo o comprimento da barra
também será constante.
PL
δ=
AE
Mecânica e Resistência dos Materiais
Carga Uniforme e Seção
Transversal Constante
20

21. Considera-se força e
deslocamento
como
positivos
se
provocarem,
respectivamente tração
e alongamento; ao
passo que a força e
deslocamento
são
negativos
se
provocarem compressão
e
contração
respectivamente.
Mecânica e Resistência dos Materiais
Convenção de Sinais
21

22. Se a barra for submetida a diversas forças axiais
diferentes ou, ainda, a área da seção transversal
ou o módulo de elasticidade mudarem
abruptamente de uma região para outra da
barra, deve-se calcular o deslocamento para
cada segmento da barra e então realizar a
adição algébrica dos deslocamentos de cada
segmento.
Pi Li
δ =∑
i Ai Ei
Mecânica e Resistência dos Materiais
Barra com Diversas
Forças Axiais
22

23. Mecânica e Resistência dos Materiais
Diagrama de Cargas
Axiais
23

24. Tensão térmica
δt = α ∆T L
α = coeficiente linear de expansão térmica,
propriedade do material
∆T = variação na temperatura do elemento
L = comprimento inicial do elemento
δt= variação no comprimento do elemento
Mecânica e Resistência dos Materiais
Uma mudança na temperatura pode provocar
alterações nas dimensões de um material.
24

25.  Concentrações de tensão ocorrem em seções
onde a área da seção transversal muda
repentinamente. K = σ máx. / σ méd.
 Tensão máxima é determinada usando uma fator
de concentração de tensão, K, o qual é uma função
de geometria.
Mecânica e Resistência dos Materiais
Concentrações de
Tensão
25

26. Referências
 http://www.google.com.br/651 - (Acessado em 3 de março de 2013).
 http://www.caetano.eng.br/aulas/2012b/rm2.php: acessado em 01
de março de 2013.
 http://www.google.com.br/#hl=pt-BR&output=search&sclient=psyab&q=ppt+carregamento+axial&oq=ppt+carregamento+axial&gs_l=h
p.3...11397.18266.0.19266.22.22.0.0.0.0.519.6992.23j10j5j1.19.0...0.0...1c.1.5.psyab.F0a3FgfQASg&pbx=1&bav=on.2,or.r_qf.&bvm=bv.43287494,d.eW
U&fp=99cea6fe1bcfc673&biw=1366&bih=651: acessado em 03 de
março de 2013.
 http://www.google.com.br/#hl=pt-BR&output=search&sclient=psyab&q=ppt+carregamento+axial&oq=ppt+carregamento+axial&gs_l=h
p.3...11397.18266.0.19266.22.22.0.0.0.0.519.6992.23j10j5j1.19.0...0.0...1c.1.5.psyab.F0a3FgfQASg&pbx=1&bav=on.2,or.r_qf.&bvm=bv.43287494,d.eW
U&fp=99cea6fe1bcfc673&biw=1366&bih=651: acessado em
06/03/2013.
Mecânica e Resistência dos Materiais
Disponível em:
26

27. Mecânica e Resistência dos Materiais
Perguntas
27

28. Mecânica e Resistência dos Materiais
OBRIGADO !!!!!
28