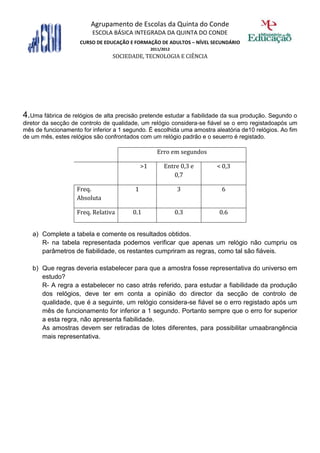
1) O documento discute conceitos de probabilidade e estatística, apresentando vários exercícios e problemas para cálculo de probabilidades. 2) Inclui uma tabela listando todos os resultados possíveis do lançamento de dois dados e pede para calcular várias probabilidades associadas. 3) Também apresenta dados sobre um estudo da fiabilidade de relógios e pede para analisar os resultados obtidos e estabelecer regras para uma amostra representativa.

1. Agrupamento de Escolas da Quinta do Conde
ESCOLA BÁSICA INTEGRADA DA QUINTA DO CONDE
CURSO DE EDUCAÇÃO E FORMAÇÃO DE ADULTOS – NÍVEL SECUNDÁRIO
2011/2012
SOCIEDADE, TECNOLOGIA E CIÊNCIA
Área de Competência – Sociedade, Tecnologia e Ciência (STC)
Núcleo gerador 1: Equipamentos – Princípios de funcionamento
Temas: Aspectos do raciocínio matemático fundamentais para a utilização e gestão de equipamentos e sistemas
técnicos
Recursos/materiais: Computador, Recursos Multimédia, BE/CRE, Internet.
Formadores: César Barros/João Novais Formando :Luís António Parreira Moura
Ficha de Trabalho n.º 3
1.Num caderno de Matemática há 40 exercícios (15 de Probabilidades, 13 de Equações e 12
de trigonometria), numerados aleatoriamente de 1 a 40 e sem conhecimento dos alunos. O
professor propõe aos alunos que escolham, ao acaso, o número correspondente ao exercício
que querem resolver.
1.1)Det
ermine a probabilidade de o 1º exercício ser de Probabilidades.
1.2) Determine a probabilidade de o 1º exercício ser de Probabilidades ou de Trigonometria.
1.3) Se o 1º exercício foi de Equações, qual é a probabilidade de o próximo também ser de
Equações?
2.Um saco contém 6 bolas do mesmo tamanho, feitas do mesmo material e numeradas de 1 a
6. Com os olhos fechados, tiram-se simultaneamente 2 bolas.
2.1) Quais são os casos possíveis?R- os casos possíveis são 151,1; 1,3; 1,4; 1,5; 1,6; 2,3;2,4;
2,5; 2,6; 3,4; 3,5; 3,6; 4,5; 4,6; 5,6
2.2) Qual é a probabilidade de tirar dois números pares? A probalidade de tirar 2 números
pares é de 20%

2. Agrupamento de Escolas da Quinta do Conde
ESCOLA BÁSICA INTEGRADA DA QUINTA DO CONDE
CURSO DE EDUCAÇÃO E FORMAÇÃO DE ADULTOS – NÍVEL SECUNDÁRIO
2011/2012
SOCIEDADE, TECNOLOGIA E CIÊNCIA
2.3)Qual é a probabilidade de tirar dois números ímpares?Aprobalidade é de 20%
3.Na seguinte tabela estão apresentados todos os acontecimentos elementares do lançamento
de dois dados, tendo-se observado o número das faces voltadas para cima.
3.1) Indique o número de todos os acontecimentos possíveis.
Há 36 casos possíveis.
3.2) Classifique os seguintes acontecimentos:
I. A soma das faces é inferior a 2.
A probalidade é nula o acontecimento é impossível.
II. A soma das faces é inferior a 13.
A probalidade é de 100%, acontecimento certo.
III. O produto das faces é múltiplo de 3.
O número casos favoráveis é de 14.O 1 2 3 4 5 6
acontecimento é possível. 1 (1 , 1) (1 , 2) (1 , 3) (1 , 4) (1 , 5) (1 , 6)
2 (2 , 1) (2 , 2) (2 , 3) (2 , 4) (2 , 5) (2 , 6)
3 (3 , 1) (3 , 2) (3 , 3) (3 , 4) (3 , 5) (3 , 6)
3.3)Determina a probabilidade de saírem: 4 (4 , 1) (4 , 2) (4 , 3) (4 , 4) (4 , 5) (4 , 6)
5 (5 , 1) (5 , 2) (5 , 3) (5 , 4) (5 , 5) (5 , 6)
3.3.1) Dois números iguais. 6 (6 , 1) (6 , 2) (6 , 3) (6 , 4) (6 , 5) (6 , 6)
3.3.2) Dois números ímpares.
3.3.3) Dois números pares.
3.3.4) Dois números em que um seja múltiplo do outro.
3.3.5) Dois números primos.

3. Agrupamento de Escolas da Quinta do Conde
ESCOLA BÁSICA INTEGRADA DA QUINTA DO CONDE
CURSO DE EDUCAÇÃO E FORMAÇÃO DE ADULTOS – NÍVEL SECUNDÁRIO
2011/2012
SOCIEDADE, TECNOLOGIA E CIÊNCIA
4.Uma fábrica de relógios de alta precisão pretende estudar a fiabilidade da sua produção. Segundo o
diretor da secção de controlo de qualidade, um relógio considera-se fiável se o erro registadoapós um
mês de funcionamento for inferior a 1 segundo. É escolhida uma amostra aleatória de10 relógios. Ao fim
de um mês, estes relógios são confrontados com um relógio padrão e o seuerro é registado.
Erro em segundos
>1 Entre 0,3 e < 0,3
0,7
Freq. 1 3 6
Absoluta
Freq. Relativa 0.1 0.3 0.6
a) Complete a tabela e comente os resultados obtidos.
R- na tabela representada podemos verificar que apenas um relógio não cumpriu os
parâmetros de fiabilidade, os restantes cumpriram as regras, como tal são fiáveis.
b) Que regras deveria estabelecer para que a amostra fosse representativa do universo em
estudo?
R- A regra a estabelecer no caso atrás referido, para estudar a fiabilidade da produção
dos relógios, deve ter em conta a opinião do director da secção de controlo de
qualidade, que é a seguinte, um relógio considera-se fiável se o erro registado após um
mês de funcionamento for inferior a 1 segundo. Portanto sempre que o erro for superior
a esta regra, não apresenta fiabilidade.
As amostras devem ser retiradas de lotes diferentes, para possibilitar umaabrangência
mais representativa.