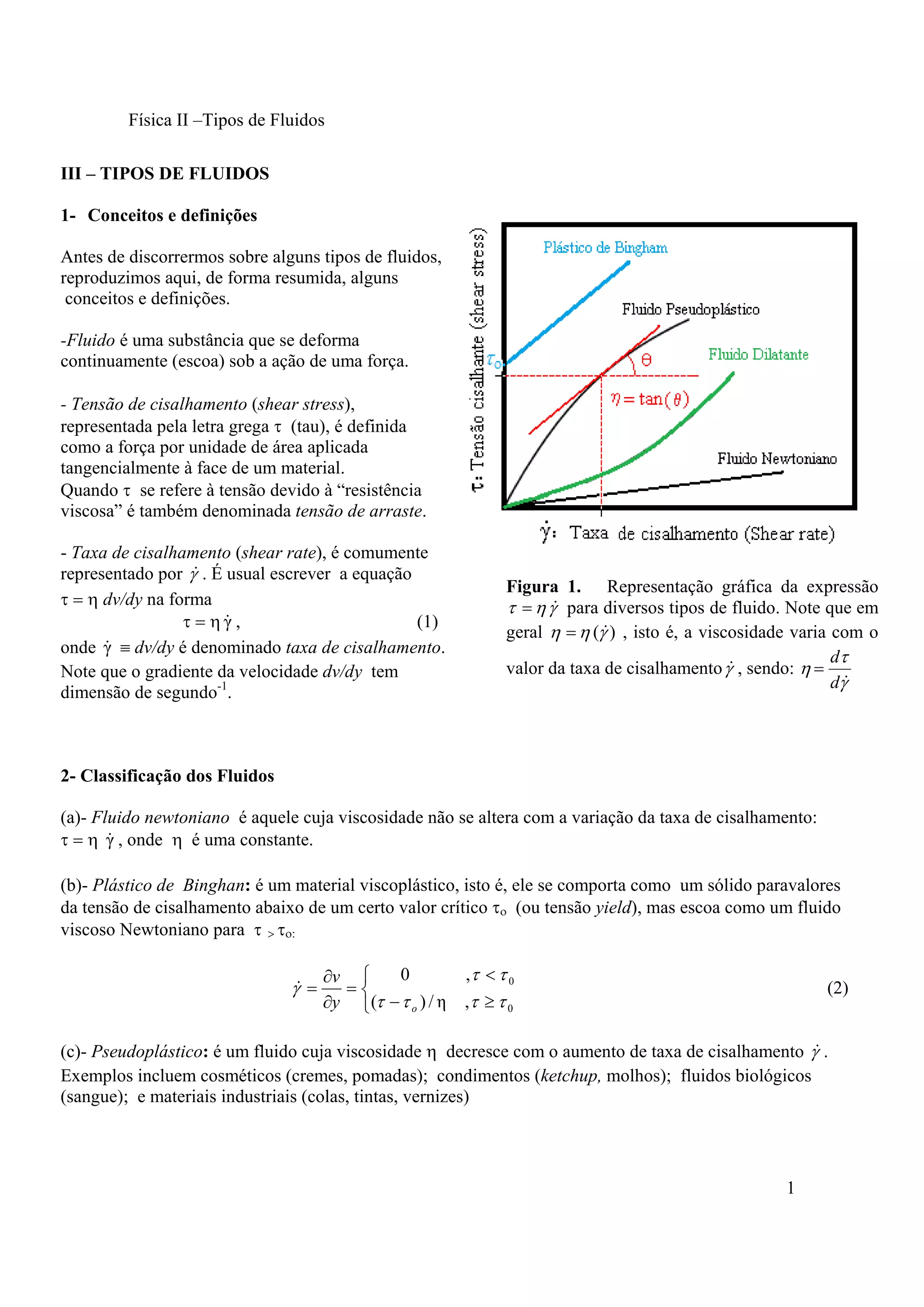
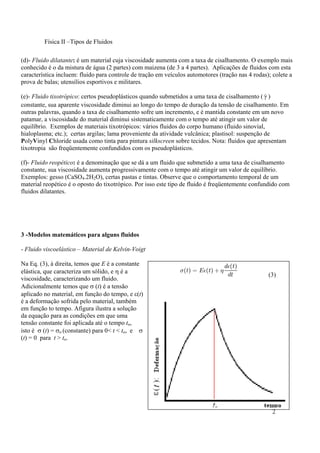
O documento descreve diferentes tipos de fluidos, incluindo fluidos newtonianos, cuja viscosidade é constante; fluidos plásticos e pseudoplásticos, cuja viscosidade varia com a taxa de cisalhamento; e fluidos dilatantes, tixotrópicos e reopéticos, cuja viscosidade varia com o tempo sob tensão de cisalhamento constante. Modelos matemáticos como fluidos de Lei de Potência, cruzantes e de Carreau são discutidos.

1. Física II –Tipos de Fluidos
1
III – TIPOS DE FLUIDOS
1- Conceitos e definições
Antes de discorrermos sobre alguns tipos de fluidos,
reproduzimos aqui, de forma resumida, alguns
conceitos e definições.
-Fluido é uma substância que se deforma
continuamente (escoa) sob a ação de uma força.
- Tensão de cisalhamento (shear stress,
representada pela letra grega tau), é definida
como a força por unidade de área aplicada
tangencialmente à face de um material.
Quando  se refere à tensão devido à “resistência
viscosa” é também denominada tensão de arraste.
- Taxa de cisalhamento (shear rate), é comumente
representado por  . É usual escrever a equação
 dv/dy na forma
   γ , (1)
onde γ  dv/dy é denominado taxa de cisalhamento.
Note que o gradiente da velocidade dv/dy tem
dimensão de segundo-1
.
2- Classificação dos Fluidos
(a)- Fluido newtoniano é aquele cuja viscosidade não se altera com a variação da taxa de cisalhamento:
 γ , onde  é uma constante.
(b)- Plástico de Binghan: é um material viscoplástico, isto é, ele se comporta como um sólido paravalores
da tensão de cisalhamento abaixo de um certo valor crítico  (ou tensão yield), mas escoa como um fluido
viscoso Newtoniano para 









0
0
,η/)(
,0



oy
v
 (2)
(c)- Pseudoplástico: é um fluido cuja viscosidade  decresce com o aumento de taxa de cisalhamento  .
Exemplos incluem cosméticos (cremes, pomadas); condimentos (ketchup, molhos); fluidos biológicos
(sangue); e materiais industriais (colas, tintas, vernizes)
Figura 1. Representação gráfica da expressão
  para diversos tipos de fluido. Note que em
geral )(  , isto é, a viscosidade varia com o
valor da taxa de cisalhamento , sendo:



d
d


2. Física II –Tipos de Fluidos
2
(d)- Fluido dilatante: é um material cuja viscosidade aumenta com a taxa de cisalhamento. O exemplo mais
conhecido é o da mistura de água (2 partes) com maizena (de 3 a 4 partes). Aplicações de fluidos com esta
característica incluem: fluido para controle de tração em veículos automotores (tração nas 4 rodas); colete a
prova de balas; utensílios esportivos e militares.
(e)- Fluido tixotrópico: certos pseudoplásticos quando submetidos a uma taxa de cisalhamento ( γ )
constante, sua aparente viscosidade diminui ao longo do tempo de duração da tensão de cisalhamento. Em
outras palavras, quando a taxa de cisalhamento sofre um incremento, e é mantida constante em um novo
patamar, a viscosidade do material diminui sistematicamente com o tempo até atingir um valor de
equilíbrio. Exemplos de materiais tixotrópicos: vários fluidos do corpo humano (fluido sinovial,
hialoplasma; etc.); certas argilas; lama proveniente da atividade vulcânica; plastisol: suspenção de
PolyVinyl Chloride usada como tinta para pintura silkscreen sobre tecidos. Nota: fluidos que apresentam
tixotropia são freqüentemente confundidos com os pseudoplásticos.
(f)- Fluido reopético: é a denominação que se dá a um fluido que submetido a uma taxa de cisalhamento
constante, sua viscosidade aumenta progressivamente com o tempo até atingir um valor de equilíbrio.
Exemplos: gesso (CaSO4.2H2O), certas pastas e tintas. Observe que o comportamento temporal de um
material reopético é o oposto do tixotrópico. Por isso este tipo de fluido é freqüentemente confundido com
fluidos dilatantes.
3 -Modelos matemáticos para alguns fluidos
- Fluido viscoelástico – Material de Kelvin-Voigt
Na Eq. (3), à direita, temos que E é a constante
elástica, que caracteriza um sólido, e é a
viscosidade, caracterizando um fluido.
Adicionalmente temos que  (t) é a tensão
aplicado no material, em função do tempo, e (t)
é a deformação sofrida pelo material, também
em função to tempo. Afigura ilustra a solução
da equação para as condições em que uma
tensão constante foi aplicada até o tempo to,
isto é  (t) = o (constante) para 0< t < to, e 
(t) = 0 para t > to.
(3)

3. Física II –Tipos de Fluidos
3
- Fluido de Newton generalizado.
Trata-se de um fluido para o qual a tensão de cisalhamento  é uma função da taxa de cisalhamento 
(gradiente de velocidade). Em termos matemáticos
)γ(F (4)
onde F = F( γ ) é uma função genérica de γ (taxa de cisalhamento); γ  ∂v/∂y (gradiente de velocidade
perpendicular ao plano de cisalhamento). A quantidade
γ/)γ(ηef
F (5)
é denominada viscosidade efetiva, ou viscosidade aparente. Exemplos:
* Fluido Lei de Potência obedece a relação
n
γK
onde K é uma constante, n é um inteiro (1, 2, 3 , ...), e γ é a taxa de
cisalhamento. A viscosidade efetiva efη , como uma função de γ , é então
1-n
ef γ)γ(η  K
* Fluido cruzante é definidos por sua viscosidade efetiva efη , como
n







 1
*
0
0
ef
γη
1
η
)γ(η



onde 0η e *
 são constantes, e n = 1, 2, 3, ... (inteiro). Note que: Para n = 1, o
comportamento é de fluido newtoniano. Mas para n > 1 temos duas condições a
considerar: para *
0 γη  (a razão 1/γη *
0  ) e o fluido se comporta como
fluido “lei de potência“ , enquanto que no limite *
0 γη  seu comportamento
é o de um fluido newtoniano.
* Fluido de (Pierre) Carreau obedece a relação
  2
1
2
0ef )γ(1η)γ(η


n
 

4. Física II –Tipos de Fluidos
4
onde nand,η0  são constantes. Este fluido se comporta como fluido
newtoniano se 1γ  , e como fluido lei de potência se 1γ 