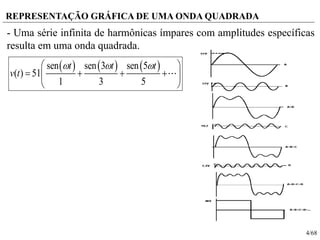
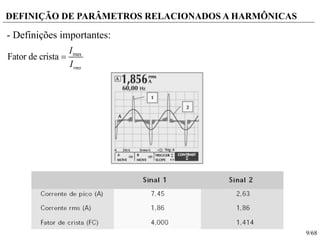
O documento descreve conceitos relacionados a conversores CC-CA e inversores monofásicos e trifásicos. Discutem-se representações de ondas senoidais por séries de Fourier, definição de potência ativa e reativa em condições senoidais e não senoidais, e parâmetros relacionados a harmônicas. Também são apresentados circuitos e análises de inversores monofásicos em meia ponte e ponte completa alimentando cargas resistivas e RL. Por fim, faz-se menção a inversores trifás




























![31/68
CONVERSORES CC-CA INVERSOR TRIFÁSICO COM CONDUÇÃO
POR 120 E CARGA R
Modo 1 [0, /3]:
Modo 2 [/3, 2/3]:
Modo 3 [2/3, ]:](https://image.slidesharecdn.com/03conversorescc-cainversores-170310133311/85/03-conversores-cc-ca-inversores-31-320.jpg)




































