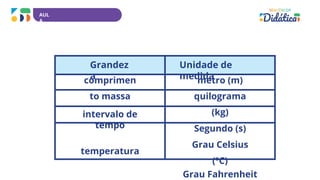
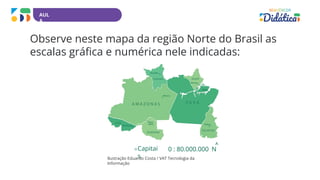
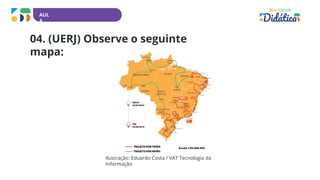
Este documento apresenta uma sequência didática de matemática para o 9o ano do ensino fundamental. A sequência aborda os temas de grandezas, proporcionalidade direta e inversa, e conversão de unidades de medida. A sequência é composta por 5 aulas que utilizam atividades práticas e investigativas para desenvolver habilidades relacionadas a esses conceitos.