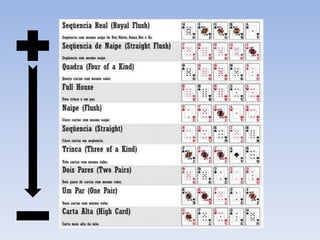
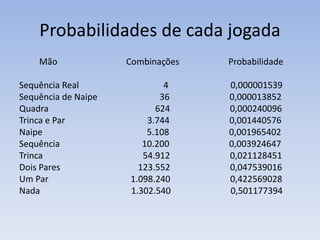
O documento descreve as regras e conceitos básicos do jogo de pôquer. Em três frases: O pôquer é jogado com baralho completo de 52 cartas, cada jogador recebe duas cartas e cinco são colocadas na mesa. O jogo consiste em quatro rodadas de apostas à medida que novas cartas são reveladas na mesa. O objetivo é formar a combinação de cartas mais rara para ganhar o pot de apostas.

1. Pôquer
Prof.Dr. Nilo Sampaio
Angelo Fortunato
Bruno Figueiredo Teixeira
Carlos Chaves Fernandes
Carlos Eduardo Toledo da Silva Ramos
Cauê Lemes da Silva
Guilherme Rozante Haddad
Kaique Gomes Corrêa
Robert dos Santos Matoso Lobos

2. Como Jogar
Joga-se com UM baralho de 52 cartas (completo)
Cada jogador recebe DUAS cartas e são colocadas
CINCO sobre a mesa
O jogo consiste em QUATRO rodadas de apostas

3. 1ª Rodada
Acontece após todos os jogadores receberem
suas cartas
Para continuar no jogo é necessário fazer uma
aposta mínima

4. 2ª Rodada
Acontece após o FLOP
É uma rodada importante pois o jogador
conhece TRÊS cartas da mesa

5. 3ª Rodada
Acontece após o primeiro TURN
Pode-se fazer mais apostas

6. Vencedor
O jogador que possuir a combinação de cartas
mais rara ganha o POT de apostas

8. Probabilidades de cada jogada
Mão Combinações Probabilidade
Sequência Real 4 0,000001539
Sequência de Naipe 36 0,000013852
Quadra 624 0,000240096
Trinca e Par 3.744 0,001440576
Naipe 5.108 0,001965402
Sequência 10.200 0,003924647
Trinca 54.912 0,021128451
Dois Pares 123.552 0,047539016
Um Par 1.098.240 0,422569028
Nada 1.302.540 0,501177394

9. Estudo de caso
• Caso 1
• Caso 2

10. Caso 1

14. Caso 2

19. Regras do Jogo:
• Pode ser jogado com apenas um ou até oito
baralhos;
• O limite mínimo das aposta geralmente é de
US$5,00 e o máximo
variam de US$100 até
US$50.000,00;

20. • As mesas acomodam geralmente seis
jogadores, incluindo o crupiê (que tem a
função de embaralhar e dar as cartas);

21. • As cartas de 2 à 10 têm seu valor igual ao
número ;
• Os valetes, damas e reis têm seu valor
equivalente à 10 pontos;
• Já o ás pode valer 1 ou 11 pontos, sendo
determinado o valor para uma mão mais
vantajosa;
• Os naipes não influenciam no valor das cartas,
ou seja, um quatro de paus terá o mesmo
valor de quatro de copas;

22. • O jogo inicia quando os jogadores, começando pelo
lado esquerdo do crupiê, colocam suas apostas;
• Não tendo mais
apostas a fazer,
são distribuídas duas
cartas para cada
jogador viradas para
cima, já as do cupriê,
uma é virada para
baixo e a outra para
cima;

23. • O objetivo do Blackjack é conseguir somar 21 pontos
com as cartas ou chegar no valor mais próximo, sem
ultrapassa-lo;
• A melhor mão possível é fazer os 21 pontos com as
duas primeiras cartas, que é o Blackjack. Com isso o
jogador ganha 3:2, ou seja, se o jogador apostar
US$5,00, ele irá receber US$7,50 a mais do que foi
apostado;

24. • Os jogadores que derrotarem a mão do crupiê
receberão o dobro de suas apostas, para isso
deverão ter somado mais pontos que não
extrapole(passe de 21 pontos) ;
• Caso o jogador e o crupiê somem 21, o
jogador receberá de volta sua aposta;
• Se o jogador tiver uma mão com poucos
pontos, ele pode pedir quantas cartas quiser,
tendo cuidado apenas para não extrapolar;

25. Termos usados no Blackjack:
• Pedir carta (Hint):
Após receber as duas primeiras cartas, o jogador
pode pedir mais quantas cartas quiser, desde que
não extrapole (some mais do que 21);
• Render-se (surrender):
Em alguns cassinos, caso os jogadores vejam que
o crupiê tem muita chance de ganhar, é possível
que desistam de suas cartas e percam apenas
metade de sua aposta original;

26. • Dobrar (Double Down)
Isso ocorre quando um jogador sente que só
precisa de uma única carta adicional, dobrando
sua aposta e podendo receber uma carta;
• Extrapolar ou quebrar (bust/break)
Se as cartas de um jogador excederem 21, diz-se
que "extrapolaram". Com isso, ele perde sua
aposta;

27. • Dividir (split)
Apenas pode ser feita quando o jogador recebe
duas cartas idênticas na primeira rodada, com
isso o jogo é dividido em duas mãos com a
mesma aposta que foi
feita antes;

28. Legenda
Tabela que auxilia jogadores
inexperientes na hora de pedir carta,
parar, dobrar ou dividir:

30. Estudo de caso
• Caso 1
• Caso 2
• Caso 3
• Caso 4

31. Caso 1:
Qual a probabilidade de ganhar com essas cartas?
Se mão do crupiê for essa

32. Resposta
Para ganhar sem fazer split ele precisa que a
carta do crupiê seja de valor menor que 10.
No baralho sobraram 36 cartas com valor que
buscamos, isso de 49 cartas que sobraram.
Significa que de 49 possibilidades, 36 deles nos
satisfazem , isso da 49 – 100%
36 – R
R = 73,47 % essa e a probabilidade de o
jogador ganhar com essas mãos em jogo.

33. Caso 2:
Qual a probabilidade de fazer um Blackjack?

34. Resposta
Para isso o jogador vai ter que ganhar uma carta
valendo 10 e um Ás.
Existem 4 áses entre 52 cartas. O que nos da a
probabilidade de 4/52 = 7,7%
A probabilidade de tirar uma carta valendo 10 e
de 16/52 = 30,8%
Então a probabilidade de tirar as 2 ao mesmo
tempo e de 30,8% x 7,7% = 2,41% de chance.

35. Caso 3:
Qual a probabilidade de pedir uma carta e não
passar de 21 pontos?
• Cartas do Jogador
• Cartas do Crupiê

36. Resposta
Para isso o jogador vai ter que pegar uma carta de
valor entre 1 e 7. Qualquer uma com valor maior
passa do limite. Já sabemos que uma das cartas do
crupiê é um sete, então temos nas possibilidades
que satisfazem a situação: 4 ases, 4 dois, 4 três, 3
quatros, 4 cincos, 4 seis e 3 setes. O número de
total de possibilidades é de 49, então temos a
chance de 26 que satisfazem entre 49
possibilidades. Então a probabilidade de pegarmos
uma carta com valor ate 7 e de 26/49 = 0,5306.
Que equivale 53,06%.

37. Caso 4:
Qual a probabilidade de empate entre o crupiê e
o jogador ambos com blackjack?

38. Resposta
Para isso primeiro temos que pensar nas cartas
que o jogador precisa que são um ás e uma
carta de valor 10. Vamos usar a formula da
probabilidade binomial na qual calcularemos o
resultado.
P = 𝐶 𝑛 . r . 𝑝 𝑟
. 𝑞 𝑛−𝑟
10.P=C2,2*(0,024)^2*(0,976)^0→P≅0,000576

40. História
• O jogo aparentemente surgiu na China e sua criação é atribuída a
um santo soldado chinês chamado Hung Ming, que viveu de
243 a.C a 182 a.C. O conjunto tradicional de dominós, conhecido
como sino-europeu, é formado por 28 peças, ou pedras. Cada face
retangular de dominó é divida em duas partes quadradas, ou
"pontas", que são marcadas por um número de pontos de 0 a 6, ou
deixadas em branco.

41. Pedras
• As pedras são geralmente denominadas de acordo com os
números em suas pontas. Assim, uma pedra com um 3 de um lado
e um 4 do outro, é chamada de três-quatro, por exemplo. Peças
com números iguais em ambas as pontas são chamadas "duplos".
Em um jogo de peças, as peças são únicas.
• Pedras com o mesmo número em uma das pontas são
consideradas do mesmo naipe. Por exemplo 1-0, 1-1, 1-2, 1-3, 1-4,
1-5 e 1-6 pertencem todas ao naipe de "1", sendo que cada peça,
exceto os duplos, sempre irão pertencer a dois naipes.
• Na forma clássica do jogo, são sete números (de zero a seis),
combinados entre si. Matematicamente: C(7,2) + 7 = C(8,2) = 28.

42. Regras
• No Brasil, a forma mais comum de jogar, é por quatro
jogadores individuais, que receberão sete pedras cada
um , pode-se também jogar entre duplas (4 jogadores
2x2), onde cada jogador recebe 6 ou 7 peças, ou jogar-se
em 2 ou 3 jogadores com 6 ou 7 pedras cada um e o
restante das pedras ficam para comprar no caso do
oponente não ter a pedra da vez, o oponente deve
comprar até que encontre a peça que possa usar, não se
pode em nenhuma hipótese comprar peças a mais, ou
seja continuar comprando pedras mesmo depois de ter
pegado a pedra que da vez (a que você passou), para
não prejudicar os demais, se isso for realizado é
considerado roubo e a partida é recomeçada, ao jogador
que realizar esse "roubo" lhe será retirado 2 pontos.

43. Regras
• O Jogo 4x4
As peças são "embaralhadas" na mesa, e cada jogador pega 7 peças para
jogar. O jogador que começa a partida é o que tem a maior dupla. Ele
inicia a partida colocando esta peça no centro da mesa. A partir daí, joga-
se no sentido anti-horário. Cada jogador deve tentar encaixar alguma
peça sua nas peças que estão na extremidade do jogo, uma por vez.
Quando um jogador consegue encaixar uma peça, a vez é passada para o
próximo jogador. Caso o jogador não tenha nenhuma peça que encaixe
em qualquer lado, ele deve passar a vez, sem jogar peça nenhuma. A
partida pode terminar em duas circunstâncias: quando um jogador
consegue bater o jogo, ou quando o jogo fica trancado. Neste Caso Vence
a partida quem possuir menos peças em mão.

44. Regras
• Contagem
Caso algum jogador tenha batido o jogo, sua dupla leva todos os
pontos das peças que estão nas mãos dos adversários. Caso o jogo
fique trancado, conta-se todos os pontos conseguidos por cada
dupla. A dupla que possuir menos pontos é a vencedora, e leva
todos os pontos da dupla adversária. Caso haja um empate nesta
contagem de pontos, a dupla que trancou o jogo perde, e a dupla
vencedora leva todos os pontos desta dupla. Os pontos da dupla
vencedora são acumulados, e o jogo termina quando uma das
duplas atinge a marca de 50 pontos.
• Valor em pontos
O valor em pontos de cada peça corresponde à soma dos valores
das duas pontas da peça. Dessa forma, a peça 0-0 vale 0 pontos, a
peça 3-4 vale 7 pontos, a peça 6-6 vale 12 pontos e assim por
diante.

45. Probabilidade
• Espaço Amostral :
C(8,2) = 28 peças
Formada por números de 0-6 , sendo que cada Número aparece 8
vezes.
Dupla Ponta Iguais : 1 peça de cada Número

46. Probabilidade
Partida Aleatória de Dominó:
• Probabilidade 1
Probabilidade do jogador 2 ter uma peça (6).
Jogador 1: 3 peças na mão (6).
1 peça no jogo (6).
Monte de Compra: 14 peças
Jogador 1: 6 peças
Jogador 2: 7 peças
P1= C7,1 x (3/21)^1 x (18/21)^6 = 39,66%

47. Probabilidade
• Probabilidade 2
Probabilidade do jogador 1 ter uma peça (6) ou (0).
Jogador 2: 2 peças na mão (6).
2 peças no jogo (6).
1 peça na mão (0).
1 peça no jogo (0).
Monte de Compra: 14 peças
Jogador 1: 6 peças
Jogador 2: 6 peças
P2=C6,1 x (3/20)^1 x (17/20)^5 + C6,1 x (5/20)^1 x (15/20)^5= 75,52%

48. Probabilidade
• Probabilidade 3
Probabilidade do jogador 2 ter uma peça (2) ou (0).
Jogador 1: 1 peça na mão (2).
1 peça no jogo (2).
1 peça na mão (0).
1 peça no jogo (0).
Monte de Compra: 14 peças
Jogador 1: 5 peças
Jogador 2: 6 peças
P3=C6,1 x (5/20)^1 x (15/20)^5 + C6,1 x (5/20)^1 x (15/20)^5= 71,19%

49. Probabilidade
• Probabilidade 4
Probabilidade do jogador 1 ter uma peça (2) ou (0).
Jogador 2: 1 peça na mão (2).
2 peças no jogo (2).
1 peça na mão (0).
1 peça no jogo (0).
Monte de Compra: 14 peças
Jogador 1: 5 peças
Jogador 2: 5 peças
P4= C5, 1 x (4/19)^1 x (15/19)^4 + C5,1 x (5/19)^1 x (14/19)^4=79,68%

50. Probabilidade
• Probabilidade 5
Probabilidade do jogador 2 ter uma peça (1) ou (0).
Jogador 1: 2 peças na mão (1).
2 peças no jogo (1).
1 peça na mão (0).
1 peça no jogo (0).
Monte de Compra: 14 peças
Jogador 1: 4 peças
Jogador 2: 5 peças
P5= C5, 1 x (4/19)^1 x (15/19)^4 + C5,1 x (5/19)^1 x (14/19)^4= 79,68%

51. Probabilidade
• Probabilidade 6
Probabilidade do jogador 1 ter uma peça (0).
Jogador 2: 0 peças na mão (0).
2 peças no jogo (0).
Monte de Compra: 14 peças
Jogador 1: 4 peças
Jogador 2: 4 peças
P6= C4,1 x (5/18)^1 x (13/18)^3 = 41,86%

52. Probabilidade
• Probabilidade 7
Probabilidade do jogador 2 ter uma peça (0) ou (3).
Jogador 1: 1 peça na mão (3).
1 peça no jogo (3).
0 peça na mão (0).
3 peças no jogo (0).
Monte de Compra: 14 peças
Jogador 1: 3 peças
Jogador 2: 4 peças
P7= C4,1 x (5/18)^1 x (13/18)^3 + C4,1 x (4/18)^1 x (14/18)^3= 83,68%

53. Probabilidade
• Probabilidade 8
Probabilidade do jogador 1 ter uma peça (0) ou (1).
Jogador 2: 0 peça na mão (0).
3 peças no jogo (0).
0 peças na mão (1).
3 peças no jogo (1).
Monte de Compra: 14 peças
Jogador 1: 3 peças
Jogador 2: 3 peças
P8= C3, 1 x (4/17)^1 x (13/17)^2 + C3,1 x (4/17)^1 x (13/17)^2= 82,56%

54. Probabilidade
• Probabilidade 9
Probabilidade do jogador 2 ter uma peça (0) ou (6).
Jogador 1: 0 peça na mão (0).
3 peças no jogo (0).
2 peças na mão (6).
4 peças no jogo (6).
Monte de Compra: 14 peças
Jogador 1: 2 peças
Jogador 2: 3 peças
P9= C3, 1 x (4/17)^1 x (13/17)^2 + C3,1 x (1/17)^1 x (16/17)^2= 56,91%

55. Probabilidade
• Probabilidade 10
Probabilidade do jogador 1 ter uma peça (0) ou (4).
Jogador 2: 0 peça na mão (0).
3 peças no jogo (0).
2 peças na mão (4).
1 peça no jogo (4).
Monte de Compra: 14 peças
Jogador 1: 2 peças
Jogador 2: 2 peças
P10= C2, 1 x (4/16)^1 x (12/16)^1 + C2,1 x (4/16)^1 x (12/16)^1= 75%

56. Probabilidade
• Probabilidade 11
Probabilidade do jogador 2 ter uma peça (4) ou (5).
Jogador 1: 0 peça na mão (4).
1 peça no jogo (4).
2 peças na mão (5)
1 peça no jogo (5).
Monte de Compra: 13 peças
Jogador 1: 2 peças
Jogador 2: 2 peças
P11= C2, 1 x (6/15)^1 x (10/15)^1 + C2,1 x (4/15)^1 x (11/15)^1= 92,44%

57. Probabilidade
• Probabilidade 12
Probabilidade do jogador 1 ter uma peça (4).
Jogador 2: 1 peça na mão (4).
2 peças no jogo (4)
2 peças no jogo (4)
Monte de Compra: 13 peças
Jogador 1: 2 peças
Jogador 2: 1 peça
P12= C2, 1 x (4/15)^1 x (11/15)^1=39,11%

58. Probabilidade
• Probabilidade 12
Probabilidade do jogador 1 ter uma peça (4).
Jogador 2: 1 peça na mão (4).
2 peças no jogo (4)
2 peças no jogo (4)
Monte de Compra: 13 peças
Jogador 1: 2 peças
Jogador 2: 1 peça
P12= C2, 1 x (4/15)^1 x (11/15)^1=39,11%

59. Probabilidade
• Probabilidade 13
Probabilidade do jogador 2 ter uma peça (4).
Jogador 1: 0 peça na mão (4).
Monte de Compra: 12 peças
Jogador 1: 3 peças
Jogador 2: 1 peça
P13= C1, 1 x (5/13)^1 x (8/13)^0=23,67%