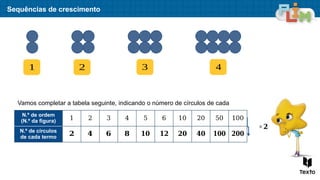
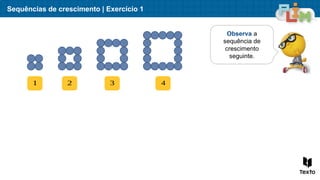
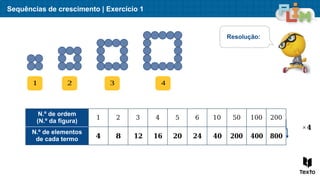
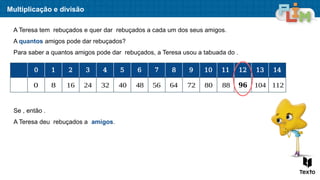
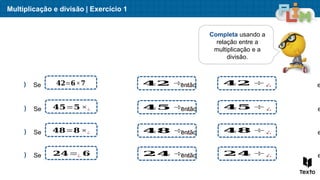
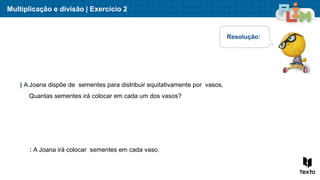
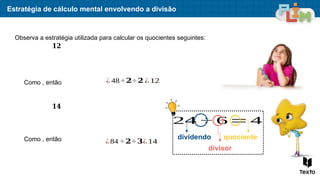
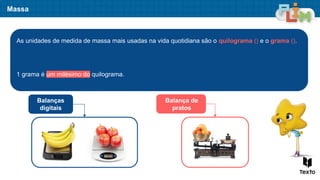
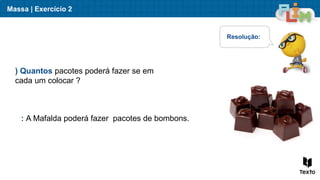
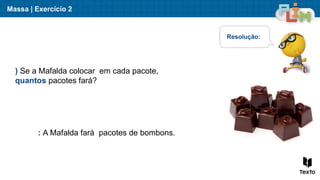
O documento aborda sequências de crescimento, ilustrando como cada figura representa um termo, e relaciona o número de elementos a sua ordem na sequência. São apresentados exercícios de multiplicação e divisão, enfatizando a relação entre esses conceitos e a resolução de problemas práticos. Além disso, discute medidas de massa, mostrando exemplos práticos da utilização de quilogramas e gramas.

1. Unidade 6
O que aprendi

2. Sequências
de crescimento
Sequências de crescimento

3. Numa sequência pictórica, cada figura corresponde a um termo da
sequência e cada termo tem uma ordem.
Numa sequência, a figura corresponde ao º termo da sequência, a
figura corresponde ao º termo, etc. Cada termo é formado por um
conjunto de elementos.
Sequências de crescimento
Uma sequência pictórica é
formada por desenhos ou
imagens.

4. Sequências de crescimento
Exemplo:
Observa a sequência de crescimento seguinte.
1 2 3 4
Neste caso, o número de círculos de cada figura é designado por termo da
sequência e a posição que cada figura ocupa na sequência é a ordem do termo.

5. Sequências de crescimento
1 2 3 4
 o primeiro termo ou termo de ordem é ;
 o segundo termo ou termo de ordem é ;
 o terceiro termo ou termo de ordem é ;
 o quarto termo ou termo de ordem é .
Se a sequência continuar a crescer da mesma forma, podemos afirmar que o
quinto termo será constituído por círculos.
𝟓×𝟐=𝟏𝟎

6. Sequências de crescimento
1 2 3 4
Vamos completar a tabela seguinte, indicando o número de círculos de cada
termo.
N.º de ordem
(N.º da figura) 1 2 3 4 5 6 10 20 50 100
N.º de círculos
de cada termo
𝟐 𝟒 𝟔 𝟖 𝟏𝟎 𝟏𝟐 𝟐𝟎 𝟒𝟎 𝟏𝟎𝟎 𝟐𝟎𝟎
×𝟐

7. Sequências de crescimento | Exercício 1
Observa a
sequência de
crescimento
seguinte.
1 2 3 4

8. Sequências de crescimento | Exercício 1
) Desenha o
º termo da
sequência.
1 2 3 4
Observa que cada termo tem a forma de um quadrado.

9. Sequências de crescimento | Exercício 1
) Quantos elementos
terá o º termo da
sequência? Explica as
tuas ideias.
1 2 3 4
Se observares a relação entre o número de elementos e o número de ordem do termo,
perceberás que o número de elementos de cada termo se obtém multiplicando por o número
de ordem desse termo.
Assim, o º termo da sequência será constituído por elementos.
𝟏𝟎×𝟒=𝟒𝟎

10. Sequências de crescimento | Exercício 1
) Completa a tabela
indicando o número de
elementos de cada um
dos termos.
1 2 3 4
N.º de ordem
(N.º da figura)
1 2 3 4 5 6 10 50 100 200
N.º de elementos
de cada termo

11. Sequências de crescimento | Exercício 1
1 2 3 4
N.º de ordem
(N.º da figura)
1 2 3 4 5 6 10 50 100 200
N.º de elementos
de cada termo
Resolução:
𝟒 𝟖 𝟏𝟐 𝟏𝟔 𝟐𝟎 𝟐𝟒 𝟒𝟎 𝟐𝟎𝟎 𝟒𝟎𝟎 𝟖𝟎𝟎
×𝟒

12. Sequências de crescimento | Exercício 1
) Qual será o número
da figura com
elementos? Explica
como pensaste.
1 2 3 4
A figura número será constituída por elementos.
𝟖𝟎÷𝟒=𝟐𝟎

13. Sequências de crescimento | Exercício 1
) Será possível que um
termo da sequência
tenha elementos?
Justifica.
1 2 3 4
Não é possível haver um termo da sequência com um número ímpar de elementos, pois o
número de elementos é sempre um múltiplo de .
Assim, o número de elementos de cada termo é sempre um número par, não existindo um
termo da sequência, por exemplo, com elementos.

14. Multiplicação e divisão
Multiplicação e divisão

15. Multiplicação e divisão
A Teresa tem rebuçados e quer dar rebuçados a cada um dos seus amigos.
A quantos amigos pode dar rebuçados?
Para saber a quantos amigos pode dar rebuçados, a Teresa usou a tabuada do .
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 8 16 24 32 40 48 56 64 72 80 88 𝟗𝟔 104 112
Se , então .
A Teresa deu rebuçados a amigos.

16. Multiplicação e divisão
Podemos usar a relação entre a multiplicação e a divisão para resolver problemas.
Exemplo:
6 × 3=18 18 ÷ 3=6 18 ÷ 6=3

17. Se então e
Se então e
Se então e
Multiplicação e divisão | Exercício 1
) Se então e
𝟒𝟐=𝟔×𝟕 𝟒𝟐 ÷ ¿ 𝟒𝟐 ÷ ¿
) 𝟒𝟓=𝟓 ׿ 𝟒𝟓 ÷ ¿ 𝟒𝟓 ÷ ¿
) 𝟒𝟖=𝟖 ׿ 𝟒𝟖 ÷ ¿ 𝟒𝟖 ÷ ¿
) 𝟐𝟒=¿ 𝟔 𝟐𝟒 ÷ ¿ 𝟐𝟒 ÷ ¿
Completa usando a
relação entre a
multiplicação e a
divisão.

18. Se então e
Se então e
Se então e
Multiplicação e divisão | Exercício 1
) Se então e
𝟒𝟐=𝟔×𝟕 𝟒𝟐 ÷ ¿ 𝟒𝟐 ÷ ¿
) 𝟒𝟓=𝟓 ׿ 𝟒𝟓 ÷ ¿ 𝟒𝟓 ÷ ¿
) 𝟒𝟖=𝟖 ׿ 𝟒𝟖 ÷ ¿ 𝟒𝟖 ÷ ¿
) 𝟐𝟒=¿ 𝟔 𝟐𝟒 ÷ ¿ 𝟐𝟒 ÷ ¿
Resolução:
6 7 7 6
5 9 9 5
8 6 6 8
4 6 6 4
9
6
4

19. Multiplicação e divisão | Exercício 2
Resolve os problemas
seguintes, usando a
relação entre a
multiplicação e a
divisão.
) Uma turma tem alunos.
Se a professora formar grupos de alunos, quantos grupos consegue formar?

20. Multiplicação e divisão | Exercício 2
) Uma turma tem alunos.
Se a professora formar grupos de alunos, quantos grupos consegue formar?
Resolução:
: A professora consegue formar grupos.

21. Multiplicação e divisão | Exercício 2
Resolve os problemas
seguintes, usando a
relação entre a
multiplicação e a
divisão.
) A Joana dispõe de sementes para distribuir equitativamente por vasos.
Quantas sementes irá colocar em cada um dos vasos?

22. Multiplicação e divisão | Exercício 2
) A Joana dispõe de sementes para distribuir equitativamente por vasos.
Quantas sementes irá colocar em cada um dos vasos?
Resolução:
: A Joana irá colocar sementes em cada vaso.

23. Estratégia de cálculo
mental envolvendo
a divisão
Estratégia de cálculo mental envolvendo a divisão

24. Estratégia de cálculo mental envolvendo a divisão
Observa a estratégia utilizada para calcular os quocientes seguintes:
Como , então ¿ 48÷ 𝟐÷ 𝟐 ¿ 12
𝟏𝟐
Como , então ¿84 ÷ 𝟐÷ 𝟑¿ 14
𝟏𝟒
24 ÷ 6= 4
dividendo
divisor
quociente

25. Estratégia de cálculo mental envolvendo a divisão | Exercício 1
Utiliza a mesma
estratégia e calcula
os quocientes
seguintes:
64÷ 𝟒=?
64 ÷ 𝟐=¿ ¿
¿¿ ÷ 𝟐=¿ ¿
64 ÷ 4=¿ ¿
52÷ 𝟒=?
52 ÷𝟐 =¿ ¿
¿¿ ÷ 𝟐=¿ ¿
52 ÷ 4 =¿ ¿
54÷ 𝟔=?
54 ÷ 𝟐=¿ ¿
¿¿ ÷ 𝟑=¿ ¿
54 ÷ 6 =¿ ¿
72÷𝟔=?
72 ÷𝟐 =¿ ¿
¿¿ ÷ 𝟑=¿ ¿
72 ÷ 6=¿ ¿

26. Estratégia de cálculo mental envolvendo a divisão | Exercício 1
64÷ 𝟒=?
64 ÷ 𝟐=¿ ¿
¿¿ ÷ 𝟐=¿ ¿
64 ÷ 4=¿ ¿
52÷ 𝟒=?
52 ÷𝟐 =¿ ¿
¿¿ ÷ 𝟐=¿ ¿
52 ÷ 4 =¿ ¿
54÷ 𝟔=?
54 ÷ 𝟐=¿ ¿
¿¿ ÷ 𝟑=¿ ¿
54 ÷ 6 =¿ ¿
72÷𝟔=?
72 ÷𝟐 =¿ ¿
¿¿ ÷ 𝟑=¿ ¿
72 ÷ 6=¿ ¿
Resolução:
32
32 16
𝟏𝟔
26
26 13
𝟏𝟑
27
27 9
𝟗
36
36 12
𝟏𝟐

27. Massa
Massa

28. Massa
As unidades de medida de massa mais usadas na vida quotidiana são o quilograma () e o grama ().
1 grama é um milésimo do quilograma.
Balanças
digitais
Balança de
pratos

29. Massa | Exercício 1
Completa a tabela assinalando com X a opção
que te parece mais adequada para determinar a
massa aproximada de cada objeto.
A medida
da massa
é…
menor do
que
maior do
que

30. Massa | Exercício 1
A medida
da massa
é…
menor do
que
maior do
que
Resolução:
X
X
X
X X

31. Massa | Exercício 2
Quantas unidades de cada
produto serão necessárias
para perfazer quilograma?
Lata de atum –
Resolução:
100g+100g+100g+100g+100g+100g+100g+100g+100g+100g=1000g=1kg
unidades

32. Massa | Exercício 2
Quantas unidades de cada
produto serão necessárias
para perfazer quilograma?
Fatias de queijo –
Resolução:
200 g+200g+200 g+200g+200 g=1000 g=1kg
unidades

33. Massa | Exercício 2
Quantas unidades de cada
produto serão necessárias
para perfazer quilograma?
Chocolate –
Resolução:
250 g+250 g +250 g+250 g=1000 g=1 kg
unidades

34. Massa | Exercício 2
AMafaldacomprou1kgdebombonsepretendefazerpacotesmaispequenosparaofereceraosamigos.
) Quantos pacotes poderá fazer se em
cada um colocar ?

35. Massa | Exercício 2
) Quantos pacotes poderá fazer se em
cada um colocar ?
Resolução:
: A Mafalda poderá fazer pacotes de bombons.

36. Massa | Exercício 2
AMafaldacomprou1kgdebombonsepretendefazerpacotesmaispequenosparaofereceraosamigos.
) Se a Mafalda colocar em cada pacote,
quantos pacotes fará?

37. Massa | Exercício 2
) Se a Mafalda colocar em cada pacote,
quantos pacotes fará?
Resolução:
: A Mafalda fará pacotes de bombons.

38. Massa | Exercício 2
AMafaldacomprou1kgdebombonsepretendefazerpacotesmaispequenosparaofereceraosamigos.
) Se a Mafalda der um pacote de bombons
de a cada um dos seus amigos, quantos
quilogramas de bombons terá de comprar?

39. Massa | Exercício 2
Resolução:
Com de bombons, a Mafalda poderá fazer
pacotes de bombons.
Como , tem-se que .
) Se a Mafalda der um pacote de bombons
de a cada um dos seus amigos, quantos
quilogramas de bombons terá de comprar?
: A Mafalda terá que comprar de bombons.