O documento apresenta os resultados de três problemas resolvidos utilizando o método numérico de Runge-Kutta de 4a ordem para sistemas de equações diferenciais ordinárias. Os problemas tratam da validação do método, da resolução de um circuito elétrico RLC e de outro sistema de equações. As soluções numéricas são comparadas com as soluções exatas quando fornecidas e os resultados são apresentados em tabelas e gráficos.

1. UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO
CENTRO TECNOLÓGICO
ENGENHARIA ELÉTRICA
ANA LUIZA CÔRTE E MAURO LUIZ PEDRONI JUNIOR
TRABALHO COMPUTACIONAL DE
ALGORITMOS NUMÉRICOS – RELATÓRIO
Vitória
Dezembro de 2016

2. UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO
ANA LUIZA CÔRTE E MAURO LUIZ PEDRONI JUNIOR
TRABALHO COMPUTACIONAL DE
ALGORITMOS NUMÉRICOS – RELATÓRIO
Vitória
Dezembro de 2016
Relatório apresentado à
professora Cláudia Galarda
Varassin como parte integrante do
trabalho computacional da
disciplina de algoritmos numéricos
do curso de Engenharia Elétrica

3. SUMÁRIO
INTRODUÇÃO........................................................................................... 4
MÉTODO NUMÉRICO............................................................................... 5
PROBLEMAS TRATADOS ....................................................................... 6
PROBLEMA 1......................................................................................... 6
PROBLEMA 2......................................................................................... 6
PROBLEMA 3......................................................................................... 6
RESULTADOS .......................................................................................... 8
PROBLEMA 1......................................................................................... 8
PROBLEMA 2....................................................................................... 10
PROBLEMA 3....................................................................................... 12
CÓDIGO .................................................................................................. 17
ANEXO I – CÓDIGO MATLAB PARA PROBLEMA 1 ............................ 20
ANEXO II – CÓDIGO MATLAB PARA PROBLEMA 2 ........................... 21
ANEXO III – CÓDIGO MATLAB PARA PROBLEMA 3 .......................... 22
BIBLIOGRAFIA....................................................................................... 23

4. LISTA DE FIGURAS
Figura 1: circuito elétrico proposto............................................................. 7
Figura 2: Gráfico comparativo entre y1 exata e y1 calculada .................... 9
Figura 3: Gráfico comparativo entre y2 exata e y2 calculada .................. 10
Figura 4: Gráfico da solução y1 e y2 para m=20 ..................................... 12
Figura 5: Gráfico da solução numérica para m=100 ................................ 16
LISTA DE TABELAS
Tabela 1: Solução para m=5...................................................................... 8
Tabela 2: Solução para m=5...................................................................... 9
Tabela 3: Solução para m=5.................................................................... 11
Tabela 4: Solução para m=20.................................................................. 11
Tabela 5: Solução para m=30.................................................................. 13
Tabela 6: Solução para m=100................................................................ 15

5. 4
INTRODUÇÃO
Equações diferenciais ordinárias (EDO) são muito utilizadas na
modelagem de modelos matemáticos. Há vários métodos que resolvem
analiticamente uma EDO, entretanto nem sempre é possível obter uma solução
analítica. Neste caso, os métodos numéricos são uma saída para se encontrar
uma solução aproximada.
O trabalho tem como objetivo a resolução de um conjunto de equações
diferenciais ordinárias, chamada de sistema de equações. O método aplicado
aqui foi o de Rungue Kutta de 4ª ordem em que a partir de valores inicias foi
obtido o resultado aproximado de um sistema de EDOs de primeira ordem.
Para isso desenvolveu-se um programa em linguagem C que resolve 3
exercícios (sistemas) diferentes.

6. 5
MÉTODO NUMÉRICO
O método utilizado nesse trabalho é bem simples. Basta estender o
método de Runge Kutta de 4ª ordem utilizado para solução de EDOs. Com
esse método calculam-se as aproximações para os valores de y1(x) e y2(x) de
forma sincronizada a partir de valores iniciais quaisquer de y1 e y2. A cada
discretização novos valores de y1(i+1) e y2(i+1) a partir de valores anteriores
de y1 (y1(i)) e y2 (y1(i)). Abaixo estão as equações utilizadas para o cálculo da
solução aproximada do sistema de equações.
𝑦1(𝑖 + 1) = 𝑦1(𝑖) +
ℎ
6
∗ (𝑘11 + 2𝑘21 + 2𝑘31 + 𝑘41)
𝑦2(𝑖 + 1) = 𝑦2(𝑖) +
ℎ
6
∗ (𝑘12 + 2𝑘22 + 2𝑘32 + 𝑘42)
Os valores de k11, k21, k31, k41 e k12, k22, k32, k42 representam as
declividades de y1 e y2, respectivamente.
𝑘11 = 𝑓1(𝑥(𝑖), 𝑦1(𝑖), 𝑦2(𝑖))
𝑘21 = 𝑓1(𝑥(𝑖) +
ℎ
2
, 𝑦1(𝑖) + ℎ(𝑘11)/2, 𝑦2(𝑖) + ℎ(𝑘12)/2)
𝑘31 = 𝑓1(𝑥(𝑖) +
ℎ
2
, 𝑦1(𝑖) + ℎ(𝑘21)/2, 𝑦2(𝑖) + ℎ(𝑘22)/2)
𝑘41 = 𝑓1(𝑥(𝑖) + ℎ, 𝑦1(𝑖) + ℎ𝑘31, 𝑦2(𝑖) + ℎ𝑘32)
𝑘12 = 𝑓2(𝑥(𝑖), 𝑦1(𝑖), 𝑦2(𝑖))
𝑘22 = 𝑓2(𝑥(𝑖) +
ℎ
2
, 𝑦1(𝑖) + ℎ(𝑘11)/2, 𝑦2(𝑖) + ℎ(𝑘12)/2)
𝑘32 = 𝑓2(𝑥(𝑖) +
ℎ
2
, 𝑦1(𝑖) + ℎ(𝑘21)/2, 𝑦2(𝑖) + ℎ(𝑘22)/2)
𝑘42 = 𝑓2(𝑥(𝑖) + ℎ, 𝑦1(𝑖) + ℎ𝑘31, 𝑦2(𝑖) + ℎ𝑘32)

7. 6
PROBLEMAS TRATADOS
 PROBLEMA 1
O problema 1 é chamado “problema da validação” pois as
equações exatas foram fornecidas para a comparação dos
resultados obtidos. O exercício fornece o seguinte sistema de
equações diferenciais e valores iniciais para Y.
{
𝑦′
1
= 𝑓1(𝑥, 𝑦1, 𝑦2) = 𝑦2
𝑦′
2
= 𝑓2(𝑥, 𝑦1, 𝑦2) = 2𝑦1 + 𝑦2 − 𝑥2
𝑦1(0.0) = 1.0
𝑦2(0.0) = 0.0
O domínio no qual o sistema será calculado é 𝐷 = [0.0, 1.0], com
𝑚 = 5 e 𝑚 = 20.
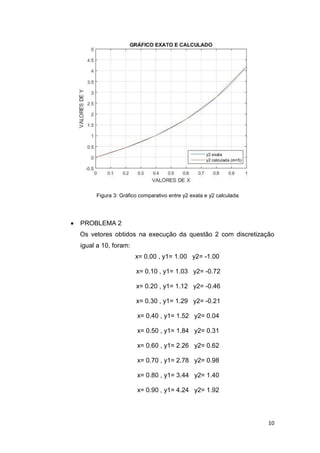
A questão solicita ainda que sejam traçadas em um mesmo plano
de par de eixos cartesianos, a solução numérica 𝑦1 obtida com
𝑚 = 5 e a solução 𝑦1 exata. Da mesma maneira, deve-se traçar a
solução numérica 𝑦2 obtida com 𝑚 = 5 e a solução 𝑦2 exata.
As soluções exatas fornecidas são:
𝑦1, 𝑒𝑥𝑎𝑡𝑎 = 0.25(𝑒2𝑥
+ 2𝑥2
− 2𝑥 + 3)
𝑦2, 𝑒𝑥𝑎𝑡𝑎 = 𝑦′
1
 PROBLEMA 2
O problema 2 fornece o seguinte sistema de equações diferenciais
e valores iniciais para Y.
{
𝑦′
1
= 𝑓1(𝑥, 𝑦1, 𝑦2) = 𝑦1 + 𝑦2 + 3𝑥
𝑦′
2
= 𝑓2(𝑥, 𝑦1, 𝑦2) = 2𝑦1 − 𝑦2 − 𝑥
𝑦1(0.0) = 1.0
𝑦2(0.0) = −1.0
O domínio no qual o sistema será calculado é 𝐷 = [0.0, 1.0], com
𝑚 = 10 e 𝑚 = 20.
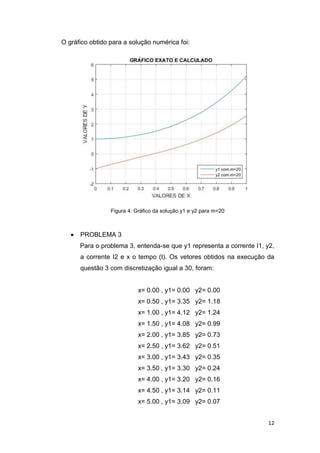
A questão solicita que sejam traçadas em um plano de par de eixos
cartesianos, as soluções numéricas obtidas com 𝑚 = 20.
 PROBLEMA 3
O problema 3 fornece o seguinte circuito RLC abaixo:

8. 7
Figura 1: circuito elétrico proposto
As correntes 𝐼1 e 𝐼2 são observadas na malha esquerda e direita do
circuito, respectivamente. Usando a Lei de Tensão de Kirchoff, é
possível traçar o seguinte modelo matemático para o circuito:
{
𝐼′
1 = 12 − 4𝐼1 + 4𝐼2
𝐼′
2 = 4.8 − 1.6𝐼1 + 𝐼2
Supõem-se que as cargas e as correntes são nulas quando a
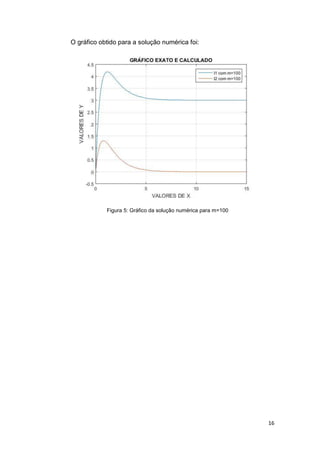
chave é fechada no instante 𝑡 = 0. A questão solicita que sejam
obtidos os valores de 𝐼1(𝑡) e 𝐼2(𝑡) para t no intervalo 𝐼 = [0, 𝑡final] e
𝑡final = 15 e m = 30 e m = 100. Além disso, a questão ainda solicita
que seja traçado o gráfico das correntes.

9. 8
RESULTADOS
 PROBLEMA 1
Os vetores obtidos na execução da questão 1 com discretização
igual a 5, foram:
x= 0.00 , y1= 1.00 y2= 0.00
x= 0.20 , y1= 1.04 y2= 0.45
x= 0.40 , y1= 1.19 y2= 1.01
x= 0.60 , y1= 1.46 y2= 1.76
x= 0.80 , y1= 1.91 y2= 2.78
x= 1.00 , y1= 2.60 y2= 4.19
Tabela 1: Solução para m=5
Os vetores obtidos na execução da questão 1 com discretização
igual a 20, foram:
x= 0.00 , y1= 1.00 y2= 0.00
x= 0.05 , y1= 1.00 y2= 0.10
x= 0.10 , y1= 1.01 y2= 0.21
x= 0.15 , y1= 1.02 y2= 0.32
x= 0.20 , y1= 1.04 y2= 0.45
x= 0.25 , y1= 1.07 y2= 0.57
x= 0.30 , y1= 1.10 y2= 0.71
x= 0.35 , y1= 1.14 y2= 0.86
x= 0.40 , y1= 1.19 y2= 1.01
x= 0.45 , y1= 1.24 y2= 1.18
x= 0.50 , y1= 1.30 y2= 1.36
x= 0.55 , y1= 1.38 y2= 1.55
x= 0.60 , y1= 1.46 y2= 1.76

10. 9
x= 0.65 , y1= 1.55 y2= 1.98
x= 0.70 , y1= 1.66 y2= 2.23
x= 0.75 , y1= 1.78 y2= 2.49
x= 0.80 , y1= 1.91 y2= 2.78
x= 0.85 , y1= 2.05 y2= 3.09
x= 0.90 , y1= 2.22 y2= 3.42
x= 0.95 , y1= 2.40 y2= 3.79
x= 1.00 , y1= 2.60 y2= 4.19
Tabela 2: Solução para m=5
O gráfico obtido para 𝑦1 foi:
Figura 2: Gráfico comparativo entre y1 exata e y1 calculada

11. 10
Figura 3: Gráfico comparativo entre y2 exata e y2 calculada
 PROBLEMA 2
Os vetores obtidos na execução da questão 2 com discretização
igual a 10, foram:
x= 0.00 , y1= 1.00 y2= -1.00
x= 0.10 , y1= 1.03 y2= -0.72
x= 0.20 , y1= 1.12 y2= -0.46
x= 0.30 , y1= 1.29 y2= -0.21
x= 0.40 , y1= 1.52 y2= 0.04
x= 0.50 , y1= 1.84 y2= 0.31
x= 0.60 , y1= 2.26 y2= 0.62
x= 0.70 , y1= 2.78 y2= 0.98
x= 0.80 , y1= 3.44 y2= 1.40
x= 0.90 , y1= 4.24 y2= 1.92

12. 11
x= 1.00 , y1= 5.22 y2= 2.54
Tabela 3: Solução para m=5
Os vetores obtidos na execução da questão 2 com discretização
igual a 20, foram:
x= 0.00 , y1= 1.00 y2= -1.00
x= 0.05 , y1= 1.01 y2= -0.85
x= 0.10 , y1= 1.03 y2= -0.72
x= 0.15 , y1= 1.07 y2= -0.59
x= 0.20 , y1= 1.12 y2= -0.46
x= 0.25 , y1= 1.20 y2= -0.33
x= 0.30 , y1= 1.29 y2= -0.21
x= 0.35 , y1= 1.39 y2= -0.09
x= 0.40 , y1= 1.52 y2= 0.04
x= 0.45 , y1= 1.67 y2= 0.17
x= 0.50 , y1= 1.84 y2= 0.31
x= 0.55 , y1= 2.04 y2= 0.46
x= 0.60 , y1= 2.26 y2= 0.62
x= 0.65 , y1= 2.50 y2= 0.79
x= 0.70 , y1= 2.78 y2= 0.98
x= 0.75 , y1= 3.09 y2= 1.18
x= 0.80 , y1= 3.44 y2= 1.40
x= 0.85 , y1= 3.82 y2= 1.65
x= 0.90 , y1= 4.24 y2= 1.92
x= 0.95 , y1= 4.70 y2= 2.22
x= 1.00 , y1= 5.22 y2= 2.54
Tabela 4: Solução para m=20

13. 12
O gráfico obtido para a solução numérica foi:
Figura 4: Gráfico da solução y1 e y2 para m=20
 PROBLEMA 3
Para o problema 3, entenda-se que y1 representa a corrente I1, y2,
a corrente I2 e x o tempo (t). Os vetores obtidos na execução da
questão 3 com discretização igual a 30, foram:
x= 0.00 , y1= 0.00 y2= 0.00
x= 0.50 , y1= 3.35 y2= 1.18
x= 1.00 , y1= 4.12 y2= 1.24
x= 1.50 , y1= 4.08 y2= 0.99
x= 2.00 , y1= 3.85 y2= 0.73
x= 2.50 , y1= 3.62 y2= 0.51
x= 3.00 , y1= 3.43 y2= 0.35
x= 3.50 , y1= 3.30 y2= 0.24
x= 4.00 , y1= 3.20 y2= 0.16
x= 4.50 , y1= 3.14 y2= 0.11
x= 5.00 , y1= 3.09 y2= 0.07

14. 13
x= 5.50 , y1= 3.06 y2= 0.05
x= 6.00 , y1= 3.04 y2= 0.03
x= 6.50 , y1= 3.03 y2= 0.02
x= 7.00 , y1= 3.02 y2= 0.01
x= 7.50 , y1= 3.01 y2= 0.01
x= 8.00 , y1= 3.01 y2= 0.01
x= 8.50 , y1= 3.01 y2= 0.00
x= 9.00 , y1= 3.00 y2= 0.00
x= 9.50 , y1= 3.00 y2= 0.00
x= 10.00 , y1= 3.00 y2= 0.00
x= 10.50 , y1= 3.00 y2= 0.00
x= 11.00 , y1= 3.00 y2= 0.00
x= 11.50 , y1= 3.00 y2= 0.00
x= 12.00 , y1= 3.00 y2= 0.00
x= 12.50 , y1= 3.00 y2= 0.00
x= 13.00 , y1= 3.00 y2= 0.00
x= 13.50 , y1= 3.00 y2= 0.00
x= 14.00 , y1= 3.00 y2= 0.00
x= 14.50 , y1= 3.00 y2= 0.00
x= 15.00 , y1= 3.00 y2= 0.00
Tabela 5: Solução para m=30
Os vetores obtidos na execução da questão 3 com discretização
igual a 100, foram:
x= 0.00 , y1= 0.00 y2= 0.00
x= 0.15 , y1= 1.51 y2= 0.58
x= 0.30 , y1= 2.54 y2= 0.95
x= 0.45 , y1= 3.24 y2= 1.16
x= 0.60 , y1= 3.68 y2= 1.27
x= 0.75 , y1= 3.96 y2= 1.30
x= 0.90 , y1= 4.11 y2= 1.29
x= 1.05 , y1= 4.18 y2= 1.24
x= 1.20 , y1= 4.19 y2= 1.17
x= 1.35 , y1= 4.16 y2= 1.09
x= 1.50 , y1= 4.11 y2= 1.01
x= 1.65 , y1= 4.04 y2= 0.92
x= 1.80 , y1= 3.97 y2= 0.84

15. 14
x= 1.95 , y1= 3.89 y2= 0.76
x= 2.10 , y1= 3.81 y2= 0.69
x= 2.25 , y1= 3.74 y2= 0.62
x= 2.40 , y1= 3.67 y2= 0.55
x= 2.55 , y1= 3.60 y2= 0.50
x= 2.70 , y1= 3.54 y2= 0.44
x= 2.85 , y1= 3.48 y2= 0.40
x= 3.00 , y1= 3.43 y2= 0.35
x= 3.15 , y1= 3.39 y2= 0.31
x= 3.30 , y1= 3.35 y2= 0.28
x= 3.45 , y1= 3.31 y2= 0.25
x= 3.60 , y1= 3.27 y2= 0.22
x= 3.75 , y1= 3.24 y2= 0.20
x= 3.90 , y1= 3.22 y2= 0.17
x= 4.05 , y1= 3.19 y2= 0.16
x= 4.20 , y1= 3.17 y2= 0.14
x= 4.35 , y1= 3.15 y2= 0.12
x= 4.50 , y1= 3.14 y2= 0.11
x= 4.65 , y1= 3.12 y2= 0.10
x= 4.80 , y1= 3.11 y2= 0.09
x= 4.95 , y1= 3.09 y2= 0.08
x= 5.10 , y1= 3.08 y2= 0.07
x= 5.25 , y1= 3.07 y2= 0.06
x= 5.40 , y1= 3.07 y2= 0.05
x= 5.55 , y1= 3.06 y2= 0.05
x= 5.70 , y1= 3.05 y2= 0.04
x= 5.85 , y1= 3.05 y2= 0.04
x= 6.00 , y1= 3.04 y2= 0.03
x= 6.15 , y1= 3.04 y2= 0.03
x= 6.30 , y1= 3.03 y2= 0.03
x= 6.45 , y1= 3.03 y2= 0.02
x= 6.60 , y1= 3.03 y2= 0.02
x= 6.75 , y1= 3.02 y2= 0.02
x= 6.90 , y1= 3.02 y2= 0.02
x= 7.05 , y1= 3.02 y2= 0.01
x= 7.20 , y1= 3.02 y2= 0.01
x= 7.35 , y1= 3.01 y2= 0.01
x= 7.50 , y1= 3.01 y2= 0.01
x= 7.65 , y1= 3.01 y2= 0.01
x= 7.80 , y1= 3.01 y2= 0.01
x= 7.95 , y1= 3.01 y2= 0.01
x= 8.10 , y1= 3.01 y2= 0.01
x= 8.25 , y1= 3.01 y2= 0.01
x= 8.40 , y1= 3.01 y2= 0.00
x= 8.55 , y1= 3.01 y2= 0.00
x= 8.70 , y1= 3.00 y2= 0.00
x= 8.85 , y1= 3.00 y2= 0.00
x= 9.00 , y1= 3.00 y2= 0.00

16. 15
x= 9.15 , y1= 3.00 y2= 0.00
x= 9.30 , y1= 3.00 y2= 0.00
x= 9.45 , y1= 3.00 y2= 0.00
x= 9.60 , y1= 3.00 y2= 0.00
x= 9.75 , y1= 3.00 y2= 0.00
x= 9.90 , y1= 3.00 y2= 0.00
x= 10.05 , y1= 3.00 y2= 0.00
x= 10.20 , y1= 3.00 y2= 0.00
x= 10.35 , y1= 3.00 y2= 0.00
x= 10.50 , y1= 3.00 y2= 0.00
x= 10.65 , y1= 3.00 y2= 0.00
x= 10.80 , y1= 3.00 y2= 0.00
x= 10.95 , y1= 3.00 y2= 0.00
x= 11.10 , y1= 3.00 y2= 0.00
x= 11.25 , y1= 3.00 y2= 0.00
x= 11.40 , y1= 3.00 y2= 0.00
x= 11.55 , y1= 3.00 y2= 0.00
x= 11.70 , y1= 3.00 y2= 0.00
x= 11.85 , y1= 3.00 y2= 0.00
x= 12.00 , y1= 3.00 y2= 0.00
x= 12.15 , y1= 3.00 y2= 0.00
x= 12.30 , y1= 3.00 y2= 0.00
x= 12.45 , y1= 3.00 y2= 0.00
x= 12.60 , y1= 3.00 y2= 0.00
x= 12.75 , y1= 3.00 y2= 0.00
x= 12.90 , y1= 3.00 y2= 0.00
x= 13.05 , y1= 3.00 y2= 0.00
x= 13.20 , y1= 3.00 y2= 0.00
x= 13.35 , y1= 3.00 y2= 0.00
x= 13.50 , y1= 3.00 y2= 0.00
x= 13.65 , y1= 3.00 y2= 0.00
x= 13.80 , y1= 3.00 y2= 0.00
x= 13.95 , y1= 3.00 y2= 0.00
x= 14.10 , y1= 3.00 y2= 0.00
x= 14.25 , y1= 3.00 y2= 0.00
x= 14.40 , y1= 3.00 y2= 0.00
x= 14.55 , y1= 3.00 y2= 0.00
x= 14.70 , y1= 3.00 y2= 0.00
x= 14.85 , y1= 3.00 y2= 0.00
x= 15.00 , y1= 3.00 y2= 0.00
Tabela 6: Solução para m=100

17. 16
O gráfico obtido para a solução numérica foi:
Figura 5: Gráfico da solução numérica para m=100

18. 17
CÓDIGO
//Trabalho de algoritmos numéricos
- Ana Luiza Côrte e Mauro Pedroni
//Acesso às bibliotecas
#include<stdio.h>
#include<math.h>
#define Max 100
// Indica as funcoes
float f1(float x, float y1, float y2, int
e)
{
float der1;
// --- Problema 1
if (e==1)
{
der1 = y2;
}
// ---- Problema 2
if (e==2)
{
der1 = y1 + y2 + (3 * x);
}
// ---- Problema 3
if (e==3)
{
der1 = 12 - (4 * y1) + (4 * y2);
}
return(der1);
}
float f2(float x, float y1, float y2,
int e)
{
float der2;
// --- Problema 1
if (e==1)
{
der2 = (2 * y1) + y2 - (x*x);
}
// ---- Problema 2
if (e==2)
{
der2 = (2 * y1) - y2 - x;
}
// ---- Problema 3
if (e==3)
{
der2= 4.8 - (1.6*y1) +
(1.2*y2);
}

19. 18
return(der2);
}
// Main -------------------------------
int main(){
float x[Max], y1[Max], y2[Max],
a, b, y1a, y2a, h, k11[Max],
k21[Max], k31[Max], k41[Max],
k12[Max], k22[Max], k32[Max],
k42[Max];
int m, i, e = 0;
while(e!=1||e!=2||e!=3||e!=4)
{
// Menu
printf("nDigite uma opção:nn
1 - Resolver o problema 1 (o
exemplo da validação).nn 2 -
Resolver o problema 2.nn 3 -
Resolver o problema do circuito
elétrico. nn 4 - SairnnEscolha:");
scanf("%d", &e);
if ((e==1)||(e==2)||(e==3))
{
// Dados de entrada
printf("nDigite a:");
scanf("%f", &a);
printf("nDigite b:");
scanf("%f", &b);
printf("nDigite y1(a):");
scanf("%f", &y1a);
printf("nDigite y2(a):");
scanf("%f", &y2a);
printf("nDigite o tamanho da
discretização desejada (m):n");
scanf("%d", &m);
// Calcular o tamanho do
passo
h = (b - a) / m;
// Valor inicial de X
x[0] = a;
for (i = 0; i < m; i++)
{
x[i + 1] = x[i] + h;
}
// Valores iniciais
y1[0] = y1a;
y2[0] = y2a;
// Obtendo a solução
numérica
// Cálculo dos Ks e seus
argumentos
for (i = 0; i < m; i++)
{
k11[i] = f1(x[i], y1[i], y2[i], e);

20. 19
k12[i] = f2(x[i], y1[i], y2[i], e);
float xnext1 = x[i] + (h / 2);
float xnext2 = x[i] + h;
float y1next1 = y1[i] + (h*(k11[i] / 2));
float y2next1 = y2[i] + (h*(k12[i] / 2));
k21[i] = f1(xnext1, y1next1, y2next1,
e);
k22[i] = f2(xnext1, y1next1, y2next1,
e);
float y1next2 = y1[i] + (h*(k21[i] / 2));
float y2next2 = y2[i] + (h*(k22[i] / 2));
k31[i] = f1(xnext1, y1next2, y2next2,
e);
k32[i] = f2(xnext1, y1next2, y2next2,
e);
float y1next3 = y1[i] + (h*(k31[i]));
float y2next3 = y2[i] + (h*(k32[i]));
k41[i] = f1(xnext2, y1next3, y2next3,
e);
k42[i] = f2(xnext2, y1next3, y2next3,
e);
// Cálculo dos Ys
y1[i+1]=(y1[i]+((h/6)*(k11[i]+(2*k21[i]
)+(2*k31[i])+k41[i])));
y2[i+1]=(y2[i]+((h/6)*(k12[i]+(2*k22[i]
)+(2*k32[i])+k42[i])));
}
// Mostrando os valores calculados
printf("nOs vetores calculados
são:n");
for (i = 0; i <= m; i++)
{
printf(" x= %.2f , y1= %.2f y2= %.2f
nn", x[i], y1[i], y2[i]);
}
printf(" ----------------------n");
}
else if (e==4)
{
return(0);
}
else
{
printf("nOpção inválidan");
}
}

21. 20
ANEXO I – CÓDIGO MATLAB PARA PROBLEMA 1
% Desenha gráfico exato de y1
x=-0:.0001:1;
y1 = 0.25*(exp(2*x) + 2*(x.^2) - 2*x
+ 3);
plot(x,y1);
axis ([0 1 0.95 2.65]);
xlabel('VALORES DE X')
ylabel('VALORES DE Y')
title('GRÁFICO EXATO E
CALCULADO')
grid on;
hold on;
% Desenha gráfico obtido de y1
xo=[0.00 0.20 0.40 0.60 0.80 1.00];
y1o=[1.00 1.04 1.19 1.46 1.91 2.60];
plot(xo,y1o);
legend('y1 exata', 'y1 calculada
(m=5)');
% Desenha gráfico exato de y2
figure;
y2 = 0.25*((2*exp(2*x)) + 4*x - 2);
plot(x,y2);
axis ([0 1 -0.5 5]);
xlabel('VALORES DE X')
ylabel('VALORES DE Y')
title('GRÁFICO EXATO E
CALCULADO')
grid on;
hold on;
% Desenha gráfico obtido de y2
y2o=[0.00 0.45 1.01 1.76 2.78 4.19];
plot(xo,y2o);
legend('y2 exata', 'y2 calculada
(m=5)');

22. 21
ANEXO II – CÓDIGO MATLAB PARA PROBLEMA 2
% Desenha gráfico obtido de y1 e y2
xo=[0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70
0.75 0.80 0.85 0.90 0.95 1.00];
y1o=[1.00 1.01 1.03 1.07 1.12 1.20 1.29 1.39 1.52 1.67 1.84 2.04 2.26 2.50
2.78 3.09 3.44 3.82 4.24 4.70 5.22];
y2o=[-1.00 -0.85 -0.72 -0.59 -0.46 -0.33 -0.21 -0.09 0.04 0.17 0.31 0.46 0.62
0.79 0.98 1.18 1.40 1.65 1.92 2.22 2.54];
plot(xo,y1o);
axis ([0 1 -2 6]);
xlabel('VALORES DE X')
ylabel('VALORES DE Y')
title('GRÁFICO EXATO E CALCULADO')
grid on;
hold on;
plot(xo,y2o);
legend('y1 com m=20', 'y2 com m=20');

23. 22
ANEXO III – CÓDIGO MATLAB PARA PROBLEMA 3
% Desenha gráfico obtido de y1 e
y2
xo=[0.00 0.15 0.30 0.45 0.60 0.75
0.90 1.05 1.20 1.35 1.50 1.65 1.80
1.95 2.10 2.25 2.40 2.55 2.70 2.85
3.00 3.15 3.30 3.45 3.60 3.75 3.90
4.05 4.20 4.35 4.50 4.65 4.80 4.95
5.10 5.25 5.40 5.55 5.70 5.85 6.00
6.15 6.30 6.45 6.60 6.75 6.90 7.05
7.20 7.35 7.50 7.65 7.80 7.95 8.10
8.25 8.40 8.55 8.70 8.85 9.00 9.15
9.30 9.45 9.60 9.75 9.90 10.05
10.20 10.35 10.50 10.65 10.80
10.95 11.10 11.25 11.40 11.55
11.70 11.85 12.00 12.15 12.30
12.45 12.60 12.75 12.90 13.05
13.20 13.35 13.50 13.65 13.80
13.95 14.10 14.25 14.40 14.55
14.70 14.85 15.00];
y1o=[0.00 1.51 2.54 3.24 3.68 3.96
4.11 4.18 4.19 4.16 4.11 4.04 3.97
3.89 3.81 3.74 3.67 3.60 3.54 3.48
3.43 3.39 3.35 3.31 3.27 3.24 3.22
3.19 3.17 3.15 3.14 3.12 3.11 3.09
3.08 3.07 3.07 3.06 3.05 3.05 3.04
3.04 3.03 3.03 3.03 3.02 3.02 3.02
3.02 3.01 3.01 3.01 3.01 3.01 3.01
3.01 3.01 3.01 3.00 3.00 3.00 3.00
3.00 3.00 3.00 3.00 3.00 3.00 3.00
3.00 3.00 3.00 3.00 3.00 3.00 3.00
3.00 3.00 3.00 3.00 3.00 3.00 3.00
3.00 3.00 3.00 3.00 3.00 3.00 3.00
3.00 3.00 3.00 3.00 3.00 3.00 3.00
3.00 3.00 3.00 3.00];
y2o=[0.00 0.58 0.95 1.16 1.27 1.30
1.29 1.24 1.17 1.09 1.01 0.92 0.84
0.76 0.69 0.62 0.55 0.50 0.44 0.40
0.35 0.31 0.28 0.25 0.22 0.20 0.17
0.16 0.14 0.12 0.11 0.10 0.09 0.08
0.07 0.06 0.05 0.05 0.04 0.04 0.03
0.03 0.03 0.02 0.02 0.02 0.02 0.01
0.01 0.01 0.01 0.01 0.01 0.01 0.01
0.01 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00];
plot(xo,y1o);
axis ([0 15 -0.5 4.5]);
xlabel('VALORES DE X')
ylabel('VALORES DE Y')
title('GRÁFICO EXATO E
CALCULADO')
grid on;
hold on;
plot(xo,y2o);
legend('I1 com m=100', 'I2 com
m=100');

24. 23
BIBLIOGRAFIA
PDF da descrição do trabalho computacional
Rafael Barbosa. “Sistemas de Equações Diferenciais: Método de Euler e
Método de Runge Kutta de 4ª ordem”