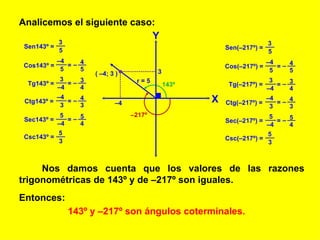
O documento discute ângulos coterminais, especificamente que os ângulos 143° e -217° são coterminais porque as razões trigonométricas de ambos os ângulos são iguais. Isso ocorre porque eles diferem em um múltiplo de 360°, portanto representam a mesma posição no círculo trigonométrico.

1. ÁNGULOS COTERMIINALES

2. Analicemos el siguiente caso: ( –4; 3 ) 3 – 4 143º – 217º Sen143º = Cos143º = Tg143º = Ctg143º = Sec143º = Csc143º = r = 5 Sen(–217º) = Cos(–217º) = Tg(–217º) = Ctg(–217º) = Sec(–217º) = Csc(–217º) = Nos damos cuenta que los valores de las razones trigonométricas de 143º y de –217º son iguales. Entonces: 143º y –217º son ángulos coterminales. X Y 5 3 = 4 5 – 5 – 4 = 3 4 – – 4 3 = 4 3 – 3 – 4 = 5 4 – – 4 5 3 5 5 3 = 4 5 – 5 – 4 = 3 4 – – 4 3 = 4 3 – 3 – 4 = 5 4 – – 4 5 3 5