Medidas eletricas prof_marcus_vinicius

Universidade Federal do Rio Grande do Norte
Centro de Tecnologia
Departamento de Engenharia Elétrica
Apostila de Medidas Elétricas
Marcus Vinicius Araújo Fernandes
Natal/RN - Brasil
Semestre 2008.1

Cap´ıtulo 1
Generalidades sobre os Instrumentos
de Medidas Elétricas
1.1 Defini¸cão de Medida
Medida é um processo de compara¸cão de grandezas de mesma espécie, ou seja, que
possuem um padrão único e comum entre elas. Duas grandezas de mesma espécie possuem
a mesma dimensão.
No processo de medida, a grande que serve de compara¸cão é denominada de “grandeza
unitária”ou “padrão unitário”.
As grandezas f´ısicas são englobadas em duas categorias:
a. Grandezas fundamentais (comprimento, tempo, etc.).
Grandezas Fundamentais
Grandeza Unidade Simbologia
Comprimento metro [m]
Massa quilograma [kg]
Tempo segundo [s]
Intensidade de Corrente ampéres [A]
Temperatura Termodinâmica kelvin [K]
Quantidade de Matéria mole [mol]
Intensidade Luminosa candela [cd]
b. Grandezas derivadas (velocidade, acelera¸cão, etc.).

Cap´ıtulo 1. Generalidades sobre os Instrumentos de Medidas Elétricas 2
Grandezas Elétricas Derivadas
Grandeza Derivada Unidade Dimensão Simbologia
Carga coulomb [A · s] [C]
Energia joule [m2
· kg · s−2
] [J]
Potência watt [m2
· kg · s−3
] [W]
Tensão volt [m2
· kg · s−3
· A−1
] [V ]
Resistência ohm [m2
· kg · s−3
· A−2
] [Ω]
Condutância siemens [m−2
· kg−1
· s3
· A2
] [S]
Capacitância farad [m−2
· kg−1
· s4
· A2
] [F]
Indutância henri [m2
· kg · s−2
· A−2
] [H]
Freqüência hertz [s−1
] [Hz]
1.2 Sistema de unidades
É um conjunto de defini¸cões que reúne de forma completa, coerente e concisa todas
as grandezas f´ısicas fundamentais e derivadas. Ao longo dos anos, os cientistas tentaram
estabelecer sistemas de unidades universais como, por exemplo, o CGS, MKS e o SI.
1.2.1 Sistema Internacional (SI)
É derivado do MKS e foi adotado internacionalmente a partir dos anos 60. É o
padrão utilizado no mundo, mesmo que alguns pa´ıses ainda adotem algumas unidades
dos sistemas precedentes.
1.3 No¸cões de Padrão, Aferi¸cão e Calibra¸cão
1.3.1 Padrão
Padrão é um elemento ou instrumento de medida destinado a definir, conservar e
reproduzir a unidade base de medida de uma determinada grandeza. Possui uma alta
estabilidade com o tempo e é mantido em um ambiente neutro e controlado (temperatura,
pressão, umidade, etc. constantes).
Padrões de Grandezas Elétricas
Corrente Elétrica: O ampére é a corrente constante que, mantida entre dois condutores
paralelos de comprimento infinito e se¸cão transversal desprez´ıvel separados de 1m,
no vácuo, produz uma for¸ca entre os dois condutores de 2 · 10−7
N/m. Na prática
são utilizados instrumentos chamados “balan¸cas de corrente”, que medem a for¸ca
de atra¸cão entre duas bobinas idênticas e de eixos coincidentes.
Tensão: O padrão do volt é baseado numa pilha eletroqu´ımica conhecida como “Célula
Padrão de Weston”, constitu´ıda por cristais de sulfato de cádmio (CdSO4) e uma
pasta de sulfato de mercúrio (HgSO4) imersos em uma solu¸cão saturada de sulfato
de cádmio. Em uma concentra¸cão espec´ıfica da solu¸cão e temperatura de 20o
C a
tensão medida é de 1, 01830V .

Resistência: O padrão do ohm é normalmente baseado num fio de manganina (84% Cu,
12% Mn e 4% Ni) enrolado sob a forma de bobina e imerso num banho de óleo a
temperatura constante. A resistência depende do comprimento e do diâmetro do
fio, possuindo valores nominais entre 10−4
Ω e 106
Ω.
Capacitância: O padrão do farad é baseado no cálculo de capacitores de geometria
precisa e bem definida com um dielétrico de propriedades estáveis e bem conhecidas.
Normalmente usam-se duas esferas ou 2 cilindros concêntricos separados por um
dielétrico gasoso.
Indutância: O padrão do henri é também baseado no cálculo de indutores sob a forma
de bobinas cil´ındricas e longas em rela¸cão ao diâmetro com uma única camada de
espiras.
1.3.2 Aferi¸cão
Aferi¸cão é o procedimento de compara¸cão entre o valor lido por um instrumento e o
valor padrão apropriado de mesma natureza. Apresenta caráter passivo, pois os erros são
determinados, mas não corrigidos.
1.3.3 Calibra¸cão
Calibra¸cão é o procedimento que consiste em ajustar o valor lido por um instrumento
com o valor de mesma natureza. Apresenta caráter ativo, pois o erro, além de determi-
nado, é corrigido.
1.4 Classifica¸cão dos Erros
De acordo com a causa, ou origem, dos erros cometidos nas medidas, estes podem
ser classificados em: grosseiros, sistemáticos e acidentais. E de acordo com suas carac-
ter´ısticas, estes podem ser classificados em: constantes, aleatórios e periódicos.
1.4.1 Erros Grosseiros
Estes erros são causados por falha do operador, como por exemplo, a troca da posi¸cão
dos algarismos ao escrever os resultados, os enganos nas opera¸cões elementares efetuadas,
ou o posicionamento incorreto da v´ırgula nos números contendo decimais.
Estes erros podem ser evitados com a repeti¸cão dos ensaios pelo mesmo operador, ou
por outros operadores.
1.4.2 Erros Sistemáticos
São os ligados às deficiências do método utilizado, do material empregado e da apre-
cia¸cão do experimentador.
a. A constru¸cão e aferi¸cão de um aparelho de medida nunca podem ser perfeitas. Por
outro lado, há sempre uma divergência, embora pequena, entre a análise teórica de

um circuito e o comportamento prático deste circuito. As hipóteses de base da teoria
não são inteiramente realizáveis na prática. Basta mencionar, como exemplo, o
consumo de energia dos aparelhos de medida e as varia¸cões das caracter´ısticas f´ısicas
ou elétricas dos elementos que constituem o circuito. Este conjunto de imperfei¸cões
constitui a deficiência do método.
b. A própria defini¸cão dos erros sistemáticos indica quais são os meios de limita¸cão. O
material empregado deve ser aferido: medidores, pilhas, resistências, capacitores,
etc. O seu controle deve ser periódico. Um modo simples de verificar a presen¸ca
ou ausência de erro sistemático consiste na repeti¸cão da mesma experiência, substi-
tuindo os elementos iniciais por elementos teoricamente iguais. A identifica¸cão dos
resultados dá como conclusão a ausência do erro sistemático; porém, a discordância
indidca que há um erro, no método ou no material, sem identificar qual dos dois é
o responsável.
c. Há experimentadores que têm a peculiaridade de fazer a leitura maior do que a real,
enquanto outros a fazem menor. Este erro pode ser limitado tomando-se como
resultado a média aritmética das leituras de várias pessoas.
1.4.3 Erros Acidentais
A experiência mostra que, a mesma pessoa, realizando os mesmos ensaios com os
mesmos elementos constitutivos de um circuito elétrico, não consegue obter, cada vez, o
mesmo resultado. A divergência entre estes resultados é devida à existência de um fator
incontrolável, o “fator sorte”. Para usar uma terminologia mais cient´ıfica, diremos que
os erros acidentais são a conseqüência do “imponderável”. Como já foi dito, são erros
essencialmente variáveis e não suscet´ıveis de limita¸cão.
1.4.4 Erros Constantes
Erros invariáveis em aplitude e polaridade devido a imprecisões instrumentais. Em
geral, podem ser facilmente corrigidos pela compara¸cão com um padrão conhecido da
medida.
1.4.5 Erros Periódicos
Erros variáveis em amplitude e polaridade, mas que obedecem a uma certa lei (por
exemplo, a não linearidade de um conversor A/D). Podem ser eliminados pela medi¸cão
repetitiva sob condi¸cões distintas e conhecidas.
1.4.6 Erros Aleatórios
Erros Aleatórios são todos os erros restantes, possuem amplitude e polaridade variáveis
e não seguem necessariamente uma lei sistemática. São em geral pequenos, mas não estão
presentes em qualquer medida, provenientes de sinais espúrios, condi¸cões variáveis de
observa¸cão, ru´ıdos do próprio instrumento.

Erros Aleatórios: caracter´ısticas e limita¸cões
- os valores lidos possuem uma distribui¸cão estat´ıstica;
- cada medida é independente das outras;
- erros pequenos ocorrem com maior probabilidade que os grandes;
- erros importantes são aperiódicos;
- erros (+) e (−) possuem mesma amplitude e probabilidade de ocorrência e freqüência.
1.5 Erros Absoluto e Relativo
A palavra “erro”designa a diferen¸ca algébrica entre o valor medido Vm de uma grandeza
e o seu valor verdadeiro, ou aceito como verdadeiro, Ve:
∆V = Vm − Ve
Assim, o valor verdadeiro Ve da grandeza pode ser expresso da seguinte maneira:
Vm − ∆V ≤ Ve ≤ Vm + ∆V
O valor ∆V é chamado limite superior do erro absoluto, limite máximo do erro absoluto
ou simplesmente “erro absoluto”.
Quando o valor Vm encontrado na medida é maior que o valor verdadeiro Ve, diz-se que
o erro cometido é “por excesso”. Quando Vm é menor que Ve, diz-se que o erro cometido
é “por falta”.
O “erro relativo”ε é difinido como a rela¸cão entre o erro absoluto ∆V e o valor verda-
deiro Ve da grandeza medida:
ε = ∆V
Ve
Para efeito de cálculo de ε pode-se, na maioria dos casos, considerar Ve = Vm tendo-se
em conta que estes valores são muito aproximadamente iguais entre si.
O erro relativo percentual tem a forma:
ε = ∆V
Ve
· 100
1.6 Tratamento de erros em medidas
Com o intuito de minimizar e identificar os vários tipos de erros presentes numa
medida, um tratamento estat´ıstico pode ser aplicado num conjunto de dados obtidos em
condi¸cões idênticas e/ou conhecidas. Este tratamento estat´ıstico baseado na observa¸cão
repetitiva é eficaz na minimiza¸cão de erros periódicos e aleatórios.

1.6.1 Média Aritmética
A média aritmética ¯x é dada a partir da equa¸cão a seguir.
¯x =
n
i=1
xi
n
onde xi são os valores medidos e n é o número de medidas. O res´ıduo r é a diferen¸ca ente
a média e cada uma das medidas r = (¯x − xi).
1.6.2 Erro Padrão ou Desvio Padrão
O erro padrão σ é encontrado a partir de uma série de leituras e fornece uma estima-
tiva da amplitude do erro presente nestas medidas e consequentemente sua precisão. A
determina¸cão precisa do erro padrão σ implica num grande número de leituras.
σ =
r2
n − 1
sendo: r2
= (¯x − x1)2
+ (¯x − x2)2
+ . . . + (¯x − xi)2
Distibui¸cão Normal ou Curva Gaussiana
y = 1√
2πσ2
· e− r2
2σ2
onde σ2
é a variância, tp é o ponto de retorno (dy
dx
= 0) e pi são os pontos de inflexão
(d2y
d2x
= 0).
A área hachurada na curva representa 68, 3% da área total que equivale ao conjunto
de todas as medidas. O erro padrão σ de uma série de medidas indica então uma proba-
bilidade de 68, 3% que o valor verdadeiro da medida esteja entre −σ e +σ do valor médio
¯x do conjunto de dados. Consequentemente 2σ ⇒ 95, 4% e 3σ ⇒ 99, 7%.

1.6.3 Erro Limite
O erro limite L é uma forma de indica¸cão da margem de erro baseada nos valores
extremos (máximo e m´ınimo) poss´ıveis. Em geral, é definido como uma porcentagem do
valor padrão ou fundo de escala. Supõe uma probabilidade teórica de 100% de que o valor
verdadeiro (yv) esteja no intervalo y ± L.
Apesar de menos rigorosa, esta medida de erro é mais popular que o erro padrão,
pois indica o erro de forma mais direta e facilmente compreens´ıvel por um leigo. Numa
avalia¸cão rigorosa de dados, sempre que poss´ıvel deve-se usar a defini¸cão de erro padrão.
Exemplo:
a. R = 10kΩ ± 5%;
b. C = 10µF + 20% − 10%;
c. Em um instrumento: “precisão”= 5% (o termo “precisão”utilizado aqui deve ser
substitu´ıdo por “erro”).
1.6.4 Determina¸cão do valor mais provável
O valor verdadeiro xv da grandeza a ser medida é, em geral, desconhecido. Através
da teoria de erros pode-se determinar, com alto grau de exatidão, o valor mais provável
xp e o quanto este valor ifere do valor verdadeiro.
Num conjunto de medidas onde os erros predominantes são aleatórios, o valor mais
provável corresponde à média aritmética xp ≡ ¯x.
1.6.5 Intervalo de Confian¸ca
Faixa de valores compreendida entre xp ± σ (ou 2σ, 3σ, . . . ) ou xp ± L. Considerando
um conjunto de medidas quaisquer, a probabilidade de que o valor verdadeiro xv esteja
presente em xp ± σ é de 31, 7%.
1.7 Dados Caracter´ısticos dos Instrumentos Elétricos
de Medi¸cão
São indicados a seguir alguns dados caracter´ısticos essenciais dos instrumentos elétricos
de medi¸cão, dados estes importantes na utiliza¸cão correta dos mesmos.
1.7.1 Natureza do Instrumento
Natureza do instrumento é a caracter´ıstica que o identifica de acordo com o tipo
de grandeza mensurável pelo mesmo. Exemplo: amper´ımetro, volt´ımetro, watt´ımetro,
fas´ımetro, etc.

1.7.2 Natureza do Conjugado Motor
A natureza do conjugado motor caracteriza o princ´ıpio f´ısico de funcionamento do
instrumento; caracteriza o efeito da corrente elétrica aproveitado no mesmo. Exemplo:
eletrodinâmico - efeito de corrente elétrica sobre corrente elétrica; ferro-móvel - efeito do
campo magnético da corrente elétrica sobre pe¸ca de material ferromagnético; térmico -
efeito do aquecimento produzido pela corrente elétrica ao percorrer um condutor, etc.
1.7.3 Calibre do Instrumento
O calibre do instrumento é o valor máximo, da grandeza mensurável, que o isntrumento
é capaz de medir. Exemplo: um volt´ımetro que pode medir no máximo 200 volts, diz-se
que o seu calibre é de 200 volts. Há a considerar dois casos:
Instrumento de um só calibre: o valor do calibre corresponde, normalmente, ao valor
marcado no fim de sua escala. Exemplo: a figura abaixo representa um volt´ımetro
de calibre único, 200 volts.
Instrumento de múltiplo calibre: os valores dos respectivos calibres vêm indicados nas
várias posi¸cões da chave de comuta¸cão dos calibres, posi¸cões da chave de comuta;cão
dos calibres, podendo haver no mostrador apenas uma escala graduada. O valor de
uma grandeza medida num dos calibres será obtido pela rela¸cão:
Valor da grandeza = Calibre utilizado
Valor marcado no fim da escala
· Leitura
Exemplo: A figura abaixo representa um multivolt´ımetro cujos terminais 1 e 2 são
para liga¸cão do mesmo ao circuito elétrico cuja tensão se deseja medir, sendo a sua
escala graduada em divisões, de 0 a 200 divisões. Utilizando-se a chave de comuta¸cão
K no calibre de 300V , liga-se o volt´ımetro a um circuito elétrico obtendo-se a leitura
de 148 divisões. Portanto, o valor medido V da tensão será:
V = 300
200
· 148 = 222V
1.7.4 Discrepância
Discrepância é a diferen¸ca entre valores medidos para a mesma grandeza. Exemplo:
um volt´ımetro é empregado para medir a tensão de uma fonte, dando como primeira
leitura 218V e como segunda leitura 220V . Diz-se então que entre as duas medi¸cões há
uma discrepância de 2V .

1.7.5 Sensibilidade
Sensibilidade é a caracter´ıstica de um instrumento de medi¸cão que exprime a rela¸cão
entre o valor da grandeza medida e o deslocamento da indica¸cão. Exemplo: dois am-
per´ımetros são postos em série para medir uma mesma corrente I. No primeiro, observa-
se uma indica¸cão de x divisões na escala e no segundo, uma indica¸cão de 2x divisões.
Diz-se, então, que a sensibilidade do segundo amper´ımetro é o dobro da sensibilidade do
primeiro.
1.7.6 Resolu¸cão
Resolu¸cão é o menor incremento que se pode assegurar na leitura de um instrumento,
o que corresponde à menor divisão marcada na escala do instrumento.
1.7.7 Mobilidade
Mobilidade é a menor varia¸cão da grandeza medida capaz de usar um deslocamento
percept´ıvel no ponteiro ou na imagem luminosa.
1.7.8 Perda Própria
Perda própria é a potência consumida pelo instrumento correspondente à indica¸cão
final da escala, correspondente ao calibre. Exemplo: um amper´ımetro de calibre 10A e
resistência própria 0, 2Ω tem uma perda própria de 20W. É desejável que os instrumentos
elétricos de medi¸cão tenham a m´ınima perda própria a fim de que não perturbem o circuito
em que está ligado, sobretudo este circuito trata-se de um circuito de pequena potência.
Os instrumentos eletrônicos de medi¸cão são considerados de perda própria praticamente
nula.
1.7.9 Eficiência
Eficiência de um instrumento é a rela¸cão entre o seu calibre e a perda própria. Exem-
plo: levando em considera¸cão o exemplo do item anterior, a eficiência do amper´ımetro
seria: 10A/20W = 0, 5A/W. No caso de volt´ımetro é usual exprimir a eficiência em Ω/V ,
pois: V/W = RI/V I = R/V . Dois volt´ımetros, um de 800Ω/V e outro de 5000Ω/V , o
segundo tem melhor eficiência que o primeiro.
1.7.10 Rigidez Dielétrica
Rigidez dielétrica caracteriza a isola¸cão entre a parte ativa e a carca¸ca do instrumento.
A rigidez dielétrica é expressa por um certo número de quilovolts, chamado de “tensão
de prova”ou “tensão de ensaio”, o qual representa a tensão máxima que se pode aplicar
entre a parte ativa e a carca¸ca do instrumento sem que lhe cause danos.
Estes valores são representados nos instrumentos simbolicamente por uma estrela con-
tendo, ou não, um número em seu interior.

1.7.11 Categoria de Medi¸cão
Definido pelos padrões internacionais, a categoria de medi¸cão define categorias de
I a IV, onde os sistemas são divididos de acordo com a distribui¸cão de energia. Esta
divisão é baseada no fato de que um transiente perigoso de alta energia, como um raio,
será atenuado ou amortecido à medida que passa pela impedância (resistência CA) do
sistema.
1.7.12 Exatidão
Exatidão é a caracter´ıstica de um instrumento de medi¸cão que exprime o afastamento
entre a medida nele efetuada e o valor de referência aceito como verdadeiro. O valor da
exatidão de um instrumento de medi¸cão ou de um acessório é definido pelos limites do
erro intr´ınseco e pelos limites da varia¸cão na indica¸cão.
Como se vê, a exatidão de um instrumento é considerada em rela¸cão a um padrão, a um
valor aceito como verdadeiro. Pode-se dizer que a exatidão está diretamente relacionada
com as caracter´ısticas próprias do instrumento, a forma como foi projetado e constru´ıdo.
Os erros sistemáticos é que definem se um instrumento é mais exato ou menos exato que
outro. A exatidão vem indicada nos instrumentos elétricos de medi¸cão e nos acessórios
através da sua “classe de exatidão”.

Classe de Exatidão do Instrumento
A classe de exatidão do instrumento representa o limite de erro, garantido pelo fa-
bricante do instrumento, que se pode cometer em qualquer medida efetuada com este
instrumento. A classe de exatidão é representada pelo “´ındice de classe”, um número
abstrato, o qual deve ser tomado como uma percentagem do calibre do instrumento.
Exemplo: seja um volt´ımetro de calibre C = 300V e classe de exatidão 1, 5; o limite de
erro que se pode cometer em qualquer medida feita com este volt´ımetro é de 1, 5% de
300V , ou seja:
∆C = 300·1,5
100
= 4, 5V
Vê-se que o erro relativo percentual é ∆C
X
· 100 > 1, 5% para uma medi¸cão efetuada
de X volts. Isto mostra que o instrumento deve ser utilizado para medir grandezas de
valor o mais próximo poss´ıvel do ser calibre, onde teremos o erro relativo m´ınimo. Uma
prática usual é selecionar um instrumento de calibre tal que o calor medido se situe no
último ter¸co da escala.
Um instrumento elétrico de medi¸cão, quanto melhor é a sua classe de exatidão, mais
caro ele custa e mais cuidados ele requer na sua utiliza¸cão, com pessoal mais especializado.
Tendo em vista este fato é que os instrumentos elétricos de medi¸cão podem ser classificados
em dois grupos:
Instrumentos de Laboratório: são medidas realizadas em ambientes e condi¸cões ideais,
distintos do ambiente industrial. São medidas feitas para averiguar o funcionamento
dos dispositivos de medidas industriais, ou para o projeto de dispositivos e circuitos.
Devem ter uma maior precisão e por isso são mais caros e delicados. Classe de
exatidão de 0, 1 a 1, 5;
Instrumentos de Servi¸co, Instrumentos Industriais: são aquelas medidas feitas direta-
mente sobre a montagem industrial ou instala¸cão elétrica. São utilizados equipa-
mentos práticos tanto fixos como portáteis, classe de exatidão de 2 a 3, ou maior.
1.7.13 Repetibilidade (Precisão)
No Vocabulário Internacional de Metrologia, o termo Precisão foi substitu´ıdo por
Repetibilidade. Neste texto adotaremos o termo Repetibilidade.
Repetibilidade é a caracter´ıstica de um instrumento de medi¸cão, determinada através
de um processo estat´ıstico de medi¸cões, que exprime o afastamento mútuo entre as diversas
medidas obtidas de uma grandeza dada, em rela¸cão à média aritmética dessas medidas.
Ou seja, repetibilidade é a propriedade de um instrumento de, em condi¸cões idênticas,
indicar o mesmo valor para uma determinada grandeza medida.
Um instrumento preciso não é necessariamente exato, embora seja na maioria dos
casos. A repetibilidade está mais ligada à opera¸cão, ao fato de medir a grandeza. Ou
seja, é o termo que está necessariamente ligado a uma avalia¸cão estat´ıstica sobre os valores
resultantes de uma medida. A precisão exprime o grau de consistência ou reprodu¸cão nas
indica¸cões de uma medida sob as mesmas condi¸cões. A repetibilidade não vem indicada
nos intrumentos, pois ela resulta de uma análise estat´ıstica.
A repetibilidade de uma medida se faz através do “´ındice de repetibilidade”, comu-
mente dado em fun¸cão do desvio padrão sobre a média dos valores medidos. Assim,

quando se diz que determinado resultado tem uma repetibilidade de 0, 5% isto que dizer
que a rela¸cão σ/¯x ≤ 0, 005, onde σ é o desvio padrão.
A repetibilidade é um pré-requisito da exatidão, mas a repetibilidade não garante a
exatidão. As medidas efetuadas poderão ser tão mais precisas quanto mais exato for o
instrumento empregado.
Exemplo: Suponhamos um volt´ımetro, constru´ıdo com certa classe de exatidão, tem
sua resistência original substitu´ıda por outra de maior valor. Este volt´ımetro continua a
fazer medidas com a mesma repetibilidade, entretanto a sua exatidão pode estar muito
diferente daquela que ele tinha quando estava com a resistência original. A exatidão das
medidas somente pode ser comprovada através da compara¸cão do instrumento com um
padrão.
Exemplo: Suponhamos dois volt´ımetros de mesmo calibre, um de classe de exatidão
2 e outro de classe de exatidão 1. Os dois volt´ımetros poderão fazer medidas com a
mesma repetibilidade, porém o segundo indicará valores mais exatos, pois estes estarão
mais próximos do valor aceito como verdadeiro.
1.8 Princ´ıpios de Funcionamento de Instrumentos Ele-
tromecânicos
Os primeiros instrumentos utilizados para medidas de grandezas elétricas eram ba-
seados na deflexão de um ponteiro acoplado a uma bobina móvel imersa em um campo
magnético. Uma corrente aplicada na bobina produz o seu deslocamento pela for¸ca de Lo-
rentz. Um mecanismo de contra-rea¸cão (em geral uma mola) produz uma for¸ca contrária
de modo que a deflexão do ponteiro seja proporcional à corrente na bobina.
Estes instrumentos analógicos estão em desuso em fun¸cão de suas qualidades inferiores
se comparadas às dos instrumentos digitais (imprecisões de leitura, fragilidade, desgaste
mecânico, dif´ıcil automa¸cão de leitura, etc.).
Os instrumentos digitais atuais são inteiramente eletrônicos, não possuindo partes
móveis (exceto seletores de escala e teclas). São mais robustos, precisos, estáveis e

duráveis. São baseados em conversores analógico/digital (A/D) e são facilmente adaptáveis
a uma leitura automatizada. Além disso, o custo dos instrumentos digitais é em geral
inferior (com exce¸cão dos osciloscópios).
Contudo, iremos estudar os princ´ıpios gerais sobre instrumentos eletromecânicos de
medi¸cão para entendermos melhor o avan¸co dos instrumentos digitais.
1.8.1 Generalidades sobre Instrumentos Elétricos de Medi¸cão
Os instrumentos elétricos empregados na medi¸cão das grandezas elétricas têm sempre
um conjunto que é deslocado aproveitando um dos efeitos da corrente elétrica: efeito
térmico, efeito magnético, efeito dinâmico, etc. Preso ao conjunto móvel está um ponteiro
que se desloca na frente de uma escala graduada em valores da grandeza a que se destina
o instrumento medir, como na figura abaixo.
A corrente elétrica cont´ınua ao percorrer a bobina fica na presen¸ca do campo magnético
do imã permanente. A intera¸cão entre a corrente e o campo magnético origina as for¸cas
aplicadas aos condutores da bobina, for¸cas estas que produzem um conjugado em rela¸cão
ao eixo de rota¸cão do sistema, fazendo girar a bobina em torno deste eixo. Este conjunto
assim originado é chamado de “conjugado motor”.
Ao mesmo tempo as molas, com uma extremidade presa ao eixo da bobina e a outra à
carca¸ca do instrumento, ficam sob tensão mecânica e se opõem ao movimento de rota¸cão
da bobina, originando um “conjugado antagonista”ou “conjugado restaurador”. Estas
molas, além da oposi¸cão ao deslocamento do conjunto móvel, fazem-no voltar à posi¸cão
inicial (posi¸cão de repouso) cessado o efeito do conjugado motor.
Para evitar as oscila¸cões do conjunto móvel em torno da posi¸cão de equil´ıbrio, cria-
se um “conjugado de amortecimento”por meio de artif´ıcios externos ao sistema. Este
“conjugado de amortecimento”evita também os deslocamentos bruscos do conjunto móvel
ao partir da posi¸cão de repouso, como ao voltar a ela cessado o efeito do conjugado motor.
O conjunto móvel dos instrumentos elétricos é assim submetido a três conjugados:
1. O motor produzido pela grandeza a medir, aproveitando um dos efeitos da corrente
elétrica;

2. O antagonista produzido pelas molas;
3. O de amortecimento produzido por arranjos externos ao conjunto móvel.
1.8.2 Amortecimento do Movimento do Conjunto Móvel
Há três tipos principais de amortecimentos aplicados aos instrumentos elétricos de
medi¸cão: amortecimento por correntes de Foucault, por atrito sobre o ar e por atrito
sobre l´ıquido.
Amortecimento por Correntes de Foucault
A figura acima mostra o princ´ıpio f´ısico em que se baseia este amortecimento. O
disco de alum´ınio é rigidamente solidário ao eixo do conjunto móvel. Quando este se
desloca, movido pelo conjugado motor, o disco corta as linhas de fluxo do entreferro do
imã permanente. No disco são então induzidas correntes de Foucault. Como elas estão na
presen¸ca do campo magnético do mesmo imã permanente, a intera¸cão entre estas correntes
e o referido campo magnético dará origem a uma for¸ca cujo sentido se opõe ao movimento
do disco, produzindo assim um conjugado em rela¸cão ao eixo de rota¸cão, conjugado este
que é de amortecimento, pois a sua existência está condicionada ao movimento do disco.
O conjugado de amortecimento é diretamente proporcional à velocidade angular do disco.
Amortecimento por Atrito sobre o Ar
É provocado pela rea¸cão do ar sobre uma fina palheta metálica presa ao eixo de rota¸cão
do conjunto móvel, ao qual está também preso o ponteiro.
A figura abaixo mostra o artif´ıcio mais empregado para este tipo de amortecimento.
Pode ser demonstrado que o conjugado de amortecimento é proporcional à velocidade
angular do conjunto móvel.

Amortecimento por Atrito sobre L´ıquido
O l´ıquido mais usado é o óleo mineral, em virtude de suas caracter´ısticas, também
como isolante. A viscosidade do óleo é escolhida de acordo com o mais intenso ou menos
intenso amortecimento que se queira dar ao movimento do conjunto móvel. Demonstra-se
também em dinâmica dos l´ıquidos que o conjugado de amortecimento neste caso é ainda
proporcional à velocidade angular do conjunto móvel.
1.8.3 Suspensão do Conjunto Móvel
Esta é a parte mais delicada na constru¸cão dos instrumentos elétricos de medi¸cão,
devendo a suspensão do conjunto móvel ser feita com tal perfei¸cão a proporcionar um
movimento sem nenhum atrito. Há três tipos de suspensões mais empregadas: suspensão
por fio, por eixo (instrumento de “pivot”) e suspensão magnética.
Suspensão por Fio
Empregada, sobretudo, em instrumentos de alta sensibilidade, instrumentos de labo-
ratório.
O fio de suspensão mostrado na figura acima é, em geral, feito de uma liga fósforo-
bronze e tem três finalidades: suportar o conjunto móvel; fornecer, por intermédio da
tor¸cão, o conjugado antagonista; e servir como condutor para levar a corrente elétrica à
bobina.
A extremidade superior do fio é presa à carca¸ca do instrumento e a sua por¸cão inferior
é feita em forma de mola para permitir regular a tensão mecânica do fio e centralizar o
conjunto móvel.
Suspensão por Eixo
O eixo é feito de a¸co, tendo nas extremidades dois bicos pontudos de a¸co duro repou-
sando sobre dois apoios de rubi ou safira sintética.

O eixo pode ser vertical ou horizontal, como na figura acima. Devido a este detalhe,
deve-se ter o cuidado de utilizar o instrumento na posi¸cão correta indicada pelo fabricante,
no mostrador, por s´ımbolos que podem ser vistos na sessão a seguir.
Suspensão Magnética
É utilizada, sobretudo, nos instrumentos de eixo vertical. Dois pequenos imãs per-
manentes são empregados: um preso ao eixo do conjunto móvel e outro à carca¸ca do
instrumento.
A suspensão magnética pode ser de dois tipos: repulsão, conforme a figura acima, em
que pólos de mesmo nome são colocados em presen¸ca na parte inferior do eixo; e atra¸cão,
conforme figura acima, em que pólos de nomes contrários são colocados em presen¸ca na
parte superior do eixo.
O guia indicado nas figuras é feito de material não magnético e serve para evitar que
o conjunto móvel fuja da posi¸cão correta em que deve trabalhar.
Esta suspensão tem sido empregada com resultados satisfatórios nos medidores de
energia elétrica, eliminando consideravelmente o atrito no apoio inferior, uma vez que
com este artif´ıcio o conjunto móvel fica flutuando no ar. Isto fez com que a vida média
destes medidores aumentasse de 15 para 30 anos.
1.8.4 Processos de Leitura
Os instrumentos elétricos de medi¸cão, conforme o modo de indica¸cão do valor das
grandezas medidas, podem ser classificados em três tipos: indicadores, registradores e
acumuladores, ou totalizadores.
Instrumentos Indicadores
Sobre uma escala graduada, eles indicam o valor da grandeza a que se destinam medir.
Podem ser do tipo “ponteiro”para instrumentos analógicos de suspensão por eixo e do

tipo “feixe luminoso”ou “imagem luminosa”para instrumentos analógicos de suspensão
por fio.
Os instrumentos digitais podem utilizar leds, displays, ou monitores independente dos
tipos de instrumento; podendo inclusive, através de uma rede, possibilitar uma indica¸cão
remota .
Instrumentos Registradores
Em instrumentos analógicos, sobre um rolo de papel graduado, eles registram os valores
da grandeza a que se destinam medir. Depois, retirando-se o papel do instrumento, tem-
se uma idéia da varia¸cão da grandeza medida durante o per´ıodo de tempo em que este
instrumento esteve ligado.
Em instrumentos digitais, o registro é realizado através de memórias. O que facilita a
análise e o armazenamento de dados. Além de, através de uma rede, possibilitar a análise
de forma remota.
Acumuladores ou Totalizadores
O mostrador destes instrumentos indica o valor acumulado da grandeza medida, desde
o momento em que os mesmos foram instalados.
São especialmente destinados à medi¸cão de energia elétrica, levando em considera¸cão
a potência elétrica solicitada por uma carga e o tempo de utiliza¸cão da mesma. A quan-
tidade de energia elétrica solicitada durante um certo per´ıodo, um mês por exemplo, é
obtida pela diferen¸ca entre a leitura no fim do per´ıodo, chamada “leitura atual”, e a
leitura que foi feita no in´ıcio do per´ıodo, chamada “leitura anterior”.
1.9 Simbologia para Instrumentos de Medida
A utiliza¸cão correta dos instrumentos de medidas elétricas depende da escolha dos
instrumentos. Isto permite a medida correta das grandezas sem por em risco a vida
do operador e a integridade do equipamento. Para tanto, deve-se observar os s´ımbolos
gravados nos visores. As tabelas a seguir ilustram alguns dos s´ımbolos freqüentemente
utilizados em medidas elétricas e nos diagramas dos circuitos elétricos.

Para fixar a idéia, vamos dar um exemplo:
Significa¸cão: instrumento de ferro móvel, para correntes cont´ınua e alternada, classe
de exatidão 1, deve ser utilizado com o mostrador na posi¸cão horizontal, tensão de ensaio
2kV .
1.10 Precau¸cões na Utiliza¸cão
É aconselhável que o operador somente utilize um instrumento elétrico de medi¸cão se
tiver real certeza de que o está utilizando de modo correto. Esta precau¸cão faz evitar
acidentes para o operador e para o instrumento. Se o instrumento não é ainda conhecido
para o operador, antes de colocá-lo em opera¸cão, devem ser lidos os manuais de instru¸cões
fornecidos pelo fabricante.
Para fazer a medida de uma grandeza elétrica, é necessário selecionar o instrumento
adequado tendo em vista várias condi¸cões:
1. Natureza da grandeza que se quer medir: corrente, tensão, potência, energia, etc., e
o seu tipo, isto é, grandeza cont´ınua ou alternada.
2. Valor aproximado da grandeza para que se possa fazer a sele¸cão do calibre adequado.
Na prática, isto é quase sempre poss´ıvel em virtude dos dados caracter´ısticos do
equipamento fornecidos na sua placa de identifica¸cão. Por exemplo, deseja-se me-
dir a corrente solicitada por uma lâmpada de 200W, 220V , pode-se empregar um
amper´ımetro de calibre 1A, uma vez que, calculando a corrente solicitada por esta
lâmpada, se vê que ela é ligeiramente inferior a 1A.
Se não há condi¸cões para determinar previamente o valor aproximado da grandeza,
então deve ser selecionado um instrumento de calibre o maior poss´ıvel. Verificado
assim desta forma o valor da grandeza, pode-se então selecionar um calibre mais
adequado, de tal modo que o valor medido se situe no último ter¸co da escala do
instrumento utilizado, obtendo-se assim melhor resultado na medida.
3. O instrumento deve ter uma classe de exatidão compat´ıvel com a qualidade da gran-
deza que se está medindo e com a precisão que se deseja nos resultados que serão
obtidos.
4. Em rela¸cão à potência elétrica da fonte que alimenta o circuito em que vai ser intro-
duzido o instrumento de medi¸cão, este deve ser selecionado com uma eficiência a
melhor poss´ıvel a fim de que nenhuma influência cause no referido circuito.
5. É interessante analisar previamente a perturba¸cão que pode causar um determinado
instrumento de medi¸cão ao ser inserido num circuito. Este fato é ressaltado com
o exemplo seguinte: corriqueiramente é dito que todo amper´ımetro tem resistência
interna desprez´ıvel quando é utilizado para medir uma corrente elétrica. Esta afirma-
tiva é precipitada! É mais correto afirmar que a resistência interna do amper´ımetro

é pequena, mas não, desprez´ıvel. Poderá ser desprez´ıvel se realmente for muito me-
nor do que a resistência do circuito com a qual tenha sido posto em série. Para fixar
a idéia, suponhamos que uma fonte E = 10V alimenta uma resistência R = 1Ω,
conforme a figura abaixo.
Ora, a corrente I que circula através de R é de 10A. Se for introduzido em série
com R um amper´ımetro de resistência interna Ra = 1Ω, conforme a figura abaixo,
a corrente será agora I = 5A.
Isto mostra que o amper´ımetro causou uma perturba¸cão no circuito em virtude de
a sua resistência ser considerável, e não desprez´ıvel, diante do valor da resistência
R do circuito. Este exemplo é extensivo a todos os outros instrumentos elétricos de
medi¸cão e serve de alerta aos seus manipuladores.

Cap´ıtulo 2
Medi¸cão de Potências Ativa e
Reativa
2.1 Watt´ımetro Eletrodinâmico
A figura a seguir esquematiza este instrumento que consta essencialmente das seguintes
partes, além das molas restauradoras:
a. Uma bobina fixa Bc constitu´ıda de duas meias bobinas idênticas;
b. Uma bobina móvel Bp, à qual está preso o ponteiro, colocada entre as duas meias
bobinas Bc.
O movimento do conjunto móvel, bobina Bp, resulta da intera¸cão entre o campo
eletromagnético, criado pela corrente ic, e a corrente ip da bobina Bp. O seu funcionamento
é assim idêntico ao do instrumento de imã fixo e bobina móvel, sendo o imã permanente
substitu´ıdo por Bc, fazendo-se ressalva de que os eletrodinâmicos são utilizáveis tanto em
corrente cont´ınua como em corrente alternada.
A nota¸cão Bc e Bp é justificada pela utiliza¸cão destes instrumentos como watt´ımetro,
onde Bc é chamada bobina de corrente e Bp, bobina de potencial ou bobina de tensão. E
ainda, Lc é o coeficiente de auto-indu¸cão de Bc e Lp, de Bp.

Cap´ıtulo 2. Medi¸cão de Potências Ativa e Reativa 22
Consideremos uma carga Z submetida à tensão v e percorrida pela corrente i. Ligando
Bc em série com esta carga e Bp em paralelo, e considerando Rp >> ωLp, temos que ic = i
e ip = v
Rp
. O que nos dá a potência ativa da carga Z em watt, de modo que a leitura do
valor da potência ativa é feita diretamente.
2.1.1 Erro Sistemático do Watt´ımetro
Como mostram os dois esquemas seguintes é imposs´ıvel realizar, ao mesmo tempo, a
liga¸cão série Bc−carga e a liga¸cão paralela Bp−carga. A medi¸cão, portanto, comporta um
erro sistemático: seja com a influência da bobina Bc na corrente ic antes da medi¸cão de
Bp, ou na influência da corrente ip da bobina Bp fazendo que haja um desvio da corrente
total i = ic da carga e que é medida pela bobina Bc.
No caso em que se deseje um valor preciso de potência medida, é poss´ıvel determinar-se
o valor da potência perdida para subtra´ı-lo da indica¸cão do watt´ımetro.
2.1.2 Modo Prático de Ligar o Watt´ımetro
Antes de ligar um watt´ımetro, é preciso observar os valores máximos de corrente
e tensão suportáveis por Bc e Bp, respectivamente. Estes valores estão indicados no
mostrador do instrumento, como por exemplo, na figura abaixo em que Bc suporta no
máximo 5A e Bp, 300V .
Olhando para um watt´ımetro, facilmente identificamos os terminais das bobinas Bc e
Bp: os terminais de Bc têm maior se¸cão que os de Bp. Ou aqueles estão designados por
A1 e A2, e estes por V1 e V2.
Um terminal de Bc, como também um de Bp, está marcado com um sinal ± ou com
um aster´ıstico ∗. Isto indica a entrada das bobinas Bc e Bp.

Para que o watt´ımetro dê uma indica¸cão correta:
1. O terminal marcado de Bc deve ser ligado à fonte e o outro à carga, como mostra a
figura acima.
2. O terminal marcado de Bp deve ser ligado no condutor que está em série com Bc;
levando em conta o recomendado no item anterior, sua liga¸cão deve ser feita como
na figura acima, isto é, a bobina Bp ligada depois da bobina de corrente.
3. O terminal não marcado de Bp será ligado ao outro condutor, isto é, ligado ao ponto
B ou E ou D da figura acima.
4. O watt´ımetro pode dar indica¸cão para trás desde que o ângulo θ, entre a tensão
aplicada a Bp e a corrente que percorre Bc, tenha cos θ < 0. Para dar indica¸cão para
frente, é preciso inverter uma de suas duas bobinas Bc ou Bp, conforme mostram as
figuras abaixo.
Observamos que o watt´ımetro dá um desvio proporcional ao produto V I cos θ, onde:
V é o valor eficaz da tensão aplicada à Bp; I é o valor eficaz da corrente que percorre Bc;
e θ é o ângulo de defasagem entre V e I.
Como a escala do instrumento já é graduada em valores de potência, no caso em watts,
então a sua indica¸cão será:
W = V I · cos θ
Se as grandezas aplicadas ao watt´ımetro forem as mesmas aplicadas à carga, então
ele indicará a potência ativa da carga, conforme a expressão de W acima. Chamamos a
aten¸cão para este ponto porque pode acontecer de a carga ser alimentada com a tensão
V e percorrida pela corrente I, enquanto que o watt´ımetro tenha Bp submetida à tensão
U, diferente de V , e Bc percorrida pela mesma corrente I. A indica¸cão W do watt´ımetro
será neste caso:
W = UI · cos UI

2.2 Medi¸cão de Potência Elétrica em Corrente Alter-
nada
Para a medi¸cão da potência elétrica ativa solicitada por uma carga, empregamos o
watt´ımetro. O instrumento pode ser o mesmo, quer a fonte seja de corrente cont´ınua ou
de corrente alternada. Chamamos a aten¸cão para o fato de que a indica¸cão do watt´ımetro
é igual ao produto da tensão V aplicada à sua bobina de potencial Bp pela corrente I que
percorre a sua bobina de corrente Bc e pelo cosseno do ângulo de defasagem entre V e I:
W = V I · cos V I
Se V for a mesma tensão aplicada à carga e I a mesma corrente que percorre, então
a indica¸cão do watt´ımetro será a potência ativa absorvida pela carga.
Relembramos as expressões das potências elétricas em corrente alternada:
Potência Aparente: S = V I expressa em volt-ampére (V A).
Potência Ativa: P = V I · cos θ expressa em watt (W).
Potência Reativa: Q = V I · sin θ expressa em var (var).
É preciso também não esquecer a rela¸cão entre a tensão composta U (tensão entre
fases) e a tensão simples ¯V (tensão entre fase e neutro) nos circuitos trifásicos equilibrados:
U =
√
3 · V
Para os ciscuitos trifásicos equilibrados, as expressões das potências ficarão:
Potência Aparente: S = 3V I =
√
3 · UI.
Potência Ativa: P = 3V I · cos θ =
√
3 · UI cos θ.
Potência Reativa: Q = 3V I · sin θ =
√
3 · UI sin θ.
2.2.1 Métodos para Medi¸cão da Potência Ativa
Num circuito trifásico a potência instantânea é dada pela rela¸cão:
p = v1i1 + v2i2 + v3i3
onde: i1, i2 e i3 são as correntes das fases 1, 2 e 3, respectivamente; v1, v2 e v3 são as
respectivas tensões entre cada fase e o neutro.

Método dos Três Watt´ımetros: Circuitos de 3 Fases e um Neutro
Este método é aplicável para os circuitos trifásicos a quatro fios, equilibrados ou não,
sendo três fios de fase e um fio de neutro. Temos então:
P = V1I1 cos θ1 + V2I2 cos θ2 + V3I3 cos θ3
Aplicando então três watt´ımetros, como mostra a figura abaixo, temos que a soma das
suas indica¸cões respectivas representa a potência ativa total absorvida pela carga Z.
As indica¸cões dos watt´ımetros serão:
a. W = V1I1 cos V1I1
b. W = V2I2 cos V2I2
c. W = V3I3 cos V3I3
Levando em considera¸cão que a figura do diagrama fasorial corresponde ao esquema
da mesma figura, temos:
a. cos V1I1 = cos θ1
b. cos V2I2 = cos θ2
c. cos V3I3 = cos θ3
A indica¸cão total será: W = W1 + W2 + W3 e a potência ativa total: P = W. Se o
circuito é equilibrado, isto é, existem as igualdades:
a. V1 = V2 = V3 = V
b. I1 = I2 = I3 = I

c. θ1 = θ2 = θ3 = θ
então, teremos:
P = 3V I cos θ
Para este caso podemos empregar apenas um watt´ımetro e multiplicar a sua indica¸cão
por 3 para termos a potência ativa total P.
Método dos Dois Watt´ımetros: Circuitos de 3 Fases
Este método é aplicável para os circuitos trifásicos a três fios, equilibrados ou não,
sendo todos os três fios de fase. Poderá ser aplicado ao circuito de 4 fios se o mesmo for
equilibrado, o que significa não circular corrente no neutro.
Nos circuitos trifásicos a três fios, duas condi¸cões são sempre satisfeitas:
1. A soma das correntes de linha é sempre zero:
i1 + i2 + i3 = 0
Isto corresponde a:
I1 + I2 + I3 = 0
2. A soma das tensões compostas é sempre zero:
u12 + u23 + u31 = 0
Isto corresponde a:
U12 + U23 + U31 = 0
Explicitando i3 na expressão acima e substituindo na expressão de potência ins-
tantânea obtemos:
p = v1i1 + v2i2 − v3 (i1 + i2)
ou ainda:
p = (v1 − v3) i1 + (v2 − v3) i2
Podemos ainda escrever as seguintes rela¸cões:
v1 − v3 = u13 que é a tensão composta entre as fases 1 e 3
v2 − v3 = u23 que é a tensão composta entre as fases 2 e 3
Então:
p = u13i1 + u23i2
E a potência ativa total será:

P = U13I1 · cos U13, I1 + U23I2 · cos U23, I2
A figura acima indica a montagem a realizar com os dois watt´ımetros para a obten¸cão
de P. Cada watt´ımetro indicará:
a. W1 = U13I1 · cos U13, I1
b. W2 = U23I2 · cos U23, I2
Se o circuito é equilibrado, temos do diagrama fasorial da figura acima:
a. U13, I1 = 30o
− θ
b. U23, I2 = 30o
+ θ
Acarretando como conseqüência:
a. W1 = UI · cos (30o
− θ)
b. W2 = UI · cos (30o
+ θ)
Sobre as expressões acima faremos as seguintes observa¸cões:
1. θ < 60o
acarreta cos θ > 0, 5
Neste caso temos W1 e W2 positivos, isto é, os dois watt´ımetros dão indica¸cão para
a frente.
2. θ > 60o
acarreta cos θ < 0, 5
O primeiro watt´ımetro dá indica¸cão para frente, mas o segundo dá indica¸cão para
trás.
3. θ = 60o
acarreta cos θ = 0, 5
O primeiro watt´ımetro indica sozinho a potência ativa total da carga, pois o segundo
indica W2 = 0.

Os dois watt´ımetros sempre darão indica¸cões diferentes entre si. Somente para θ = 0
é que teremos: W1 = W2.
A potência ativa total P = W1+W2 é assim a soma algébrica das respectivas indica¸cões
dos dois watt´ımetros. Se acontecer o segundo caso num circuito, devemos inverter a bobina
de corrente Bc do segundo watt´ımetro de modo que o mesmo dê uma indica¸cão para frente
e este valor será subtra´ıdo da indica¸cão do primeiro instrumento para termos a potência
total P.
O fator de potência da carga pode ser calculado a partir das expressões:
cos θ = W1+W2√
3·UI
; sin θ = W1−W2
UI
; tgθ = W1+W2
W1−W2
·
√
3
Para este método, além da montagem da figura acima, pode ser realizadas as monta-
gens mostradas na figura abaixo, bastando para isto substituir na expressão da corrente
os valores correspondentes:
i1 = − (i2 + i3) ou i2 = − (i1 + i3)
2.2.2 Medi¸cão da Potência Reativa
A potência reativa solicitada por uma carga monofásica, de fator de potência cos θ, é
expressa como:
Q = V I · sin θ
Para a carga trifásica esta potência será:
Q = V1I1 sin θ1 + V2I2 sin θ2 + V3I3 sin θ3
Se a carga trifásica é equilibrada, esta expressão, ficará:
Q = 3V I · sin θ
Embora existam instrumentos especiais para medi¸cão de potência reativa, eles são
pouco empregados.Para os circuitos monofásicos emprega-se o watt´ımetro e mais um
volt´ımetro e um amper´ımetro, como mostra a figura abaixo.
Da´ı deduzimos: cos θ = P
V I
e consequentemente sin θ e ainda: Q = V I · sin θ. Para
os circuitos trifásicos empregamos o wattimetro tendo cuidado de alimentar a sua bobina
Bp com uma tensão defasada de 90o
em rela¸cão à tensão aplicada à carga.

Montagens para Medi¸cão da Potência Reativa em Circuitos Trifásicos
O circuito trifásico pode ser a 3 ou 4 fios, equilibrado ou não, a montagem a realizar
é a mostrada na figura abaixo. O fio neutro não é utilizado.
As indica¸cões dos watt´ımetros serão:
a. W1 = U23I1 cos U23I1
b. W2 = U31I2 cos U31I2
c. W3 = U12I3 cos U12I3
Do diagrama fasorial correspondente, mostrado na figura acima, temos:
a. cos U23I1 = cos (90o
− θ1) = sin θ1
b. cos U31I2 = cos (90o
− θ2) = sin θ2
c. cos U12I3 = cos (90o
− θ3) = sin θ3

Assim, a soma das indica¸cões será:
W = U23I1 sin θ1 + U31I2 sin θ2 + U12I3 sin θ3
Como as tensões são supostas sempre equilibradas temos que:
|U23| = |U31| = |U12| = U =
√
3 · V
Assim, a expressão toma a forma:
W =
√
3 · (V I1 sin θ1 + V I2 sin θ2 + V I3 sin θ3)
Comparando as equa¸cões, conclui-se que:
W =
√
3 · Q ∴ Q = W√
3
Ou seja: a potência reativa total Q da carga é igual à soma das indica¸cões dos três
watt´ımetros dividida por
√
3. Sendo o circuito trifásico equilibrado, podemos empregar
apenas o primeiro watt´ımetro como mostra a figura abaixo. Desta se conclui:
W1 = UI sin θ =
√
3 · V I sin θ
E neste caso para termos a potência reativa total Q:
Q =
√
3 · W1 ou seja: Q = 3V I sin θ
Costuma-se fazer a montagem da figura com três watt´ımetros na prática para verificar
se o circuito trifásico é realmente equilibrado, pois em caso afirmativo todos os watt´ımetros
darão a mesma indica¸cão:
W1 = W2 = W3
Ainda para os circuitos trifásicos equilibrados podemos empregar dois watt´ımetros
como na figura abaixo e teremos:
W = W1 + W2

Sequência das Fases
Na medi¸cão da potência ativa não importa a seqüência das fases. Mas, na medi¸cão da
potência reativa é muito importante conhecer a seqüência das fases, pois se a liga¸cão de
Bp não for a correta, como a indicada nas montagens anteriores, o instrumento pode dar
indica¸cão incorreta, inclusive em sentido contrário ao normal. A primeira vista parece que
é bastante inverter a liga¸cão de Bc e teremos a indica¸cão correta para a frente. Entretanto,
esta observa¸cão é feita para o fato da identifica¸cão da natureza da potência reativa, isto é,
indutiva ou capacitiva. Se a potência reativa for capacitiva, embora o instrumento esteja
com a liga¸cão correta, sua indica¸cão será para trás, como se pode ver na figura abaixo.
A indica¸cão do watt´ımetro:
W = U23I1 · cos U23, I1
Mas, do diagrama fasorial:
cos U23, I1 = cos (90o
+ θ) = − sin θ
Donde concluimos:
W = −U23I1 sin θ
Se a liga¸cão tivesse sido U32 ter´ıamos que a indica¸cão do watt´ımetro seria:
W = U32I1 sin θ
O módulo seria o mesmo, mas dir´ıamos que a potência reativa é indutiva, quando na
realidade é capacitiva.

Cap´ıtulo 3
Transformadores para Instrumentos
3.1 Introdu¸cão
Os transformadores para instrumentos são equipamentos elétricos projetados e cons-
tru´ıdos especificamente para alimentarem instrumentos elétricos de medi¸cão, controle ou
prote¸cão. São dois os tipos de transformadores para instrumentos.
Transformador de Potencial (TP)
É um transformador para instrumento cujo enrolamento primário é ligado em de-
riva¸cão com um circuito elétrico e cujo enrolamento secundário se destina a alimentar
bobinas de potencial de instrumentos elétricos de medi¸cão, controle ou prote¸cão. Na
prática é considerado um “redutor de tensão”, pois a tensão no seu circuito secundário é
normalmente menor que a tensão no seu enrolamento primário.
Transformador de Corrente (TC)
É um transformador para instrumento cujo enrolamento primário é ligado em série
em um circuito elétrico e cujo enrolamento secundário se destina a alimentar bobinas de
corrente de instrumentos elétricos de medi¸cão, controle ou prote¸cão. Na prática é consi-
derado um “redutor de corrente”, pois a corrente que percorre o seu circuito secundário
é normalmente menor que a corrente que percorre o seu enrolamento primário.
3.2 Generalidades sobre Transformadores
O transformador é um equipamento elétrico, estático, que recebe energia elétrica
e fornece energia elétrica. Um transformador consta essencialmente de dois circuitos
elétricos, acoplados através de um circuito magnético. Um dos circuitos elétricos, cha-
mado “primário”, recebe energia de uma fonte AC, e o outro, chamado “secundário”,
fornece energia da mesma forma e freqüência, mas usualmente sob tensão diferente, a
uma carga M.

Cap´ıtulo 3. Transformadores para Instrumentos 33
Os circuitos primário e secundário são bobinas de fios de cobre, em geral com n1 = n2
onde n1 é o número de espiras do primário e n2 é o número de espiras do secundário.
O circuito magnético, chamado “núcleo”, é de chapas de ferro-sil´ıcio justapostas, mas
isoladas umas das outras para reduzir as perdas por correntes de Foucault.
Admitindo que a potência fornecida ao primário é totalmente transferida ao secundário,
isto é, não há perdas, rendimento 100%, podemos escrever: U1I1 = U2I2 ou ainda:
U1
U2
= I2
I1
= n1
n2
Da expressão acima conclu´ımos: n1I1 = n2I2, o que significa ser o número de ampéres-
espiras do primário igual ao número de ampéres-espiras do secundário. Portanto:
I1 = n2
n1
· I2
Como I1 e I2 têm sentidos opostos, a rela¸cão fasorial entre elas será:
I1 = −n2
n1
· I2
E como E1 deve equilibrar a tensão aplicada U1, temos as sequintes rela¸cões fasoriais:
U2 = E2 e U1 = −E1
Agora, consideraremos um transformador real com todos os seus elementos considera-
dos: resistências dos enrolamentos primário r1 e secundário r2, corrente de excita¸cão I0,
fluxo de dispersão representados pelas “reatâncias de fuga”ou “reatâncias de dispersão”do
primário x1 e secundário x2.
Desta forma, a expressão do transformador ficará:
U1 = −E1 + r1I1 + jx1I1
U2 = E2 − r2I2 − jx2I2
onde a corrente do primário com a corrente de excita¸cão é I1 = −n2
n1
· I2 + I0.

3.3 Transformador de Potencial (TP)
A figura abaixo representa, esquematicamente, o transformador de potencial (TP). O
TP tem n1 > n2 dando assim uma tensão U2 < U1, sendo por isto considerado na prática
como um elemento “redutor de tensão”, pois uma tensão elevada U1 é transformada para
uma tensão reduzida U2 de valor suportável pelos instrumentos elétricos usuais.
Os TPs são projetados e constru´ıdos para uma tensão secundária nominal padronizada
em 115 volts, sendo a tensão primária nominal estabelecida de acordo com a tensão entre
fases do circuito em que o TP será ligado. Assim, são encontrados no mercado TPs para:
2300/115V , 13800/115V , 69000/115V , etc., isto significa que:
a. Quando no primário se aplica a tensão nominal para o qual o TP foi constru´ıdo, no
secundário tem-se 115 volts;
b. Quando no primário se aplica um tensão menor ou maior do que a nominal, no
secundário tem-se também uma tensão menor ou maior do que 115 volts, mas na
mesma propor¸cão das tensões nominais do TP utilizado. Exemplo: num TP de
13800/115V , ao aplicar-se a tensão de 13400V no primário, tem-se no secundário
112V ; ao aplicar-se a tensão de 14280V , tem-se no secundário 119V .
Os TPs a serem ligados entre fase e neutro são constru´ıdos para terem como tensão
primária nominal a tensão entre fases do circuito dividida por
√
3, e com tensão secundária
nominal 115/
√
3 volts ou 115V aproximadamente, podendo ainda ter estas duas possibi-
lidades de tensões ao mesmo tempo por meio de uma deriva¸cão conforme mostra a figura
abaixo.
Assim, são também encontrados no mercado TPs, por exemplo, para:

1. Tensão primária nominal: 13800/
√
3 volts
Tensão secundária nominal: 115/
√
3 volts, ou as duas tensões: 115/
√
3V e 115V
aproximadamente.
2. Tensão primária nominal: 69000/
√
3 volts
Tensão secundária nominal: 115/
√
3 volts, ou as duas tensões: 115/
√
3V e 115V
aproximadamente.
O quadro abaixo mostra as tensões primárias nominais e as rela¸cões nominais padro-
nizadas para os TPs fabricados normalmente no Brasil.
Os TPs são projetados e constru´ıdos para suportarem uma sobre-tensão de até 10%
em regime permanente, sem que nenhum dano lhes seja causado. Como os TPs são
empregados para alimentar instrumentos de alta impedância (volt´ımetros, bobinas de
potencial de watt´ımetros, bobinas de potencial de medidores de energia elétrica, relés
de tensão, etc.) a corrente secundária I2 é muito pequena e por isto se diz que são
transformadores de potência que funcionam quase em vazio.
3.3.1 Rela¸cão Nominal
U1n
U2n
= Kp

É a rela¸cão entre os valores nominais U1n e U2n das tensões primária e secundária,
respectivamente, tensões estas para as quais o TP foi projetado e constru´ıdo. A “rela¸cão
nominal”é a indicada pelo fabricante na placa de identifica¸cão do TP. É chamada também
de “rela¸cão de transforma¸cão nominal”, ou simplesmente de “rela¸cão de transforma¸cão”,
sendo nas aplica¸cões práticas considerada uma constante para cada TP. Ela é muito
aproximadamente igual à rela¸cão entre as espiras:
U1n
U2n
= Kp = n1
n2
3.3.2 Rela¸cão Real
U1
U2
= Kr
É a rela¸cão entre o valor exato U1 de uma tensão qualquer aplicada ao primário do
TP e o correspondente valor exato U2 verificado no secundário dele. Em virtude de o TP
ser um equipamento eletromagnético, a cada U1 corresponde um U2 e como conseqüência,
um Kr:
U1
U2
= Kr ;
U1
U2
= Kr ;
U1
U2
= Kr
Como também, para uma mesma tensão U1 aplicada ao primário, a cada carga colocada
no secundário do TP poderá corresponder um valor da tensão U2, e como conseqüência,
um Kr:
U1
U2
= Kr ; U1
U2
= Kr ; etc.
Estes valores de Kr são todos muito próximos entre si e também de Kp, pois os TPs são
projetados dentro de critérios especiais e são fabricados com materiais de boa qualidade
sob condi¸cões e cuidados também especiais.
Como não é poss´ıvel medir U2 e U1 com volt´ımetros (U1 tem normalmente valor ele-
vado), mede-se U2 e chega-se ao valor exato U1 através da constru¸cão do diagrama fasorial
do TP. Por isto é que a “rela¸cão real”aparece mais comumente indicada sob a forma se-
guinte:
U1
U2
= Kr
3.3.3 Fator de Corre¸cão de Rela¸cão
Kr
Kp
= FCRp
É o fator pelo qual deve ser multiplicada a “rela¸cão de transforma¸cão”Kp do TP para
se obter a sua rela¸cão real Kr.
De imediato vê-se que a cada Kr de um TP corresponderá um FCRp. Em virtude
destas varia¸cões, determinam-se os valores limites inferior e superior do FCRp para cada
TP, sob condi¸cões especificadas, partindo-se da´ı para o estabelecimento da sua “classe de
exatidão”, conforme será visto a seguir.

Na prática lemos o valor da tensão U2 com um volt´ımetro ligado ao secundário do TP
e multiplicamos este valor lido por Kp para obtermos o valor da tensão primária, valor
este que representa o “valor medido”desta tensão primária, e não o seu valor exato U1.
Exemplo: um TP de 13800/115V tem o primário ligado entre as duas fases de um
circuito de alta tensão e o secundário alimentando um volt´ımetro onde se lê: U2 = 113V .
Como a rela¸cão de transforma¸cão é neste caso Kp = 120, considera-se que a tensão do
circuito é:
KpU2 = 120 · 113 = 13560V
3.3.4 Diagrama Fasorial
O diagrama fasorial do TP, mostrado logo abaixo, é o mesmo do transformador geral.
A seguir é mostrado o racioc´ınio para sua constru¸cão.
Vamos tra¸car o diagrama fasorial do transformador considerando n1 > n2. No se-
cundário do transformador medem-se: U2, I2 e θ2, grandezas estas que dependem do tipo
de carga que o transformador alimenta. Escolhendo-se uma escala conveniente para repre-
senta¸cão gráfica dos fasores, fixa-se a posi¸cão do fasor I2 em rela¸cão ao fasor U2 e adota-se
a seguinte seqüência:
a. A partir da extremidade de U2, tra¸ca-se r2I2 paralelo a I2 por representar a queda de
tensão na resistência própria do enrolamento secundário.
b. A partir da extremidade de r2I2 tra¸ca-se x2I2 adiantado de 90o
em rela¸cão a I2 por
representar a queda de tensão na reatância de dispersão do secundário.
c. Unindo-se o ponto 0 à extremidade do fasor x2I2, determina-se o fasor E2 representa-
tivo da f.e.m. do enrolamento secundário.
d. O fasor E1 está em fase com E2, sendo o seu módulo determinado pela seguinte
rela¸cão: E1 = n1
n2
· E2
e. Adiantando-se de 90o
em rela¸cão a E1 e E2 tra¸ca-se o fasor representativo do fluxo φ.
f. A corrente de excita¸cão I0, a qual é cerca de 1% da corrente nominal primária,
e o ângulo θ0 são determinados por meio de um ensaio em vazio. No diagrama
fasorial I0 é posicionado em rela¸cão a −E1 uma vez que em vazio pode-se considerar:
U1 = −E1. Na figura, o fasor I0 não está em escala para possibilitar uma melhor
visualiza¸cão da figura.
g. A partir da extremidade de I0 tra¸ca-se um fasor paralelo a I2, porém de sentido
contrário, de módulo: n1
n2
· I2.
h. Unindo-se o ponto 0 à extremidade do fasor acima, determina-se o fasor I1.
i. A partir da extremidade de −E1 tra¸ca-se r1I1 paralelo a I1 por representar a queda
de tensão na resistência própria do enrolamento primário.
j. A partir da extremidade de r1I1 tra¸ca-se x1I1 adiantado de 90o
em rela¸cão à I1 por
representar a queda de tensão na reatância de dispersão do primário.

k. Unindo-se o ponto 0 à extremidade de x1I1 determina-se o fasor U1 representativo da
tensão aplicada ao enrolamento primário do transformador.
Se não houvesse a corrente I0, a corrente I1 estaria defasada de exatamente 180o
em
rela¸cão à corrente I2. Se o transformador fosse perfeito, isto é, sem perdas e sem fugas, a
tensão U1 estaria também defasada de 180o
em rela¸cão à tensão U2.
No exemplo citado anteriormente, o valor encontrado de 13560V é o valor medido da
tensão primária do TP. Para determinar o valor verdadeiro U1 desta tensão, ter-se-á de
construir o diagrama fasorial deste TP como aparece na figura acima. Assim, para fixar
a idéia:
a. KpU2 é o valor medido da tensão primária;
b. |U1| = U1 é o valor verdadeiro ou exato da tensão primária obtido no diagrama
fasorial, o qual pode diferir ligeiramente de KpU2.
Ainda na figura acima, pode ser visto que o inverso de U2 está defasado de um ângulo
γ em rela¸cão à U1. Num TP ideal este ângulo γ seria zero.
Estas considera¸cões levam a concluir que o TP, ao refletir no secundário o que se passa
no primário, pode introduzir dois tipos de erros.
3.3.5 Erros do TP
Erro de Rela¸cão εp
valor relativo: εp = KpU2−|U1|
|U1|
valor percentual: ε%
p = KpU2−|U1|
|U1|
· 100
Quando εp e FCRp estão expressos em valores percentuais, há o seguinte relaciona-
mento entre eles:

ε%
p = 100 − FCR%
p
Esta expressão mostra a equivalência correta entre o erro de rela¸cão εp e o fator de
corre¸cão de rela¸cão FCRp, cujos valores indicados no paralelogramo de exatidão estão
perfeitamente coerentes com esta equivalência.
Para fins de racioc´ınio, podem ser deduzidas as duas conclusões seguintes:
1. Kp < Kr acarreta FCRp > 100% e εp < 0:
Neste caso, o valor considerado KpU2 para a tensão primária (chamado de valor
medido) é menor do que o seu valor verdadeiro U1; há, portanto, um erro por falta;
2. Kp > Kr acarreta FCRp < 100% e εp > 0:
Neste caso, o valor considerado KpU2 para a tensão primária (chamado de valor
medido) é maior do que o seu valor verdadeiro U1; há, portanto, um erro por excesso;
Há uma preferência na prática em se trabalhar com o FCRp em lugar do εp, pois
aquele fator é simplesmente um número abstrato, independente de sinal, e dá a entender
exatamente o que se quer em rela¸cão à tensão primária refletida no secundário, isto é, se
há erro por falta ou por excesso no valor a ela atribu´ıdo.
Em termos práticos não é usual o levantamento do diagrama fasorial como método para
a determina¸cão dos erros de rela¸cão e de fase de um TP, em virtude dos inconvenientes e
dificuldades inerentes a este pretenso método.
Para se determinar estes erros, e consequentemente a classe de exatidão de um TP,
prefere-se na prática, por simplicidade, comparar o TP com um TP padrão idêntico a ele,
de mesma rela¸cão de transforma¸cão nominal, porém sem erros, ou de erros conhecidos.
Para fixar a idéia, vamos dar um exemplo numérico. Ao primário de um TP de
13800/115V , sob ensaio aplica-se uma certa tensão que faz surgir no secundário a tensão
de 114V , comprovada através de um volt´ımetro. Constata-se depois que a tensão primária
fora de exatamente 13800V . Determinar: Kp, Kr, FCRp e ε%
p .
Rela¸cão de Transforma¸cão Nominal: Kp = 13800/115 = 120
Rela¸cão Real: Kr = 13800/114 = 121, 053
Fator de Corre¸cão de Rela¸cão: FCRp = 121, 053/120 = 1, 00877 ou FCRp = 100, 877%
Erro de Rela¸cão: ε%
p = 100 − 100, 877 = −0, 877%
Sendo neste exemplo FCRp > 100% (εp < 0), conclu´ı-se que o erro cometido em
rela¸cão à tensão primária é por falta, pois a esta tensão seria atribu´ıdo o valor: U1 =
120 · 114 ∴ U1 = 13680V .
Erro de Fase ou Ângulo de Fase
É o ângulo de defasagem γ existente entre U1 e o inverso de U2. Se o inverso de U2 é
adiantado em rela¸cão a U1, γ é positivo. Em caso contrário, é negativo.

3.3.6 Classes de Exatidão dos TPs
Do diagrama fasorial conclui-se de imediato que para um mesmo TP, submetido à uma
tensão primária U1, os erros de rela¸cão e de fase variam com o tipo de carga utilizada no
seu secundário, isto é, eles são fun¸cão de I2 e θ2. É desejável na prática que estes erros
sejam os menores poss´ıveis.
Em virtude deste fato, e com o objetivo de detectar a qualidade dos TPs e o seu
comportamento provável nas instala¸cões, as normas técnicas estabelecem certas condi¸cões
sob as quais estes transformadores devem ser ensaiados, definindo a partir da´ı a “classe
de exatidão”dos mesmos.
Os TPs são enquadrados em uma ou mais das três seguintes classe de exatidão: classe
de exatidão 0, 3, 0, 6 e 1, 2. Considera-se que um TP está dentro de sua classe de exatidão
em condi¸cões especificadas quando, nestas condi¸cões, o ponto determinado pelo erro de
rela¸cão εp ou pelo fator de corre¸cão de rela¸cão FCRp e pelo ângulo de fase γ estiver dentro
do “paralelogramo de exatidão”especificado na figura abaixo correspondente à sua classe
de exatidão.
Para se estabelecer a classe de exatidão dos TPs estes são ensaiados em vazio e depois
com cargas padronizadas colocadas no seu secundário, uma de cada vez, sob as seguintes
condi¸cões de tensão: tensão nominal, 90% da tensão nominal e 110% da tensão nominal.
Estas tensões de ensaio cobrem a faixa de tensões prováveis das instala¸cões em que os
TPs serão utilizados.
As cargas padronizadas, acima referidas, estão relacionadas no quadro abaixo. É
interessante ressaltar que estas cargas não foram “criadas”aleatoriamente, mas sim tendo
em vista os tipos de instrumentos elétricos que são usualmente empregados no secundário
dos TPs, instrumentos aqueles com os quais tais cargas se assemelham em caracter´ısticas
elétricas.

Para melhor entendimento do paralelogramo de exatidão, suponhamos que um TP,
ensaiado com uma das cargas do quadro acima, apresentou:
erro de rela¸cão: εp = −0, 2% o que corresponde ao FCRp = 100, 2%
ângulo de fase: γ = 20
O ponto correspondente a estes valores fica for a dos paralelogramos representativos
das classes 0, 3 e 0, 6. Entretanto fica dentro do paralelogramo da classe 1, 2. Então este
TP será considerado de classe de exatidão 1, 2 para a carga de ensaio, embora o erro de
rela¸cão tenha sido de apenas 0, 2%.
Se na placa de um TP está indicado: 0, 3WXY ; 0, 6Z isto significa que:
1. o TP ensaiado com as cargas padronizadas W, X e Y tem classe de exatidão 0, 3, isto
é, apresenta erro de rela¸cão −0, 3% ≤ εp ≤ 0, 3% e ângulo de fase γ tal que o ponto
correspondente a estes erros fica dentro do paralelogramo de classe 0, 3%;
2. ensaiado com a carga padronizada Z tem classe de exatidão 0, 6.
Na designa¸cão da ABNT aquela indica¸cão na placa do TP seria representada por
0, 3 − P75; 0, 6 − P200 .
O quadro abaixo mostra como selecionar a exatidão adequada para um TP tendo em
vista a sua aplica¸cão nas diferentes categorias de medi¸cões.

3.3.7 Fator de Corre¸cão de Transforma¸cão (FCTp) do TP
É interessante observar que na medi¸cão de tensão, isto é, quando o TP está alimen-
tando apenas volt´ımetro, o FCRp é o único que tem efeito nos valores medidos. Mas,
quando o TP alimenta instrumento cuja indica¸cão depende dos respectivos módulos da
tensão e da corrente a ele aplicadas e também do ângulo de defasagem entre estas duas
grandezas, como no caso de watt´ımetros e medidos de energia elétrica, então o FCRp e o
ângulo de fase γ têm efeito simultâneo nos valores medidos, e por isto devem ser ambos
levados em considera¸cão na análise dos resultados.
Com isto chega-se ao “fator de corre¸cão de transforma¸cão”FCTp que é definido da
seguinte maneira: fator pelo qual se deve multiplicar a leitura indicada por um watt´ımetro,
ou por um medidor de energia elétrica, cuja bobina de potencial é alimentada através do
referido TP, para corrigir o efeito combinado do fator de corre¸cão de rela¸cão FCRp e do
ângulo de fase γ.
A montagem da figura abaixo esquematiza o que foi dito acima.
As normas técnicas definem o tra¸cado dos paralelogramos de exatidão baseando-se
no FCTp e na carga medida no primário do TP (carga M na figura acima), para o
qual estabelecem que o fator de potência deve ser indutivo e ter um valor compreendido
entre 0, 6 e 1. Fica então entendido que a exatidão do TP, indicada na sua placa de
identifica¸cão, somente é garantida para cargas medidas daquele tipo, isto é, com fator de
potência indutivo entre 0, 6 e 1.
Para qualquer fator de corre¸cão da rela¸cão (FCRp) conhecido de um TP, o valor limite
positivo ou negativo do ângulo de fase (γ) em minutos é expresso por:
γ = 2600 (FCTp − FCRp)
onde o fator de corre¸cão da transforma¸cão (FCTp) deste TP assume os seus valores
máximo e m´ınimo.
Justamente, a partir da expressão acima é que se constrói o paralelogramo de exatidão
correspondente a cada classe, pois, fixado um valor numérico para o FCTp, vê-se que esta
expressão representa a equa¸cão de uma reta. E de acordo com o que foi dito acima, o
FCTp pode ter dois valores em cada classe de exatidão:
a. 1, 003 e 0, 997 na classe de exatidão 0, 3
b. 1, 006 e 0, 994 na classe de exatidão 0, 6
c. 1, 012 e 0, 988 na classe de exatidão 1, 2

Para se tra¸car o paralelogramo referente a uma classe de exatidão, atribui-se ao FCTp
o seu valor máximo e faz-se variar o FCRp desde o seu limite superior até o limite inferior,
obtendo-se assim os valores positivos de γ, podendo-se então tra¸car um lado inclinado da
figura. Em seguida, atribui-se ao FCTp o seu valor m´ınimo e faz-se novamente o FCRp
variar, obtendo-se agora os valores negativos de γ e conseqüentemente o outro inclinado
da figura.
3.3.8 Como Especificar um TP
Para se especificar corretamente um TP, é necessário antes de tudo saber-se qual
será a finalidade da sua aplica¸cão, pois isto definirá a classe de exatidão, conforme visto
anteriormente.
A potência nominal do TP será estabelecida tendo em vista as caracter´ısticas (em
termos de perdas elétricas internas) dos instrumentos elétricos que serão inseridos no
secundário, caracter´ısticas estas que são normalmente fornecidas pelos seus fabricantes ou
poderão ser determinadas em laboratório através de ensaios apropriados. O quadro da
figura abaixo indica, a t´ıtulo de referência, a ordem de grandeza das perdas da bobina
de potencial de alguns instrumentos elétricos que são utilizados com TPs, em condi¸cões
de 115V , 60Hz. É poss´ıvel, partindo da´ı, chegar-se às caracter´ısticas Z, R e L de cada
bobina, caso se deseje. Convém aqui lembrar que para a bobina de potencial dos medidores
de energia elétrica, que as perdas não deverão exceder 2W e 8V A. Os ensaios devem ser
feitos em condi¸cões nominais.
Para fixar idéia na especifica¸cão de TPs, vamos dar dois exemplos.
Exemplo 1
Especificar um TP para medi¸cão de energia elétrica para faturamento a um consumidor
energizado em 69kV , em que serão utilizados os seguintes instrumentos:
a. Medidor de kWh com indicador de demanda máxima tipo mecânico.

b. Medidor de kvarh, espec´ıfico para energia reativa, sem indicador de demanda máxima.
Solu¸cão:
a. Classe de exatidão: o quadro de classe de exatidão indica 0, 3.
b. Potência do TP: os fabricantes dos instrumentos elétricos que serão utilizados forne-
ceram o seguinte quadro de perdas em 115V , 60Hz:
Da´ı, chega-se a:
S = (6, 0)2 + (19, 3)2 ∴ S = 20, 21V A
Com estes resultados e consultando o quadro da figura de cargas nominais, vê-se
que o TP deve ser de carga nominal pelo menos de 25V A que é a carga padronizada
para ensaio de exatidão imediatamente superior a 20, 21V A. A especifica¸cão deste
TP, do ponto de vista elétrico, pode então ter o seguinte enunciado: Transforma-
dor de potencial, tensão primária nominal 69000V , rela¸cão nominal 600 : 1, 60Hz,
carga nominal ABNT P25, classe de exatidão ABNT 0, 3−P25 (ou ANSI 0, 3WX),
potência térmica 1000V A, grupo de liga¸cão 1, para uso exterior (ou interior, con-
forme for o caso), n´ıvel de isolamento: tensão nominal 69kV , tensão máxima de
opera¸cão 72, 5kV , tensões suportáveis nominais à freqüência industrial e de impulso
atmosférico: 140kV e 350kV , respectivamente.
Exemplo 2
Especificar um TP para medi¸cão de energia elétrica e controle em 13, 8kV , sem fina-
lidade de faturamento, em que serão utilizados os seguintes instrumentos:
b. Medidor de kWh, sem indicador de demanda máxima, acoplado a um autotransfor-
mador de defasamento, servindo assim para medir kvarh.
c. Watt´ımetro.
d. Var´ımetro.
e. Volt´ımetro.
f. Fas´ımetro.
Solu¸cão:

a. Classe de exatidão: o quadro da classe de exatidão indica 0, 6 ou 1, 2 (a optar pelo
comprador).
b. Potência do TP: os fabricantes dos instrumentos elétricos que serão utilizados forne-
ceram o seguinte quadro de perdas:
Da´ı, chega-se a:
S = (21, 9)2 + (30, 4)2 ∴ S = 37, 46V A
Com estes resultados e consultando o quadro da figura de cargas nominais, vê-se que
o TP deve ser de carga nominal pelo menos de 75V A que é a carga padronizada para
ensaio de exatidão imediatamente superior a 37, 46V A. A especifica¸cão deste TP,
do ponto de vista elétrico, pode então ter o seguinte enunciado: Transformador de
potencial, tensão primária nominal 13800V , rela¸cão nominal 120 : 1, 60Hz, carga
nominal ABNT P75, classe de exatidão ABNT 0, 6 − P75 (ou ANSI 0, 6WXY ),
potência térmica 400V A, grupo de liga¸cão 1, para uso exterior (ou interior, conforme
for o caso), n´ıvel de isolamento: tensão nominal 13, 8kV , tensão máxima de opera¸cão
15kV , tensões suportáveis nominais à freqüência industrial e de impulso atmosférico:
36kV e 110kV , respectivamente.
Observa¸cões
1. Na constru¸cão dos TPs modernos, é normal conseguir-se a classe de exatidão ABNT
0, 3 − P200 (ou ANSI 0, 3WXY Z) sem alterar em muito o pre¸co do equipamento,
gra¸cas à evolu¸cão tecnológica dos tipos de materiais utilizados. Para que os TPs
citados nos exemplos 1 e 2 possam ser empregados em medi¸cão para fins de fatu-
ramento, e também em medi¸cão para fins de controle, eles devem ser especificados,
quanto à exatidão, pelo menos como: ABNT 0, 6−P75; 0, 6−P25 (ou ANSI 0, 3WX;
0, 6Y ).
2. No dimensionamento da carga nominal de um TP a ser empregado numa instala¸cão,
não há necessidade de se considerar a resistência elétrica dos condutores que ligam
os instrumentos elétricos ao TP. Como referência, podemos tomar os dois exemplos
citados anteriormente. Supondo que os instrumentos ficarão a 25m do TP e serão
ligados a este por meio de fio de cobre no
12AWG (resistência elétrica: 5, 3Ω/km),
ter´ıamos como perdas nos condutores:

No exemplo 1: 0, 0082W, o que é desprez´ıvel na frente da carga de 20, 21V A
imposta pelos instrumentos elétricos ao TP.
No exemplo 2: 0, 028W, o que é também desprez´ıvel na frente da carga de 37, 46V A
imposta pelos instrumentos elétricos ao TP.
3. Ressaltamos que os dois exemplos dados servem apenas como orienta¸cão de dimensi-
onamento. Para cada caso, devem considerados os valores corretos das perdas dos
instrumentos que serão utilizados na medi¸cão, e não ordem de grandeza dessas per-
das, pois há uma variedade considerável de instrumentos e, em conseqüência, uma
faixa muito larga de diferentes valores de perdas.
3.3.9 Transformador de Potencial Capacitivo (TPC)
Em circuitos de alta tensão e extra tensão, é mais conveniente e econômico o emprego
dos TPs tipo capacitivo em lugar dos TPs tipo indu¸cão, analisados até agora.
A Figura abaixo mostra o esquema elétrico básico destes TPCs, onde se vê que o
primário, constitu´ıdo por um conjunto C1 e C2 de elementos capacitivos em série, é ligado
entre fase e terra, havendo uma deriva¸cão intermediária B, correspondente a uma tensão U
da ordem de 5kV a 15kV , para alimentar o enrolamento primário de um TP tipo indu¸cão
intermediário, o qual fornecerá a tensão U2 aos instrumentos de medi¸cão e dispositivos de
prote¸cão ali inseridos.
Um reator, projetado e constru´ıdo pelo fabricante, é posto em série com o primário
do TP intermediário de modo que o conjunto tenha uma reatância Lω que satisfa¸ca a
seguinte igualdade:
Lω =
1
(C1 + C2) ω
A partir da Figura acima se pode estabelecer a rela¸cão entre as tensões primária e
secundária. Dela podemos deduzir as expressões de U1 e de U:
U1 = −
j (I + I1)
C1ω
−
jI
C2ω
U = −
jI
C2ω
− jLωI1

Levando em considera¸cão o valor de Lω, obtemos:
U = −
jI1
C2ω
−
jI1
(C1 + C2) ω
Dividindo membro a membro temos:
U1
U
=
C1 + C2
C1
A expressão acima mostra que a rela¸cão entre as tensões U1 e U independe da corrente.
Isto é verdade, pois em vazio, insto é, quando o TP intermediário não estiver ligado,
obtém-se o mesmo valor que o obtido na equa¸cão acima para a rela¸cão entre U1 e U.
Vejamos: 


U1 = −
j (I + I1)
C1ω
−
jI
C2ω
= −
jI
ω
C1 + C2
C1C2
U = −
jI
C2ω
Novamente, dividindo membro a membro, obtemos:
U1
U
=
C1 + C2
C1
Sendo o TP intermediário constru´ıdo de tal modo que: U = KU2, a expressão acima
toma forma:
U1
U2
= K ·
C1 + C2
C1
O TPC sendo constru´ıdo para as tensões U1 e U2 tais que representem os valores
nominais, então a expressão acima é o valor da rela¸cão de transforma¸cão nominal Kp do
TPC:
U1n
U2n
= Kp
Onde Kp equivale a:
Kp = K ·
C1 + C2
C1
Observa¸cões:
1. Os TPCs são constru´ıdos para tensões primárias de 34, 5kV a 765kV , sendo a tensão
intermediária de 5kV a 15kV e a tensão secundária de 115V e 115/
√
3V .
2. Os TPCs têm perdas bastante reduzidas e oferecem a possibilidade de acoplamento
para onda portadora de alta freqüência (telefonia). Sendo estas suas duas grandes
vantagens.
3. Apresentam, entretanto um grande inconveniente: a influência acentuada que podem
sofrer por motivo da varia¸cão da freqüência.
4. É aconselhável consultar a documenta¸cão fornecida juntamente aos TPCs pelos seus
fabricantes.

3.3.10 Resumo das Caracter´ısticas dos TPs
1. Tensão secundária: a tensão secundária nominal é 115V , ou aproximadamente 115V ,
havendo também a possibilidade de 115/
√
3V . Em TPs antigos podem ser encon-
tradas as tensões secundárias nominais: 110V , 120V , e às vezes 125V .
2. Tensão primária: a tensão primária nominal depende da tensão entre fases, ou entre
fase e neutro, do circuito em que o TP vai ser utilizado.
3. Classe de exatidão: valor máximo do erro, expresso em percentagem, que poderá ser
introduzido pelo TP na indica¸cão de um watt´ımetro, ou no registro de um medidor
de energia elétrica, em condi¸cões especificadas. Pode ter os valores: 0, 3, 0, 6 e 1, 2.
4. Carga nominal: carga na qual se baseiam os requisitos de exatidão do TP.
5. Potência térmica: maior potência aparente que um TP pode fornecer em regime
permanente, sob tensão e freqüência nominais, sem exceder os limites de eleva¸cão de
temperatura especificados. Estes limites de eleva¸cão de temperatura estão levando
em considera¸cão os diferentes tipos de materiais isolantes que podem ser utilizados
no TPs.
a. Para TPs pertencentes aos grupos de liga¸cão 1 e 2, a potência térmica nominal
não deve ser inferior a 1, 33 vezes a carga mais alta em volt-ampéres, referente
à exatidão do TP.
b. Para TPs pertencentes ao grupo de liga¸cão 3, a potência térmica nominal não
deve ser inferior a 3, 6 vezes a carga mais alta em volt-ampéres, referente à
exatidão do TP.
6. N´ıvel de isolamento: define a especifica¸cão do TP quanto às condi¸cões a que deve
satisfazer a sua isola¸cão em termos de tensão suportável. A padroniza¸cão das tensões
máximas de opera¸cão dos TPs (tabela abaixo), como também os correspondentes
tipos e n´ıveis de tensões a que devem ser submetidos por ocasião dos ensaios definem
desta maneira, a “tensão máxima de opera¸cão de um equipamento”: máxima tensão
de linha (tensão entre fases) para o qual o equipamento é projetado, considerando-
se principalmente a sua isola¸cão, bem como outras caracter´ısticas que podem ser
referidas a essa tensão, na especifica¸cão do equipamento considerado. Em caso de
corrente alternada é sempre dada em valor eficaz. Essa tensão não é necessariamente
igual à tensão máxima de opera¸cão do sistema ao qual o equipamento está ligado.
Tensões Máximas de Opera¸cão dos TPs (kV )
0, 6 25, 8 92, 4 362
1, 2 38 145 460
7, 2 48, 3 169 550
12 72, 5 242 765
15
Em termos práticos, na especifica¸cão de um TP, a sua tensão máxima de opera¸cão
pode ser considerada como sendo a que consta do quadro da tabela acima imedia-
tamente superior a tensão do circuito em que o TP será utilizado.

7. Polaridade: Num transformador (figura abaixo) diz-se que o terminal X1 do se-
cundário tem a mesma polaridade do terminal H1 do primário se, no mesmo instante,
H1 e X1 são positivos (ou negativos) em rela¸cão à H2 e X2, respectivamente.
No caso do TP, a polaridade não precisa ser levada em considera¸cão quando ele
alimenta somente volt´ımetros, relés de tensão, etc. Mas, quando ele alimenta ins-
trumentos elétricos cuja bobina de potencial é provida de polaridade relativa, como
watt´ımetros, medidores de energia elétrica, fas´ımetros, etc., então é extremamente
importante a considera¸cão da polaridade do TP: a entrada da bobina de potencial
destes instrumentos deve ser ligada ao terminal secundário do TP que corresponde
ao seu terminal primário que está ligado como entrada ao circuito principal.
Exemplo: Na figura acima, se o primário do TP for ligado ao circuito de modo que
H1 seja entrada, então a entrada das bobinas de potencial dos instrumentos será
ligada ao terminal X1 do secundário. Da mesma forma, H2 pode ser ligado como
entrada do primário, e então X2 é que será utilizado como entrada das bobinas de
potencial daqueles instrumentos elétricos.
Normalmente, os terminais dos enrolamentos primário e secundário dos TPs são
dispostos de tal forma que os terminais de mesma polaridade ficam adjacentes,
como mostra a figura à esquerda acima, e não em diagonal como mostra a figura à
direita acima.
8. Se um TP alimenta vários instrumentos elétricos, estes devem ser ligados em paralelo
a fim de que todos eles fiquem submetidos à mesma tensão secundária do TP.
9. Estando um TP alimentado, e havendo necessidade de se retirar todos os instrumentos
elétricos do seu secundário, lembra-se aqui que este enrolamento deve ficar aberto.
O fechamento do secundário de um TP através de um condutor de baixa impedância
provocará um curto-circuito, ou seja, uma corrente I2 demasiadamente elevada, e
conseqüentemente, também I1, provocando a danifica¸cão do TP e ainda uma poss´ıvel
perturba¸cão no sistema do circuito principal.
10. Quando se empregam TPs em medi¸cão de energia elétrica para fins de faturamento
a consumidor, é recomendável que estes TPs sejam utilizados exclusivamente para
alimentar o medidor ou medidores de energia elétrica da instala¸cão. Não deve ser
permitida a coloca¸cão de outros instrumentos ou dispositivos no secundário destes
TPs tais como volt´ımetros, relés, lâmpadas de sinaliza¸cão, etc.

3.4 Transformador de Corrente (TC)
A figura abaixo representa, esquematicamente, o transformador de corrente. O TC
tem n1 < n2 dando assim uma corrente I2 < I1, sendo por isto considerado na prática
como um elemento “redutor de corrente”, pois uma corrente elevada I1 é transformada
para uma corrente reduzida I2 de valor suportável pelos instrumentos elétricos usuais.
O enrolamento primário dos TCs é normalmente constitu´ıdo de poucas espiras (duas
ou três espiras, por exemplo) feitas de condutor de cobre de grande se¸cão. Há TCs em que
o próprio condutor do circuito principal serve como primário, sendo neste caso considerado
este enrolamento como tendo apenas uma espira.
Os TCs são projetados e constru´ıdos para uma corrente secundária nominal estabele-
cida de acordo com a ordem de grandeza da corrente do circuito em que o TC será ligado.
Assim, são encontrados no mercado TCs para: 200/5A, 1000/5A, etc., isto significando
que:
a. quando o primário é percorrido pela corrente nominal para a qual o TC foi constru´ıdo,
no secundário tem-se 5A;
b. quando o primário é percorrido por uma corrente menor ou maior do que a nominal,
no secundário tem-se também uma corrente menor ou maior do que 5A, mas na
mesma propor¸cão das correntes nominais do TC utilizado. Exemplo: se o primário
de um TC de 100/5A é percorrido por uma corrente de 84A, tem-se no secundário
4, 2A, se é percorrido por 106A, tem-se no secundário 5, 3A.
O quadro da figura abaixo mostra as correntes primárias nominais e as rela¸cões nomi-
nais padronizadas pela ABNT para os TCs fabricados em linha normal no Brasil.

Os TCs são projetados e constru´ıdos para suportarem, em regime permanente, uma
corrente maior do que a corrente nominal, sem que nenhum dano lhes seja causado. A
rela¸cão entre a corrente máxima suportável por um TC e a sua corrente nominal define o
“fator térmico”do TC.
Como os TCs são empregados para alimentar instrumentos elétricos de baixa im-
pedância (amper´ımetros, bobinas de corrente de watt´ımetros, bobinas de corrente de
medidores de energia elétrica, relés de corrente, etc.) diz-se que são transformadores de
for¸ca que funcionam quase em curto-circuito.
A corrente I1 surge no primário do transformador como uma conseqüência da corrente
I2 originada por solicita¸cão da carga posta no secundário dele. No transformador de
corrente, entretanto, a corrente I1 é originada diretamente por solicita¸cão da carga com
a qual o TC está em série, surgindo então a corrente I2 como uma conseqüência de I1,
independentemente do instrumento elétrico que estiver no seu secundário.
3.4.1 Rela¸cão Nominal
I1n
I2n
= Kc
É a rela¸cão entre os valores nominais I1n e I2n das correntes primária e secundária,
respectivamente, correntes estas para as quais o TC foi projetado e constru´ıdo. A “rela¸cão
nominal”é a indicada pelo fabricante na placa de identifica¸cão do TC. É chamada também
de “rela¸cão de transforma¸cão nominal”, ou simplesmente de “rela¸cão de transforma¸cão”,
sendo nas aplica¸cões práticas considerada uma constante para cada TC. Ela é muito
aproximadamente igual à rela¸cão entre as espiras:
I1n
I2n
= Kc = n2
n1
3.4.2 Rela¸cão Real
I1
I2
= Kr

É a rela¸cão entre o valor exato I1 de uma corrente qualquer aplicada ao primário do
TC e o correspondente valor exato I2 verificado no secundário dele. Em virtude de o TC
ser um equipamento eletromagnético, a cada I1 corresponde um I2 e como conseqüência,
um Kr:
I1
I2
= Kr ;
I1
I2
= Kr ;
I1
I2
= Kr
Como também, para uma mesma corrente I1 que percorre o primário, a cada carga
colocada no secundário do TC poderá corresponder um valor da corrente I2, e como
conseqüência, um Kr:
I1
I2
= Kr ; I1
I2
= Kr ; etc.
Estes valores de Kr são todos muito próximos entre si e também de Kc, pois os TCs são
projetados dentro de critérios especiais e são fabricados com materiais de boa qualidade
sob condi¸cões e cuidados também especiais.
Como não é poss´ıvel medir I2 e I1 com amper´ımetros (I1 tem normalmente valor
elevado), mede-se I2 e chega-se ao valor exato I1 através da constru¸cão do diagrama
fasorial do TC. Por isto é que a “rela¸cão real”aparece mais comumente indicada sob a
forma seguinte:
I1
I2
= Kr
3.4.3 Fator de Corre¸cão de Rela¸cão
Kr
Kc
= FCRc
É o fator pelo qual deve ser multiplicada a “rela¸cão de transforma¸cão”Kc do TC para
se obter a sua rela¸cão real Kr.
De imediato vê-se que a cada Kr de um TC corresponderá um FCRc. Em virtude
destas varia¸cões, determinam-se os valores limites inferior e superior do FCRc para cada
TC, sob condi¸cões especificadas, partindo-se da´ı para o estabelecimento da sua “classe de
exatidão”, conforme será visto a seguir.
Na prática lemos o valor da tensão I2 com um amper´ımetro ligado ao secundário do
TC e multiplicamos este valor lido por Kc para obtermos o valor da corrente primária,
valor este que representa o “valor medido”desta corrente primária, e não o seu valor exato
I1.
Exemplo: um TC de 200/5A tem o primário ligado em série com uma carga e o
secundário alimentando um amper´ımetro onde se lê: I2 = 3, 8A. Como a rela¸cão de
transforma¸cão é neste caso Kc = 40, considera-se que a corrente solicitada pela carga é:
KcI2 = 40 · 3, 8 = 152A
3.4.4 Diagrama Fasorial
O diagrama fasorial do TC, mostrado na figura abaixo, é o mesmo do TP e segue
o mesmo racioc´ınio para a sua constru¸cão, havendo, entretanto, uma simplifica¸cão a ser
levada em conta: como o primário do TC tem impedância muito baixa, a queda de tensão
neste enrolamento pode ser considerada desprez´ıvel, não aparecendo a sua representa¸cão
no diagrama fasorial:

U1 = E1 = 0
No exemplo citado anteriormente, o valor encontrado de 152A é o valor medido da
corrente primária do TC. Para determinar o valor verdadeiro I1 desta corrente, ter-se-á
de construir o diagrama fasorial deste TC como aparece na figura acima. Assim, para
fixar a idéia:
a. KcI2 é o valor medido da corrente primária;
b. |I1| = I1 é o valor verdadeiro ou exato da corrente primária obtido no diagrama
fasorial, o qual pode diferir ligeiramente de KcI2.
Ainda na figura acima, pode ser visto que o inverso de I2 está defasado de um ângulo
β em rela¸cão à I1. Num TC ideal este ângulo β seria zero.
Estas considera¸cões levam a concluir que o TC, ao refletir no secundário o que se passa
no primário, pode introduzir dois tipos de erros.
3.4.5 Erros do TC
Erro de Rela¸cão εc
valor relativo: εc = KcI2−|I1|
|I1|
valor percentual: ε%
c = KcI2−|I1|
|I1|
· 100
Quando εc e FCRc estão expressos em valores percentuais, há o seguinte relaciona-
mento entre eles:
ε%
c = 100 − FCR%
c
Da mesma forma que para o TP, os erros do TC são determinados na prática comparando-
o com um TC padrão idêntico a ele, de mesma rela¸cão de transforma¸cão nominal Kc,
porém sem erros, ou de erros conhecidos.

Esta expressão mostra a equivalência correta entre o erro de rela¸cão εc e o fator de
corre¸cão de rela¸cão FCRc, cujos valores indicados no paralelogramo de exatidão estão
perfeitamente coerentes com esta equivalência.
Para fixar a idéia, vamos dar um exemplo numérico. O primário de um TC de 200/5A,
sob ensaio é percorrido por uma certa corrente que faz surgir no secundário a corrente de
4, 96A. Constata-se depois que a tensão primária fora de exatamente 200A. Determinar:
Kc, Kr, FCRc e ε%
c .
Rela¸cão de Transforma¸cão Nominal: Kc = 200/5 = 40
Rela¸cão Real: Kr = 200/4, 96 = 40, 32
Fator de Corre¸cão de Rela¸cão: FCRc = 40, 32/40 = 1, 008 ou FCRc = 100, 8%
Erro de Rela¸cão: ε%
c = 100 − 100, 8 = −0, 8%
Sendo neste caso FCRc > 100%, então o erro cometido em rela¸cão à corrente primária
é por falta. Observar que o erro εc é negativo, o que comprova esta conclusão.
Erro de Fase ou Ângulo de Fase
É o ângulo de defasagem β existente entre I1 e o inverso de I2. Se o inverso de I2 é
adiantado em rela¸cão a I1, β é positivo. Em caso contrário, é negativo.
3.4.6 Classes de Exatidão dos TCs
Os erros de rela¸cão e de fase de um TC variam com a corrente primária e com o tipo
de carga colocada no seu secundário, além de sofrerem influência também das varia¸cões
da freqüência e da forma da onda, influência esta que não será analisada em virtude de
estas duas grandezas serem praticamente invariáveis nos sistemas elétricos atuais.
Tendo em vista estas considera¸cões, as normas estabelecem certas condi¸cões sob as
quais os TCs devem ser ensaiados para que possam ser enquadrados em uma ou mais das
três seguintes classes de exatidão: classe de exatidão 0, 3, 0, 6 e 1, 2.
Considera-se que um TC para servi¸co de medi¸cão está dentro de sua classe de exatidão
em condi¸cões especificadas quando, nestas condi¸cões, o ponto determinado pelo erro de
rela¸cão εc ou pelo fator de corre¸cão de rela¸cão FCRc e pelo ângulo de fase β estiver
dentro dos paralelogramos de exatidão especificados nas figuras a seguir correspondentes
à sua classe de exatidão, sendo que o paralelogramo interno (menor) refere-se a 100% da
corrente nominal, e o paralelogramo externo (maior) refere-se a 10% da corrente nominal.
No caso de TC com fator térmico nominal superior a 1, 0 o paralelogramo interno (menor)
refere-se também a 100% da corrente nominal multiplicada pelo fator térmica nominal.

As cargas padronizadas, acima referidas, estão relacionadas no quadro abaixo. É
interessante ressaltar que estas cargas não foram “criadas”aleatoriamente, mas sim tendo
em vista os tipos de instrumentos elétricos que são usualmente empregados no secundário
dos TCs, instrumentos aqueles com os quais tais cargas se assemelham em caracter´ısticas
elétricas.
Para melhor entendimento do paralelogramo de exatidão, suponhamos que um TC,
ensaiado com uma das cargas do quadro acima, apresentou:
a. com 100% da corrente nominal:
erro de rela¸cão: εc = −0, 2% o que corresponde ao FCRc = 100, 2%
ângulo de fase: β = 18

b. com 10% da corrente nominal:
erro de rela¸cão: εc = −0, 3% o que corresponde ao FCRc = 100, 3%
ângulo de fase: γ = 30
O ponto determinado pelos dois erros de cada ensaio fica dentro do respectivo para-
lelogramo de 100% e 10% da corrente nominal, correspondente à classe de exatidão 0, 6.
Então este TC será considerado de classe de exatidão 0, 6 para a carga de ensaio, embora
o erro de rela¸cão tenha sido de no máximo 0, 3%.
Se na placa de um TC está indicado: 0, 3B − 0, 1/B − 0, 2/B − 0, 5; 0, 6B − 1 isto
significa que:
1. o TC ensaiado com as cargas padronizadas B − 0, 1, B − 0, 2 e B − 0, 5 tem classe
de exatidão 0, 3, isto é, apresenta erro de rela¸cão −0, 3% ≤ εc ≤ 0, 3% e ângulo de
fase β tal que o ponto correspondente a estes erros fica dentro dso paralelogramos
representativos da classe de exatidão 0, 3%;
2. ensaiado com a carga padronizada B − 1 tem classe de exatidão 0, 6.
Na designa¸cão da ABNT aquela indica¸cão na placa do TC seria representada por
0, 3 − C12, 5; 0, 6 − C25 .
O quadro abaixo mostra como selecionar a exatidão adequada para um TC tendo em
vista a sua aplica¸cão nas diferentes categorias de medi¸cões.
3.4.7 Influência da Corrente de Excita¸cão nos Erros do TC
Conforme pode ser visto no diagrama fasorial, a corrente de excita¸cão I0 é a causa
essencial dos erros de rela¸cão e de fase do TC. Se ela não existisse, caso de TC ideal, os
fasores I1 e −
n2
n1
· I2 seriam sempre coincidentes, em fase e em módulo.
Na prática, os fabricantes procuram reduzir ao m´ınimo poss´ıvel a corrente de excita¸cão
utilizando núcleos de forma toróidal sem entre-ferro (figura abaixo), feitos de ligas espe-
ciais de alta permeabilidade magnética e perdas reduzidas, projetados para trabalharem
sob densidade de fluxo muito baixa, cerca de 0, 1 tesla (1000 gauss), enquanto que nos
transformadores de for¸ca esta densidade atinge de 1, 2 a 1, 5 tesla (12000 a 15000 gauss).

Apesar destas providências, quando o TC é posto em opera¸cão, a corrente de excita¸cão
sofre varia¸cões por influência das duas grandezas seguintes, causando em conseqüência
varia¸cões nos seus erros de rela¸cão e de fase: corrente primária e carga posta no secundário
do TC.
3.4.8 Influência da Corrente Primária nos Erros do TC
A corrente de excita¸cão dos transformadores, inclusive dos TPs, é uma grandeza con-
siderada praticamente constante para cada transformador, desde vazio até plena carga,
sendo o seu módulo I0 e a sua dire¸cão θ0 determinados através de um ensaio em vazio.
Nos transformadores de corrente isto não ocorre. A corrente de excita¸cão não é cons-
tante para cada TC, nem em módulo nem em dire¸cão, pois há de se levar em conta, neste
tipo de transformador, a influência importante que tem a não linearidade magnética do
material de que são feitos os núcleos. A figura abaixo dá uma idéia da correla¸cão entre
as varia¸cões das duas correntes, a primária e a de excita¸cão, lembrando que a primária
depende da carga com a qual o TC está ligado em série:
a. quando a corrente primária é 100% da nominal, a de excita¸cão é cerca de 1% dela;
b. quando a corrente primária é 50% da nominal, a de excita¸cão é cerca de 0, 8% desta;
c. quando a corrente primária é de 10% da nominal, a de excita¸cão é cerca de 0, 3%desta;
e assim sucessivamente.

Com estas aprecia¸cões, pode-se sentir no diagrama fasorial que, para valores meno-
res da corrente primária, a corrente de excita¸cão terá então influência mais acentuada
tornando maiores os erros de rela¸cão e de fase.
Por isto é que as normas técnicas permitem que, na determina¸cão da classe de exa-
tidão de um TC, este apresente erros maiores quando ensaiado com 100% dela, conforme
mostram os paralelogramos de exatidão. Os lados do paralelogramo externo (maior) po-
deriam ser admitidos como o triplo ou o quádruplo ou o qu´ıntuplo, etc., respectivamente,
dos lados do paralelogramo interno (menor). Eles foram estabelecidos como o dobro a fim
de que os fabricantes se esmerem em fornecer produtos cada vez mais de melhor quali-
dade, de melhor desempenho quanto à exatidão, e os usuários não tenham incertezas nos
valores medidos, isto é, que os valores medidos sejam realmente corretos.
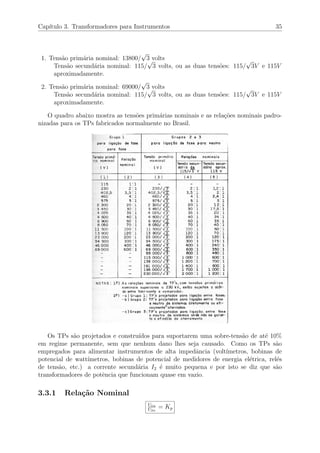
A rela¸cão nominal ou rela¸cão de transforma¸cão dos TCs modernos é muito aproxima-
damente igual à rela¸cão entre as espiras:
I1n
I2n
= Kc =
n2
n1
As varia¸cões dos erros de rela¸cão e de fase do TC em fun¸cão das varia¸cões da corrente
primária podem ser interpretadas matematicamente considerando a expressão acima como
correta.
Na figura abaixo, projetando todos os fasores sobre I1:
|I1| = Kc|I2| · cos β + |I0| · cos [90 − (δ + α + β)]
Como o ângulo β é muito pequeno (no máximo chega a 1o
), pode ser considerado
desprez´ıvel diante dos outros valores, e a expressão anterior toma a forma:
|I1| = Kc|I2| + |I0| · sin (δ + α)
Ou ainda:
Kc|I2| − |I1|
|I1|
= −
|I0|
|I1|
· sin (δ + α)

O primeiro membro da expressão acima representa o erro relativo εc, o qual será
considerado aqui em módulo. E como os módulos dos fasores indicados representam
realmente os valores eficazes das respectivas correntes podemos escrever:
εc =
I0
I1
· sin (δ + α)
Do mesmo diagrama podemos escrever:
tgβ =
|I0| · cos [90 − (δ + α + β)]
Kc|I2| cos β
Como β é pequeno, e tendo em vista o que foi dito acima, para efeito de cálculo a
expressão acima pode ser escrita na forma simplificada:
Para uma mesma carga posta no secundário do TC e tendo em vista o que foi dito antes,
as expressões desta sessão mostram que os erros εc e β aumentam quando I1 decresce.
Como exemplo elucidativo, vamos considerar dois valores para I1:
a. Para I1 = I1n → I0 = 0, 001I1n , então:
εc = 0, 01 sin (δ + α)
β = 0, 01 cos (δ + α)
b. Para I1 = 0, 1I1n → I0 = 0, 003I1n , então:
εc = 0, 03 sin (δ + α)
β = 0, 03 cos (δ + α)
Donde se conclui claramente que:
ε > εc
β > β
De tudo isto se conclui que é importante que o TC seja de corrente nominal o mais
próximo do valor da corrente da instala¸cão em que está inserido. Se a corrente nominal
do TC é muito maior do que a corrente da instala¸cão, ele estará introduzindo também
uma incerteza muito maior nos valores medidos.
3.4.9 Influência da Carga Secundária do TC nos seus Erros
Já foi dito anteriormente que a corrente secundária do TC depende unicamente da
corrente primária, sendo independente da impedância do instrumento elétrico posto no
seu secundário. Entretanto, se esta impedância ultrapassa os valores permiss´ıveis, tendo
em vista a potência máxima com a qual o TC teve a sua classe de exatidão determinada,
então os erros introduzidos por ele poderão ser bem mais elevados do que os levantados
nos ensaios e garantidos pelo fabricante.
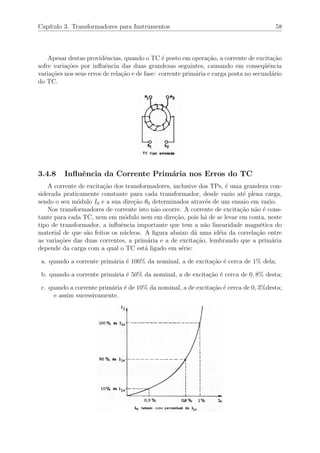
Para se entender bem esta influência, vamos considerar que o primário do TC seja
percorrido por uma corrente fixada I1 nas três situa¸cões que serão analisadas abaixo:

1. Para uma certa impedância Z posta no secundário do TC, haverá uma corrente I2 e
os erros εc e β correspondentes são indicados pelas expressões da sessão anterior.
2. A impedância Z aumenta em módulo para Z , conservando o mesmo ângulo de fase
θ2, conforme está no diagrama fasorial da sessão anterior: para que a corrente I2
se mantenha a mesma (ou aproximadamente a mesma) a tensão secundária U2 terá
de aumentar para U2. Mas, para isto, E2 terá de aumentar para E2 e o fluxo Φ
para Φ . Como a corrente I0 é que origina o fluxo Φ, então também aumentará para
I0. Em conseqüência, os erros εc e β aumentarão, como mostram as expressões da
sessão anterior. Em resumo: os erros do TC aumentam quando a impedância posta
no secundário aumenta.
3. A impedância Z não varia em módulo, porém varia o seu ângulo de fase θ2: portanto,
a corrente I0 não sofrerá varia¸cão. Observando as expressões da sessão passada,
vamos analisar as quatro possibilidades seguintes:
a. θ2 tende para zero: εc decresce e β cresce.
b. θ2 tem um valor tal que δ + α = 90o
: εc atinge o máximo valor e β é zero.
c. θ2 tem um valor tal que δ = 90o
: εc é positivo, mas β é negativo.
d. No caso particular de um TC muito bem projetado e constru´ıdo, tendo a
reatância x2 = 0, e sendo a impedância Z um resistor, poder-se-á ter:
θ2 = δ = 0
Então, as expressões da sessão anterior tornar-se-iam:
εc =
|I0|
|I1| · sin α
β =
|I0|
|I1| · cos α
Mas no diagrama fasorial, vê-se que:
|I0| · sin α = |Ip| e |I0| · cos α = |Iµ|
Assim, as expressões anteriores tomam forma:
εc =
|Ip|
|I1|
e β =
|Iµ|
|I1|
Em virtude da expressão acima, diz-se na prática que a componente de perdas
Ip Da corrente de excita¸cão é a responsável pelo erro de rela¸cão, e a componente
de magnetiza¸cão Iµ é a responsável pelo erro de fase.
Estas análises sobre o comportamento do TC, em face da impedância posta no
seu secundário, servem de alerta ao usuário quanto à limita¸cão da resistência
dos condutores elétricos que são utilizados para liga¸cão do secundário do TC aos
instrumentos elétricos que ele alimenta, sobretudo quando estes instrumentos
são colocados a uma distância considerável.

3.4.10 O Secundário de um TC Nunca Deve Ficar Aberto
Quando o primário de um TC está alimentado, o seu secundário nunca deve ficar
aberto. No caso de se necessitar retirar o instrumento do secundário do TC, este enrola-
mento deve ser curto-circuitado através de um fio condutor de baixa impedância, um fio
de cobre por exemplo. Vejamos as razões desta precau¸cão: como já foi dito, a corrente
I1 é fixada pela carga ligada ao circuito externo; se I2 = 0, isto é, secundário aberto, não
haverá o efeito desmagnetizante desta corrente e a corrente de excita¸cão I0 passará a ser
a própria corrente I1, originando em conseqüência um fluxo Φ muito elevado no núcleo.
Conseqüências desta imprecau¸cão:
a. Aquecimento excessivo causando a destrui¸cão do isolamento, podendo provocar con-
tato do circuito primário com o secundário e com a terra.
b. Uma f.e.m. induzida E2 de valor elevado, com iminente perigo para o operador.
c. Mesmo que o TC não se danifique, a este fluxo Φ elevado corresponderá uma mag-
netiza¸cão forte no núcleo, o que alterará as suas caracter´ısticas de funcionamento e
precisão.
Por este motivo, nunca se usa fus´ıvel no secundário dos TCs.
3.4.11 Fator de Corre¸cão de Transforma¸cão (FCTc) do TC
Quando o TC está alimentando apenas amper´ımetro, o FCRc é o único que tem efeito
nos valores medidos. Mas, quando o TC alimenta instrumentos cuja indica¸cão depende
dos respectivos módulos da tensão e da corrente a ele aplicadas e também do ângulo de
defasagem entre estas duas grandezas como no caso de watt´ımetros e medidores de energia
elétrica, então o FCRc e o ângulo de fase β têm efeito simultâneo nos valores medidos, e
por isto devem ser ambos levados em considera¸cão na análise dos resultados.
Com isto chega-se ao “fator de corre¸cão de transforma¸cão”FCTc que é definido da
seguinte maneira: fator pelo qual se deve multiplicar a leitura indicada por um watt´ımetro,
ou por um medidor de energia elétrica, cuja bobina de corrente é alimentada através do
referido TC, para corrigir o efeito combinado do fator de corre¸cão de rela¸cão FCRc e do
ângulo de fase β.
A montagem da figura seguinte esquematiza o que acima foi dito.

As normas técnicas definem o tra¸cado dos paralelogramos de exatidão baseando-se
no FCTc e na carga medida no primário do TC (carga M na figura anterior), para a
qual estabelecem que o fator de potência deve ser indutivo e ter um valor compreendido
entre 0, 6 e 1. Fica então entendido que a exatidão do TC, indicada na sua placa de
identifica¸cão, somente é garantida para cargas medidas daquele tipo, isto é, com fator de
potência indutivo entre 0, 6 e 1.
Para qualquer fator de corre¸cão da rela¸cão FCRc conhecido de um TC, os valores
limites positivos e negativos do ângulo de fase β em minutos são expressos por:
β = 2600 (FCRc − FCTc)
onde o fator de corre¸cão da transforma¸cão FCTc deste TC assume os seus valores máximo
e m´ınimo.
Justamente, a partir da expressão acima é que se constroem os dois paralelogramos
de exatidão correspondentes a cada classe, pois, fixado um valor numérico para o FCTc,
vê-se que esta expressão representa a equa¸cão de uma reta. O FCTc pode ter quatro
valores em cada classe de exatidão:
a. Na classe de exatidão 0, 3:
a.1. 1, 003 e 0, 997 para 100% da corrente nominal
a.2. 1, 006 e 0, 994 para 10% da corrente nominal
b. Na classe de exatidão 0, 6:
b.1. 1, 006 e 0, 994 para 100% da corrente nominal
b.2. 1, 012 e 0, 988 para 10% da corrente nominal
c. Na classe de exatidão 1, 2:
c.1. 1, 012 e 0, 988 para 100% da corrente nominal
c.2. 1, 024 e 0, 976 para 10% da corrente nominal
Para se tra¸car os dois paralelogramos que definem a classe de exatidão de um TC,
procede-se da seguinte maneira:
Paralelogramo Menor: atribui-se ao FCTc o seu valor máximo nesta classe de exatidão
correspondente a 100% da corrente nominal e faz-se variar o FCRc desde o seu
limite superior até o limite inferior, obtendo-se assim os valores negativos de β,
podendo-se então tra¸car um lado inclinado da figura. Em seguida, atribui-se ao
FCTc o seu valor m´ınimo e faz-se novamente o FCRc variar, obtendo-se agora os
valores positivos de β e conseqüentemente o outro lado inclinado da figura.
Paralelogramo Maior: atribui-se ao FCTc o seu valor máximo nesta classe de exatidão
correspondente a 10% da corrente nominal e repete-se o mesmo procedimento utili-
zado para o tra¸cado do paralelogramo menor.

3.4.12 Classifica¸cão dos TCs
Conforme a disposi¸cão dos enrolamentos e do núcleo, os TCs podem ser classificados
nos seguintes tipos:
TC tipo enrolado: TC cujo enrolamento primário constitu´ıdo de uma ou mais espiras,
envolve mecanicamente o núcleo do transformador.
TC tipo barra: TC cujo primário é constitu´ıdo por uma barra, montada permanente-
mente através do núcleo do transformador.
TC tipo janela: TC sem primário próprio, constru´ıdo com uma abertura através do
núcleo, por onde passará um condutor do circuito primário, formando uma ou mais
espiras.
TC tipo bucha: tipo especial de TC tipo janela, projetado para ser instalado sobre uma
bucha de um equipamento elétrico, fazendo parte integrante deste.
TC de núcleo dividido: tipo especial de TC tipo janela, em que parte do núcleo é
separável ou basculante, para facilitar o enla¸camento do condutor primário. O
amper´ımetro tipo “alicate”nada mais é do que um TC de núcleo dividido, o qual
possibilita medir a corrente sem a necessidade de abrir o circuito para colocá-lo em
série.
Conforme a finalidade de aplica¸cão, os TCs podem ser classificados nos dois tipos
seguintes: TC para medi¸cão e TC para prote¸cão.

3.4.13 TC de Vários Núcleos
É muito freqüente na prática (sobretudo em circuitos de alta tensão) a utiliza¸cão de
TC de vários núcleos. Trata-se de TC com vários enrolamentos secundários isolados
separadamente e montados cada um em seu próprio núcleo, formando um conjunto com
um único enrolamento primário, cujas espiras (ou espira) enla¸cam todos os secundários.
Um dos secundários é destinado à medi¸cão e os outros (ou o outro) são destinados à
prote¸cão.
É importante observar que, neste tipo de TC, todos os secundários que não estiverem
alimentando instrumentos elétricos deverão permanecer curto-circuitados. O primário é
um elemento comum a todos os núcleos. Mas cada núcleo com o seu secundário próprio
atua como um TC independente dos outros.
3.4.14 TC de Múltipla Rela¸cão de Transforma¸cão
Os TCs podem ser constru´ıdos para uma única rela¸cão de transforma¸cão ou para
múltipla rela¸cão de transforma¸cão, existindo neste segundo caso quatro tipos de TCs que
passarão a ser analisados.
TC com vários enrolamentos no primário (liga¸cão série/paralela no primário): A figura
abaixo mostra um TC deste tipo, em que o secundário tem um número fixo N2
de espiras e o primário é constitu´ıdo de várias bobinas idênticas entre si, cada
uma tendo N espiras, as quais podem ser combinadas em série ou em paralelo,
permitindo várias rela¸cões de transforma¸cão. Por exemplo: consideremos que um
TC com a possibilidade de três correntes primárias nominais: 50A, 100A e 200A.
Os esquemas abaixo mostram as combina¸cões que devem ser feitas no primário para
a obten¸cão das três rela¸cões de transforma¸cão nominais. Como pode ser visto, o
número de ampéres-espiras permanece constante em todas as corrente nominais.
Neste exemplo, temos 200N ampéres-espiras: para 50/5A, para 100/5A e para
200/5A, nas condi¸cões nominais. Diz-se na prática que estes TCs são de rela¸cões
nominais múltiplas com liga¸cão série/paralela no enrolamento primário.

TC com várias deriva¸cões no secundário: A figura abaixo mostra um TC deste tipo,
em que o primário é que tem agora um número fixo N de espiras e o secundário
tem duas deriva¸cões que permitem utilizar o TC como 50/5A ou como 100/5A. A
se¸cão do condutor do primário é dimensionada tendo em vista a maior das correntes
para as quais um TC deste é projetado; no exemplo em tela: 100A. Como pode
ser visto, o número de ampéres-espiras não é o mesmo em todas as rela¸cões de
transforma¸cão nominais. Neste exemplo em discussão: na rela¸cão de 50/5A ter´ıamos
50N ampéres-espiras e na rela¸cão de 100/5A ter´ıamos 100N ampéres-espiras, nas
condi¸cões nominais.
TC com vários enrolamentos no primário e várias deriva¸cões no secundário: Os dois
tipos de TCs discutidos anteriormente podem ser englobados neste terceiro tipo,
conseguindo-se com isto um TC de muitas possibilidades quanto a rela¸cões de trans-
forma¸cão. A figura abaixo mostra, esquematicamente, a disposi¸cão dos enrolamen-
tos de acordo com os TCs existentes na prática. Nos TCs com várias deriva¸cões no
secundário, não podem ser utilizadas, ao mesmo tempo, duas ou mais deriva¸cões
para alimentarem instrumentos elétricos. Somente pode ser utilizada uma das de-
riva¸cões, permanecendo as outras abertas (não curto-circuitadas) a fim de que estas
não interfiram nos resultados.

TC com vários enrolamentos no secundário (liga¸cão série/paralela no secundário): Trata-
se de um TC especial (para fins de prote¸cão), e por isto constru´ıdo somente sob
solicita¸cão espec´ıfica do comprador interessado, o qual o aplicará em circuitos bem
definidos da sua instala¸cão. A figura abaixo mostra um TC deste tipo em que o se-
cundário tem dois enrolamentos com N2 espiras, podendo isto permitir três rela¸cões
de transforma¸cão nominais. Para fixar idéia, vamos supor que seja um TC para
100/5A, 100/2, 5A e 100/10A. Os esquemas abaixo mostram as respectivas liga¸cões
para estas rela¸cões. Na liga¸cão de 100/5A apenas um dos enrolamentos secundários
deve ser utilizado na alimenta¸cão de instrumentos elétricos permanecendo o ou-
tro (ou os outros) enrolamento aberto (não curto-circuitado) afim de não produzir
interferência na medi¸cão.
3.4.15 Considera¸cões Sobre os TCs com Deriva¸cão no Secundário
e Liga¸cão Série/Paralela no Primário
Conforme foi visto na sessão anterior, a quantidade de ampéres-espiras não é cons-
tante num TC com deriva¸cões no secundário nas respectivas rela¸cões nominais. Em
conseqüência, a exatidão do TC não é garantida a mesma em todas as rela¸cões nomi-
nais obtidas com as deriva¸cões. Normalmente, a classe de exatidão especificada pelo
comprador para TC com deriva¸cões no secundário é garantida pelo fabricante apenas no
funcionamento com o maior número de espiras. Os TCs destinados à prote¸cão podem ser
aceitos, e até especificados pelo usuário, tendo muitas deriva¸cões no secundário, pois, a
classe de exatidão desses TCs é 10, isto é, o erro de rela¸cão pode ser até 10%, não havendo

limite para o ângulo de fase. Entretanto, os TCs para medi¸cão têm classes de exatidão
mais exigente e por isto duas considera¸cões serão feitas a seguir:
1. Em medi¸cão para fins de faturamento devem ser preferidos TCs com apenas uma
rela¸cão nominal, ou se desejar TCs com duas ou três rela¸cões nominais estes de-
vem ser especificados com liga¸cão série/paralela no primário (sem deriva¸cão no se-
cundário) o que permitirá exigir do fabricante a garantia da exatidão em todas as
rela¸cões nominais.
2. Em medi¸cão de controle (sem finalidade de faturamento) podem ser empregados
TCs com deriva¸cões no secundário, sendo aconselhável que eles sejam especificados
de modo que as deriva¸cões extremas sejam tais que o quociente entre as rela¸cões
nominais com elas obtidas não seja superior a 2. Exemplo: um TC com deriva¸cões
no secundário, cuja deriva¸cão m´ınima permite a rela¸cão nominal 400/5A, deve ter
como deriva¸cão máxima a que permite a rela¸cão nominal 800/5A, podendo entre
estas duas extremas existirem outras deriva¸cões tais como as correspondentes a
500/5A, 600/5A e 700/5A.
3.4.16 Como Especificar um TC para Medi¸cão
Para especificar corretamente um TC, é necessário antes de tudo saber-se qual será a
finalidade da sua aplica¸cão, pois isto definirá a classe de exatidão, conforme visto anteri-
ormente.
A carga nominal do TC será estabelecida tendo em vista as caracter´ısticas (em termos
de perdas elétricas internas) dos instrumentos elétricos que serão inseridos no secundário,
caracter´ısticas estas que são normalmente fornecidas pelos seus fabricantes ou poderão ser
determinadas em laboratório através de ensaios apropriados. O quadro da figura abaixo
indica, a t´ıtulo de referência, a ordem de grandeza das perdas da bobina de corrente de
alguns instrumentos elétricos que são utilizados com TCs, em condi¸cões de 5A, 60Hz.
É poss´ıvel, partindo da´ı, chegar-se às caracter´ısticas Z, R e L de cada bobina, caso se
deseje. Convém aqui lembrar que para a bobina de corrente dos medidores de energia
elétrica, que as perdas não deverão exceder 2W e 2, 5V A. Os ensaios devem ser feitos em
condi¸cões nominais.
Para fixar idéia na especifica¸cão de TCs, vamos dar dois exemplos.

Exemplo 1
Especificar um TC para medi¸cão de energia elétrica para faturamento a um consumidor
energizado em 69kV , cuja corrente na linha chegará a cerca de 80A no primeiro ano de
funcionamento, podendo atingir cerca de 160A a partir do segundo ano. Os instrumentos
elétricos que serão empregados, abaixo indicados, ficarão a 25m do TC e serão ligados ao
secundário deste através de fio de cobre No
12AWG:
b. Medidor de kvar, espec´ıfico para energia reativa, sem indicador de demanda máxima.
Solu¸cão:
a. Classe de exatidão: o quadro indica 0, 3.
b. Carga nominal do TC: os fabricantes dos instrumentos elétricos que serão utilizados
forneceram o seguinte quadro de perdas em 5A, 60Hz:
Da´ı, chega-se a:
S = (9, 4)2 + (1, 6)2 ∴ S = 9, 54V A
Com este resultado, e consultando o quadro da figura de cargas nominais, vê-se
que o TC deve ser de carga nominal pelo menos de 12, 5V A que é a carga pa-
dronizada imediatamente superior a 9, 54V A. A especifica¸cão deste TC, do ponto
de vista elétrico, pode então ter seguinte enunciado: Transformador de corrente
para medi¸cão, correntes primarias nominais 100x200A (liga¸cão série/paralela no
primário), rela¸cões nominais 20x40 : 1, 60Hz, carga nominal ABNT C12, 5, classe
de exatidão ABNT 0, 3−C12, 5 (ou ANSI 0, 3B−0, 1/B−0, 2/B−0, 5), fator térmico
1, 2, para uso exterior (ou interior, conforme for o caso), n´ıvel de isolamento: tensão
nominal 69kV , tensão máxima de opera¸cão 72, 5kV , tensões suportáveis nominais
à freqüência industrial e de impulso atmosférico: 140kV e 350kV , respectivamente.
Exemplo 2
Especificar um TC para medi¸cão de energia elétrica e controle, sem finalidade de
faturamento, sabendo que a tensão entre fases do circuito é 13, 8kV e que a corrente na
linha chegará no máximo a 80A. Os instrumentos elétricos que serão empregados, abaixo
indicados, ficarão a 25m do TC e serão ligados ao secundário deste através de fio de cobre
No
12AWG:

a. Medidor de kWh com indicador de demanda máxima.
b. Medidor de kWh, sem indicador de demanda máxima, acoplado a um autotransfor-
mador de defasamento, servindo assim para medir kvarh.
c. Watt´ımetro.
d. Var´ımetro.
e. Amper´ımetro.
f. Fas´ımetro.
Solu¸cão:
a. Classe de exatidão: o quadro da classe de exatidão indica 0, 6 ou 1, 2 (a optar pelo
comprador).
b. Carga nominal do TC: os fabricantes dos instrumentos elétricos que serão utilizados
forneceram o seguinte quadro de perdas em 5A, 60Hz:
Da´ı, chega-se a:
S = (14, 8)2 + (8, 3)2 ∴ S = 16, 97V A
Com este resultado, e consultando o quadro da figura de cargas nominais, vê-se
que o TC deve ser de carga nominal pelo menos de 25V A que é a carga padroni-
zada imediatamente superior a 16, 97V A. A especifica¸cão deste TC, do ponto de
vista elétrico, pode então ter seguinte enunciado: Transformador de corrente para
medi¸cão, corrente primaria nominal 100A, rela¸cão nominal 20 : 1, 60Hz, carga no-
minal ABNT C25, classe de exatidão ABNT 0, 6 − C25 (ou ANSI 0, 6B − 0, 1/B −
0, 2/B − 0, 5/B − 1), fator térmico 1, 5, para uso exterior (ou interior, conforme for
o caso), n´ıvel de isolamento: tensão nominal 13, 8kV , tensão máxima de opera¸cão
15kV , tensões suportáveis nominais à freqüência industrial e de impulso atmosférico:
36kV e 110kV , respectivamente.

Observa¸cões
1. Ressaltamos que os dois exemplos dados servem apenas como orienta¸cão de dimensi-
onamento. Para cada caso, devem considerados os valores corretos das perdas dos
instrumentos e dos condutores que serão utilizados no secundário do TC.
2. Nos dois exemplos dados, pode-se observar que há uma influência considerável dos
fios de cobre que ligam os instrumentos ao secundário do TC, e isto deve ser bem
analisado nas instala¸cões reais. Se as perdas nestes fios não tivessem sido levadas
em considera¸cão, a potência no secundário do TC seria:
No exemplo 1: S = (2, 8)2 + (1, 6)2 ∴ S = 3, 23V A e o TC seria especificado
então erradamente como 0, 3 − C5, 0 e não como 0, 3 − C12, 5 que é o correto.
No exemplo 2: S = (8, 2)2 + (8, 3)2 ∴ S = 11, 6V A e o TC seria especificado
então erradamente como 0, 6 − C12, 5 e não como 0, 6 − C25 que é o correto.
3. Se há possibilidade, no futuro, de coloca¸cão de mais outros instrumentos no secundário
do TC, então é aconselhável superdimensioná-lo um pouco. Assim, o TC do exemplo
1 passaria a ser 0, 3 − C25 e o do exemplo 2, 0, 6 − C50 a fim de que fosse poss´ıvel
utilizá-lo também em medi¸cão para faturamento.
3.4.17 TCs para Prote¸cão
Embora todos os TCs tenham o mesmo princ´ıpio f´ısico de funcionamento e sejam cons-
titu´ıdos basicamente dos mesmos elementos, há a se levar em considera¸cão caracter´ısticas
bem marcantes que lhes são impostas no projeto e constru¸cão em termos de tipos de
núcleos e tipos de enrolamentos primário e secundário, as quais dividem os TCs em dois
grupos bem distintos quanto à finalidade de utiliza¸cão adequada: TCs para medi¸cão e
TCs para prote¸cão (para servi¸co de relés).
Os TCs para medi¸cão não devem ser utilizados para prote¸cão, como também os cons-
tru´ıdos para prote¸cão não devem ser utilizados para medi¸cão, sobretudo se esta medi¸cão
é de energia elétrica para fins de faturamento a consumidor. Esta precau¸cão é baseada
nas duas caracter´ısticas seguintes:
Classe de Exatidão: Os TCs para medi¸cão têm classe de exatidão 0, 3 − 0, 6 − 1, 2. Para
classificá-los, são considerados os erros de rela¸cão e de fase levantados nos ensaios.
Os TCs para prote¸cão têm classe de exatidão 10, onde é levado em considera¸cão
apenas o erro de rela¸cão, uma vez que, na prote¸cão, o que interessa é o efeito
produzido nos relés pelo módulo da corrente secundária como fun¸cão do módulo da
corrente primária, não tendo a´ı o erro de fase nenhuma influência.
Considera-se que um TC para servi¸co de prote¸cão está dentro da sua classe de
exatidão, em condi¸cões especificadas, quando, nestas condi¸cões, o seu erro de rela¸cão
percentual não for superior a 10%, desde a corrente nominal até uma corrente igual
a 20 vezes o valor da corrente nominal.
Circuito Magnético: O núcleo dos TCs para medi¸cão é feito de material de elevada
permeabilidade magnética (pequena corrente de excita¸cão, pequenas perdas, baixa
relutância) trabalhando sob condi¸cões de baixa indu¸cão magnética (cerca de 0, 1

tesla). Mas, eles entram em satura¸cão logo que a indu¸cão magnética cresce para
0, 4 a 0, 5 tesla, o que corresponde à corrente primária crescer para cerca de quatro
vezes o seu valor nominal. Mesmo que a corrente primária ultrapasse esta ordem
de grandeza e atinja valores excessivos, ela reflete no secundário uma corrente que
chega no máximo a cerca de quatro vezes o valor nominal desta, conforme mostra a
curva 1 da figura abaixo.
O núcleo dos TCs para prote¸cão é feito de material que não tem a mesma permea-
bilidade magnética, porém somente entra em satura¸cão para valores muito elevados
do fluxo (indu¸cão magnética elevada), correspondentes a uma corrente primária de
cerca de 20 vezes o valor nominal desta, conforme mostra a curva 2 da figura acima.
Nos instrumentos de medi¸cão uma corrente desta ordem de grandeza poderia dani-
ficá-los, enquanto que os relés podem perfeitamente suportá-la desde que são pre-
vistos para isto. Se um TC para medi¸cão é utilizado para alimentar relés, estes
muito certamente não entrarão em funcionamento na ocasião necessária (ocasião de
curto-circuito, por exemplo), pois entrando o TC em satura¸cão a corrente secundária
poderá não ser suficiente para sensibilizá-los convenientemente.
Por exemplo: um relé a tempo inverso que deve funcionar num tempo t1 (figura
abaixo) quando a corrente for 6 vezes a corrente nominal, será nestas condi¸cões
(quando alimentado através de TC para medi¸cão) sensibilizado como se a corrente
fosse cerca de 4 vezes a corrente nominal, mesmo que aquela corrente atingisse 5 ou
6 ou mais vezes a corrente nominal, entrando assim em funcionamento num tempo
t2 > t1, o que afetaria sensivelmente a seletividade com outros relés da retaguarda,
comprometendo desta forma a prote¸cão de todo o sistema.

Classifica¸cão dos TCs para Prote¸cão
Os TCs para prote¸cão são agrupados, tendo em vista a impedância do enrolamento
secundário, em duas classes:
Transformador de Corrente Classe B: TC que possui baixa impedância interna, isto
é, aquele cuja reatância de dispersão do enrolamento secundário possui valor des-
prez´ıvel. Constituem exemplos: os TCs de núcleo toróidal com enrolamento se-
cundário uniformemente distribu´ıdo.
Transformador de Corrente Classe A: TC que possui alta impedância interna, isto é,
aquele cuja reatância de dispersão do enrolamento secundário possui valor apreciável.
Nesta classe se enquadram todos os TCs exceto os que são definidos como classe B.
Especifica¸cão dos TCs para Prote¸cão
No Brasil, os TCs para prote¸cão devem satisfazer às duas condi¸cões seguintes:
1. Somente devem entrar em satura¸cão para uma corrente de valor acima de 20 vezes a
sua corrente nominal.
2. Devem ser de classe de exatidão 10, isto é, o erro de rela¸cão percentual não deve
exceder 10% para qualquer valor da corrente secundária, desde 1 a 20 vezes a corrente
nominal, e qualquer carga igual ou inferior à nominal.
A primeira condi¸cão leva ao estabelecimento da tensão secundária nominal, a qual
pode ser definida como sendo a tensão que aparece nos terminais da carga nominal posta
no secundário do TC para prote¸cão quando a corrente que a percorre é igual a 20 vezes
o valor da corrente secundária nominal, ou seja, quando a corrente secundária é 100A.
A cada carga nominal para TC padronizada pela ABNT corresponde então uma tensão
secundária nominal para TC para prote¸cão, a qual é obtida multiplicando-se por 100 a
impedância daquela carga nominal.
Na especifica¸cão de um TC para prote¸cão é necessário indicar se ele deve ser classe
A ou B, como também a tensão secundária nominal que o usuário deseja para ele. Não
é necessário citar a classe de exatidão, uma vez que no Brasil somente há a classe de
exatidão 10.
Exemplo 1: Um TC para prote¸cão B200 significa:

a. TC de classe de exatidão 10.
b. TC de classe B, isto é, de baixa impedancia interna.
c. Tensão secundária nominal 200V (está implicito que a carga secundária nominal
deve ser C50 cuja impedância é 2Ω, pois: V = 20 · 5 · 2 = 200V ).
Exemplo 2: Um TC para prote¸cão A400 significa:
a. TC de classe de exatidão 10.
b. TC de classe A, isto é, de alta impedancia interna.
c. Tensão secundária nominal 400V (está implicito que a carga secundária nominal
deve ser C100 cuja impedância é 4Ω, pois: V = 20 · 5 · 4 = 400V ).
Levando em conta o quadro de cargas nominais dos TCs, foi elaborado o quadro da fi-
gura abaixo onde são mostrados os valores das tensões secundárias nominais normalizadas
no Brasil, como também os vários tipos de TCs para prote¸cão das classes A e B.
Deve ficar entendido que, quando se está especificando um TC para prote¸cão que vai
ser adquirido, o dimensionamento da sua tensão secundária nominal é feito tendo-se em
conta o valor da impedância máxima Zm que poderá vir a ser imposta ao seu secundário
quando ele for utilizado na instala¸cão:
Zm = (Rr + 2r)2
+ (Xr)2
onde se tem a considerar:
Rr: resistência própria do relé
Xr: reatância própria do relé
r: resistência do condutor que liga o secundário do TC ao relé (2r é a resistência total)
Esta impedância máxima Zm deve ser relacionada à impedância nominal Z da carga
padronizada correspondente a tensão secundária nominal que terá de especificar:

Z ≥ Zm
Como também, ao se instalar um TC para prote¸cão, que já está dispon´ıvel na con-
cessionária, os condutores secundários devem ser corretamente dimensionados, em termos
de resistência máxima rm permiss´ıvel, tendo em conta a impedância Z padronizada cor-
respondente à tensão secundária nominal que está indicada na placa de identifica¸cão do
TC:
Z = (Rr + 2rm)2
+ (Xr)2
Exemplo: a impedância máxima (incluindo a resistência dos condutores) a ser imposta
ao secundário de um TC de prote¸cão é da ordem de grandeza de 2, 75Ω. Então, este TC
seria especificado na “ordem de compra”como A400 ou B400.
3.4.18 Resumo das Caracter´ısticas dos TCs
1. Corrente secundária: de modo geral a corrente nominal secundária é de 5A. Em casos
especiais, em prote¸cão pode haver TCs com corrente secundária nominal de 2, 5A.
2. Corrente primária: caracteriza o valor nominal de I1 suportável pelo TC. Na escolha
de um TC deve-se especificá-lo tendo em vista a corrente máximo do circuito em
que o TC vai ser inserido.
3. Classe de exatidão: valor máximo do erro, expresso em percentagem, que poderá ser
introduzido pelo TC na indica¸cão de um watt´ımetro, ou no registro de um medidor
de energia elétrica, em condi¸cões especificadas. Pode ter os valores: 0, 3, 0, 6 e 1, 2.
4. Carga nominal: carga na qual se baseiam os requisitos de exatidão do TC.
5. Fator térmico: fator pelo qual deve ser multiplicada a corrente primária nominal
para se obter a corrente primária nominal para se obter a corrente primária máxima
que um TC é capaz de conduzir em regime permanente, sob freqüência nominal,
sem exceder os limites de eleva¸cão de temperatura especificados e sem cair fora
da sua classe de exatidão. Os limites de eleva¸cão de temperatura levam em consi-
dera¸cão os diferentes tipos de materiais isolantes que podem ser utilizados nos TCs.
Especificam-se cinco fatores térmicos para TCs fabricados no Brasil: 1, 0; 1, 2; 1, 3;
1, 4; 1, 4; 1, 5 e 2, 0. Já existem em outros pa´ıses TCs de fator térmico 4, 0. Se o
usuário desejar fator térmico maior que 1, 0 em TCs nacionais, deverá explicitá-lo
na sua especifica¸cão de compra. Os fabricantes garantem que, acima da corrente
nominal, o TC até que apresentam melhor exatidão, pois nestas condi¸cões a corrente
de excita¸cão será muito pequena diante da corrente primária.
6. N´ıvel de isolamento: define a especifica¸cão do TC quanto às condi¸cões a que deve
satisfazer a sua isola¸cão em termos de tensão suportável. A padroniza¸cão das tensões
máximas de opera¸cão dos TCs (tabela abaixo), como também os correspondentes
tipos e n´ıveis de tensões a que devem ser submetidos por ocasião dos ensaios definem
desta maneira, a “tensão máxima de opera¸cão de um equipamento”: máxima tensão
de linha (tensão entre fases) para o qual o equipamento é projetado, considerando-
se principalmente a sua isola¸cão, bem como outras caracter´ısticas que podem ser

referidas a essa tensão, na especifica¸cão do equipamento considerado. Em caso de
corrente alternada é sempre dada em valor eficaz. Essa tensão não é necessariamente
igual à tensão máxima de opera¸cão do sistema ao qual o equipamento está ligado.
Tensões Máximas de Opera¸cão dos TCs (kV )
0, 6 25, 8 92, 4 362
1, 2 38 145 460
7, 2 48, 3 169 550
12 72, 5 242 765
15
Em termos práticos, na especifica¸cão de um TC, a sua tensão máxima de opera¸cão
pode ser considerada como sendo a que consta do quadro (mostrado anteriormente)
imediatamente superior à tensão nominal entre fases do circuito em que o TC será
utilizado.
7. Corrente térmica nominal: maior corrente primária que um TC é capaz de suportar
durante um segundo, com o enrolamento secundário curto-circuitado, sem exceder,
em qualquer enrolamento, uma temperatura máxima especificada. Somente há in-
teresse em se falar em corrente térmica para TCs a partir do n´ıvel de isolamento
correspondente à tensão nominal de 69kV . Como referência, podemos dizer que a
corrente térmica é no m´ınimo 75 vezes e 45 vezes a corrente primária nominal para os
TCs imersos em óleo mineral isolante e para os isolados em epoxy, respectivamente.
A corrente térmica tem também o nome de corrente de curta dura¸cão.
8. Corrente dinâmica nominal: valor de crista da corrente primária que um TC é capaz
de suportar, durante o primeiro meio ciclo, com o enrolamento secundário curto-
circuitado, sem danos elétricos ou mecânicos resultantes das for¸cas eletromagnéticas.
A norma estabelece que o valor de crista é normalmente 2, 5 vezes o valor da corrente
térmica.
9. Polaridade: Num transformador (figura abaixo) diz-se que o terminal S1 do secundário
tem a mesma polaridade do terminal P1 do primário se, quando a corrente I1 percorre
o enrolamento primário de P1 para P2, no mesmo instante a corrente I2 percorre
o instrumento A de S1 para S2. Conseqüentemente, diz-se também que S2 tem a
mesma polaridade de P2.
Quando o TC alimenta somente amper´ımetros, relés de corrente, etc., a sua po-
laridade não precisa ser levada em considera¸cão. Mas, quando ele alimenta ins-
trumentos elétricos cuja bobina de corrente é provida de polaridade relativa, como
watt´ımetros, medidores de energia elétrica, fas´ımetros, etc., então é extremamente

importante a considera¸cão da polaridade do TC: a entrada da bobina de corrente
destes instrumentos deve ser ligada ao terminal secundário do TC que corresponde
ao seu terminal primário que está ligado como entrada ao circuito principal.
Exemplo: Na figura acima, se o primário do TC for ligado em série com a carga
de modo que P1 seja entrada, isto é, P1 esteja ligado no lado da fonte e P2 no
lado da carga, então a entrada das bobinas de corrente dos instrumentos será ligada
ao terminal S1 do secundário. Da mesma forma, se P2 for ligado for ligado como
entrada, isto é P2 no lado da fonte e P1 no lado da carga, então S2 é que será
utilizado como entrada das bobinas de corrente daqueles instrumentos elétricos.
Normalmente, os terminais dos enrolamentos primário e secundário dos TCs são
dispostos de tal forma que os terminais de mesma polaridade ficam adjacentes,
como mostra a figura à esquerda acima, e não em diagonal como mostra a figura à
direita acima.
10. Se um TC alimenta vários instrumentos elétricos, Ester devem ser ligados em série a
fim de que todos eles sejam percorridos pela mesma corrente do secundário do TC.
11. Quando se empregam TCs em medi¸cão de energia elétrica para fins de faturamento
a consumidor, é recomendável que estes TCs sejam utilizados exclusivamente para
alimentar o medidor ou medidores de energia elétrica da instala¸cão. Não deve ser
permitida a coloca¸cão de outros instrumentos elétricos no secundário destes TCs,
tais como amper´ımetros, bobina de corrente de watt´ımetros, etc.
12. Damos a seguir uma ordem de grandeza para os TCs para medi¸cão:
a. n1I1 = 500 a 1000 ampéres-espiras para I1 nominal;
b. n1I0 < 1% de n1I1, para I1 nominal;
c. densidade de fluxo: B ≤ 1000 linhas/cm2
(1000 Gauss ou 0, 1 tesla);
d. comprimento médio do circuito magnético: 40cm;
e. densidade de corrente: de 1A até 2A por mm2
;
f. r2 = 0, 5Ω; 2 = 15mH.
3.5 Algumas Considera¸cões Sobre TPs e TCs
1. Os TPs e TCs servem também como elementos de isolamento entre os instrumentos
ligados no secundário e o circuito de alta tensão, reduzindo assim o perigo para
o operador e tornando desnecessária uma isola¸cão especial para tais instrumentos.
Assim, é que há TCs de 5/5A, mas com n´ıvel de isolamento para alta tensão.
2. Um mesmo instrumento elétrico, utilizado com TCs e TPs de diferentes rela¸cões
nominais, pode servir para um campo muito largo de medi¸cões gra¸cas à padroniza¸cão
dos valores secundários deles (5A para os TCs e 115V para os TPs).
3. Deve-se ter o cuidado de ligar à terra o secundário e o núcleo dos TCs e TPs por
medida de seguran¸ca. Além disso, os TCs para alta tensão (a partir de 69kV ) são

constru´ıdos normalmente com camadas de material condutor (blindagem) envol-
vendo o enrolamento primário para uniformiza¸cão da distribui¸cão dos potenciais.
Estas camadas são ligadas entre si e também a um terminal externo, o qual deve
ser ligado à terra.
4. Os TCs e TPs têm todos os terminais primários e secundários providos de marcas
indeléveis. Estas marcas permitem ao instalador a rápida identifica¸cão dos terminais
de mesma polaridade. O instalador somente precisa se preocupar com a polaridade
no momento em que for ligar ao secundário dos TCs ou TPs os instrumentos elétricos
que têm bobinas providas de polaridade relativa: watt´ımetros, medidores de energia
elétrica, fas´ımetros, etc. A entrada das bobinas destes instrumentos deve ser ligada
ao terminal secundário do TC ou TP que corresponde ao terminal primário que foi
utilizado como entrada.
5. É aconselhável, antes de instalar os TCs e TPs, verificar pelo menos a rela¸cão de
transforma¸cão nominal e a polaridade. A figura abaixo mostra uma montagem sim-
ples para verificar a polaridade: a resistência R será ajustada de modo a limitar a
corrente no milivolt´ımetro mV ; a pilha pode ser de apenas 3V ; ao fechar o inter-
ruptor K, se o ponteiro do milivolt´ımetro desviar para o positivo, então o terminal
marcado P do primário corresponde ao terminal marcado S no secundário; observar
a maneira correta de ligar os pólos positivo e negativo da pilha e do milivolt´ımetro,
conforme está na figura.
6. O núcleo dos TPs e TCs é feito de chapas de ferro-sil´ıcio. Para os de melhor qualidade,
emprega-se ferro-sil´ıcio de grãos orientados, laminado a frio, conseguindo-se bons
resultados quanto à permeabilidade magnética e menores perdas. Os TCs especiais,
os que serão utilizados como padrão, por exemplo, para os quais se exige excelente
classe de exatidão, têm o núcleo feito de chapas de ligas especiais de ferro-n´ıquel.
Estas ligas têm alta permeabilidade magnética e perdas reduzidas, mas o seu custo é
bem maior que o custo dos núcleos de ferro-sil´ıcio usuais. Como exemplo, citaremos
algumas destas ligas:
6.1. FERRO-MU ou MUMETAL: 77% de n´ıquel, 5% de cobre, 2% de cromo e 16%
de ferro. Para uma mesma densidade de fluxo, a corrente de excita¸cão para
esta liga é cerca de 1/4 da corrente de excita¸cão para a liga de ferro-sil´ıcio.

Entretanto, o pre¸co de um núcleo de MUMETAL é cerca de 5 a 6 vezes o pre¸co
de um núcleo de ferro-sil´ıcio.
6.2. PERMANDUR: 49% de ferro, 49% de cobalto e 2% de vanádio.
6.3. MONIMAX: 47% de n´ıquel, 3% de molibdênio e 50% de ferro.
3.6 Emprego para os Transformadores de Instrumen-
tos na Medi¸cão de Potência Ativa e Reativa
No caso de tensão elevada e corrente intensa, superiores à tensão e à corrente su-
portáveis pelas bobinas Bp e Bc, respectivamente, faz-se necessário o emprego dos trans-
formadores para instrumentos, TPs e TCs. Há casos na prática em que a tensão da linha
é suportável por Bp e, portanto, empregam-se apenas os TCs.
Duas precau¸cões devemos tomar em rela¸cão aos transformadores para instrumentos:
observar a polaridade e aterrar o secundário e o núcleo.
3.6.1 Método dos Três Watt´ımetros para Potência Ativa com
TPs e TCs
A Figura abaixo esquematiza a montagem a realizar. Sendo Kc a rela¸cão nominal dos
TCs e Kp a rela¸cão nominal dos TPs, temos que a potência ativa total P solicitada pela
carga Z será:
P = KcKp (W1 + W2 + W3)
3.6.2 Método dos Dois Watt´ımetros para Potência Ativa com
TPs e TCs
A Figura abaixo esquematiza a montagem a realizar. Observamos que os transforma-
dores apenas são intercalados entre o circuito e os watt´ımetros, não alterando o princ´ıpio
da liga¸cão dos dois watt´ımetros quando empregados sem transformadores. A potência
total P:
P = KcKp (W1 + W2)

3.6.3 Método dos Dois Watt´ımetros para Potência Reativa com
TPs e TCs
A montagem está indicada na Figura abaixo. A potência reativa total Q será:
Q = KcKp
(W1 + W2)
2
·
√
3
3.6.4 Cálculo do Erro Introduzido pelos TPs e TCs na Indica¸cão
do Watt´ımetro
Suponhamos uma carga Z, de fator de potência indutivo cosθ submetida à tensão U1
e percorrida pela corrente I1, como na Figura abaixo.
A potência ativa exata da carga será:
P = U1I1 cos θ
Os transformadores introduzem erros de fase, respectivamente iguais a γ e β, e o
watt´ımetro W dará a seguinte indica¸cão levando em conta a Figura abaixo:
W = U2I2 cos θ

O valor medido da potência ativa será então:
P = KcKpW ou
P = KpKcU2I2 cos θ
Dividindo membro a membro as expressões acima:
P
P
=
U1I1 cos θ
KpU2KcI2 cos θ
Como U1 = FCRp · KpU2 e I1 = FCRc · KcI2, temos que:
P = P · FCRpFCRc ·
cos θ
cos θ
Exemplo Numérico
1. TC: 30/5A:
Kc = 6; FCRc = 0, 998; β = 10
2. TP: 13800/115V :
Kp = 120; FCRp = 0, 996; γ = −12
3. Indica¸cão do watt´ımetro: W = 300W
4. Valores lidos: U2 = 115V e I2 = 4A
Dos valores acima vê-se que:
P = 300 · 6 · 120 = 216000W
cosθ =
300
4 · 115
= 0, 652 ∴ θ = 49o
29
Da Figura acima vê-se que:
θ = 49o
29 + 10 + 12 = 49o
51 ∴ cos θ = 0, 649
E então a potência ativa exata P será:
P = 216000 · 0, 998 · 0, 996 ·
0, 649
0, 652
P = 213717W

3.7 Emprego para os Transformadores de Instrumen-
tos no Controle e Supervisão
Os instrumentos de controle e supervisão mostrados nesta sessão foram utilizados
na prática e foram instalados pela TRANSNOR - Transformadores do Nordeste S.A. -
durante os meses de Agosto e Janeiro de 2006/2007.
3.7.1 Módulo 5520 Deep Sea Eletronics
O modelo 5520 é um módulo para controle automático de falha da rede. O módulo é
usado para monitorar a rede e automaticamente partir um gerador em espera. E quando
na presen¸ca de falhas, automaticamente desligando o gerador e indicando as mesmas por
meio do display. Com o 5520 pode-se ainda programar entradas do gerador em horas
predeterminadas, por exemplo, em horários de pico para diminuir a demanda de carga da
rede, e assim, diminuir um poss´ıvel excesso na demanda contratada com o fornecedor de
energia elétrica. Através de um computador e um software fornecido, pode-se monitorar
a opera¸cão do sistema localmente, ou remotamente. O acesso ao modulo é protegido por
um número PIN para prevenir acessos não autorizados. A opera¸cão do módulo é feita
através de botões de controle localizados no painel, onde poderá se realizar as fun¸cões
como parar a máquina, ligar, etc.
Este módulo foi montado para operar no controle de um grupo gerador no hotel
Pirâmide, localizado na Via Costeira em Natal. O mesmo deve não só monitorar a rede
para entrar em um caso de falha, como também entrar no horário de pico de tarifa¸cão
da energia para diminuir o consumo. O mesmo entra sincronizado com a rede e a sua
entrada é quase impercept´ıvel aos usuários. O gerador supre a carga em paralelo com a
rede, visto que o mesmo não possui a potência total necessária para substitu´ı-la.
O mesmo utiliza de TPs e TCs para medi¸cão de tensão e corrente da sa´ıda do grupo
gerador. Para a configura¸cão dos transformadores de instrumentos utilizados no módulo,
são inseridas além da rela¸cão nominal Kp, os fatores de corre¸cão de rela¸cão FCRp e FCRc
do TP e do TC, respectivamente, calculando-se a rela¸cão real Kr para a medi¸cão correta.

3.7.2 Módulo 5510 Deep Sea Eletronics
O modelo 5510 é um modulo para controle de máquinas elétricas automático. O
módulo é usado para automaticamente acionar e parar a máquina, indicando as suas
caracter´ısticas de opera¸cão e condi¸cões de falta por meio de um display lcd e leds indica-
dores no painel. Seqüências de opera¸cão, temporizadores e alarmes podem ser alterados
pelo usuário. Através de um computador e um software fornecido, pode-se monitorar a
opera¸cão do sistema localmente, ou remotamente. O acesso ao modulo é protegido por
um número PIN para prevenir acessos não autorizados. O 5510 tem a capacidade de
sincroniza¸cão e divisão de carga. O módulo 5510 possui sa´ıdas flex´ıveis que permitem a
conexão aos mais comuns reguladores automáticos de tensão e controladores de veloci-
dade. A opera¸cão do módulo é feita através de botões de controle localizados no painel,
onde poderá se realizar as fun¸cões como parar a máquina, ligar, etc.
O mesmo utiliza de TPs e TCs para medi¸cão de tensão e corrente da sa´ıda da máquina.
Para a configura¸cão dos transformadores de instrumentos utilizados no módulo, são in-
seridas além da rela¸cão nominal Kp, os fatores de corre¸cão de rela¸cão FCRp e FCRc do
TP e do TC, respectivamente, calculando-se a rela¸cão real Kr para a medi¸cão correta.
A instala¸cão deste módulo foi requisitada pela Petrobrás para operar em plataforma.
Devido a isto, uma caracter´ıstica foi frisada quanto a liga¸cão do mesmo: a eletricidade na
plataforma trabalha com 3 fases - 3 fios, ou seja, com terra flutuante. Esta caracter´ıstica
impossibilitou a utiliza¸cão de TPs para leitura de tensão, o motivo foi de uma configura¸cão
do módulo que não poderia ser alterada.
3.7.3 Multitransdutor Digital Kron MKM-D com Memória de
Massa
O multitransdutor digital da Kron MKM-D com Memória de Massa foi adquirido para
a montagem de um quadro para a UFPB - Universidade Federal da Para´ıba - que deveria
ler as medidas de tensão, freqüência, fator de potência, energia ativa e reativa e consumo
de energia de um grupo motor diesel convertido para gás e um gerador, devendo gravar
estes dados para análise na memória de massa. A montagem faz parte de um projeto
de Engenharia Mecânica para o estudo do gás natural como combust´ıvel alternativo. A
carga do gerador é composta de um banco de resistência.

O mesmo pode utilizar de TPs e TCs para medi¸cão de tensão e corrente. Para a
configura¸cão dos transformadores de instrumentos utilizados no módulo, são inseridas
além da rela¸cão nominal Kp, os fatores de corre¸cão de rela¸cão FCRp e FCRc do TP e do
TC, respectivamente, calculando-se a rela¸cão real Kr para a medi¸cão correta.

Medidas eletricas prof_marcus_vinicius

Mais conteúdo relacionado

Mais procurados

Semelhante a Medidas eletricas prof_marcus_vinicius

Medidas eletricas prof_marcus_vinicius