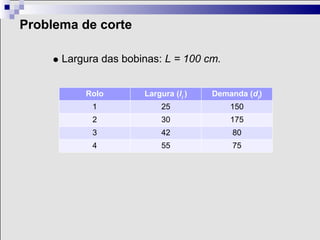
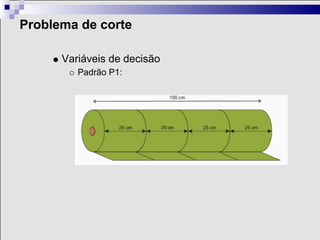
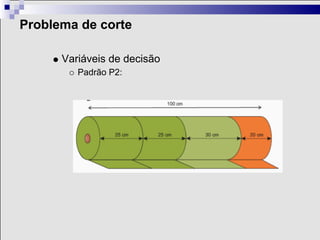
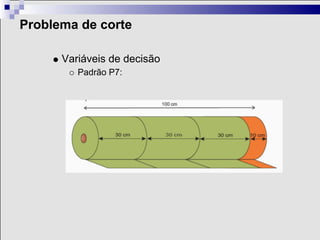
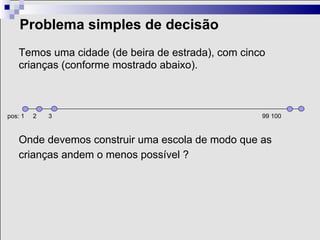
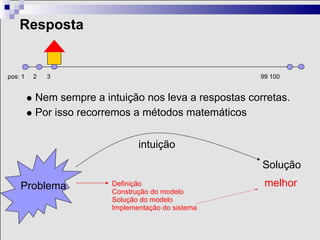
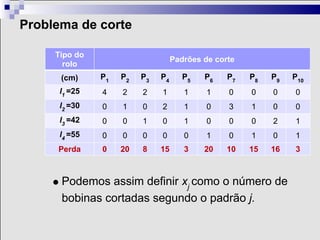
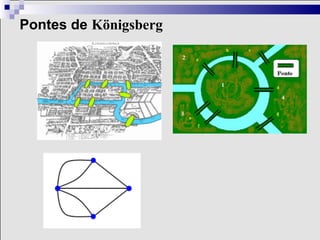
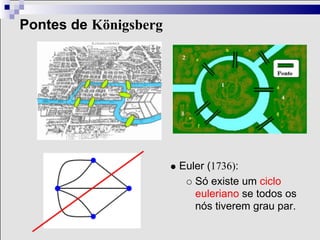
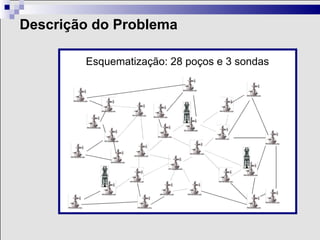
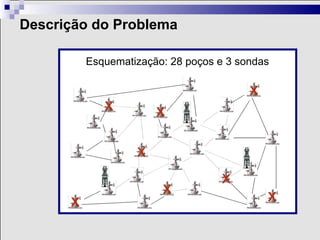
1) A otimização é um ramo matemático que ajuda na tomada de decisões complexas em diversos contextos, como logística, finanças e indústria. 2) Problemas de otimização envolvem definir variáveis de decisão, uma função objetivo e restrições para encontrar a melhor solução. 3) A otimização tem aplicações históricas e é amplamente usada na indústria, por exemplo, para planejar rotas eficientes de sondas em uma bacia de petróleo.

1. Introdução à Otimização
e sua aplicação na Indústria.

2. Tomada de decisões
Em uma estrada: Qual o melhor caminho a tomar?
Na bolsa de valores: Em que companhias investir?
Em uma indústria: O que e em que ordem produzir?
Em um trabalho em grupo: Que pessoas alocar a
que tarefas ?
Em uma prestadora de serviço: Quais clientes a
tender e em que momento?
No governo: Onde construir uma escola ou hospital?
Em geral, as decisões são baseadas em
experiências anteriores intuição.

3. Problema simples de decisão
Temos uma cidade (de beira de estrada), com cinco
crianças (conforme mostrado abaixo).
pos: 1 2 3 99 100
Onde devemos construir uma escola de modo que as
crianças andem o menos possível ?

4. Resposta
pos: 1 2 3 99 100
Nem sempre a intuição nos leva a respostas corretas.
Por isso recorremos a métodos matemáticos
intuição
Solução
Problema Definição melhor
Construção do modelo
Solução do modelo
Implementação do sistema

5. Ainda sobre o problema da escola
Note que existe mais de uma maneira de se olhar para
o mesmo problema.
pos: 1 2 3 99 100
Função objetivo:
Minimizar a soma do que todas as crianças andam.
Minimizar a quantidade caminhada pela criança que mais
anda.
Minimizar as diferenças entre as quantidades caminhadas
pelas crianças.
Minimizar o número de crianças que andam mais que uma
certa distância.
Combinações de objetivos (!)

6. Otimização
Ramo interdisciplinar da matemática aplicada que faz
uso de modelos matemáticos, estatísticos e de
algoritmos na ajuda à tomada de decisões.
Em um problema de otimização temos uma função
objetivo e um conjunto de restrições, ambos relacionados
às variáveis de decisão.
O problema pode ser de minimização ou de maximização da
função objetivo.
Procura-se encontrar o menor (ou maior) valor possível para
a função objetivo para o qual o valor atribuído às variáveis
não viole nenhuma restrição.

7. Pontes de Königsberg

8. Pontes de Königsberg
Euler (1736):
Só existe um ciclo
euleriano se todos os
nós tiverem grau par.

9. II Guerra Mundial
Problema: Tamanho dos comboios!
O que é melhor usar ?
a) vários comboios pequenos (mais rápidos)
b) poucos comboios grandes (mais protegidos)

10. Muito além dos fins militares...

11. Exemplo - Problema de corte
O problema consiste a cortar bobinas de
papel de largura L em rolos de largura li
(onde i = 1, . . . ,m) a fim de satisfazer uma
demande di .

12. Problema de corte
Largura das bobinas: L = 100 cm.
Rolo Largura (li ) Demanda (di)
1 25 150
2 30 175
3 42 80
4 55 75

13. Problema de corte
Variáveis de decisão
Neste problema, é preciso primeiro identificar os
diferentes padrões de corte reallizados pela máquina de
corte.

14. Problema de corte
Variáveis de decisão
Padrão P1:

15. Problema de corte
Variáveis de decisão
Padrão P2:

16. Problema de corte
Variáveis de decisão
Padrão P7:

17. Problema de corte
Tipo do
Padrões de corte
rolo
(cm) P1 P2 P3 P4 P5 P6 P7 P8 P9 P10
l1 =25 4 2 2 1 1 1 0 0 0 0
l2 =30 0 1 0 2 1 0 3 1 0 0
l3 =42 0 0 1 0 1 0 0 0 2 1
l4 =55 0 0 0 0 0 1 0 1 0 1
Perda 0 20 8 15 3 20 10 15 16 3
Podemos assim definir xj como o número de
bobinas cortadas segundo o padrão j.

18. Problema de corte

19. Problema de Linha Automotiva
O trabalho de programação da produção das fábricas de carros
consiste em:
1. Determinar o dia de produção para cada carro, de acordo
com as capacidades da linha de produção e datas de
entrega;
2. Escalonar a ordem dos carros a serem produzidos em cada
dia de produção, satisfazendo os requisitos de atelier de
carroceria, atelier de pintura e atelier de montagem.

20. Problema de Linha Automotiva
Requisitos de pintura
Deve-se minimizar o consumo de solvente de tinta,
usado para lavar as pistolas de spray nas mudanças
de cores de tinta entre carros consecutivos.
Portanto, existe o requisito de escalonar
consecutivamente carros de mesma cor.
Minimizar o número de trocas de cor de tinta (lavagens)
na seqüência de carros escalonados, ou seja,
escalonar os maiores grupos de cores possíveis.

21. Problema de Linha Automotiva
Requisitos de linha de montagem:
Carros podem requerer operações adicionais de
montagem, associadas a opções especiais.
Estes carros não devem exceder um certa quota
sobre qualquer seqüência de carros, ou seja, devem
ser distribuídos igualmente ao longo do dia de
produção.

22. Problema de Linha Automotiva
ROADEF Challenge
ROADEF é a Sociedade Francesa de Pesquisa Operacional e
Apoio à Decisão.
ROADEF lança concursos a cada dois anos.
O problema apresentado para o Challenge ROADEF 2005 foi
proposto pela Renault.
Nossa equipe ficou em 2º. lugar numa competição envolvendo
55 equipes de 15 países.

23. Bacia petrolífera potiguar
2% poços surgentes
98% usam métodos artificiais de elevação

24. Sondas de Produção Terrestre
Sondas de Produção Terrestre - SPT
São unidades móveis que realizam serviços de intervenção em poços, com
o objetivo de manter a produção ou aumentar sua produtividade.
Principais causas:
Falhas mecânicas;
Excesso de gás;
Excesso de água;
Produção de areia.
Transporte das SPT
SPT Montada

25. Descrição do Problema
Esquematização: 28 poços e 3 sondas

26. Descrição do Problema
Esquematização: 28 poços e 3 sondas
x
x x
x
x
x x
x

27. Descrição do Problema
A decisão de qual sonda encaminhar a uma
determinada solicitação de serviço depende de
fatores como:
Potencial produtivo do poço (vazão m3/dia)
Localização geográfica da sonda em relação ao poço
Tempo de intervenção no poço
Questões de risco ambiental e segurança
Limitação técnica da sonda em relação a profundidade do
poço
Como o custo operacional das sondas é alto, tal
processo deve ser otimizado.

28. Resultados do projeto
Solução:
Construção de rotas para as sondas de produção
terrestre.
Sistema implementado na Petrobras.
Ganhos médios de produção de 425m3 a
cada 15 dias comparado à solução anterior
da Petrobras.

29. Introdução à Otimização
e sua aplicação na Indústria.