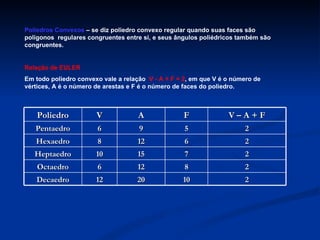
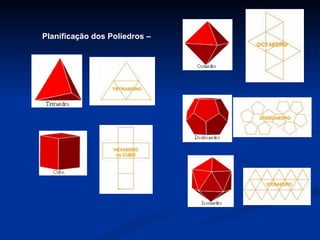
O documento discute Platão e sua filosofia, poliedros geométricos, e compara estruturas moleculares com formas geométricas. Ele fornece detalhes biográficos sobre Platão e sua Academia, define características de poliedros como faces, arestas e vértices, e usa exemplos como o hexafluoreto de enxofre para ilustrar semelhanças entre moléculas e formas geométricas.

1. Sólido Geométricos Poliedros

5. Vejamos alguns exemplos de poliedros: 6 faces 8 vértices 12 arestas Cubo 4 faces 4 vértices 6 arestas Tetraedro 8 faces 6vértices 12 arestas Octaedro

6. Poliedros Convexos – se diz poliedro convexo regular quando suas faces são polígonos regulares congruentes entre si, e seus ângulos poliédricos também são congruentes. Relação de EULER Em todo poliedro convexo vale a relação V - A + F = 2 , em que V é o número de vértices, A é o número de arestas e F é o número de faces do poliedro. Poliedro V A F V – A + F Pentaedro 6 9 5 2 Hexaedro 8 12 6 2 Heptaedro 10 15 7 2 Octaedro 6 12 8 2 Decaedro 12 20 10 2

8. Exemplos de formas de poliedros

9. Planificação dos Poliedros –

12. Referencias bibliográficas : BONJORNO & GIOVANNI – Matemática Completa – 2 ª Série – Editora FTD – 2005 PAIVA, MANOEL – Matemática – Volume Único – Editora Moderna – 1999 LAPA, NILTON e CAVALLANTE,SIDNEY LUIZ – Matemática – Editora Moderna – 1987. DANTE, LUIZ ROBERTO – Matemática Contexto & Aplicações – Editora`Ática – 1999 SMOLE, KÁTIA STOCCO & DINIZ, MARIA IGNEZ – Matemática – Ensino Médio – Edira Saraiva – 2009. FILHO,BENIGNO BARRETO & SILVA , CLAÚDIO XAVIER DA – Matemática Aula por Aula – 2ª série – Editora FTD – 2003. Vídeo : http://www.youtube.com/watch?v=6CTo4HLHQVw http://www.youtube.com/watch?v=gBQLVgRTesg&feature=related

13. Trabalho sobre os Poliedros de Platão Curso Pós Graduação - Novas Tecnologias no Ensino da Matemática – UFF Lante Informática Educativa II Aluno: Márcia Luzia D. Gama