- A trigonometria surgiu na Grécia antiga para medir triângulos, mas seu desenvolvimento como ciência se deu principalmente a partir do trabalho de astrônomos como Hiparco de Nicéia, que introduziu tabelas trigonométricas.
- Matemáticos indianos e árabes deram novos avanços à trigonometria, como a introdução da trigonometria esférica e a elaboração de fórmulas fundamentais.
- A trigonometria consolidou-se como ciência autônoma a


















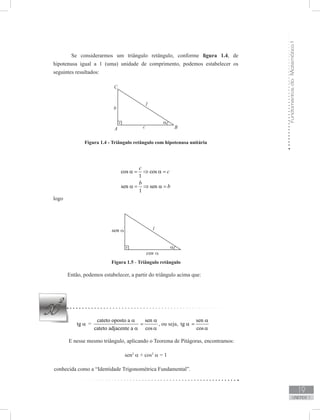



































![FundamentosdaMatemáticaI
57
unidade 2
Utilizando os dados da tabela abaixo, a representação gráfica da função seno
é dada pela figura 2.25:
x sen x
0 0
π/6 0,5
π/3 0,866
π/2 1
2π/3 0,866
5π/6 0,5
π 0
7π/6 -0,5
4π/3 -0,866
3π/2 -1
5π/3 -0,866
11π/6 -0,5
2π 0
Figura 2.25 - Gráfico da função seno – senóide
Observando o gráfico da figura 2.25, podemos concluir que:
I- Como é possível determinar o sen x, para todo arco de medida x ∈ R, então o
domínio da função seno é o conjunto dos números reais.
II- Como o raio do ciclo trigonométrico é 1, então a imagem da função seno é o
intervalo fechado [−1,1], isto é, −1 ≤ sen x ≤ 1.
III- A função seno é periódica de período 2π, pois sen (x+2π) = sen x.
IV- A função seno tem intervalos de crescimento e decrescimento.](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-57-320.jpg)

![FundamentosdaMatemáticaI
59
unidade 2
Observando o gráfico da figura 2.26, podemos concluir que:
I- Como para todo arco de medida x ∈ R é possível determinar o cos x, então o
domínio da função cosseno é o conjunto dos números reais.
II- Como o raio do ciclo trigonométrico é 1, então a imagem da função cosseno é o
intervalo fechado [−1,1], isto é − 1 ≤ cos x ≤ 1.
III- A função cosseno é periódica de período 2π, pois cos (x+2π) = cos x.
IV- A função cosseno tem intervalos de crescimento e decrescimento.
Uma importante característica da função seno e da função cosseno está
relacionada com a paridade. Para todos os números reais vale, conforme você já
estudou:
Figura 2.27 - Simetrias do seno e cosseno
sen α = − sen (− α) e cos α = cos (− α)
Lembre-se de que
uma função f(x) é
par se, para todo
x no seu domínio,
tivermos f(x) =
f(−x). Uma função
é ímpar se, para
todo x no seu
domínio, tivermos
f(x) = − f(−x).
De acordo com essas igualdades, podemos afirmar que a função seno é uma
função ímpar, e a função cosseno é uma função par.](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-59-320.jpg)




![UniversidadeAbertadoBrasil
64
unidade 2
2.4.5 Função secante
Definimos a secante como sendo a relação expressa por:
1
sec
cos
x
x
= .
Como a relação apresenta um cosseno no denominador, temos que assegurar
que esse cosseno nunca seja zero, pois não é permitida a divisão por zero. Você
estudou que o cosseno é zero apenas nos ângulos da forma kπ+
2
π
, com k ∈ Z.
Assim, podemos dizer que o domínio da função secante é definido em todos os reais,
exceto nos ângulos que zeram o cosseno.
Dado um ângulo, cuja medida em radianos é x, chamamos de função secante,
a função que associa a cada x ,
2
k k z
π
≠ + π ∈ o número sec x ∈ R e indicamos
por:
f(x) = sec x
onde sec x =
1
cos x
; cos x ≠ 0, ou seja, x ,
2
k k Z
π
≠ + π ∈ .
Graficamente temos:
Figura 2.31 - Gráfico da função secante
Observando o gráfico da figura 2.31, podemos concluir que:
I. Como para todos os valores de x = kπ +
2
π
, com k ∈ Z a secante não está
definida, então o domínio da função secante é o conjunto
{x ∈ R | x ,
2
k k z
π
≠ + π ∈ }.
II. A imagem da função secante é o conjunto R − ]−1,1[.
III. A função secante é periódica de período 2π, pois sec (x+2π) = sec x.
IV. A função secante é par, pois é proporcional ao inverso do cosseno, que é uma
função par.
,
2
k k Z
π
≠ + π ∈
,
2
k k Z
π
≠ + π ∈](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-64-320.jpg)

![UniversidadeAbertadoBrasil
66
unidade 2
Graficamente teremos
Figura 2.32 - Gráfico da função cossecante
Observando o gráfico da figura 2.32, podemos concluir que:
I. Como para todos os valores de x = kπ, com k Z∈ a cossecante não está definida,
então o domínio da função cossecante é o conjunto {x ∈ R | pkx ≠ , k ∈ Z}.
II. A imagem da função cossecante é o conjunto R−]−1,1[.
III. A função cossecante é periódica de período 2π, pois cossec (x + 2π) = cossec x.
IV. A função cossecante é uma função ímpar, pois é proporcional ao inverso do seno,
que é uma função ímpar.
ATIVIDADE COMPUTACIONAL
No Graphmat, desenvolva as atividades a seguir. Faça suas conclusões
referentes a cada tipo de função envolvida em relação ao domínio, imagem e período,
tendo sempre como pano de fundo o gráfico da figura 2.32.
Faça o gráfico da função y = cossec x (função mãe) e, a partir dele, analise
as situações a seguir:
a) y = a⋅cossec x, onde “a” é um número real;
b) y = b + a⋅cossec x, mantendo “a” constante e variando “b”;
c) y = cossec (x + a), onde “a” é um número real;
d) y = cossec (ax), onde “a” é um número real;
e) y = c + d⋅cossec (ax + b), onde “a”, “b”, “c” e “d” são números reais.
π](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-66-320.jpg)



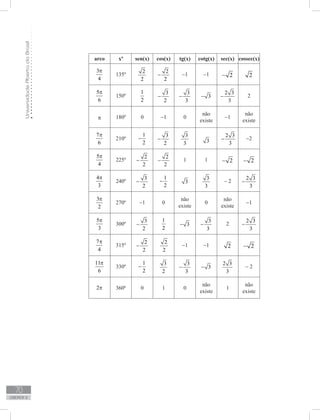


![FundamentosdaMatemáticaI
73
unidade 2
para um valor de y correspondem infinitos valores de x. Se y = 0, sen x = 0, podemos
tomar x = 0, x = 2π, x = 4π, x = −2π, etc., isto é, x = 2k π, onde k é um número inteiro;
isso quer dizer que não podemos definir a inversa de f(x) = sen x em seu domínio.
Devemos então restringir o domínio para um subconjunto dos números reais onde a
função é bijetora.
Como as funções trigonométricas são periódicas, existem muitos intervalos
em que elas são bijetoras. É usual escolher como domínio intervalos onde o zero é o
ponto médio ou o extremo esquerdo e no qual a função percorra todo seu conjunto
imagem.
Vamos ver como devemos definir a função arco-seno.
3.2 Função arco-seno
Considerando a função f(x) = sen x, vamos redefinir o seu domínio no intervalo
,
2 2
π π
−
e imagem no intervalo [−1,1].Afunção inversa de f(x) = sen x, denominada
função arco seno, definida por 1
f −
: [−1, 1] → ,
2 2
π π
−
, é denotada por
1
f −
(x) = arc sen x.
Assim y = arc sen x ⇔ sen y = x.
Gráfico das funções seno e arco-seno :
Figura 2.35 - Gráfico da função seno e da função arco-seno
Observe o gráfico da função arco-seno, na figura 2.35, para identificar as
seguintes características:
O domínio da função é [• −1, 1];
A imagem da função é• ,
2 2
π π
−
;
A função é sempre crescente.•](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-73-320.jpg)
![UniversidadeAbertadoBrasil
74
unidade 2
Figura 2.36 - Gráfico da função arco-cosseno
Observando o gráfico da função arco-cosseno, na figura 2.36, podemos
identificar as seguintes características:
O domínio da função é [• −1, 1];
A imagem da função é [0,• p] ;
A função é sempre decrescente.•
3.4 Função arco-tangente
Dada a função f(x) = tg x, com domínio restrito ,
2 2
π π
−
e imagem em R,
a função inversa de f, denominada função arco tangente, é definida por
1
f −
: R → ,
2 2
π π
−
e denotada por 1
f −
(x) = arc tg x.
3.3 Função arco-cosseno
Seja a função g(x) = cos x, com domínio restrito [0,p] e imagem [−1,1]. A
função inversa de g, denominada função arco cosseno, é definida por
1−
g : [−1, 1]→ [0,p] e denotada por 1−
g : (x) = arc cos x.
Assim y = arc cos x ⇔ cos y = x.
Gráfico da função arco-cosseno:](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-74-320.jpg)
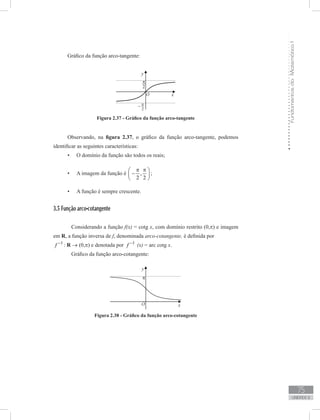
![UniversidadeAbertadoBrasil
76
unidade 2
Observando, na figura 2.38, o gráfico da função arco-cotangente, podemos
identificar as seguintes características:
O domínio da função são todos os reais;•
A imagem da função é (0,• π);
A função é sempre decrescente.•
Como exercício, tente agora você definir as funções arco-secante e arco-
cossecante e em seguida trace os seus gráficos.
Determine o valor de1) y:
a) y = arc sen
1
2
Resolução:
Usando a equivalência y = arc sen x ⇔ sen y = x temos que sen y =
1
2
.
Como y ∈ ,
2 2
π π
−
e x 0, então y =
6
π
.
b) y = arc cos
2
2
−
Resolução:
Pela definição temos que cos y =
2
2
− . Como y ∈ [0,p] e x 0, então y =
3
4
π
.
c) y = arc tg 3
Resolução:
Como tg y = 3 , y ∈ ,
2 2
π π
−
e x 0, então y =
3
π
.](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-76-320.jpg)














![FundamentosdaMatemáticaI
91
unidade 3
cos (a + b) =
OM OD ED CD
CDOD OC OC
⋅ − ⋅
Logo,
cos (a + b) = cos a . cos b − sen a . sen b
Cosseno da diferença: cos (a – b)•
Fazendo: cos (a – b) = cos [a + (–b)], aplicamos a fórmula da soma:
cos (a – b) = cos [a + (–b)] = cos a . cos (–b) – sen a . sen (–b)
Lembrando que: sen (–b) = –sen b e cos (–b) = cos b, podemos escrever:
cos (a − b) = cos a . cos b + sen a . sen b
Seno da soma: sen (a + b)•
Já estudamos que:
sen a cos a
2
cos a sen a
2
π
− =
→
π − =
arcos complementares
Então, podemos escrever:
sen(a + b) = cos (a b)
2
π
− +
sen (a + b) = cos a b
2
π
− −
sen (a + b) = cos a b
2
π
− −
Utilizando a fórmula cos (a + b) = cos a . cos b − sen a . sen b, temos:
sen (a+b) = cos a cos( b) sen a sen ( b)
2 2
π π
− ⋅ − − − ⋅ −
sen (a + b) = sen a . cos b + sen b . cos a](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-91-320.jpg)
![UniversidadeAbertadoBrasil
92
unidade 3
Seno da diferença: sen (a – b)•
Fazendo: sen (a – b) = sen [a + (–b)], aplicamos a fórmula da soma:
sen (a – b) = sen [a + (–b)] = sen a . cos (–b) + sen (–b) . cos a
Lembrando que: sen (–b) = –sen b e cos (–b) = cos b, podemos escrever:
sen (a – b) = sen a . cos b – sen b . cos a
Tangente da soma: tg (a + b)•
Como já determinamos o seno e o cosseno da soma, podemos também
obter a tangente da soma.
Sabemos que
sen (a b)
tg (a b)
cos (a b)
+
+ =
+
Aplicando as fórmulas calculadas anteriormente no 2º membro, temos:
sen a cos b sen b cos a
tg (a b)
cos a cos b sen a sen b
⋅ + ⋅
+ =
⋅ − ⋅
Dividindo o numerador e o denominador da última expressão por
“cos a . cos b”, temos:
sen a cos b sen b cos a
cos a cos b cos a cos btg (a b)
cos a cos b sen a sen b
cos a cos b cos a cos b
⋅ ⋅
+
⋅ ⋅+ =
⋅ ⋅
−
⋅ ⋅
, simplificando obtemos:
sen a sen b
cos a cos btg (a b)
sen a sen b
1
cos a cos b
+
+ =
− ⋅
Como
sen a
tg a
cos a
= e
sen b
tg b
cos b
= , temos:
tg a tg b
tg (a b)
1 tg a tg b
+
+ =
− ⋅](https://image.slidesharecdn.com/fundamentosmatematicai-200520154347/85/Fundamentos-matematica-Elementar-92-320.jpg)



































