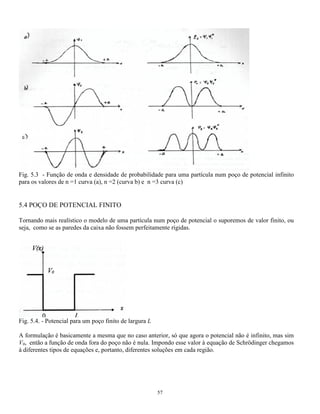
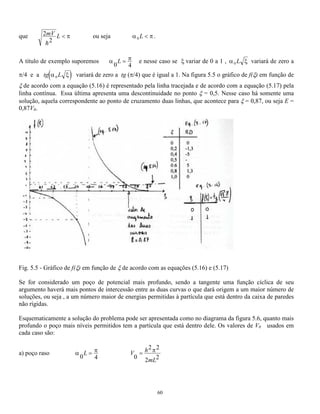
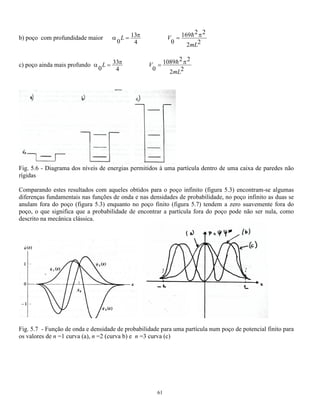
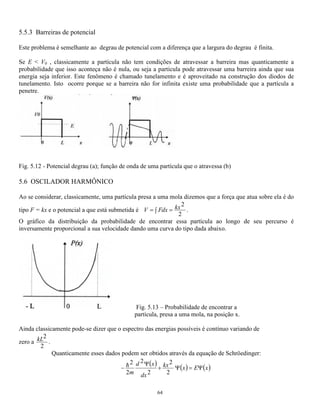
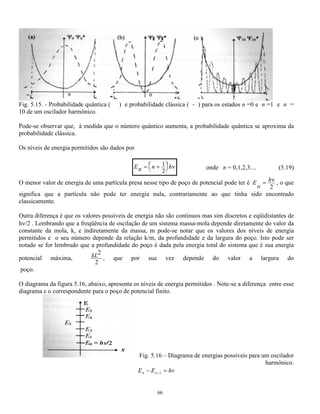
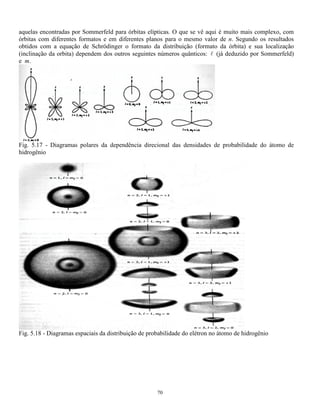
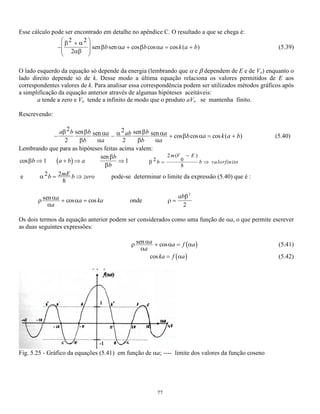
O documento resolve a equação de Schrödinger para diversos tipos de potenciais atuando sobre uma partícula, incluindo poços de potencial infinito e finito. A solução para um poço infinito mostra que a energia da partícula é quantizada em valores discretos. A solução para um poço finito é similar, mas com funções de onda não nulas fora do poço devido ao potencial finito.

1. 5 SOLUÇÃO DA EQUAÇÃO DE SCHRÖDINGER PARA DIVERSOS
PROBLEMAS
À título de ilustração a equação de Schrödinger será resolvida para diversos tipos de forças atuando sobre
uma partícula.
d
dx
52
5.1 POÇO DE POTENCIAL
Uma partícula é dita livre quando sobre ela não existe nenhuma influência, nenhuma ação. De outro modo, se
numa certa região do espaço existir um campo de forças ele influirá sobre os corpos que possuem a
propriedade suscetível à sua ação. Por exemplo o campo gravitacional atua sobre os corpos que tem massa, o
campo elétrico sobre as partículas que tem carga e o campo magnético sobre os ímãs.
A idéia do efeito, criado por um campo, pode ser melhor visualizada através da seguinte imagem: tem-se um
colchão plano horizontal, uma bolinha de gude colocada em qualquer ponto de sua superfície aí
permanecerá, se porém antes de realizar esta experiência tiver sido colocada sobre o colchão uma grande
bola de boliche, a bolinha não permanecerá no ponto em que ela for deixada mas tenderá a descer para o
buraco formado pela pesada bola. Esse exemplo evidencia a influência que um corpo, no caso a bola de
boliche, pode exercer à sua volta e portanto o campo que ele pode criar.
Um campo é considerado conservativo quando a energia da partícula presente só depende da sua posição na
região em que o campo atua, e nesse caso a energia é uma função da posição. Isso quer dizer que, ao realizar
um caminho fechado dentro do campo, a partícula volta à sua energia inicial, ou seja, ela não perde energia
num circuito fechado, daí o nome de campo conservativo.
Para os campos conservativos é definida a grandeza física “potencial”, V(r) , que é função só da posição e
que está relacionada à força que atua sobre a partícula através da seguinte expressão:
F
V r
r
= −
( )
(5.1)
Essa expressão será usada sempre que se desejar conhecer o potencial, ao qual está submetida uma partícula,
a partir da força que atua sobre ela e vice versa.
5.2 PARTÍCULA LIVRE
Partícula livre é aquela que não está submetida a nenhuma força. Fazendo F=0 na expressão (5.1) obtém-se
que V(r) deve ser constante. No nosso caso, para simplificar a solução, escolheremos essa constante igual a
zero, o que não altera as soluções do problema.
Considerando-se o movimento da partícula como unidimensional, ou seja, tendo-se somente x como variável,
as derivadas parciais transformam-se em derivadas totais. Assim, substituindo-se V = 0 na equação de
Schrödinger (4.25) obtém-se:
2
2
− h= 2
E
m 2

2. ,

3. , i t − kx
53
e introduzindo-se a constante
k = 2mE
2 h
(5.2)
a equação anterior pode ser rescrita na seguinte forma:
d
dx
k
2
2
= 2 (5.3)
cujas soluções podem ser :
= Asen kx = A cos kx (5.4)
ou uma combinação linear dessas expressões que corresponde a uma solução mais geral. Assim :
= Asen kx + B cos kx (5.5)
é uma solução que contem quantidades imaginárias ou complexas.
Se lembrarmos que eikx = cos kx + sen kx e e−ikx = cos kx − sen kx a expressão (5.4) pode ser
apresentada na seguinte forma:
= A,eikx + B,e−ikx (5.6)
Na verdade esta solução é somente uma parte da solução, é a parte espacial. Se lembrarmos que toda onda
tem uma freqüência , podemos acrescentar um termo de variação temporal multiplicando a expressão
anterior por e−2it e obter uma nova função, agora porém com a seguinte forma:
= A,eikx e2it + B,e−ikx e2it
substituindo 2 = ela se torna:
=
+
+

4. A e
i t kx
B e
(5.7)
Para se interpretar este resultado, que é a solução do problema proposto, pode-se observar que a equação
(5.7) representa a soma de duas ondas progressivas. Aquela correspondente ao primeiro termo é uma onda
que está se movendo no sentido negativo do eixo x com uma certa amplitude A’ e aquela representada pelo
segundo termo refere-se a outra onda com amplitude B’ movendo-se no sentido positivo. Esta soma
representa uma onda estacionária cuja amplitude depende das amplitudes A’ e B’.
É importante agora determinar-se a energia da partícula livre. Lembrando que o número de onda k vale 2
/ e comparando com o valor de k obtido da equação (5.2) obtém-se a seguinte igualdade:
2 2
2
= mE
h
que implica em E
2
= h2 m
2
ou

5. 54
E
p
m
=
2
2
(5.8)
onde p é o momento linear de uma partícula.
Pode-se perceber que não existe nenhuma restrição aos valores de p e portanto aos da energia E. Isso é
conseqüência do fato de não ter sido imposta nenhuma condição de contorno já que o potencial era nulo em
todo o espaço.
Classicamente a energia de uma partícula livre é sua própria energia cinética E = mv
2
2
que pode ser escrita
da mesma forma que a expressão quântica (5.8). O gráfico de E em função do momento linear está
representado por uma linha contínua na figura 5.1.
Fig. 5.1 -Energia de uma partícula em função de seu momento linear para uma partícula livre (---) e para uma
partícula numa caixa ( ).
5.3 POÇO DE POTENCIAL INFINITO
O poço de potencial infinito é um problema bastante simples mas de grande significado que pode ser
resolvido utilizando-se a equação de Schrödinger .
Na prática esse tipo de potencial não existe mas ele pode ser utilizado para tratar partículas fortemente
ligadas, ou seja, partículas que precisariam receber uma grande energia para se desligar, pois nesse caso o
poço infinito é uma boa aproximação.
Esse potencial pode ser representado pela figura 5.2, ao lado onde :
para x 0 e x L V =
e para 0 x L V = 0
Pode-se tentar agora encontrar a função de onda que descreve o comportamento de uma partícula submetida
a esse potencial a partir da equação de Schrödinger, substituindo o valor de V.
Fig. 5.2 – Potencial de uma partícula presa numa caixa de largura L e altura infinita

6. ( ) − ( ) ( ) ( )
+ = h2
2
= com n= 1,2,3.... (5.9)
55

8. 2
d x
dx
m 2
V x x E x
Analisando o problema nas diferentes regiões:
para x 0 e x L a função deve ser nula porque a partícula não pode estar nessa região, então a solução é
1 = 0 ;
para 0 x L a equação é igual a de uma partícula livre d
dx
k
2
2
= 2 cujas soluções possíveis são:
2 (x) = Asen kx 2 (x) = Acos kx (5.4)
Chegado a esse ponto é necessário impor as condições de continuidade nas fronteiras do poço. Essas
condições impõe que a função de onda válida à esquerda do ponto zero apresente o mesmo valor que a
função de onda válida direta para x = 0; essa mesma condição deve valer no ponto x = L que é uma outra
fronteira, assim como para as derivadas das funções de onda. Essas condições implicam que na fronteira não
pode haver nem descontinuidade na função de onda nem mudança brusca na sua inclinação.
Desse modo a continuidade da função de onda implica em:
1(x) = 2 (x) tanto para x = 0 1(0) = 2 (0)
como para x = L 1(L) = 2 (L)
que por sua vez implica em : 0 = Asen(k.0) e 0 = Bcos(k.0)
dessas duas condições só a primeira é possível para valores de A não nulos, então consideraremos como
válida a solução
2 (x) = Asen kx
Impondo-se a essa função a condição de continuidade em L obtém-se:
1(L) = 2 (L) 0 = A sen (kL) kL = n
kn
n
L
Isso quer dizer que só alguns valores de número de onda, k, são aceitáveis, os que obedecem às condições de
contorno. Assim nossa função de onda solução do problema dentro do poço é:
(x)n = Asen knx (5.10)
Para determinar o valor de A é preciso impor a condição de normalização (4.27), qual seja, a integral da
densidade de probabilidade da função de onda sobre todo o eixo x deve ser igual a um. o significado da
normalização é que afirma-se que a probabilidade da partícula estar em algum

9. ponto do eixo é 1, ou seja, seguramente a partícula está em algum ponto do espaço.
L L
= = =
2 2
PdV dV A (knx)dx
L
=
L
= pode-se provar que sen2 ( )
= 2
n
56
0
1
0
0
sen
sen2 ( ) 1
0
2 knx dx
A
2
0
knx dx L
donde se obtém, como resultado da normalização: A
L
Portanto a solução para o poço infinito é:
( )
2
( ) x
L
sen
L
x n
= onde n = 1,2,3..... (5.11)
determinando-se a energia correspondente utilizando-se as equações (5.2) e (5.9) chega-se a:
E h n
mL
=
2 2
8 2
onde n = 1,2,3..... (5.12)
Esta expressão (idêntica à 3.51) significa que a energia de uma partícula num poço de potencial infinito é
quantizada e seu valor no estado fundamental (para n = 1) não é nula, ou seja, a energia mínima não é zero.
Isto está coerente com o princípio de incerteza que diz que se fosse possível determinar o momento, e
portanto a energia, com incerteza zero, E poderia ser nula, e a incerteza na posição deveria ser infinita.
Estes valores colocados num gráfico de E em função de p (momento linear) correspondem aos pontos na
figura 5.1. O fato dos pontos caírem exatamente sobre a curva traçada para uma partícula livre significa que
os valores de energia que uma partícula numa caixa de paredes infinitas pode ter são os mesmos que os de
uma partícula livre, com a diferença que nem todos são permitidos.
Também podem ser obtidos os gráficos da função de onda (equação 5.11) e da densidade de probabilidade
(equação 4.26) para diversos valores de n, figura 5.3.
Não é possível obter significado físico do gráfico de pois pode ser uma função imaginária, porém a curva
que representa a densidade de probabilidade P = indica para cada valor de x a densidade de
probabilidade da partícula estar naquele ponto. O valor de n está associado ao estado, assim n = 1 indica o
estado 1 cuja energia é E1 e cuja função de onda é 1 e assim sucessivamente. Como pode ser observado,
para uma partícula dentro de um poço de potencial infinito a probabilidade dela estar fora da caixa é zero.

10. Fig. 5.3 - Função de onda e densidade de probabilidade para uma partícula num poço de potencial infinito
para os valores de n =1 curva (a), n =2 (curva b) e n =3 curva (c)
57
5.4 POÇO DE POTENCIAL FINITO
Tornando mais realístico o modelo de uma partícula num poço de potencial o suporemos de valor finito, ou
seja, como se as paredes da caixa não fossem perfeitamente rígidas.
Fig. 5.4. - Potencial para um poço finito de largura L
A formulação é basicamente a mesma que no caso anterior, só que agora o potencial não é infinito, mas sim
V0, então a função de onda fora do poço não é nula. Impondo esse valor à equação de Schrödinger chegamos
à diferentes tipos de equações e, portanto, diferentes soluções em cada região.

11. = A ex + B e−x (5.13)
= A ex + B e−x (5.15)
sen kL + B
cos kL = B
e-
kA kL kB sen kL B e- aL
58
Para x 0 e x L V =V0
2
0
( ) ( mE
x
) E (x)
V m
d x
dx
−
− =
2
2
2
2
2
h h
ou
( ) ( ) d x
dx
2 0
x
2
2
− = onde
( )
=
2 −
0 m V E
2
h
e para 0 x L V = 0
( ) ( ) d x
dx
2 0
k x
2
2
+ = onde k = 2mE
2 h
Escrevendo as soluções em cada região obtém-se:
para x 0 − − −
para 0 x L 0 0 0 = A sen kx + B coskx (5.14)
para x L + + +
Para determinar os valores das diferentes constantes A- , B- , A+ , B+ , A0 e B0 , é preciso impor as condições
de contorno à essas soluções, que, no caso, são a exigência de continuidade da função de onda e de sua
derivada nos pontos x = 0 e x =L , ou seja, a solução pela esquerda deve coincidir com a solução pela
direita nesses pontos, o mesmo devendo ser imposto à derivada da função de onda. Isso pode ser escrito da
seguintes forma:
− (x = 0) = 0 (x = 0) e ( ) ( ) 0 x = L = + x = L
0
( ) ( )
d
dx
x
d
dx
x
−
=
=
0 =
0
e
( ) ( )
d
dx
x L
d
dx
x L
0
=
= +
=
É preciso impor também que, para x tendendo a infinito, a função de onda tende a zero, o que significa que a
probabilidade de se encontrar a partícula num ponto distante da caixa diminui a medida que esse ponto se
afasta da caixa. Isto pode ser escrito como:
− (−) = 0 o que implica em que B
−
= 0
+ (+) = 0 o que implica em que A
+
= 0
Impondo as condições de contorno às soluções obtém-se:
=
A B
−
0 A aL
0 0
+
A = kA
−
0
+
= -
0
cos -
0

12. sen cos que implica em tg kL
59
substituindo B A k A
0
=
−
=
0 e dividindo toda a expressão por - obtém-se:
A sen kL + k
A cos kL =
B e -
aL
0 0
+
k 2 A sen kL - k
A cos kL =
B e -
aL
2 0 0
+
Igualando os primeiros termos dessas equações chega-se a:
2
2
A k kL kL
0
1 - + 2 k = 0

13. sen cos
Como A0 não pode ser nula senão A0 e B0 também seriam nulos, a expressão entre colchetes deve ser igual a
zero:
2 2 - = - 2 k k kL kL

14. = 2k
k
2 − 2
Fazendo uma mudança de variáveis : 0
0 2
2
=
mV
h
e = E
V
0
pode-se escrever: = − 0 1 k = 0
donde se obtém:
( ) (
)
2 1
= 2
−
( )
( )
2 1
2 1
1
0
0
2
−
=
0 −
− +
tg L
esta equação tem solução numérica porém pode ser resolvida através de solução gráfica como será mostrado
a seguir.
Chamando-se os dois termos da equação acima de f() chega-se a:
tg ( L ) = f ()
0 (5.16)
( )
−
−
( ) 2
1
2 1
= f (5.17)
o gráfico de f() em função de (figura 5.5) fornece duas curvas, uma para cada função. A solução deste
problema é dada pelos valores de e de f() correspondentes aos pontos comuns às duas curvas, ou seja,
aos pontos de intercessão que são os valores que satisfazem simultaneamente as duas funções.
A solução pode ser analisada para diversos valores de V0.
Se V0 for pequeno o poço é raso e nesse caso pode-se supor que V
2 2
2 2
h o que implica
0 mL

15. L = e nesse caso se variar de 0 a 1 , 0L variará de zero a
2 2
2 2
60
mV L
h
que 2
2
ou seja 0L .
A título de exemplo suporemos
0 4
/4 e a tg( L ) 0 variará de zero a tg (/4) que é igual a 1. Na figura 5.5 o gráfico de f() em função de
de acordo com a equação (5.16) é representado pela linha tracejada e de acordo com a equação (5.17) pela
linha contínua. Essa última apresenta uma descontinuidade no ponto = 0,5. Nesse caso há somente uma
solução, aquela correspondente ao ponto de cruzamento duas linhas, que acontece para = 0,87, ou seja E =
0,87V0.
Fig. 5.5 - Gráfico de f() em função de de acordo com as equações (5.16) e (5.17)
Se for considerado um poço de potencial mais profundo, sendo a tangente uma função cíclica de seu
argumento haverá mais pontos de intercessão entre as duas curvas o que dará origem a um maior número de
soluções, ou seja , a um número maior de energias permitidas à partícula que está dentro da caixa de paredes
não rígidas.
Esquematicamente a solução do problema pode ser apresentada como no diagrama da figura 5.6, quanto mais
profundo o poço mais níveis permitidos tem a partícula que está dentro dele. Os valores de V0 usados em
cada caso são:
a) poço raso
=
L = V h
0 4
0 mL

16. = h
61
b) poço com profundidade maior
0
13
4
L = V
169 2 2
2 2
= h
0 mL
c) poço ainda mais profundo
0
33
4
L = V
1089 2 2
2 2
0 mL
Fig. 5.6 - Diagrama dos níveis de energias permitidos à uma partícula dentro de uma caixa de paredes não
rígidas
Comparando estes resultados com aqueles obtidos para o poço infinito (figura 5.3) encontram-se algumas
diferenças fundamentais nas funções de onda e nas densidades de probabilidade, no poço infinito as duas se
anulam fora do poço (figura 5.3) enquanto no poço finito (figura 5.7) tendem a zero suavemente fora do
poço, o que significa que a probabilidade de encontrar a partícula fora do poço pode não ser nula, como
descrito na mecânica clássica.
Fig. 5.7 - Função de onda e densidade de probabilidade para uma partícula num poço de potencial finito para
os valores de n =1 curva (a), n =2 (curva b) e n =3 curva (c)

17. 62
5.5 DIVERSOS TIPOS DE POTENCIAL
No caso estudado na seção anterior a energia da partícula era inferior a V0, ou seja, a partícula estava presa
dentro do poço de potencial. Agora será considerado o caso de E V0,, ou seja, partícula livre.
Um elétron livre movendo-se próximo a uma região onde há um poço de potencial pode ser encarado como
uma onda deslocando-se e encontrando esse poço em seu caminho. O formato desse potencial é muito
variável, podendo até se constituir numa barreira.
5.5.1 - Poço de potencial
Classicamente se a energia da partícula é inferior a profundidade do poço, E V0, ela está presa dentro dele
e se for superior, E V0,, estará livre, mas em ambos os casos ela poderá ter qualquer valor de energia.
Quanticamente as coisas se passam de outro modo, já foi visto que quando E V0 os valores de energia da
partícula são quantizados ou seja, nem todos os valores são permitidos. Quando E V0 o poço de potencial
influi no comportamento da partícula ainda que ela seja livre.
A óptica ensina que, quando o comprimento de onda muda repentinamente (numa pequena distância
comparada com o comprimento de onda), parte da onda é refletida e parte é transmitida. Esse
fenômeno acontece com a função de onda quando ela encontra a fronteira do poço de potencial
porque aí sua energia é alterada. Nesse caso as funções de onda serão influenciadas pela presença do poço
fazendo com que haja reflexão de parte dela em cada fronteira do poço como mostra a figura 5.8.
Fig. 5.8 - Onda aproximando-se de um poço de potencial : (a) onda (b) função de onda

18. h
p
= =
63
5.5.2 - Potencial degrau
Um elétron ao se deslocar ao longo do eixo x encontra à sua frente um potencial com o formato
indicado na figura 5.9, esse problema é estudado tanto pela mecânica clássica quanto pela mecânica
quântica.
Fig. 5.9 - Elétron aproximando-se Fig. 5.10 - Função de onda com energia de um
potencial degrau E V0 penetrando na barreira
Classicamente uma partícula com energia E ao se aproximar de uma barreira de potencial V0 a
ultrapassará se E V0 ficando com uma energia (E - V0) e retornará se tiver uma energia E V0.
Para visualizar isso imaginemos a barreira com o formato de uma colina, se a energia da partícula
for menor que a da barreira, a partícula diminui sua velocidade até parar sem chegar ao topo
retornando em seguida.
Quanticamente pode-se fazer a imagem de uma onda com uma energia E aproximando-se da
barreira. Se E V0 a função de onda tende a zero além da barreira havendo uma probabilidade não
nula da partícula se encontrar aí, como no caso do poço finito (figura 5.10). Se E V0 o
comportamento clássico é diferente do quântico, em x = 0 o comprimento de onda muda
abruptamente de 1
1
1
2
= h =
p
h
mE
para
h
1
m E V
( )
2
2
−
2 0
porque a energia de onda muda de
E para E - V0.
A probabilidade da reflexão e a amplitude das ondas refletidas e transmitidas podem ser obtidas
através da equação de Schrödinger. Isto, porém, não será feito aqui por fugir do escopo deste livro,
que simplesmente deseja mostrar que tipo de resultados podem ser obtidos a partir da equação de
Schrödinger. A figura 5.11 mostra como se comporta a função de onda de uma partícula com energia
superior à barreira ao tentar ultrapassá-la.
Fig. 5.11 - Função de onda com energia E V0 chegando a uma barreira

19. 64
5.5.3 Barreiras de potencial
Este problema é semelhante ao degrau de potencial com a diferença que a largura do degrau é finita.
Se E V0 , classicamente a partícula não tem condições de atravessar a barreira mas quanticamente a
probabilidade que isso aconteça não é nula, ou seja a partícula pode atravessar uma barreira ainda que sua
energia seja inferior. Este fenômeno é chamado tunelamento e é aproveitado na construção dos diodos de
tunelamento. Isto ocorre porque se a barreira não for infinita existe uma probabilidade que a partícula a
penetre.
Fig. 5.12 - Potencial degrau (a); função de onda de uma partícula que o atravessa (b)
5.6 OSCILADOR HARMÔNICO
Ao se considerar, classicamente, uma partícula presa a uma mola dizemos que a força que atua sobre ela é do
tipo F = kx e o potencial a que está submetida é V = Fdx = kx
2
2
.
O gráfico da distribuição da probabilidade de encontrar essa partícula ao longo de seu percurso é
inversamente proporcional a sua velocidade dando uma curva do tipo dada abaixo.
Fig. 5.13 – Probabilidade de encontrar a
partícula, presa a uma mola, na posição x.
Ainda classicamente pode-se dizer que o espectro das energias possíveis é contínuo variando de
zero a kL2
2
.
Quanticamente esses dados podem ser obtidos através da equação de Schröedinger:
( ) ( ) ( ) kx x E x
2 h
d x
m
dx
2
+ =
−
2
2
2
2

20. n n Hn y e
− mh
65
que rescrita dá:
d ( x
) m
E kx ( x
) dx
2
2
2
2
2
2
0

21. + −
=
h
fazendo-se 2 2
= m E
2
h
e y2 mk x
= 2
2
h
obtém-se:
d ( x
) y ( x
) dx
2
2
2 2 0
+ −

22. =
As soluções desse tipo de equação diferencial baseiam-se nos polinômios de Hermite e são soluções que
podem ser encontradas tabeladas. São do tipo:
m
h
n ( )
y
=

23. −
2
1
4 2
2
! 2 (5.18)
A título de exemplo daremos abaixo os seis primeiros polinômios de Hermite e algumas das funções de
onda:
TABELA 5.1. - OS SEIS PRIMEIROS POLINÔMIOS DE HERMITE QUE SÃO PARTE DAS FUNÇÕES
DE ONDA DO OSCILADOR HARMÔNICO
2 En n
N Hn(y)
0 1 1 h/2
0 ( 2
)
1
4
2
= e
2
y
1 2y 3 3h/2 ( 2
)
1 1
4
4
2
−
= 2
mh
ye
y
2 4y2 - 2 5 5h/2 ( 1
2
) 4
( 2 )
2 8 4 2
2
−
= − 2
mh
y e
y
3 8y3 - 12y 7 7h/2 ( 1
2
) 4
( 3 )
3 48 8 12
2
−
= − 2
mh
y y e
y
4 16y4 -48y2 +12 9 9h/2
5 32y5 - 16y3 +120y 11 11h/2
Abaixo nas figuras 5.14 e 5.15 estão esboçadas as funções de onda e a probabilidade clássica e quântica de
encontrar uma partícula na posição x para diversos valores de n.
Fig. 5.14 - Funções de onda para n = 0 (a); n =1 (b) e n = 10 (c )

24. Fig. 5.15. - Probabilidade quântica ( ) e probabilidade clássica ( - ) para os estados n =0 e n =1 e n =
10 de um oscilador harmônico.
Pode-se observar que, à medida que o número quântico aumenta, a probabilidade quântica se aproxima da
probabilidade clássica.
1
2
66
Os níveis de energia permitidos são dados por
En n h = +

25. onde n = 0,1,2,3.... (5.19)
O menor valor de energia de uma partícula presa nesse tipo de poço de potencial pode ter é E
o
= h
2
, o que
significa que a partícula não pode ter energia nula, contrariamente ao que tinha sido encontrado
classicamente.
Outra diferença é que os valores possíveis de energia não são contínuos mas sim discretos e eqüidistantes de
h/2 . Lembrando que a freqüência de oscilação de um sistema massa-mola depende diretamente do valor da
constante da mola, k, e indiretamente da massa, m pode-se notar que os valores dos níveis de energia
permitidos e o seu número depende da relação k/m, da profundidade e da largura do poço. Isto pode ser
notado se for lembrado que a profundidade do poço é dada pela energia total do sistema que é sua energia
potencial máxima, kL2
2
, que por sua vez depende do valor a largura do
poço.
O diagrama da figura 5.16, abaixo, apresenta os níveis de energia permitidos . Note-se a diferença entre esse
diagrama e o correspondente para o poço de potencial finito.
Fig. 5.16 – Diagrama de energias possíveis para um oscilador
harmônico.
E E hv n n − = −1

26. , , x, y, z
* + sen , ,
, , r
67
5.7 ÁTOMO DE HIDROGÊNIO
A primeira descrição do modo de funcionamento de um átomo de hidrogênio foi feita por Bohr de forma
empírica e intuitiva. Aqui, agora, será feita uma outra descrição, a partir da equação de Schrödinger que já é
bem conhecida de todos.
5.7.1 Solução da Equação de Schrödinger
O primeiro passo para encontrar a função de onda que descreve o comportamento do elétron é determinar a
que potencial ele está submetido. O elétron está no campo elétrico criado pelo próton e portanto o potencial
ao qual ele está submetido é:
V e
r
Ke
r
= − = −
4
0
(
(5.20)
Esse potencial tem simetria esférica sendo, portanto, conveniente escrever a equação de Schrödinger em
coordenadas esféricas.
Até aqui utilizou-se a equação simplificada para problemas unidimensionais mas o átomo de hidrogênio será
tratado tridimensionalmente o que obriga que ela seja escrita da seguinte forma:
− ) + − = h2
2
2 0
m
(V E) 5.21)
onde )2 é o laplaciano da função . O laplaciano em coordenadas cartesianas e esféricas polares é
respectivamente:
) ( ) = + + ( )
2 2
2
2
2
2
2
x y z
x y z
(5.22)
( ) ( ) ) =

27. + +

28. 2 1
2
2 1
2 2
2
2
1
2
r
r r
r
r r r
sen sen
*
+ *
*
*
*
* + (5.23)
No caso unidimensional a equação (5.21) transforma-se na equação (4.25) já conhecida.
Como o átomo de hidrogênio tem simetria esférica pode-se pensar que cada variável é independente e
portanto a função de onda genérica seria formada pelo produto de funções, cada uma delas dependente só de
uma das variáveis, como a seguir:
(r,*,.) = ,(.)-(*)R(r) (5.24)
Esse tipo de função permite que se encontre a solução da equação de Schrödinger pelo método das variáveis
separáveis, com relativa facilidade, como pode ser visto no apêndice A. Após o citado desenvolvimento
chega-se a:

29. * = * * (5.26)
Zr
na
o Zr
r * . = R r * .
68
im .
, ( )
m
e
.
= onde m = 0,1,2,3.... (5.25)
- ( ) ( sen ) ( cos
)
l, m
l
m F
m
onde l deve obedecer à seguinte condição: l = m, m + 1, m + 2, m + 3.....e onde F
lm
são as funções
associadas de Legendre apresentadas no apêndice B.
R ( )
n l
r e
Zr
na
o Zr
na
o
L
n
Zr
na
o
,
=
−

32. 2 2
l
(5.27)
onde L
nl
são os polinomiais de Laguerre, também apresentados no apêndice B, e ao é o primeiro raio de
Bohr igual a
4
0
a
0 e
2
2
=
(
μ
h
Substituindo-se todas essas expressões na equação (5.24) obtém-se a solução geral para o átomo de
hidrogênio:

36. (r ) e ( ) ( )
na
o
L
n
Zr
na
o
m F
m
e
im
,*,+ sen * cos*
.
=
−
2 2
l l
(5.28)
Com as restrições que n, l e m são inteiros sendo n e l sempre positivos, com l variando de zero a (n -1)
e m variando de - l a l , o que pode ser representado esquematicamente por:
número quântico principal n = 1,2,3....
número quântico azimutal l = 0,1,2,......(n-1)
número quântico magnético m = - l , - l +1, - l +2, .....,0,..... l +2, l +1, l
A título de curiosidade no apêndice B estão as expressões que permitem determinar algumas das funções
polinomiais de Legendre e de Laguerre.
5.7.2 Energia do elétron
O elétron vai ter um valor de energia diferente em cada órbita. Para se determinar esse valor deve-se voltar à
equação de Schrödinger substituindo a função de onda solução e determinando o valor de E. A título de
exemplo consideremos o elétron que tem o seguinte conjunto de números quânticos: n = 2; l = 1; m = 1, ou
seja cuja função de onda é
( , ,
) ( )- ( ), ( )
2,1,1 2 , 1 11 ,
1
ou

37. Zr
a
o Zr
2 1
= * .
* + i
( ) ( )
2 11
+ = h2
2
69
8
3
2
, ,
r, , e sen
a
o
Z
a
o
e
−

40. determinando-se todas as derivadas de e substituindo-se na equação 5.23 e depois na 5.21 chega-se a

43. − − +
−
2 1
2
1
0
1
8
0
2
2
μ r ra a r 2
V E
que nos permite deduzir que E V
a
o
r a
o

45. = + −
h2 1 1
μ 8
e lembrando-se do valor de V da equação 5.20 chega-se ao valor da energia do elétron com número atômico
principal n =2:
E
e
o
2
4
8 4
2
2
= −

46. μ
( h
uma generalização dessa expressão para qualquer valor de n permite chegar a:
E
n
Z e
o
n
= −