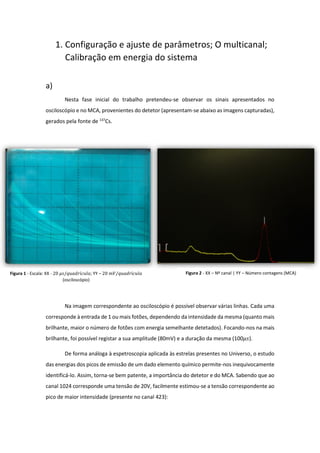
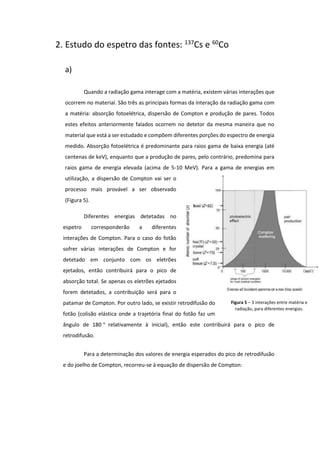
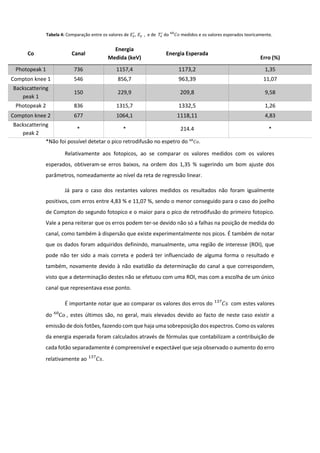
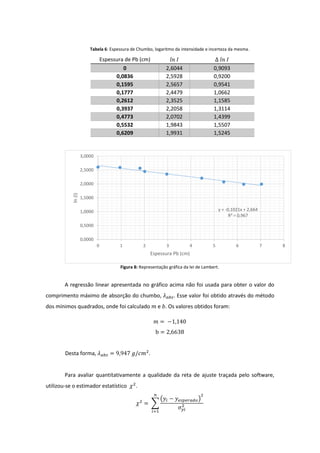
O documento apresenta um estudo sobre a espectroscopia gama com foco na configuração de um sistema de detecção e calibração utilizando fontes radioativas. Descreve a interação da radiação gama com a matéria, a determinação de picos de absorção e a atenuação de radiação em diferentes espessuras de chumbo. Os resultados incluem comparações entre dados medidos e esperados, com considerações sobre erros experimentais e métodos de calibração.

1. INSTITUTO SUPERIOR TÉCNICO
Física da Radiação
Espetroscopia γ
Mestrado Integrado em Engenharia Biomédica
João Amorim Nº 78235
Luís Rita Nº 78680
Rodrigo Mateus Nº 78963

2. 1. Configuração e ajuste de parâmetros; O multicanal;
Calibração em energia do sistema
a)
Nesta fase inicial do trabalho pretendeu-se observar os sinais apresentados no
osciloscópio e no MCA, provenientes do detetor (apresentam-se abaixo as imagens capturadas),
gerados pela fonte de 137
Cs.
Na imagem correspondente ao osciloscópio é possível observar várias linhas. Cada uma
corresponde à entrada de 1 ou mais fotões, dependendo da intensidade da mesma (quanto mais
brilhante, maior o número de fotões com energia semelhante detetados). Focando-nos na mais
brilhante, foi possível registar a sua amplitude (80mV) e a duração da mesma (100𝜇𝑠).
De forma análoga à espetroscopia aplicada às estrelas presentes no Universo, o estudo
das energias dos picos de emissão de um dado elemento químico permite-nos inequivocamente
identificá-lo. Assim, torna-se bem patente, a importância do detetor e do MCA. Sabendo que ao
canal 1024 corresponde uma tensão de 20V, facilmente estimou-se a tensão correspondente ao
pico de maior intensidade (presente no canal 423):
Figura 1 - Escala: XX - 20 𝜇𝑠/𝑞𝑢𝑎𝑑𝑟í𝑐𝑢𝑙𝑎; YY – 20 𝑚𝑉/𝑞𝑢𝑎𝑑𝑟í𝑐𝑢𝑙𝑎
(osciloscópio)
Figura 2 - XX – Nº canal | YY – Número contagens (MCA)

3. 20
1024
≈ 0,020𝑉
0,020 × 423 = 8,46𝑉
Sabendo que se amplificou o sinal proveniente do detetor × 128, seria de esperar obter
uma tensão a rondar os 10,24V (pois a amplitude do sinal registado no osciloscópio é,
aproximadamente, 0,08V). Apesar de tudo, é um erro aceitável, dada a imprecisão da leitura da
amplitude efetuada no osciloscópio.
Assim, cada linha curva observada no osciloscópio encontra-se quantificada no MCA
pelo número de contagens. Perdendo-se apenas a dimensão temporal da amostra, uma vez que
a aquisição de imagens com o auxílio do PC é feita apenas para certos intervalos de tempo.

4. b)
A percentagem de erro obtido na tabela acima foi fornecida pelo próprio software. Uma
vez que se registou a área e não o integral de cada pico, existirá um erro adicional ao estatístico,
que decorre do facto de terem sido feitas algumas aproximações de forma a não incluir
contagens de radiação não emitidas pelo isótopo. Isto é sustentado, pelo facto do número de
contagens relativas a este parâmetro ser sempre superior ao valor da área.
De forma a obter-se uma relação entre o número de cada canal e a respetiva energia do
fotão associada, obteve-se uma reta de calibração, resultante do conhecimento da energia e
canal dos picos de radiação X e gama do césio. Tal como
se pode observar, esta última corresponde já a uma
transição do átomo de Bário. Por outro lado, a transição
que origina a radiação X, não se encontra descrita na
figura _.
Pico
Energia
(keV)
Centróide
(canais)
Largura total a meio
máximo FWHM
(canais)
FWHM (keV) R
Área (#
contagens por
baixo do pico)
X-ray 32 25 4,606 7,291 0,228 151904 ± 0,31%
𝜸-ray 662 423 28,856 38,104 0,058 327133 ± 0,20%
𝐸𝑛𝑒𝑟𝑔𝑖𝑎 = 1.583 × 𝐶𝑎𝑛𝑎𝑙 − 7.573
Tabela 1 – Vário valores associados aos picos registados do átomo de Césio.
Figura 3 – Reta de calibração.
Figura 4 – Algumas transições presentes entre
diferentes níveis no átomo de 137Cs.
Energia
Canal

5. Após aplicação da fórmula: 𝑅 =
∆𝐸
𝐸
=
𝐹𝑊𝐻𝑀
𝐸
, determinou-se a resolução do primeiro e
do segundo pico. De forma a poder-se proceder a este cálculo, teve-se primeiro de converter o
valor da largura total do pico a média altura, para as mesmas unidades em que a energia se
encontra expressa (keV). Para tal, recorreu-se à equação da reta obtida anteriormente. Tanto a
resolução, como os valores do FWHM encontram-se expostos na tabela I.
Por fim, estimou-se o erro na posição de ambos os centróides. Para tal, utilizou-se a
fórmula (3), onde se teve em conta o FWHM, bem como o número total de contagens por baixo
de cada pico (área).
𝜎 𝑝𝑐
2
=
𝜎2
𝑁
(1)
𝜎 =
𝐹𝑊𝐻𝑀
2,35
(2)
𝜎 𝑝𝑐 =
𝐹𝑊𝐻𝑀
2,35√𝑁
(3)
A tabela abaixo apresenta estes erros.
Pico Energia (keV) Centróide
(canais)
FWHM
(keV)
Área (# contagens por
baixo do pico)
𝝈 𝒄𝒆𝒏𝒕𝒓ó𝒊𝒅𝒆
(keV/contagens)
X-ray 32 25 7,291 151904 ± 0,31% 0,008
𝜸-ray 662 423 38,104 327133 ± 0,20% 0,028
Tabela 2 – Valores utilizados para o cálculo dos erros e respetivos erros.

6. 2. Estudo do espetro das fontes: 137
Cs e 60
Co
a)
Quando a radiação gama interage com a matéria, existem várias interações que
ocorrem no material. São três as principais formas da interação da radiação gama com
a matéria: absorção fotoelétrica, dispersão de Compton e produção de pares. Todos
estes efeitos anteriormente falados ocorrem no detetor da mesma maneira que no
material que está a ser estudado e compõem diferentes porções do espectro de energia
medido. Absorção fotoelétrica é predominante para raios gama de baixa energia (até
centenas de keV), enquanto que a produção de pares, pelo contrário, predomina para
raios gama de energia elevada (acima de 5-10 MeV). Para a gama de energias em
utilização, a dispersão de Compton vai ser o
processo mais provável a ser observado
(Figura 5).
Diferentes energias detetadas no
espetro corresponderão a diferentes
interações de Compton. Para o caso do fotão
sofrer várias interações de Compton e for
detetado em conjunto com os eletrões
ejetados, então contribuirá para o pico de
absorção total. Se apenas os eletrões ejetados
forem detetados, a contribuição será para o
patamar de Compton. Por outro lado, se existir retrodifusão do
fotão (colisão elástica onde a trajetória final do fotão faz um
ângulo de 180 ° relativamente à inicial), então este contribuirá para o pico de
retrodifusão.
Para a determinação dos valores de energia esperados do pico de retrodifusão
e do joelho de Compton, recorreu-se à equação de dispersão de Compton:
Figura 5 – 3 interações entre matéria e
radiação, para diferentes energias.

7. 𝐸 𝛾
′
=
𝐸 𝛾
1 +
𝐸 𝛾
𝑚 𝑒 𝑐2 (1 − cos 𝜃)
Sendo que 𝜃 representa o ângulo da trajetória do fotão refratado em relação à
sua trajetória inicial, 𝑚 𝑒 a massa do eletrão e 𝑐 a velocidade da luz.
Quando 𝜃=180º há inversão da trajetória, sendo esta chamada de retrodifusão podendo
calcular-se através da substituição do valor na equação anterior:
𝐸 𝛾
′
=
𝐸 𝛾
1 + 2
𝐸 𝛾
𝑚 𝑒 𝑐2
Já para o cálculo do valor esperado do “joelho” de Compton, sabe-se que 𝑇𝑒′ = 𝐸 𝛾 − 𝐸 𝛾′,
logo:
𝑇𝑒
′
= 𝐸 𝛾 −
𝐸 𝛾
1 + 2
𝐸 𝛾
𝑚 𝑒 𝑐2
Os valores experimentais da energia foram determinados a partir da reta de
calibração apresentada no primeiro grupo, e a energia esperada foi determinada
considerando que 𝐸 𝛾=662 keV.
Ao observar e comparar os valores obtidos com os valores esperados de energia
para o joelho de Compton e o pico de retrodifusão, verifica-se que existiu um erro menor
para a energia do joelho de Compton que para o pico de retrodifusão. Isto pode dever-
se a um erro na determinação do canal ou outros erros associados ao equipamento
utilizado.
Cs Canal
Energia Medida
(keV)
Energia Esperada Erro (%)
Joelho de Compton 293 456,2 477,39 4,44
Pico de retrodifusão 137 209,3 184,61 13,38
Tabela 3: Comparação entre os valores de 𝐸 𝛾
′
e de 𝑇𝑒
′
do 137Cs medidos e os valores esperados teoricamente.

8. b)
Nesta parte da atividade laboratorial, adquiriu-se durante 600s um espetro da
fonte de Co60
usando a calibração no início da atividade. Sabendo os canais
correspondentes, foram determinados as energias dos fotopicos do cobalto, as energias
dos picos de retrodifusão e as energias dos joelhos de Compton e compararam-se com
os valores teóricos.
Como é possível observar-se, o patamar de Compton do primeiro fotopico apresenta-se
entre (1) e (2), ao passo que o patamar de Compton do segundo fotopico encontra-se entre (1)
e (3).
Na tabela seguinte estão os valores para a energia medida e a esperada, para os cinco
pontos relevantes. Os valores de energia esperados (𝐸 𝛾1=1173.2 keV e 𝐸 𝛾2=1332.5 keV) foram
obtidos a partir da figura 7.
(1)
(3)
(4)
(5)(2)
Figura 6 - Espetro do Co60
. (1) Pico de retrodifusão 1, embora teoricamente sejam dois; (2) Joelho de Compton 1; (3) Joelho de Compton 2; (4)
Fotopico 1; (5) Fotopico 2
Figura 7 - Algumas transições presentes entre
diferentes níveis no Cobalto

9. *Não foi possível detetar o pico retrodifusão no espetro do 𝐶𝑜60
.
Relativamente aos fotopicos, ao se comparar os valores medidos com os valores
esperados, obtiveram-se erros baixos, na ordem dos 1,35 % sugerindo um bom ajuste dos
parâmetros, nomeadamente ao nível da reta de regressão linear.
Já para o caso dos restantes valores medidos os resultados não foram igualmente
positivos, com erros entre 4,83 % e 11,07 %, sendo o menor conseguido para o caso do joelho
de Compton do segundo fotopico e o maior para o pico de retrodifusão do primeiro fotopico.
Vale a pena reiterar que os erros podem ter-se devido não só a falhas na posição de medida do
canal, como também à dispersão que existe experimentalmente nos picos. É também de notar
que os dados foram adquiridos definindo, manualmente, uma região de interesse (ROI), que
pode não ter sido a mais correta e poderá ter influenciado de alguma forma o resultado e
também, novamente devido à não exatidão da determinação do canal a que correspondem,
visto que a determinação destes não se efetuou com uma ROI, mas com a escolha de um único
canal que representava esse ponto.
É importante notar que ao comparar os valores dos erros do 𝐶𝑠137
com estes valores
do Co60
, estes últimos são, no geral, mais elevados devido ao facto de neste caso existir a
emissão de dois fotões, fazendo com que haja uma sobreposição dos espectros. Como os valores
da energia esperada foram calculados através de fórmulas que contabilizam a contribuição de
cada fotão separadamente é compreensível e expectável que seja observado o aumento do erro
relativamente ao 𝐶𝑠137
.
Co Canal
Energia
Medida (keV)
Energia Esperada
Erro (%)
Photopeak 1 736 1157,4 1173,2 1,35
Compton knee 1 546 856,7 963,39 11,07
Backscattering
peak 1
150 229,9 209,8 9,58
Photopeak 2 836 1315,7 1332,5 1,26
Compton knee 2 677 1064,1 1118,11 4,83
Backscattering
peak 2
* * 214.4 *
Tabela 4: Comparação entre os valores de 𝐸 𝛾
′ , 𝐸 𝛾 , e de 𝑇𝑒
′ do 𝐶𝑜60
medidos e os valores esperados teoricamente.

10. 3. Estudo da atenuação de gamas na matéria
a)
Nesta parte do laboratório estudou-se a atenuação de radiação gama em folhas
de chumbo com diferentes espessuras usando a fonte de Césio.
Uma vez que as medidas do número de desintegrações de uma fonte radioativa
são experiências de contagens, a variável aleatória, N, assume uma distribuição de
Poisson. Assim, a incerteza destas medições é calculada por:
∆ 𝑁
𝑁
=
√𝑁
𝑁
=
1
√𝑁
< 𝜀
Como queríamos um erro 𝜀 inferior a 3%, foi necessário obter mais 1111
contagens por medição.
Foi escolhida uma Region of Interest (ROI) adequada e foram obtidas contagens
para várias espessuras de chumbo representadas na tabela seguinte.
Tabela 5: Espessura, tempo de medição, contagens e taxa de contagens, para várias espessuras de chumbo.
Folha de
Pb
Espessura
(mg/cm2
)
Espessura
(cm)
Intervalo de
Tempo (s)
Contagens
𝑁 ± ∆𝑁
Taxa de Contagens
𝑅 ± ∆𝑅
0 0 83,34 1127 ± 33,6 13,52 ± 0,40
A 947,7 0,0836 84,16 1125 ± 33,5 13,36 ± 0,40
B 1809,1 0,1595 87,7 1141 ± 33,8 13,01 ± 0,39
C 2014,7 0,1777 97,54 1128 ± 33,6 11,56 ± 0,34
A+B 2756,8 0,2431 106,64 1121 ± 33,5 10,51 ± 0,31
D 4465 0,3937 125,04 1135 ± 33,7 9,08 ± 0,27
D+B 6274,1 0,5532 161,68 1176 ± 34,3 7,27 ± 0,21
E 7042 0,6209 154,8 1136 ± 33,7 7,34 ± 0,22
b)
Através da Lei de Planck, é possível conhecer a intensidade (I) de um feixe de
fotões incidentes numa superfície perpendicular à direção de propagação. Esta
intensidade pode ser definida pela multiplicação do número de fotões incidentes (N),
por unidade de tempo e área, pela energia de cada fotão.
𝐼 = 𝑁ℎ𝜐

11. Ao atravessar um material, um feixe de fotões reduz o seu fluxo N uma vez que
os fotões podem ser removidos ou deflectidos da direção de propagação inicial. Sendo
𝑑𝑁 o número de fotões removidos por unidade de tempo e área é possível obter a
seguinte relação, tendo em conta que 𝑑𝑁 é proporcional à espessura do material
atravessado e ao fluxo de fotões 𝑁:
𝑑𝑁 = − 𝜇𝑁𝑑𝑥
Onde 𝜇 é uma constante característica do material, o coeficiente de absorção
que é dado pelo quociente da densidade do material 𝜌 pelo comprimento de onda de
absorção máxima 𝜆 𝑎𝑏𝑠.
𝜇 =
𝜌
𝜆 𝑎𝑏𝑠
Assim, integrando:
∫
𝑑𝑁
𝑁
= −𝜇 ∫ 𝑑𝑥
𝑋
0
⟺ 𝑁(𝑥) = 𝑁0 𝑒−𝜇𝑥
⟺ 𝐼(𝑥) = 𝐼0 𝑒−𝜇𝑥
𝑁
𝑁𝑜
A última equação traduz a Lei de Beer-Lambert e pode ser rescrita da seguinte
forma:
ln 𝐼 = −
𝜌
𝜆 𝑎𝑏𝑠
𝑥 + ln(𝐼0)
Onde:
𝑚 =
𝜌
𝜆 𝑎𝑏𝑠
b = ln(𝐼0)
De forma a obter os parâmetros 𝑚 e 𝑏 foi feito um ajuste linear pelo método
dos mínimos quadrados usados os dados apresentados na alínea anterior e
convertendo-os usando a relação:
ln 𝐼 = ln 𝑁ℎ𝜐
Os dados obtidos apresentam-se na tabela seguinte:

12. Tabela 6: Espessura de Chumbo, logaritmo da intensidade e incerteza da mesma.
Figura 8: Representação gráfica da lei de Lambert.
A regressão linear apresentada no gráfico acima não foi usada para obter o valor do
comprimento máximo de absorção do chumbo, 𝜆 𝑎𝑏𝑠. Esse valor foi obtido através do método
dos mínimos quadrados, onde foi calculado 𝑚 e 𝑏. Os valores obtidos foram:
𝑚 = −1,140
b = 2,6638
Desta forma, 𝜆 𝑎𝑏𝑠 = 9,947 𝑔/𝑐𝑚2
.
Para avaliar quantitativamente a qualidade da reta de ajuste traçada pelo software,
utilizou-se o estimador estatístico 𝜒2
.
𝜒2
= ∑
(𝑦𝑖 − 𝑦 𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑜)
2
𝜎 𝑦𝑖
2
𝑛
𝑖=1
Espessura de Pb (cm) 𝑙𝑛 𝐼 ∆ 𝑙𝑛 𝐼
0 2,6044 0,9093
0,0836 2,5928 0,9200
0,1595 2,5657 0,9541
0,1777 2,4479 1,0662
0,2612 2,3525 1,1585
0,3937 2,2058 1,3114
0,4773 2,0702 1,4399
0,5532 1,9843 1,5507
0,6209 1,9931 1,5245
y = -0,1021x + 2,664
R² = 0,967
0,0000
0,5000
1,0000
1,5000
2,0000
2,5000
3,0000
0 1 2 3 4 5 6 7 8
ln(I)
Espessura Pb (cm)

13. Onde 𝑦𝑖 é relativo aos pontos experimentais obtidos e 𝑦 𝑒𝑠𝑝𝑒𝑟𝑎𝑑𝑜 é referente aos valores
da reta de ajuste linear obtida usado o método dos mínimos quadrados.
O 𝜒2
normalizado foi de 1,57𝑥10−2
. Como 𝜒2
aproxima-se de zero podemos considerar
válida a regressão linear obtida.
Através do gráfico presente no guia laboratorial, é possível observar que para um fotão
de energia 𝐸 𝛾(𝐶é𝑠𝑖𝑜 − 137) = 661,7 𝑘𝑒𝑉 o valor para o comprimento de absorção máximo,
𝜆 𝑎𝑏𝑠 , é aproximadamente 9 𝑔/𝑐𝑚2
. Assim, pode-se concluir que o valor obtido
experimentalmente está de acordo com o esperado, apresentando um erro experimental de
10,5 %. Este erro relativo deve-se principalmente à dificuldade na colocação dos discos de
chumbo, que podem ter sofrido ligeiras modificações na sua posição o que levou à alteração dos
resultados relativos à taxa de contagem. Além disso, podem ter ocorrido erros sistemáticos
associados aos aparelhos de medição.