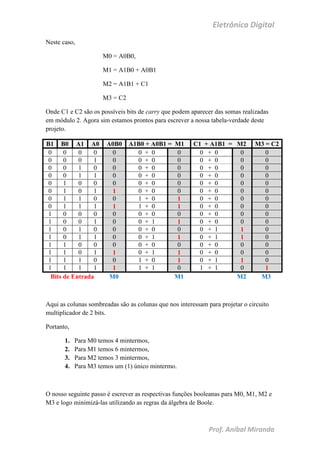
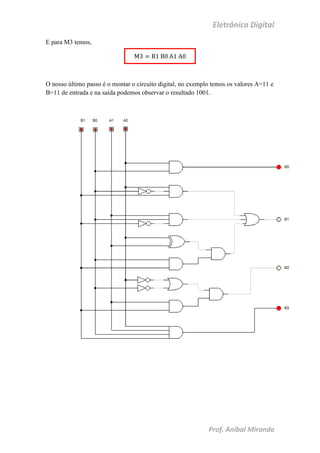
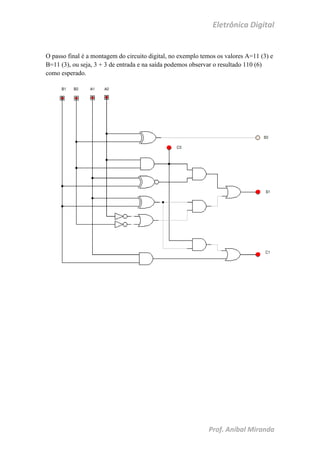
O documento apresenta a construção de circuitos digitais, incluindo um multiplicador e um somador de números binários de 2 bits, utilizando apenas álgebra booleana. Ele detalha a formação das funções booleanas necessárias e explica como montar as tabelas-verdade correspondentes, além de exemplificar a multiplicação de 3x3 e a soma de 11 + 11. O foco é na sua implementação prática e na simplificação das funções para o projeto dos circuitos.

1. Eletrônica Digital
Prof. Aníbal Miranda
Exemplos de Eletrônica Digital
Exemplo 1
Projetar um circuito multiplicador de números binários positivos de 2 bits cada um.
Utilizar somente as regras da álgebra Booleana (e não os Mapas de Karnaugh) para
encontrar o circuito resultante.
Sol.:
Como os números binários de entrada A e B são compostos cada um de 2 bits, então
trata-se de um circuito de 4 bits de entrada. Neste caso o maior valor dado por cada um
deles é o valor 3 em decimal ou 11 em binário, ou seja, 3x3 = 9, aqui observamos que 9
é um número decimal de 4 bits!
Portanto, o nosso circuito multiplicador de 2 bits deverá ter como máximo 4 linhas de
saída, ou seja,
Agora vamos analisar como as funções booleanas de saída M0, M1, M2 e M3 são
formadas. Para isto, vejamos através de um exemplo numérico, para o caso de A = 11 e
B = 11, fazendo a multiplicação temos,
Aqui os bits 1 (em vermelho) são os bit de carry devido às somas em módulo 2! Como
esperado o resultado de 3x3 é 9 (1001 binário).
Então no caso genérico de termos os dois números A (A1 A0) e B (B1 B0) ambos de 2
bits, temos o seguinte,
Circuito Multiplicador
Binário de
2 bits
A0
A1
B0
B1
M0 (LSB)
M1
M2
M3 (MSB)
A
B
1 1
X 1 1
1 1 1
+ 1 1 1 a
1 0 0 1
A1 A0
X B1 B0
C1 A1B0 A0B0
C2 A1B1 A0B1 a
M3 M2 M1 M0

2. Eletrônica Digital
Prof. Aníbal Miranda
Neste caso,
M0 = A0B0,
M1 = A1B0 + A0B1
M2 = A1B1 + C1
M3 = C2
Onde C1 e C2 são os possíveis bits de carry que podem aparecer das somas realizadas
em módulo 2. Agora sim estamos prontos para escrever a nossa tabela-verdade deste
projeto.
B1 B0 A1 A0 A0B0 A1B0 + A0B1 = M1 C1 + A1B1 = M2 M3 = C2
0 0 0 0 0 0 + 0 0 0 + 0 0 0
0 0 0 1 0 0 + 0 0 0 + 0 0 0
0 0 1 0 0 0 + 0 0 0 + 0 0 0
0 0 1 1 0 0 + 0 0 0 + 0 0 0
0 1 0 0 0 0 + 0 0 0 + 0 0 0
0 1 0 1 1 0 + 0 0 0 + 0 0 0
0 1 1 0 0 1 + 0 1 0 + 0 0 0
0 1 1 1 1 1 + 0 1 0 + 0 0 0
1 0 0 0 0 0 + 0 0 0 + 0 0 0
1 0 0 1 0 0 + 1 1 0 + 0 0 0
1 0 1 0 0 0 + 0 0 0 + 1 1 0
1 0 1 1 0 0 + 1 1 0 + 1 1 0
1 1 0 0 0 0 + 0 0 0 + 0 0 0
1 1 0 1 1 0 + 1 1 0 + 0 0 0
1 1 1 0 0 1 + 0 1 0 + 1 1 0
1 1 1 1 1 1 + 1 0 1 + 1 0 1
Bits de Entrada M0 M1 M2 M3
Aqui as colunas sombreadas são as colunas que nos interessam para projetar o circuito
multiplicador de 2 bits.
Portanto,
1. Para M0 temos 4 mintermos,
2. Para M1 temos 6 mintermos,
3. Para M2 temos 3 mintermos,
4. Para M3 temos um (1) único mintermo.
O nosso seguinte passo é escrever as respectivas funções booleanas para M0, M1, M2 e
M3 e logo minimizá-las utilizando as regras da álgebra de Boole.

3. Eletrônica Digital
Prof. Aníbal Miranda
No caso de M0 temos,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
Simplificando fica,
̅̅̅̅ (̅̅̅̅ ) (̅̅̅̅ )
̅̅̅̅
(̅̅̅̅ )
Finalmente
Agora a função booleana para M1 é dada pela soma de 6 mintermos,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ ̅̅̅̅
Fazendo as simplificações necessárias,
̅̅̅̅ (̅̅̅̅ ) ̅̅̅̅ ( ̅̅̅̅ ) (̅̅̅̅ ̅̅̅̅)
Portanto,
̅̅̅̅ ̅̅̅̅ ( )
Para M2 temos a função booleana,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
Simplificando fica,
̅̅̅̅ (̅̅̅̅ ) ̅̅̅̅
(̅̅̅̅ ̅̅̅̅)
Pela lei da Absorção,
(̅̅̅̅ ̅̅̅̅)

4. Eletrônica Digital
Prof. Aníbal Miranda
E para M3 temos,
O nosso último passo é o montar o circuito digital, no exemplo temos os valores A=11 e
B=11 de entrada e na saída podemos observar o resultado 1001.

5. Eletrônica Digital
Prof. Aníbal Miranda
Exemplo 2
Projetar um circuito somador de números binários de 2 bits cada. Utilizar somente as
regras da álgebra Booleana (e não os Mapas de Karnaugh) para encontrar o circuito
resultante.
Onde A0 A1 são os bits do número A e B0 B1 são os bits do número B, as saídas S0 e
C0 são as somas e o possível bit de carry respectivamente. Da mesma forma S1 e C1
são a soma e o bit de carry dessa segunda etapa do circuito.
Por exemplo, fazemos a soma dos números binários, A = 11 e B = 11,
Onde os bits em vermelho são os bits de carry C0 para a primeira soma e C1 para a
segunda soma, o resultado, como era de se esperar, é 110 (6 decimal).
Portanto, de forma genérica a soma de números binários de 2 bits é dada da seguinte
forma,
As saídas do circuito são,
S0 = B0 + A0
S1 = B1 + A1 + C0
C1 = C1
Meio Somador
Somador Completo
A0
B0
A1
B1
S0
C0
S1
C1
1 1
1 1
+ 1 1 1
1 1 0
C0 a
A1 A0
+ C1 B1 B0
C1 S1 S0

6. Eletrônica Digital
Prof. Aníbal Miranda
Agora passamos a fazer a tabela-verdade deste projeto de 4 bits de entrada (B1, B0, A1,
e A0).
B1 B0 A1 A0 B0 + A0 = S0 C0 + B1 + A1 = S1 C1
0 0 0 0 0 + 0 0 0 0 + 0 0 0
0 0 0 1 0 + 1 1 0 0 + 0 0 0
0 0 1 0 0 + 0 0 0 0 + 1 1 0
0 0 1 1 0 + 1 1 0 0 + 1 1 0
0 1 0 0 1 + 0 1 0 0 + 0 0 0
0 1 0 1 1 + 1 0 1 0 + 0 1 0
0 1 1 0 1 + 0 1 0 0 + 1 1 0
0 1 1 1 1 + 1 0 1 0 + 1 0 1
1 0 0 0 0 + 0 0 0 1 + 0 1 0
1 0 0 1 0 + 1 1 0 1 + 0 1 0
1 0 1 0 0 + 0 0 0 1 + 1 0 1
1 0 1 1 0 + 1 1 0 1 + 1 0 1
1 1 0 0 1 + 0 1 0 1 + 0 1 0
1 1 0 1 1 + 1 0 1 1 + 0 0 1
1 1 1 0 1 + 0 1 0 1 + 1 0 1
1 1 1 1 1 + 1 0 1 1 + 1 1 1
Bits de Entrada S0 C0 S1 C1
Dessa tabela verdade, as colunas que nos interessam apresentam as seguintes
características,
1. S0 tem 8 mintermos,
2. C0 tem 4 mintermos,
3. S1 tem 8 mintermos,
4. C1 tem 6 mintermos.
Portanto, a função boolena para S0 é dada por,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
Simplificando,
̅̅̅̅ ̅̅̅̅ (̅̅̅̅ ) ̅̅̅̅ ̅̅̅̅ (̅̅̅̅ ) ̅̅̅̅ (̅̅̅̅ )
̅̅̅̅ (̅̅̅̅ )
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ (̅̅̅̅ ̅̅̅̅) (̅̅̅̅ ̅̅̅̅)
̅̅̅̅ ( ) ( )

7. Eletrônica Digital
Prof. Aníbal Miranda
(̅̅̅̅ )( )
Finalmente,
( )
Agora encontramos a função booleana para o bit de carry C0,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ (̅̅̅̅ ) (̅̅̅̅ )
̅̅̅̅
(̅̅̅̅ )
Finalmente,
A função booleana para S1 é dada por 9 mintermos como mostrada embaixo,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
Simplificando e lembrando que o bit de carry , podemos escrever,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ ̅̅̅̅ (̅̅̅̅ ) (̅̅̅̅ ̅̅̅̅ ) ̅̅̅̅ ̅̅̅̅ (̅̅̅̅ )
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅ ̅̅̅̅ ( )̅̅̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
Do primeiro e o quarto termo fatoramos (̅̅̅̅ ) e do terceiro e quinto termos
fatoramos ( ̅̅̅̅)
̅̅̅̅ (̅̅̅̅ ̅̅̅̅) ( )̅̅̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ (̅̅̅̅ ̅̅̅̅ )

8. Eletrônica Digital
Prof. Aníbal Miranda
Agora temos que prestar muita atenção ao conteúdo entre parêntesis do primeiro e
terceiro termos.
Pela lei da Absorção temos que,
(̅̅̅̅ ̅̅̅̅) ̅̅̅̅ ̅̅̅̅
e
(̅̅̅̅ ̅̅̅̅ ) ̅̅̅̅ ̅̅̅̅
Portanto, com essas considerações podemos escrever,
̅̅̅̅ (̅̅̅̅ ̅̅̅̅) ( )̅̅̅̅̅̅̅̅̅̅̅̅̅̅ ̅̅̅̅ (̅̅̅̅ ̅̅̅̅)
Fatorado mais uma vez,
(̅̅̅̅ ̅̅̅̅)(̅̅̅̅ ̅̅̅̅ ) ( )̅̅̅̅̅̅̅̅̅̅̅̅̅̅
Finalmente,
(̅̅̅̅ ̅̅̅̅)( ) ( )̅̅̅̅̅̅̅̅̅̅̅̅̅̅
Agora encontramos a função booleana para o bit de carry C1, esta é dada por 6
mintermos,
̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅ ̅̅̅̅
̅̅̅̅
Fatorando elementos comuns do primeiro e quarto termo, assim como do segundo e
terceiro e do quinto e último para obter,
(̅̅̅̅ ̅̅̅̅) ̅̅̅̅ (̅̅̅̅ ) ( ̅̅̅̅ )
( ) ̅̅̅̅
( ) (̅̅̅̅ )
Finalmente,
( )

9. Eletrônica Digital
Prof. Aníbal Miranda
O passo final é a montagem do circuito digital, no exemplo temos os valores A=11 (3) e
B=11 (3), ou seja, 3 + 3 de entrada e na saída podemos observar o resultado 110 (6)
como esperado.