1. O documento discute circuitos aritméticos combinacionais, incluindo projeto de somadores, representação de números negativos e detecção de overflow.
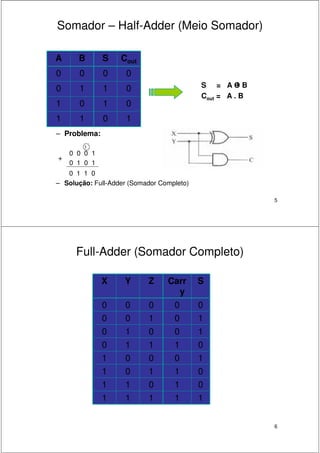
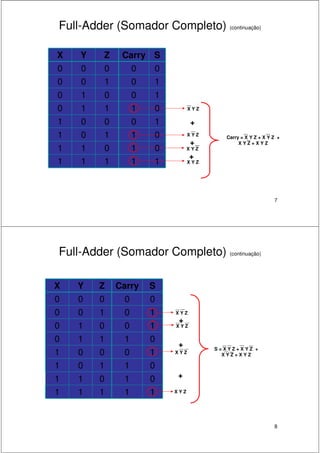
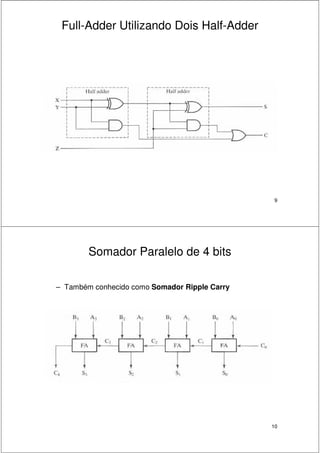
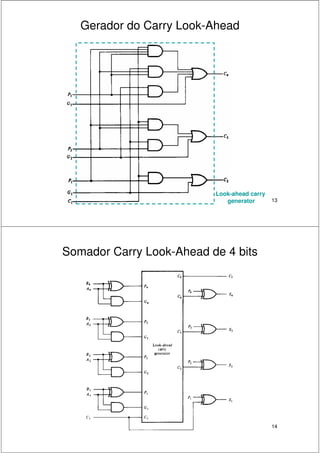
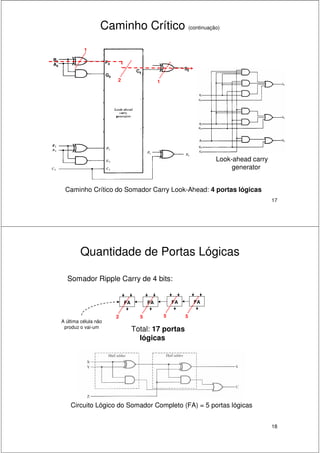
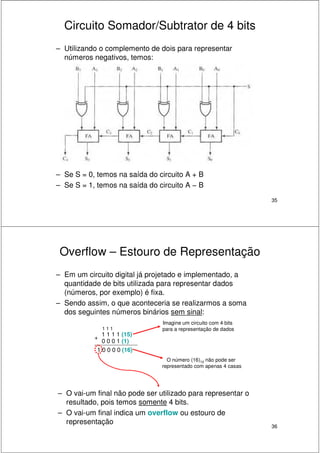
2. São descritos circuitos como somadores de meio-somador, somador completo, somador paralelo e somador com antecipação de carry.
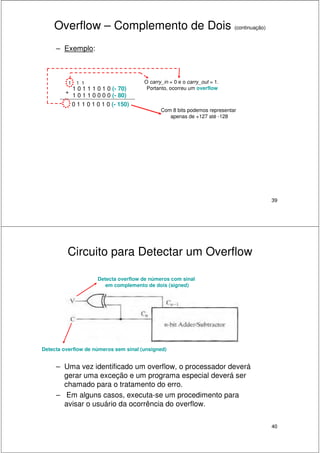
3. A representação de números negativos em complemento de dois é explicada e como permite realizar soma e subtração de forma similar.


















![53
Comparação Utilizando a Subtração (continuação)
– Sendo assim, temos:
• Resposta = M − N + 2n
• Se fizermos o complemento de dois da resposta, temos:
2n − [M − N + 2n] = 2n − 2n – M + N= N – M
– Se M < N, então não haverá produção de carry.
– Basta realizarmos o complemento de dois do resultado e
colocarmos um sinal de negativo (–) na frente do número
obtido
• Com isso, representamos o número em sinal-magnitude
Isso representa o valor absouto (magnitude)
do resultado
54
Comparação Utilizando a Subtração (continuação)
– Exemplo (X – Y):
• X = 1010100 (Número sem sinal)
• Y = 1000011 (Número sem sinal)
Y = 1 0 0 0 0 1 1
0 1 1 1 1 0 0 (Inverter os bits)
+
0 0 0 0 0 0 1 (Somar 1)
0 1 1 1 1 0 1 (complemento de dois de Y)
• Como houve vai-um final, então A > B.
– Descartamos o vai-um e assim obtemos a resposta correta: 0010001
1 0 1 0 1 0 0 (X)
Vai-um final
+
1 0 0 1 0 0 0 1
0 1 1 1 1 0 1 (complemento de dois de Y)
• Realizar a Soma:](https://image.slidesharecdn.com/circuitosaritmeticosalunos2-101023141716-phpapp02/85/Circuitos-aritmeticos-27-320.jpg)



