Curso mat financeira

JOÃO CANDIDO PEREIRA DE CASTRO NETO

CURSO DE MATEMÁTICA FINANCEIRA

CURITIBA – PR
2002

ÍNDICE

ÍNDICE........................................................................................................................................... I

LISTA DE TABELAS ................................................................................................................... III

1 INTRODUÇÃO.......................................................................................................................1

2 PERCENTAGENS..................................................................................................................2

2.1 ACRÉSCIMOS E ABATIMENTOS SOBRE PREÇOS INICIAIS E FINAIS .................................................2
2.2 ACRÉSCIMOS E ABATIMENTOS SUCESSIVOS ...........................................................................6

3 FUNDAMENTOS DA MATEMÁTICA FINANCEIRA .............................................................10

3.1 O PRINCÍPIO DA EQUIVALÊNCIA .........................................................................................10
3.2 AS TAXAS DE JUROS .......................................................................................................11
3.3 DIAGRAMA DE FLUXOS DE CAIXA .......................................................................................12

4 O REGIME DE CAPITALIZAÇÃO SIMPLES........................................................................13

4.1 JUROS SIMPLES .............................................................................................................13
4.2 MONTANTE SIMPLES .......................................................................................................14
4.3 TAXAS ..........................................................................................................................15
4.4 DESCONTOS SIMPLES .....................................................................................................15
4.4.1 Cálculo do Desconto Simples Comercial.................................................................16
4.4.2 Cálculo do Valor Atual Comercial............................................................................17

5 O REGIME DE CAPITALIZAÇÃO COMPOSTA...................................................................19

5.1 MONTANTE E JUROS DE UM ÚNICO PAGAMENTO ...................................................................19
5.2 DESCONTO ...................................................................................................................20
5.3 TAXAS DE JUROS COMPOSTOS ..........................................................................................20
5.4 TAXAS PROPORCIONAIS E EQUIVALENTES ............................................................................20
5.5 TAXAS NOMINAIS E EFETIVAS.............................................................................................21
5.6 REGIME DE CAPITALIZAÇÃO MISTA.....................................................................................22
5.7 EQUIVALÊNCIA DE FLUXOS DE CAIXA ..................................................................................23

6 SÉRIES UNIFORMES..........................................................................................................26

6.1 CLASSIFICAÇÃO, ELEMENTOS E CÁLCULOS ..........................................................................26
6.2 SÉRIES ANTECIPADAS .....................................................................................................26
6.3 SÉRIES IMEDIATAS ..........................................................................................................28
6.4 SÉRIES DIFERIDAS ..........................................................................................................29
6.5 SÉRIES GRADIENTES ......................................................................................................30

6.6 DECOMPOSIÇÃO DE FLUXOS DE CAIXA 32

Rua Luiz Leduc, 210 s. 03 i Fone /fax: 41 – 339 – 6270
82100 – 010 Curitiba – PR E-mail: jcandido@fesppr.br
http://www.fesppr.br/~candido

7 SISTEMAS DE FINANCIAMENTO.......................................................................................33

7.1 SISTEMA DO MONTANTE ..................................................................................................34
7.2 SISTEMA DO JURO ANTECIPADO (DESCONTOS) ...................................................................34
7.3 SISTEMA FRANCÊS OU SISTEMA PRICE ...............................................................................35
7.4 SISTEMA DE AMORTIZAÇÕES CONSTANTES .........................................................................36

8 ANÁLISE DE ALTERNATIVAS DE FINANCIAMENTO E INVESTIMENTO ..........................39

8.1 MÉTODOS DE ANÁLISE ....................................................................................................40
8.1.1 Método do Custo Anual .........................................................................................40
8.1.2 Método do Valor Presente Líquido .........................................................................45
8.1.3 Método da Taxa Interna de Retorno.......................................................................50
8.2 CLASSIFICAÇÃO DE ALTERNATIVAS ....................................................................................53
8.2.1 Alternativas Singulares...........................................................................................53
8.2.2 Alternativas Múltiplas .............................................................................................53
8.2.3 Alternativas com Vidas Econômicas Diferentes ......................................................54

ANEXOS......................................................................................................................................55

BIBLIOGRAFIA ...........................................................................................................................62

Rua Luiz Leduc, 210 s. 03 ii Fone /fax: 41 – 339 – 6270

LISTA DE TABELAS

VALOR PRESENTE DE UM PAGAMENTO .................................................................................56

VALOR FUTURO DE UM PAGAMENTO .....................................................................................57

VALOR PRESENTE DE UMA SÉRIE UNIFORME IMEDIATA......................................................58

VALOR FUTURO DE UMA SÉRIE UNIFORME IMEDIATA..........................................................59

FATOR DE CONVERSÃO DE SÉRIE GRADIENTE PARA IMEDIATA .........................................60

TABELA PARA CONTAGEM DE DIAS ENTRE DATAS ..............................................................61

Rua Luiz Leduc, 210 s. 03 iii Fone /fax: 41 – 339 – 6270

1

1. Introdução

Tornou-se lugar comum afirmar que, no Brasil, a grande maioria das
empresas fecha suas portas ao final dos cinco primeiros anos de operação e parece
ser consenso entre professores, consultores e administradores que as dificuldades
na obtenção e administração do capital de giro respondem pela quase totalidade
dessas baixas.
Sabe-se, também, que a maior parte do tempo destinado à administração
das empresas brasileiras é dedicada à administração financeira. De fato, o ambiente
econômico e financeiro nacional não perdoa os amadores. Altos níveis de
concentração de renda, taxas de juros estratosféricas e carga tributária extorsiva
constituem entraves seriíssimos à atividade econômica que tornam o dia a dia da
gestão empresarial um desafio gigantesco.
Nesse contexto, o conhecimento da matemática comercial e financeira,
mais que nunca, é fundamental para a administração nas mais diversas áreas.
Do cálculo das comissões de vendas, à avaliação de projetos alternativos
de investimento, buscou-se, neste trabalho, apresentar as poderosas ferramentas
da matemática comercial e financeira com uma preocupação permanente com a
linguagem acessível e com a sua utilidade prática. Sempre que possível, buscou-se
utilizar uma nomenclatura idêntica à das calculadoras financeiras, de modo a
facilitar a compreensão e o uso daqueles instrumentos.
Nos anexos apresentam-se tabelas de índices que têm o objetivo de
possibilitar cálculos rápidos para algumas taxas e prazos e, ainda, uma tabela
prática para cálculo de prazos entre datas.
Espera-se oferecer um instrumento de aprendizado e consulta que possa
auxiliar nossos alunos e treinandos na ampliação e consolidação de seus
conhecimentos e na sua evolução profissional.

Rua Luiz Leduc, 210 s. 03 Fone /fax: 41 – 339 – 6270

2

2. Percentagens

Uma percentagem é um número relativo, que pode ser utilizado para
comparar grandezas de qualquer espécie: volume, área, peso, etc.
A percentagem (r) representa parte (p) de uma grandeza que foi dividida
em cem unidades, que chamamos de principal (P).
Fazendo uma regra de três, temos:
P p P×r r
= p= = P× p = P×i
100 r 100 100
Onde i é uma taxa e é igual à percentagem dividida por cem:
r
i=
100
Exemplo: Calcular 8% de 560.
Comentário: Podemos calcular utilizando a percentagem ou a taxa.
560 × 8
p= = 44,8
100
ou
p = 560 × 0,08 = 44,8

2.1 Acréscimos e abatimentos

O valor resultante de um acréscimo é chamado de valor bruto (B) e é igual
ao principal mais a parte que foi acrescida.
B = P+ p
Nós já vimos que a parte é igual ao principal multiplicado pela taxa:
p = P×i
Substituindo na equação anterior, temos:
B = P + P×i
ou
B = P × (1 + i )
Da mesma forma, ao fazermos um abatimento, o valor resultante é o valor
líquido (L), que é igual ao principal menos a parte que foi abatida.


3

L = P− p
Como:
p = P×i
Substituindo na equação anterior:
L = P − P×i
ou
L = P × (1 − i )

2.2 Operações com mercadorias

Nos acréscimos como nos abatimentos, podemos considerar como
principal tanto o preço inicial (Po), que é o preço antes da operação ou preço de
custo, como o preço final (Pn) que é o preço depois da operação ou preço de venda.
Isso costuma gerar muita confusão, pois um mesmo acréscimo ou
abatimento pode ser representado por duas percentagens, uma calculada "sobre" o
preço inicial e outra calculada "sobre" o preço final.
Assim, se o principal é o preço inicial, o que é mais comum, em um
acréscimo o preço final é um valor bruto igual ao preço inicial mais o acréscimo:
B = P × (1 + i ) Pn = P0 × (1 + i0 )

Em um abatimento, o preço final é um valor líquido igual ao preço inicial
menos o abatimento:
L = P × (1 − i ) Pn = P0 × (1 − i0 )

Porém, em certas ocasiões como no cálculo do ICMS, por exemplo, o
principal é o preço final, isto é, o cálculo é feito sobre o preço que já inclui a
operação. Nesse caso, em um acréscimo, o preço inicial é um valor líquido igual ao
preço final menos o acréscimo:
L = P × (1 − i ) P0 = Pn × (1 − in )

ou
P0
Pn =
(1 − in )

Em um abatimento, o preço inicial é um valor bruto igual ao preço final
mais o abatimento:


4

B = P × (1 + i ) P0 = Pn × (1 + in )

ou
P0
Pn =
(1 + in )


5

EXERCÍCIOS

1) Quanto é 8% de 1.253.897,33?
2) Quanto por cento 1.200 é de 8.000?
3) 1.000,00 são 3% de quanto?
4) A cotação da libra esterlina passou de R$ 1,86 para R$ 1,90. Qual foi a variação percentual?
5) A saca de café passou de US$ 40,00 para US$ 30,00. Qual foi a variação percentual?
6) A saca de café passou de R$ 75,00 para R$ 100,00. Qual foi a variação percentual?
7) O preço de venda de certa mercadoria representa um acréscimo de 15% sobre o preço de custo
de R$ 5.800,00. Qual é o preço de venda?
8) O preço de venda de certa mercadoria é R$ 1.500,00 e representa um acréscimo de 25% sobre o
preço de custo. Calcule o preço de custo.
9) O preço de venda de certa mercadoria é de R$ 6.700,00, o que inclui uma margem que representa
25% desse preço de venda. Calcule o preço de custo.
10) O preço de custo de certa mercadoria é de R$ 8.000,00, o que permite vendê-la com uma
margem que representa 20% do preço de venda. Calcule esse preço de venda.
11) Uma mercadoria que custou R$ 12.000,00 foi vendida por R$ 16.000,00. Qual foi a margem
sobre o preço de custo? Qual sobre o de venda?
12) O preço de venda de certa mercadoria é R$ 1.500,00 e resulta de um abatimento de 25% sobre o
preço de custo. Calcule o preço de custo.
13) Uma mercadoria custou R$ 9.000,00, o que obriga a vendê-la com um prejuízo de 30% sobre o
preço de custo. Calcular o preço de venda.
14) O preço de venda de certa mercadoria é de R$ 6.700,00 e resulta de um desconto de 25% sobre
a venda. Calcule o preço de custo.
15) O preço de custo de certa mercadoria é de R$ 8.000,00, o que obriga a vendê-la com um
prejuízo que representa 20% do preço de venda. Calcule esse preço de venda.

RESPOSTAS:

1) 100.311,79 2) 15% 3) 33.333,33 4) 2,15% 5) - 25% 6) 33,33% 7) R$ 6.670,00 8) R$ 1.200,00 9) R$
5.025,00 10) R$ 10.000,00 11) 33,33% e 25% 12) R$ 2.000,00 13) R$ 6.300,00 14) R$ 8.375,00 15)
R$ 6.666,67


6

2.3 Acréscimos e abatimentos sucessivos

Os acréscimos e abatimentos podem ser feitos de forma sucessiva. Isso
quer dizer que, em uma série de Operações, cada operação é realizada de forma
acumulada, "sobre" o resultado da operação anterior. Dessa forma, o bruto de cada
acréscimo ou o líquido de cada abatimento passa a ser o principal da operação
seguinte.
Vamos imaginar uma série de acréscimos feitos de forma sucessiva, a
partir de um principal. O bruto do primeiro acréscimo seria calculado por:
B1 = P × (1 + i1 )
O do segundo, por:
B2 = B1 × (1 + i 2 ) = P × (1 + i1 ) × (1 + i2 )
O terceiro, por:
B3 = B2 × (1 + i3 ) = P × (1 + i1 ) × (1 + i2 ) × (1 + i3 )

E assim por diante. Sendo n uma quantidade qualquer de acréscimos,
poderíamos escrever que:
Bn = P × (1 + i1 ) × (1 + i2 ) × ... × (1 + in )

E se fossem vários acréscimos iguais, teríamos:
Bn = P × (1 + i ) × (1 + i ) × ... × (1 + i ) Bn = P × (1 + i ) n

Como esses acréscimos são realizados sobre principais diferentes, o
acréscimo total é sempre diferente do (maior que o) obtido pela simples soma das
taxas. Isto nos leva à busca de uma taxa única que corresponda à aplicação de
diversas taxas de forma sucessiva. Assim, o valor bruto produzido por essa taxa
única de acréscimos (iua) será igual ao valor bruto produzido pelas diversas taxas de
acréscimos sucessivos:
Bu = B n

sendo:
Bu = P × (1 + iua ) e Bn = P × (1 + i1 ) × (1 + i2 ) × ... × (1 + in )

assim,


7

P × (1 + iua ) = P × (1 + i1 ) × (1 + i2 ) × ... × (1 + in )

1 + iua = (1 + i1 ) × (1 + i 2 ) × ... × (1 + in )

e, finalmente:
iua = (1 + i1 ) × (1 + i2 ) × ... × (1 + in ) − 1

Se fossem vários acréscimos iguais, teríamos:
iua = (1 + i) × (1 + i) × ... × (1 + i) − 1 iua = (1 + i ) n − 1

Vamos imaginar, agora, uma série de abatimentos feitos de forma
sucessiva, a partir de um principal. O líquido do primeiro abatimento seria:
L1 = P × (1 − i1 )
O do segundo, por:
L2 = L1 × (1 − i 2 ) = P × (1 − i1 ) × (1 − i2 )
O terceiro, por:
L3 = L2 × (1 − i3 ) = P × (1 − i1 ) × (1 − i2 ) × (1 − i3 )

E assim por diante. Sendo n uma quantidade qualquer de abatimentos,
poderíamos escrever que:
Ln = P × (1 − i1 ) × (1 − i2 ) × ... × (1 − i n )

E se fossem vários abatimentos iguais, teríamos:
Ln = P × (1 − i) × (1 − i) × ... × (1 − i ) Ln = P × (1 − i ) n

Como os abatimentos sucessivos resultam em um abatimento total
diferente da (menor que a) soma das taxas de abatimento, podemos calcular a taxa
única que corresponde à aplicação de diversas taxas de abatimento sucessivas. O
valor líquido produzido por essa taxa única de abatimentos, ou taxa única de
descontos (iud) será igual ao valor líquido produzido pelas diversas taxas de
abatimentos sucessivos:
Lu = Ln

sendo:
Lu = P × (1 − iud )

e
Ln = P × (1 − i1 ) × (1 − i2 ) × ... × (1 − i n )


8

Assim,
P × (1 − iud ) = P × (1 − i1 ) × (1 − i2 ) × ... × (1 − i n )

1 − iud = (1 − i1 ) × (1 − i 2 ) × ... × (1 − in )

− iud = (1 − i1 ) × (1 − i 2 ) × ... × (1 − i n ) − 1

E, finalmente:
iud = 1 − (1 − i1 ) × (1 − i 2 ) × ... × (1 − in )

E, se fossem vários abatimentos iguais, teríamos:
iud = 1 − (1 − i) × (1 − i) × ... × (1 − i ) iud = 1 − (1 − i) n


9

EXERCÍCIOS

1) Calcular o valor bruto de uma mercadoria cujo preço de fábrica é de R$ 1.200,00 por unidade e
que sofre os acréscimos sucessivos de 3%, 5% e 7%.
2) Calcular o valor inicial de uma mercadoria que sofreu, de forma sucessiva, os acréscimos de 5%,
10%, 15% e 20% e foi vendida por R$ 150.000,00.
3) Calcular o valor líquido de uma mercadoria que sofreu, sucessivamente, os abatimentos de 5%,
10%, 15% e 20% sobre o valor inicial de R$ 100.000,00.
4) Calcular o valor inicial de uma mercadoria que foi vendida por R$ 50.000,00 após sofrer os
abatimentos sucessivos de 10%, 20%, 30% e 40%.
5) Qual a taxa única que corresponde aos acréscimos de 5%, 10%, 15% e 20% aplicados de forma
sucessiva?
6) Qual a taxa única que corresponde aos abatimentos de 5%, 10%, 15% e 20% aplicados de forma
sucessiva?
7) Uma mercadoria cujo preço de fábrica é de R$ 15.000,00 sofre, de forma sucessiva, os
acréscimos de 3%, 5%, 8% e um quarto que eleva o seu preço final a R$ 21.024,36. Qual a
percentagem do o último acréscimo?
8) Ao comprar certa mercadoria por R$ 20.000,00, obtive os descontos de 15%, 20% e um terceiro.
Os descontos foram realizados de forma sucessiva, sobre o preço da etiqueta de R$ 42.016,81. Qual
a percentagem do último desconto?
9) O acréscimo total de 27,63% foi resultante da aplicação de cinco taxas iguais de forma sucessiva.
Qual a percentagem dessas taxas?
10) O abatimento total de 22,62% foi resultante da aplicação de cinco taxas iguais de forma
sucessiva. Qual a percentagem dessas taxas?

RESPOSTAS:

1) R$ 1.388,65 2) R$ 94.108,79 3) R$ 58.140,00 4) R$ 165.343,92 5) 59,39% 6) 41,86% 7) 20,00% 8)
30,00% 9) 5,00% 10) 5,00%


10

3. Fundamentos da Matemática Financeira

3.1 O Princípio da Equivalência

O princípio fundamental da Matemática Financeira é o princípio da
equivalência. O princípio da equivalência baseia-se no fato de que o dinheiro muda
de valor no decorrer do tempo. Assim, uma determinada quantia teria significados
econômicos diferentes em épocas diferentes, ainda que em ambiente não
inflacionário. A partir desse raciocínio, podemos imaginar uma outra quantia,
situada em época futura, que tenha o mesmo significado econômico, o mesmo valor,
que certa quantia conhecida no presente. Em outras palavras, um Valor Futuro (FV)
equivalente ao Valor Presente (PV) conhecido. Da mesma forma, podemos imaginar
que exista, no presente, uma quantia com o mesmo valor que outra quantia
conhecida no futuro, ou prevista. Em outras palavras, um Valor Presente
equivalente ao Valor Futuro conhecido ou previsto.
A diferença entre o Valor Presente e o Valor Futuro é a parcela
correspondente aos juros (j). Os juros podem ser definidos livremente como o
aluguel do capital. Existem várias justificativas para os juros. Entre elas podemos
citar a teoria da produtividade marginal do capital: o capital, associado aos outros
fatores de produção, é, também produtivo. Como o capital é, então, um dos fatores
de produção, os juros correspondem à remuneração do fator capital, da mesma
forma, por exemplo, que os salários remuneram o fator trabalho. Outra teoria é a do
preço do tempo ou abstinência de Böhm-Bawerk (escola psicológica austríaca) que
diz que um capital emprestado é um bem presente que se dá em troca de um bem
futuro. Como a expectativa de um bem futuro vale menos que a realidade do bem
presente, os juros compensariam essa diferença. Assim, o Valor Futuro é o
resultado da soma do Valor Presente com a sua remuneração sob a forma de juros:

FV = PV + j


11

3.2 As Taxas de Juros

O nível de preços dos bens e serviços é função de sua escassez. Da
mesma maneira que as forças de oferta e demanda determinam o preço dos bens e
serviços, as forças de oferta de fundos e a procura de crédito determinam o preço
do crédito que é representado pela taxa de juros. Na verdade, essas forças de
mercado determinam o nível (i0) da taxa de juros pura (ip), correspondente a uma
situação de virtual equilíbrio de mercado decorrente da quantidade (Q0) de recursos
demandados (Q).

ip

D S

io

Q0 Q

O mercado adiciona, a essa taxa pura, um conjunto de outras taxas
(spread) que visam cobrir impostos (IOF), comissões (flat) e custos de
intermediação financeira e uma taxa correspondente à remuneração do fator risco
(iρ), que é variável e visa remunerar o risco específico daquele tipo de operação. O
resultado é a taxa real (ir) de juros, que corresponde ao custo real das operações
financeiras. Assim, a taxa real é:

ir = ip + IOF + flat + custos + iρ


12

ir

ir0

iρ

ip + flat + IOF + custos

ρ0 ρ

À taxa real pode, então, ser acumulada a expectativa de inflação (iη) para
constituir a taxa efetiva (ie) de juros, como a seguir:

ie = (1 + ir) . (1 + iη) - 1

Observe que a taxa de inflação acumula-se à taxa real de juros, como nos
acréscimos sucessivos (2.3), para formar a taxa efetiva. Não basta, portanto,
somar a taxa de inflação à taxa de juros, pois os juros incidem sobre o capital já
corrigido monetariamente, i. e., já compensado pelo desgaste da inflação.

3.3 Diagrama de Fluxos de Caixa

O Diagrama de Fluxos de Caixa (DFC) é a representação gráfica das
operações financeiras. Como o valor de um fluxo de caixa (pagamento ou
recebimento) é função do tempo, necessita ser representado em uma escala
cronológica que o situe exatamente na época de sua ocorrência. Assim, o DFC é
constituído de um segmento de reta graduado de forma a representar os intervalos
de tempo entre os fluxos. Estes são representados por vetores verticais orientados
para cima (recebimentos - fluxos positivos) ou para baixo (pagamentos - fluxos


13

negativos) com origem na escala cronológica, na graduação correspondente à
época de ocorrência. Um Diagrama de Fluxos de Caixa pode ter o seguinte aspecto:

200 200

100 100 100

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

50
100 100
150
200

4. O Regime de Capitalização Simples

4.1 Juros Simples

Juro é o prêmio que se paga pela utilização de um capital por certo tempo.
A capitalização simples é um regime de cálculo de juros (j) em que estes
são definidos, em cada período, como uma parte de um mesmo principal. Este
principal é o capital (C) da operação financeira. Os juros são, então, obtidos pela
aplicação de uma percentagem ou taxa, a taxa de juros (i) sobre este principal.
Como sabemos,

p=P.i

Logo,

j=C.i


14

Para obter o total de juros produzidos em certo número de períodos (n),
fazemos:

j=C.i.n

Exemplo: Calcular os juros simples do capital de R$ 1000,00, a 15% a.a.,
em cinco meses.
Comentário: Para todo o cálculo financeiro, é fundamental que o prazo e a
taxa de juros estejam se referindo ao mesmo período de capitalização. No exemplo
acima, temos uma taxa ao ano (a.a.) e um prazo expresso em meses. No entanto,
esse prazo pode ser expresso como uma fração do período de capitalização anual:

C = 100 j = C.i.n
5
i = 0,15a.a. j = 1000.0,15.
12
5
n = 5me = a j = R$62,50
12

4.2 Montante Simples

Montante Simples (M) é o resultado da soma do capital com os juros.
Portanto,
M=C+j
Como vimos anteriormente,
j=C.i.n
Logo,
M = C + C. i. n
ou
M = C . ( 1 + i . n)

Exemplo: Calcular o montante de um capital de R$ 700,00, a 10% a.me.,
em 6 meses.


15

Comentário: Nesse caso, a taxa e o prazo já se referem ao mesmo período
de capitalização (um mês). Podemos, portanto, aplicar a fórmula diretamente:
C = 700 M = C .(1 + i.n)
i = 0,10a.me. M = 700.(1 + 0,10.6)
n = 6me M = R$1.120, 00

4.3 Taxas

As taxas de juros podem ser classificadas em proporcionais e
equivalentes.
Taxas proporcionais são aquelas que se relacionam com os prazos a que
se referem formando uma proporção. Assim, a taxa de 24% ao ano é proporcional a
12 % ao semestre, a 2% ao mês, etc.
Taxas equivalentes são aquelas que produzem o mesmo resultado quando
aplicadas pelo mesmo prazo. No Regime de Capitalização Simples, as taxas
proporcionais são equivalentes.
Assim, se aplicarmos um capital a 5% ao mês durante dois anos, iremos
obter a mesma quantidade de juros que obteríamos aplicando por dois anos esse
capital a 10 % ao bimestre, a 30% ao semestre ou a 60% ao ano.
A matemática financeira utiliza duas convenções para contagem do prazo
das operações financeiras (período financeiro): o ano comercial, com 360 dias e,
portanto, 12 meses com 30 dias cada, e o ano civil, com 365 ou 366 dias quando
bissexto e com os 12 meses com a respectiva quantidade de dias. Em geral, quando
o contrato não especifica se é juro comercial ou juro civil, utiliza-se a convenção
comercial por maior facilidade. No entanto, quando o contrato especifica o contrário,
ou quando o prazo é estabelecido entre duas datas, utiliza-se o ano civil. Para a
contagem de dias entre duas datas, ver a Tabela nº 4.2 - p.59 .

4.4 Descontos Simples

A operação de desconto é inversa à da capitalização e consiste em se
determinar um Valor Presente equivalente a um determinado Valor Futuro. Em
termos práticos, as operações de desconto são realizadas com os títulos de crédito
que são os instrumentos de crédito que possuem garantia legal (duplicatas, notas


16

promissórias, etc.). Possuindo garantia legal, esses títulos podem ser negociados
livremente, antes de sua data de vencimento. Assim, um título de crédito pode ser
convertido em dinheiro ou substituído por outro(s) título(s) anteriormente à data
prevista para sua liquidação. A conversão é feita pelo Valor Atual (An) ou Valor
Presente do título, que corresponde ao Valor de Face, Valor Nominal (N) ou Valor
Futuro do título, menos o desconto (d) que é a compensação em valor pela
antecipação do resgate do título.
O Regime de Capitalização Simples utiliza duas formas de cálculo para o
desconto: o Desconto Simples Comercial e o Desconto Simples Racional. Como
apenas a modalidade comercial é praticada, ainda que sua utilização seja restrita a
operações de curto prazo, nos ateremos ao seu estudo.

4.4.1 Cálculo do Desconto Simples Comercial

O Desconto Simples Comercial (dc), também chamado Desconto Simples
"Por Fora", equivale aos juros simples calculados sobre o Valor Nominal (F) do
título. Da fórmula dos juros simples:
j=C.i.n

Tiramos, substituindo j por dc e C por N,
dc = N . i . n

Exemplo: Calcular o desconto comercial de um título de R$ 500,00,
descontado 27 dias antes do vencimento, à taxa de desconto de 5% ao mês.
Comentário: Como o prazo não está em uma unidade de tempo compatível
com o período de capitalização da taxa, é necessário expressá-lo em função dessa
nova unidade de tempo.
N = 500 dc = N .i.n
27
i = 0, 05a.me. dc = 500.0, 05.
30
27
n = 27 d = me d c = R$22, 50
30


17

4.4.2 Cálculo do Valor Atual Comercial

O Valor Atual é o valor pelo qual o título é resgatado ou negociado antes
do seu vencimento e corresponde à diferença entre o Valor Nominal e o Desconto:
Anc = N - dc

Porém, como
dc = N . i . n,

podemos escrever:
Anc = N - N . i . n => Anc = N (1 - i . n)

Exemplo: Calcular o Valor de Resgate de um título de R$ 1100,00, 25 dias
antes do seu vencimento, à taxa de desconto de 8% a.me.
Comentário: O exemplo não especifica a modalidade de desconto simples
utilizada. Sendo assim, como norma, utilizamos o desconto comercial.

N = 1100 Anc = N (1 − i.n)
25
i = 0, 08a.me. Anc = 1100.(1 − 0, 08. )
30
25
n = 25d = me Anc = R$1.026, 67
30


18

EXERCÍCIOS
1) Calcular os juros simples do capital de R$ 1.000,00 durante 19 dias 16% ao mês.
2) Calcular o montante a juros simples do capital de R$ 2.500,00, durante 23 dias, a 14% ao mês.
3) Ao fim de quanto tempo o capital de R$ 5.000,00 a 20% a.a. produzirá juros simples de R$
1.500,00?
4) Ao fim de quanto tempo o capital de R$ 2.500,00 a 10% ao ano produzirá o montante a juros
simples de R$3.250,00?
5) Um investidor aplicou R$ 250.000,00 em Letras de Câmbio no dia 15 de janeiro de 1995 e, ao
resgatá-las no dia 16 de março do mesmo ano, recebeu R$ 320.500,00. Quanto recebeu de juros?
Que taxa mensal remunerou seu capital nesse período?
6) Um empresário pediu um empréstimo de R$ 25.000,00 a uma instituição financeira, por certo
período. Na liberação do empréstimo, pagou antecipadamente, como previa o contrato, 22% de
juros. Qual o valor pago de juros? Qual a quantia efetivamente liberada? Considerando a quantia
liberada como empréstimo, qual foi a taxa efetiva de juros?
7) Um título foi descontado, 47 dias antes de seu vencimento, à taxa de 7% a.me., por R$ 4.451,67.
Calcular o Valor Nominal do título.
8) Uma nota promissória de R$ 7.500,00 foi resgatada, dois meses antes de seu vencimento, por R$
5.250,00. Calcular a taxa de desconto.
9) Uma empresa descontou em um banco, no dia 26 de maio, três títulos de R$ 20.000,00; R$
15.000,00 e R$35.000,00, vencíveis, respectivamente, em 27 de junho, 28 de julho e 24 de agosto
do mesmo ano. Calcule o valor atual utilizando a taxa de desconto de 15% a.me.
10) Uma empresa devedora de três títulos de R$ 2.000,00; R$ 1.500,00 e R$ 3.000,00, vencíveis em
32, 63 e 90 dias, respectivamente, propõe ao banco credor substituí-los por dois outros, de mesmo
valor nominal, para 40 e 75 dias. Calcule o valor nominal desses títulos a uma taxa de desconto de
15% ao mês.

RESPOSTAS:

1) R$ 101,33 2) R$ 268,33 3) 1a6me 4) 3a 5) R$ 70 500,00; 14,10% a.me. 6) R$ 5.500,00; R$
19.500,00; 28,21% 7) R$ 5.000,00 8) 15% a.me. 9) R$ 46.325,00 10) R$ 3.057,89


19

5. O Regime de Capitalização Composta

5.1 Montante e juros de um único pagamento

No Regime de Capitalização Composta, os juros são sempre calculados
sobre o valor bruto do período anterior. Ao contrário do que ocorre no Regime de
Capitalização Simples, no qual temos sempre o mesmo principal, neste regime o
principal muda a cada período de capitalização. O principal é sempre o Montante ou
Valor Futuro (FV) do período anterior.
É claro que para o primeiro período não temos montante do período
anterior. Assim, os juros compostos do primeiro período são iguais aos juros
simples, se usarmos a mesma taxa e o mesmo capital e, claro, o montante também
é o mesmo.
Partindo de um certo Capital Inicial (PV), os juros do primeiro período
seriam, como em juros simples:

j = PV . i

e o montante seria:
FV1 = PV . (1 + i . 1) = PV . (1 + i)

O montante do segundo período seria:
FV2 = FV1 . (1 + i) = PV . (1 + i) . (1 + i) = PV . (1 + i)2

O montante do terceiro período seria:
2 3
FV3 = FV2 . (1 + i) = PV . (1 + i) . (1 + i) = PV . (1 + i)

E assim por diante, o que nos permite generalizar assim:
FV = PV. (1 + i)n
(Ver Tabela 2 - p.64)


20

Ao trabalhar com juros compostos, é mais simples obter o montante e
depois subtrair o capital inicial para obter o valor dos juros. Assim:
j = FV - PV
j = PV . (1 + i)n - PV

e, finalmente,
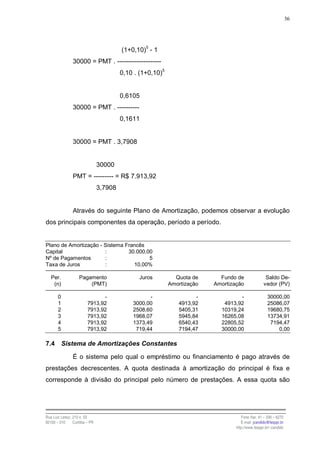
j = PV . [(1 + i)n - 1]

5.2 Desconto

O desconto é a operação inversa da capitalização. Enquanto a operação
de capitalização agrega, a cada período, os juros ao capital inicial ou Valor
Presente para produzir o montante ou Valor Futuro, a operação de desconto retira,
a cada período, os juros de um determinado Valor Futuro para produzir o Valor
Presente daquele período.
Usando a fórmula do montante, basta isolarmos no primeiro membro o
Valor Presente:
FV = PV . (1 + I)n => PV = FV . (1 + i)-n
(Ver Tabela 1 - p. 63)

5.3 Taxas de juros compostos

5.4 Taxas proporcionais e equivalentes

A exemplo do que vimos em juros simples, as taxas podem ser
classificadas em proporcionais e equivalentes. Porém, ao contrário do que ocorre
nos juros simples, no Regime de Capitalização Composta as taxas proporcionais
não são equivalentes. Isso ocorre porque, nesse regime, os juros não são
calculados sempre sobre o mesmo principal, mas sim sobre o montante do período
anterior. Como as taxas incidem, a cada período, sobre um principal diferente, a
taxa equivalente ao fim de um certo número de períodos não pode ser
simplesmente o resultado do produto da taxa ao período pelo número de períodos,
como uma taxa proporcional.


21

Usando a fórmula do valor futuro e um valor presente igual a um, vamos
imaginar uma taxa (iq) que produza, no mesmo prazo, o mesmo montante em um
número de períodos (1/q) que outra taxa (it) produziria em outro número de períodos
(1/t). As fórmulas ficariam assim:
FV = PV. (1 + iq)1/q
FV = PV . (1 + it)1/t

Como ambas dão como resultado o mesmo FV, podemos igualá-las:
PV . (1 + iq)1/q = PV . (1 + it)1/t

e, simplificando PV, temos:
1/q 1/t
(1 + iq) = (1 + it)
1 + iq = (1 + it)q/t
iq = (1 + it)q/t - 1
Para facilidade de aplicação, podemos ler esta fórmula desta forma pouco
ortodoxa: "A taxa que queremos (iq) é igual a 1 mais a taxa que temos (it), elevado
ao número de capitalizações que queremos (q), em um certo prazo, dividido pelo
número de capitalizações que temos (t), no mesmo prazo, menos 1." P. Ex. calcular
a taxa anual equivalente a 2% a.m..
it = 2% a.m. (a taxa que temos)
t = 1 (número de capitalizações que temos – 1 mês)
q = 12 (número de capitalizações que queremos – 12 meses)
iq = (1 + it)q/t – 1
iq = (1 + 0,02)12/1 – 1
iq = 1,0212 – 1
iq = 1,2682 – 1
iq = 0,2682 = 26,82% a.a.

5.5 Taxas nominais e efetivas

É comum que os contratos financeiros apresentem a taxa de juros relativa
a um período de tempo (geralmente ao ano), chamado de período financeiro, mas


22

que os cálculos considerem a incidência dos juros em um período diferente
(geralmente ao mês), chamado de período de capitalização. O cálculo, nesses
casos, é feito com a utilização da taxa no período de capitalização proporcional à
taxa contratada no período financeiro. P. Ex. 10% a.a. capitalizados mensalmente:

taxa contratada: 10% a.a. período financeiro: um ano
capitalização: mensal período de capitalização: um mês
taxa proporcional no período de capitalização: 10% ÷ 12 = 0,83% a.m.

Sabemos, no entanto, que, por se tratar do regime de capitalização
composta, o resultado obtido será diferente do resultado indicado pela taxa
contratada. Assim, a taxa contratada de 10% a.a. é apenas uma taxa anual
proporcional à taxa no período de capitalização, é uma taxa meramente nominal,
pois não corresponde ao resultado da operação.
A taxa que realmente reflete o custo financeiro anual da operação é a taxa
anual equivalente a 0,83% a.m.. Já vimos como calculá-la:
iq = (1 + it)q/t – 1
iq = (1 + 0,0083)12/1 – 1
iq = 1,008312 – 1
iq = 1,1043 – 1
iq = 0,1043 = 10,43% a.a.
Esta taxa de 10,43% a.a. é a taxa efetiva da operação e corresponde ao
custo anual da operação, diferentemente da taxa nominal de 10% a.a..

5.6 Regime de Capitalização Mista

Já pudemos verificar que o montante gerado pelo Regime de
Capitalização Composta é maior que o gerado pelo Regime de Capitalização
Simples. Porém, isso só ocorre para um número inteiro de períodos. Quando o
prazo é uma quantidade não inteira de períodos de capitalização, o montante
gerado na parte fracionária do prazo, e apenas nessa parte fracionária, será maior
se for calculado a juros simples. Assim, o mercado adota a Convenção Linear, que


23

calcula o montante a juros compostos pela parte inteira de períodos de capitalização
de um prazo, e o montante desse resultado a juros simples pela sua parte
fracionária. Considerando um prazo fracionário, representado pela fração mista np/q,
teríamos como valor futuro a juros compostos da parte inteira do prazo, FVn,:
FVn = PV .(1 + i )n
E para a parte fracionária do prazo, tomando FVn como valor presente no
segundo cálculo, o valor futuro a juros simples, FVnp/q,:
p
FVn p q = FVn. 1 + i.
q

Porém, como:
FVn = PV .(1 + i )n ,

p
FVn p q = FV .(1 + i) n . 1 + i.
q

5.7 Equivalência de Fluxos de Caixa

Como vimos no item sobre Desconto (2.3.2), as operações de Desconto e
Capitalização são operações inversas. Isso significa que, capitalizando um
determinado valor presente (PV) por um certo número de períodos (n) a uma
determinada taxa (i), obtendo, assim, um valor futuro (FV), se descontarmos esse
valor futuro (FV) à mesma taxa (i), pelo mesmo número de períodos (n), iremos
obter o mesmo valor presente (PV). Esse raciocínio ilustra bem o princípio
fundamental da matemática financeira: o Princípio da Equivalência.
Este princípio nos diz que capitais iguais, situados em épocas diferentes,
têm valores diferentes, mesmo no pressuposto de uma economia com moeda
constante, ou seja, mesmo com inflação nula. Assim, podemos imaginar um capital
situado em uma data futura que, embora diferente, tenha o mesmo valor que outro
capital situado no presente; da mesma forma podemos imaginar um capital no
presente que, embora diferente, possua o mesmo valor que outro colocado no
futuro. Esses capitais diferentes, colocados em datas diferentes, teriam, na mesma
data, o mesmo valor, seriam equivalentes. O mecanismo que estabelece o grau de


24

equivalência e, portanto, que capital situado em uma determinada data é
equivalente a outro em outra data é a taxa de juros.
Isso é de extrema valia quando se trata de comparar valores (fluxos de
caixa) situados em épocas diferentes, pois podemos, indiferentemente, capitalizar
um ou mais fluxos para uma data futura, ou descontar um ou mais fluxos para uma
data presente. Como só podemos comparar, operar algebricamente ou trocar fluxos
de caixa situados na mesma data, utilizamos os recursos da capitalização e do
desconto para "movimentá-los" ao longo do tempo, "atualizando-os" para a mesma
data e, então, realizando a operação que desejamos.
A equivalência permite, na prática, a troca de um título de crédito
(duplicata, nota promissória, etc.) ou de um grupo de títulos situados em uma, ou
diversas datas, por outro título ou por outro grupo situados em outra ou em outras
datas diferentes. Para isso, é necessário que, em uma data qualquer, os seus
valores equivalentes (presentes ou futuros) sejam iguais. Tomando o seguinte
conjunto de fluxos de caixa equivalentes:

PV4
FV3
FV2

0 1 2 3 4 5 6 7 8 9 10

1000

FV4
PV5

Temos que:
PV4 + FV3 + FV2 = 1000 + FV4 + PV5
EXERCÍCIOS

1) Calcular a taxa efetiva anual correspondente a 180% ao ano, capitalizados mensalmente.
2) Qual o tempo necessário para que R$ 2.500,00 produzam o montante de R$ 5.190,40, à taxa de
24% a.a. com capitalizações trimestrais?
3) No fim de quanto tempo os capitais de R$ 5.000,00, a 20% a.a. capitalizados trimestralmente e de
R$ 15.000,00 u.m., a 10% a.a. capitalizados semestralmente produzirão juros iguais?


25

4) No fim de quanto tempo o capital de R$ 500,00 a 10% a.a. e R$ 400,00 a 12% a.a. produzirão
montantes iguais?
5) Qual deve ser a taxa média mensal de inflação para que os preços dupliquem em 3 anos?
6) Qual a taxa anual de juros capitalizada mensalmente que faz com que R$ 2.500,00 produzam o
montante de R$ 5.190,40 em 7 meses e meio?
7) O desconto de um título, pagável em 3 meses e 18 dias, é de R$ 2.164,74. Calcular o Valor
Nominal do título, sabendo que a taxa empregada foi de 30% a.a. com capitalizações mensais.
8) Ao fim de quanto tempo o capital de R$ 5.000,00, a 40% a.a. capitalizados mensalmente
produzirá R$4.500,00 de juros?
9) Duas notas promissórias, de R$ 5.000,00 para 1 ano e 6 meses e de R$ 8.000,00 para 2 anos e 3
meses, serão substituídas por uma única para 3 anos. Estipulando a taxa de 18% a.a. capitalizados
mensalmente para essa operação, calcular o Valor Nominal do título.
10) Uma empresa toma um empréstimo de R$ 200,00 por três anos a 20% a.a. capitalizados
mensalmente. Algum tempo após, propõe saldar a dívida com três pagamentos anuais realizáveis no
fim do 2º, 3º e 4º anos. O primeiro pagamento será de R$ 50,00 e o segundo, de R$ 100,00. Calcular
o valor do último pagamento, sabendo que a taxa do desconto real é de 12% a.a. com capitalizações
mensais.

RESPOSTAS:

1) 435,03% a.a.; 2) 3a1me19d; 3) 7a1me8d; 4) 12a4me19d; 5) 1,94% a.me.; 6) 122,76% a.a. cap.
mens.; 7) R$ 25.450,49; 8) 1a7m18d; 9) R$ 15.683,82; 10) R$ 251,54


26

6. Séries Uniformes

6.1 Classificação, elementos e cálculos

As séries uniformes são constituídas, tanto nas operações de recuperação
de capital (amortização), como nas de formação de capital (capitalização). Nas
operações de amortização (empréstimos, financiamentos, etc.) o valor a ser
amortizado é anterior à série, é a sua causa, e recebe o nome de Valor Atual ou
Valor Presente (PV) de uma série. Nas operações de capitalização, o capital
formado é posterior à série, é a sua conseqüência, e recebe o nome de Montante ou
Valor Futuro (FV) da série. Os fluxos de caixa que constituem a série são
denominados Termos ou Pagamentos (PMT), o número de termos (n) e a taxa no
período (i) são os demais elementos de uma operação com séries uniformes.
As séries uniformes classificam-se em Antecipadas, Imediatas
(Postecipadas) e Diferidas em função da época em que ocorrem os seus fluxos.

6.2 Séries Antecipadas

Em uma Série Antecipada, os fluxos ocorrem no início dos respectivos
períodos. As séries antecipadas são mais freqüentes nas operações de
capitalização, embora sejam utilizadas, também, em operações de amortização.
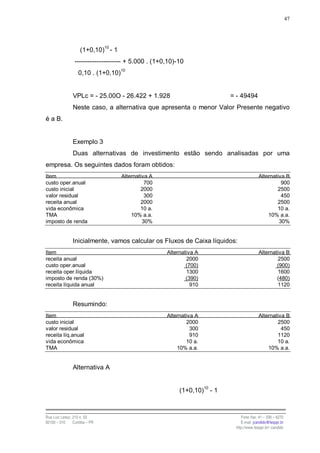
O DFC de uma Série Antecipada tem o seguinte aspecto:

0 1 2 3 4 5 ... n-2 n-1 n

O Valor Presente da uma série Antecipada corresponde à soma dos
valores presentes de todos os termos (PMT) iguais que a compõem. Calculando os
valores presentes de todos os termos e somando-os temos:

PV (a) = PMT .(1 + i )− n+1 + ... + PMT .(1 + i) −3 + PMT .(1 + i )−2 + PMT .(1 + i )−1 + PMT

PV (a) = PMT .[(1 + i)− n+1 + ... + (1 + i )−3 + (1 + i) −2 + (1 + i )−1 + 1]


27

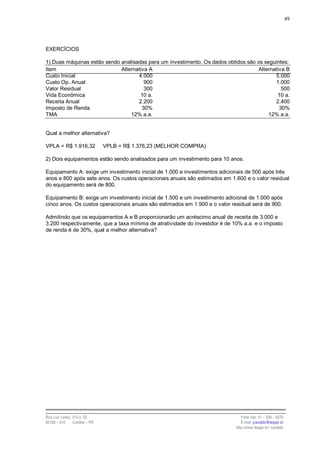
Fazendo:

(1 + i ) = u ,

temos:

PV (a) = PMT .(u − n+1 + ... + u −3 + u −2 + u −1 + 1)

Com a expressão entre parênteses representando a soma dos termos de
uma Progressão Geométrica de razão q = u. A fórmula que permite calcular a soma
dos termos de uma P.G. é:
an .q − a1
Sn = ;
q −1

Substituindo os elementos, temos:

1.u − u − n+1 u − u − n+1
Sn = = ;
u −1 i

Multiplicando ambos os termos da fração por un-1:

u − u − n+1 u n−1 u.u n −1 − u − n+1.u n −1 u n − 1
Sn = . n−1 = = n−1
i u i.u n −1 i.u

un −1 (1 + i )n − 1
PV (a) = PMT . ou PV (a) = PMT .
i.u n−1 i.(1 + i )n −1

O mesmo raciocínio pode ser utilizado para o desenvolvimento das
fórmulas para cálculo do Valor Futuro:

FV (a) = PMT .(1 + i )n + ... + PMT .(1 + i)3 + PMT .(1 + i )2 + PMT .(1 + i )1

FV (a) = PMT .[(1 + i) n + ... + (1 + i )3 + (1 + i )2 + (1 + i )1 ]

Fazendo:

(1 + i ) = u ,

temos:


28

FV (a) = PMT .(u n + ... + u 3 + u 2 + u1 )

Com a expressão entre parênteses representando a soma dos termos de
uma Progressão Geométrica Decrescente de razão q = u-1. Substituindo os
elementos na fórmula do cálculo da soma dos termos da P.G. decrescente:
a1 − an .q
Sn =
1− q

u n − u.u −1 u n − 1
Sn = = ;
1 − u −1 1 − u −1

Multiplicando ambos os termos da fração por u:

u n − 1 u u n .u − 1.u u.(u n − 1) un −1
Sn = . = = = u.
1 − u −1 u 1.u − u −1.u u −1 i

u n −1 (1 + i) n − 1
FV (a) = PMT .u. ou FV (a) = PMT .(1 + i ).
i i

6.3 Séries Imediatas

Em uma série Imediata, os fluxos ocorrem no final dos respectivos
períodos.
As séries Imediatas são mais características das operações de
amortização, embora possam ser utilizadas, também, em operações especiais de
capitalização na constituição de fundos de reembolso para o resgate de dívidas ou
fundos de provisão para a substituição de equipamentos.
O DFC de uma série Imediata tem o seguinte aspecto:
0 1 2 3 4 5 6 ... n-1 n

O Valor Presente da uma série Imediata pode ser obtido pela seguinte
fórmula:
un −1 (1 + i )n − 1
PV (i ) = PMT . ou PV (i) = PMT .
i.u n i.(1 + i )n


29

(Ver Tabela 3 - P.65)

O Valor Futuro é calculado por:

un −1 (1 + i )n − 1
FV (i ) = PMT . ou FV (i) = PMT .
i i


6.4 Séries Diferidas

Em uma série Diferida, os fluxos ocorrem no final dos respectivos
períodos, posteriores a um prazo de carência ou diferimento.
As séries Diferidas são praticamente exclusivas das operações de
amortização, embora sejam utilizadas, ainda que raramente, em operações de
capitalização nos mesmos casos previstos nas séries imediatas. As séries diferidas
incluem no cálculo um elemento adicional: a carência ou prazo de diferimento (m).
O DFC de uma série Diferida tem o seguinte aspecto:
0 1 2 3 4 ... n-1 n

0 1 2 ... m m+1 m+2 m+3 m+4 ... m+n-1 m+ n

O Valor Presente da uma série Diferida pode ser obtido pela seguinte
fórmula:

un −1 (1 + i) n − 1
PV (d ) = PMT . ou PV (d ) = PMT .
i.u m + n i.(1 + i)m + n

O Valor Futuro é calculado de forma idêntica ao das séries imediatas, já
que o prazo de carência ou diferimento não interfere nesse cálculo:

un −1 (1 + i) n − 1
FV (d ) = PMT . ou FV (d ) = PMT .
i i
Todos esses valores podem ser calculados pelas fórmulas acima, pelo
emprego de tábuas financeiras e com as calculadoras financeiras, e, ainda, por
decomposição dos fluxos de caixa.


30

6.5 Séries Gradientes

Séries Gradientes ou Séries em Gradiente são séries de pagamentos
cujos termos crescem em progressão aritmética de razão G, sendo que o primeiro
termo também é igual a G e ocorre no segundo período.
O DFC de uma Série Gradiente tem o seguinte aspecto:

0 1 2 3 4 5 6 ... n-1 n

G 2G 3G 4G 5G n-2G n-1G

Para efeito de cálculo, a Série Gradiente é convertida em uma série
imediata equivalente, segundo o fator de conversão:

1 n i
− . n
i i u −1

Assim, o valor do termo (PMT) de uma Série Imediata equivalente a uma
Série Gradiente em G é:

1 n i
P M T (i ) = G . − . n
i i u −1


31

EXERCÍCIOS

Calcule o valor equivalente das seguintes séries, usando a taxa de 10%:
1)

2)

3)

RESPOSTAS:

1) PV=R$ 1.071,16; 2) FV=R$ 14.024,93; 3) PV=R$ 2.677,23


32

6.6 Decomposição de Fluxos de Caixa

Nem todas as operações financeiras se comportam de forma uniforme. As
operações mais complexas parecem conjuntos desordenados de fluxos de caixa
quando traduzidas para um diagrama. No entanto, podemos decompô-las em dois
ou mais conjuntos de pagamentos isolados e séries uniformes, simplificando o seu
cálculo. A decomposição de fluxos de caixa é feita por "cortes" verticais ou
horizontais nos diagramas, que, assim, são decompostos em outros diagramas mais
simples e uniformes, como no exemplo a seguir:

Que pode ser decomposto horizontalmente em:


33

7. Sistemas de financiamento

São vários os sistemas utilizados para o pagamento de um empréstimo ou
de um financiamento. Trataremos dos mais freqüentes no nosso mercado. Para
exemplificarmos, utilizaremos como exemplo, o empréstimo do capital de R$
30.000,00, a 10% ao mês, por cinco meses.


34

7.1 Sistema do Montante

É o sistema no qual o devedor restitui ao credor, ao final de um prazo
estipulado, o capital e os juros correspondentes. O cálculo é feito pela fórmula do
Valor Futuro de um pagamento único:
FV = PV . (1 + i)n

FV = 30000 . (1 + 0,10)5 = R$ 48.315,30

7.2 Sistema do Juro Antecipado (Descontos)

É o sistema utilizado no cálculo dos penhores e nas operações de
empréstimo com desconto de duplicatas. É, também, a forma utilizada para cálculo
de taxas e comissões cobradas antecipadamente (flat), como os seguros de crédito,
o IOF, etc. Em geral, o desconto é calculado no regime de capitalização simples.
Porém, como os juros são pagos antecipadamente, a taxa de juros efetiva da
operação é bastante diferente da taxa de desconto anunciada, o que
freqüentemente conduz a erros de avaliação. Vejamos como ficaria a operação com
a taxa de 10% ao mês para o desconto simples:

PV
FV = ----------
1 - i.n

30000
FV = --------------- = R$ 60.000,00
1 - 0,10 . 5

Assim, para um empréstimo de R$ 30.000,00, temos um Valor Futuro de
R$ 60.000,00 em 5 meses. Substituindo esses valores na fórmula do Valor Futuro
de um pagamento único a juros compostos, temos:

FV = PV . (1 + i)n


35

60000 = 30000 . (1 + i)5

60000
--------- = (1 + i)5
30000

2 = (1 + i)5

1 + i = 21/5

1 + i = 1,1487

i = 0,1487 => 14,87% a.m.

Sendo 14,87% ao mês, portanto, a taxa efetiva de juros. Essa diferença se
acentua à medida que cresce o prazo e a taxa de desconto.

7.3 Sistema Francês ou Sistema Price

É o sistema em que o pagamento do empréstimo ou financiamento é feito
através de prestações iguais, a intervalos de tempo constantes, geralmente ao mês.
Essas prestações são compostas de duas partes: os juros mensais calculados sobre
o saldo devedor e o restante que compõe uma quota destinada a amortizar o
principal da dívida.
O cálculo das prestações é feito pelas fórmulas das séries uniformes.
Utilizando o exemplo para uma série uniforme imediata, temos:

(1+i)n - 1
PV(i) = PMT . -------------
i . (1+i)n


36

(1+0,10)5 - 1
30000 = PMT . --------------------
0,10 . (1+0,10)5

0,6105
30000 = PMT . ----------
0,1611

30000 = PMT . 3,7908

30000
PMT = --------- = R$ 7.913,92
3,7908

Através do seguinte Plano de Amortização, podemos observar a evolução
dos principais componentes da operação, período a período.

Plano de Amortização - Sistema Francês
Capital : 30.000,00
Nº de Pagamentos : 5
Taxa de Juros : 10,00%

Per. Pagamento Juros Quota de Fundo de Saldo De-
(n) (PMT) Amortização Amortização vedor (PV)

0 - - - - 30000,00
1 7913,92 3000,00 4913,92 4913,92 25086,07
2 7913,92 2508,60 5405,31 10319,24 19680,75
3 7913,92 1968,07 5945,84 16265,08 13734,91
4 7913,92 1373,49 6540,43 22805,52 7194,47
5 7913,92 719,44 7194,47 30000,00 0,00

7.4 Sistema de Amortizações Constantes

É o sistema pelo qual o empréstimo ou financiamento é pago através de
prestações decrescentes. A quota destinada à amortização do principal é fixa e
corresponde à divisão do principal pelo número de prestações. A essa quota são


37

acrescentados os juros calculados sobre o saldo devedor do período anterior, para
formar a prestação do período.
O Plano de Amortização a seguir ilustra bem a solução do nosso exemplo
por esse sistema:
Plano de Amortização - Sistema de Amortizações Constantes
Capital : 30000,00
Nº de Pagamentos : 5
Taxa de Juros : 10,00%

Per. Pagamento Juros Quota de Fundo de Saldo De-
(n) (PMT) Amortização Amortização vedor (PV)

0 - - - - 30000,00
1 9000,00 3000,00 6000,00 6000,00 24000,00
2 8400,00 2400,00 6000,00 12000,00 18000,00
3 7800,00 1800,00 6000,00 18000,00 12000,00
4 7200,00 1200,00 6000,00 24000,00 6000,00
5 6600,00 600,00 6000,00 30000,00 0,00


38

EXERCÍCIOS
1) Uma família decidiu comprar um refrigerador a crédito. O esquema de pagamento oferecido pela
loja é o seguinte:
15.03.02 R$ 500,00
15.06.02 R$ 300,00
15.07.02 R$ 300,00
15.08.02 R$ 300,00
15.09.02 R$ 300,00
Sabendo que a taxa de juros é de 5% ao mês, determine o valor do refrigerador em 15.05.02.
2) Qual o valor presente de uma série de oito prestações mensais imediatas de R$ 5.000,00,
sabendo-se que a taxa mensal de juros é de 3,0%?
3) Qual o valor da prestação mensal de um fundo de investimentos que capitaliza os depósitos à
taxa composta de 10% ao ano capitalizados mensalmente, para se obter, no fim de 20 anos, o
montante de R$ 500.000,00?
4) Em quanto tempo duplicará um capital aplicado a uma taxa de juros de 1,25% ao mês?
5) Logo que tenha economizado R$ 10.000,00 em valores de hoje, o Sr. Saddam Sahva pretende
instalar uma quitanda. Se economizar R$ 500,00 por mês, investindo-os a 1,0% ao mês, quantos
meses serão necessários para que o Sr. Saddam obtenha a importância desejada, sabendo-se que a
inflação mensal é de 0,485%?
6) O Sr. Komero Toda Furuta comprou uma Kombi em 10 prestações mensais iguais. Sabendo que a
Kombi tem seu preço à vista fixado em R$ 30.000,00 e que a taxa de financiamento é de 1,75% ao
mês, determine:
a) O valor da prestação.
b) O saldo devedor após o pagamento da 5ª parcela.

RESPOSTAS:

1) R$ 1.615,04 2) R$ 35.098,46 3) R$ 658,44 4) 4 anos, 7 meses e 24 dias 5) 20 meses 6) R$
3.296,26 e R$15.650,17


39

8. Análise de alternativas de financiamento e investimento

A Análise de Alternativas de Financiamento e Investimento conta com um
conjunto de técnicas da Engenharia Econômica que permitem a comparação, de
forma científica, entre alternativas diferentes. Ao permitir que essas diferenças
sejam explicitadas de forma quantitativa, elas constituem ferramenta da maior
utilidade no processo de tomada de decisões em qualquer empresa, de qualquer
porte ou ramo de atividade.
São exemplos típicos da utilização dessas técnicas as alternativas de
investimento financeiro, de distribuição em marketing, de automatização na
contabilidade, de planos de carreira em administração de pessoal, de aquisição e
substituição de equipamentos na administração da produção, na engenharia de
produto, etc.
Para ser eficiente, a Análise de Investimentos pressupõe alguns princípios
fundamentais:
− Não existe decisão com alternativa única, todas as alternativas devem ser
consideradas;
− Somente são comparáveis alternativas homogêneas, não se pode optar
entre pouco retorno com pouco investimento e muito retorno com muito
investimento, por exemplo;
− Apenas as diferenças entre as alternativas são relevantes, não perca tempo
com o que é comum a elas;
− Os critérios para decisão entre alternativas econômicas devem levar em
consideração o valor do dinheiro no tempo, o princípio da equivalência é
básico;
− Não devem ser subestimados os problemas relativos ao racionamento de
capital, a menos que isso não seja problema para você;
− Decisões separáveis são tomadas separadamente;
− As previsões são necessariamente falhas e o seu grau e tipos de incerteza
devem ser explicitados;
− O evento qualitativo não quantificava monetariamente devem ser claramente
especificados;
− A retroalimentação (feedback) de informações é fundamental e é a única
maneira de minimizar o impacto dos erros das previsões;
− Os dados relevantes são os econômicos e gerenciais, os dados contábeis só
são importantes na avaliação após o Imposto de Renda. Não importa de um
equipamento é depreciado contabilmente em 10 anos, se está obsoleto em 5
anos.

E tem, também, algumas limitações:


40

− A escolha do método, que deve considerar o aspecto mais abrangente do
problema, uma vez que é impossível levar em consideração e quantificar
todas as variáveis em situações reais. Premissas, restrições e limitações
devem ser claramente caracterizadas;
− Os modelos estudados pressupõem taxas de juros e retorno iguais, embora
no mercado as taxas de juros (empréstimos) sejam sempre maiores que as
taxas de retorno (aplicação). A taxa de retorno será denominada doravante
de Taxa Mínima de Atratividade, ou simplesmente TMA, refletindo a menor
taxa de retorno aceitável para um investimento;
− Os modelos pressupõem taxas constantes, o que recomenda a utilização de
uma média das taxas projetadas, ou a explicitação de que a solução está
vinculada às circunstâncias presentes;
− Os modelos pressupõem viabilidade econômica e financeira para o fluxo de
caixa real final;
− Os modelos levam em consideração que os fluxos de caixa ocorrem no final
dos respectivos períodos (anos), embora a maioria possa ocorrer durante o
período. Nesses casos, esses fluxos de caixa são os valores equivalentes,
no final do período, dos demais fluxos ocorridos durante aquele período.
− A complexidade do modelo deve ser compatível com a confiabilidade dos
dados assumidos.

8.1 Métodos de Análise

As principais técnicas utilizadas pela Análise de Investimentos são os
métodos de análise, também chamados “Métodos Equivalentes Para Avaliação de
Alternativas de Financiamento e Investimento”. Em seguida, veremos uma
apresentação desses métodos e suas principais características.

8.1.1 Método do Custo Anual

Consiste em transformar os fluxos de caixa das alternativas em séries
uniformes equivalentes, utilizando uma taxa de juros igual à Taxa Mínima de
Atratividade. É possível, então, chegar a um Custo Anual Equivalente, que servirá
de parâmetro para comparação entre as alternativas.
Cabe ressaltar que, embora chamado de Método do Custo Anual, o
método se presta a análises em períodos diferentes do ano. É importante, no
entanto que, por ora, as alternativas tenham a mesma duração de tempo, i.e., a
mesma Vida Econômica.
Vejamos o Exemplo 1, a seguir:


41

Alterna- Investimento Despesas Valor
tiva Inicial Anuais Residual

A - 10000,00 -
B 15000,00 5000,00 -
C 20000,00 4000,00 2000,00
TMA: 10% ao ano
Vida Econômica: 10 anos

Solução:
. Alternativa A
Custo Anual Dado = 10000

. Alternativa B
Custo Anual Equivalente do investimento inicial (PV):

0,10 . 1,1010
PMT(PV) = 15.000 . ----------------- = 2441
1,1010 - 1
-----
Custo Anual Total = 7441


42

. Alternativa C


0,10 . 1,1010
PMT(PV) = 20000 . --------------- = 3255
1,1010 - 1

Retorno Anual Equivalente do Valor Residual (FV):

0,10
PMT(FV) = -2000 . ------------ = - 125
1,1010 - 1
-----

A alternativa C é a mais vantajosa por apresentar os menores custos
anuais equivalentes.

Exemplo 2

Uma companhia deseja mecanizar uma operação de movimentação de
materiais em seu almoxarifado. Atualmente, esta operação é realizada manualmente
por uma equipe de operários. Os custos anuais com salários e encargos sociais são
de R$ 8000,00.
A mecanização será obtida com a aquisição de um equipamento cujo valor
é de R$ 20000,00. Espera-se uma redução nos custos com mão-de-obra a R$
2000,00 ao ano. As despesas anuais de operação são estimadas em R$ 500,00 de
energia, R$ 1.500,00 de manutenção e R$ 500,00 de seguro e demais despesas.


43

O equipamento tem vida econômica de 10 anos e um valor de revenda de
R$ 2000,00. A uma TMA de 18% a.a., qual a alternativa mais vantajosa
economicamente?
Solução:

. Alternativa A

. Alternativa B

0,18 . 1,1810
PMT(PV) = 20000 . --------------- = 4450
1,1810 - 1
Despesas Anuais = 4500
- Mão-de-Obra = 2000
- Energia = 500
- Manutenção = 1500
- Seguro, etc. = 500

Retorno Anual Equivalente do Valor de Revenda (FV):
0,18
PMT(FV) = -2000 . ------------ = - 85
1,1810 - 1
------

O maior custo anual da segunda alternativa a desaconselha como decisão
econômica.


44

EXERCÍCIOS

1) Calcular e comparar os custos anuais dos motores A e B, cuja compra é considerada para 12 anos
de serviço a uma TMA de 10%a.a.

Item Motor A Motor B
Custo Inicial 2.500 4.000
Valor Residual Estimado - 1.000
Custo Anual de Energia 500 300
Custo Anual de Reparos 300 220

CAA = R$ 1.166,91 CAB = 1.060,29 (MELHOR COMPRA)

2) Um serviço de encanamento precisa ser executado em uma empresa. As alternativas que se
apresentam são as seguintes:
Item Tubo 30 cm Tubo 50 cm
Custo Anual de Operação 6.700 3.850

O período de serviço esperado é de sete anos, após os quais o encanamento será removido com
Valor Residual previsto de 5% de seu custo. O retorno mínimo exigido é de 8% ao ano. Comparar os
custos anuais.

CAA = 10.615,84 CAB = 9.817,00 (MELHOR COMPRA)


45

8.1.2 Método do Valor Presente Líquido

Consiste em se calcular a soma algébrica dos valores equivalentes de
todos os fluxos de caixa no período zero utilizando a Taxa Mínima de Atratividade. A
soma desses Valores Presentes resulta no Valor Presente Líquido da alternativa. A
alternativa mais indicada é aquela que apresenta o maior retorno em relação a um
investimento, ou o menor custo. É fundamental que se observe o sinal dos
respectivos fluxos de caixa.
Assim, um VPL positivo significa que o Valor Presente dos retornos é
maior que o Valor Presente dos investimentos e das despesas. Quanto maior o VPL
positivo, maior essa diferença e, portanto, maior a razão entre retorno e
investimento. Se VPL=0 (nulo) o projeto oferece a mesma rentabilidade que a
alternativa de investimento financeiro remunerada pela TMA. Se VPL<0 (negativo),
o Valor Presente dos desembolsos supera o Valor Presente dos recebimentos, o
que não recomenda economicamente o projeto. No caso da escolha obrigatória
entre alternativas com VPL<0, a opção mais econômica será a que apresentar o
menor VPL negativo. Tomemos o Exemplo 1 do método anterior:

. Alternativa A
(1+0,10)10 - 1
VPLA = - PV(PMT) = - 10000 . -------------------- = - 61.446
0,10 . (1+0,10)10
. Alternativa B
(1+0,10)10 - 1
VPLB = - 15000 - PV(PMT) = - 15000 - 5000 . ----------------
0,10.(1+0,10)10

VPLB = - 15000 - 30723 = - 45723

. Alternativa C


46

VPLc = - 20000 - PV(PMT) + PV(FV) = - 20000 - 4000 .

(1+0,10)10 - 1
. --------------------- + 2000 . (1+0,10)-10
0,10 . (1+0,10)10

VPLc = - 2000O - 24578 + 771 = - 43807
A melhor alternativa é C, pois apresenta o menor VPL negativo, o que
significa menor custo real.

Exemplo 2
Escolher entre os seguintes planos, com vida econômica de 10 anos,
usando uma TMA de 10% ao ano:
Item Plano A Plano B Plano C
Despesas Anuais 8000 5100 4300
Custo Inicial - 15000 25000
Valor Residual - - 5000
Solução:
. Plano A
(1+0,10)10 - 1
VPLA = - PV(PMT) = - 8000 . --------------------- = - 49157
0,10 . (1+0,10)10
. Plano B
(1+0,10)10 - 1
VPLB = - 15.000 - PV(PMT) = - 15.000 - 5.100 . ----------------
0,10.(1+0,10)10

VPLB = - 15.000 - 31.337 = = - 46337

. Plano C

VPLc = - 25.000 - PV(PMT) + PV(FV) = - 25.000 - 4.300 .


47

(1+0,10)10 - 1
--------------------- + 5.000 . (1+0,10)-10
0,10 . (1+0,10)10

VPLc = - 25.00O - 26.422 + 1.928 = - 49494
Neste caso, a alternativa que apresenta o menor Valor Presente negativo
é a B.

Exemplo 3
Duas alternativas de investimento estão sendo analisadas por uma
empresa. Os seguintes dados foram obtidos:
Item Alternativa A Alternativa B
custo oper.anual 700 900
custo inicial 2000 2500
valor residual 300 450
receita anual 2000 2500
vida econômica 10 a. 10 a.
TMA 10% a.a. 10% a.a.
imposto de renda 30% 30%

Inicialmente, vamos calcular os Fluxos de Caixa líquidos:
receita anual 2000 2500
custo oper.anual (700) (900)
receita oper.líquida 1300 1600
imposto de renda (30%) (390) (480)
receita líquida anual 910 1120

Resumindo:
custo inicial 2000 2500
valor residual 300 450
receita líq.anual 910 1120
vida econômica 10 a. 10 a.
TMA 10% a.a. 10% a.a.

Alternativa A

(1+0,10)10 - 1


48

VPLA= -2000 + PV(PMT) + PV(FV)= -2000 + 910 . ------------------- +
0,10.(1+0,10)10

+ 300 . (1+0,10)-10 = - 2000 + 5592 + 116 = 3708

. Alternativa B

(1+0,10)10 - 1
VPLB= -2500 + PV(PMT) + PV(FV)= -2000 + 1120 .------------------ +
0,10.(1+0,10)10

+ 450 . (1+0,10)-10 = - 2500 + 6882 + 173 = 4555

A alternativa B é a melhor uma vez que apresenta o maior Valor Presente
Líquido positivo.


49

EXERCÍCIOS

1) Duas máquinas estão sendo analisadas para um investimento. Os dados obtidos são os seguintes:
Custo Op. Anual 900 1.000
Valor Residual 300 500
Vida Econômica 10 a. 10 a.
Receita Anual 2.200 2.400
Imposto de Renda 30% 30%
TMA 12% a.a. 12% a.a.

Qual a melhor alternativa?

VPLA = R$ 1.916,32 VPLB = R$ 1.376,23 (MELHOR COMPRA)

2) Dois equipamentos estão sendo analisados para um investimento para 10 anos.

Equipamento A: exige um investimento inicial de 1.000 e investimentos adicionais de 500 após três
anos e 800 após sete anos. Os custos operacionais anuais são estimados em 1.600 e o valor residual
do equipamento será de 800.

Equipamento B: exige um investimento inicial de 1.500 e um investimento adicional de 1.000 após
cinco anos. Os custos operacionais anuais são estimados em 1.900 e o valor residual será de 900.

Admitindo que os equipamentos A e B proporcionarão um acréscimo anual de receita de 3.000 e
3.200 respectivamente, que a taxa mínima de atratividade do investidor é de 10% a.a. e o imposto
de renda é de 30%, qual a melhor alternativa?


50

8.1.3 Método da Taxa Interna de Retorno

Consiste em se determinar a taxa para a qual o Valor Presente Líquido é
igual a zero, ou seja, a taxa para a qual o Valor Presente dos retornos do projeto é
igual ao Valor Presente dos investimentos necessários.
Uma comparação entre a Taxa Interna de Retorno (TIR) e a Taxa Mínima
de Atratividade (TMA) nos permite avaliar a alternativa. Se TIR > TMA, o
investimento propicia um retorno superior ao de uma aplicação financeira com a
rentabilidade da TMA. Se TIR = TMA, a rentabilidade é igual à da aplicação
financeira e, finalmente, se TIR < TMA, o investimento não é economicamente
recomendável, uma vez que propicia um retorno inferior ao de uma aplicação
financeira com rentabilidade da TMA. Uma análise entre diversas alternativas
economicamente viáveis conduz à escolha da alternativa com a maior Taxa Interna
de Retorno.
Assim, o método nos permite uma análise de sensibilidade do
investimento, ou seja, nos permite saber qual a Taxa Mínima de Atratividade que
viabiliza determinado investimento. Reduzida a TMA a um patamar inferior a TIR de
um determinado investimento, antes economicamente inviável, este passa a se
viabilizar por redução da TMA.
Para utilização desse método, é necessário que as alternativas tenham o
mesmo investimento e que possam ser representadas por um Diagrama de Fluxos
de Caixa Ordinário, isto é, que sejam constituídas de um único investimento feito no
período zero, seguido de uma série de retornos líquidos.
No caso dos investimentos serem diferentes, pode-se decompô-los de
forma a trabalhar com um conjunto de investimentos iguais. Já no caso de se ter
investimentos múltiplos, o método não deve ser aplicado, uma vez que serão
obtidas taxas de retorno múltiplas, uma para cada inversão de fluxo de caixa entre
investimentos e retornos.
Tomemos o exemplo representado pelo fluxo de caixa abaixo, durante sete
anos:


51

Ano Receita Desembolso Fluxo Líquido
0 0 (10900) (10900)
1 1800 (800) 1000
2 1800 (550) 1250
3 1800 (570) 1230
4 1800 (450) 1350
5 1800 (360) 1440
6 1800 (430) 1370
7 23700 (1510) 22190

Solução:
Calculando o VPL para uma taxa arbitrária de 15% a.a., teremos:
VPL = 2146
Como o Valor Presente Líquido resultou positivo, precisamos arbitrar outra
taxa que minimize o Valor Presente dos fluxos positivos, portanto uma taxa maior,
por exemplo, 20% a.a.:
VPL = (605)
O Valor Presente Líquido negativo representa uma inversão de sinal em
relação à taxa anterior, o que significa que a Taxa Interna de Retorno (que faz VPL
= 0) está entre 15% a.a. e 20% a.a.. Através de uma simplificação do processo,
estimamos a TIR por Interpolação Linear das taxas utilizadas:
2146 --> 15% 0 - 2146 i - 15%
0 --> i --------------- = ------------- => i ~ 18,9% a.a.
- 605 --> 20% - 605 - 2146 20% - 15%
Obviamente, esta forma de cálculo, trabalhosa e imperfeita devido à
utilização da interpolação linear, pode ser substituída, com vantagens, pela
utilização das funções financeiras avançadas encontradas nas calculadoras
financeiras mais completas.
É importante observar que o conceito de Taxa Interna de Retorno está
intimamente vinculado à Vida Econômica do investimento. Assim, o investimento
acima possibilita uma TIR de aproximadamente 18,9% ao ano para uma Vida
Econômica de sete anos. Isso quer dizer que o capital investido será remunerado a,
aproximadamente 18,9% ao ano e que o investimento será totalmente recuperado
em sete anos.


52

EXERCÍCIOS

1) A respeito de um projeto são conhecidos os seguintes dados:

Item Valor
Custo Inicial 12.000
Custo Op. Anual 1.506
Valor Residual 2.000
Vida Econômica 25 a.
Receita Anual 2.590
Calcular a Taxa Interna de Retorno do investimento.

2) Uma loja vende amplificadores a R$ 2.500 cada um, mas R$ 500 deverão ser pagos de entrada e
R$ 500 no fim de cada mês nos próximos quatro meses, "sem cobrança de juros". Discutindo a
possível compra, você descobre que pode comprar o amplificador por R$ 2.250 à vista. Você
também fica sabendo que, comprando a prazo, haverá a cobrança, no ato da compra, de R$ 50
referentes a serviços e despesas contratuais. Que taxa de juros será realmente paga se a compra for
feita em prestações?

3) Duas alternativas estão sendo consideradas para um investimento de R$ 4.000 por dez anos. Os
demais dados seguem:

Custo Op.Anual 1.100 1.600
Valor Residual 400 600
Receita Anual 2.000 2.500
Determinar a melhor alternativa.

4) Uma bomba de água essencial para um processo industrial pode ser comprada de dois
fornecedores. O fornecedor A vende a bomba por R$ 100.000 e a despesa mensal de operação e
manutenção é estimada em R$ 12.000. A bomba do fornecedor B custa R$ 170.000 e a despesa
mensal de operação e manutenção é estimada em R$ 8.000. Se ambas as bombas serão usadas por
cinco anos e a taxa mínima de retorno exigida é de 10% ao mês, qual das bombas deve ser
escolhida? Qual seria a resposta do problema se a TMA fosse de 4% a.m.?


53

8.2 Classificação de Alternativas

8.2.1 Alternativas Singulares

Na análise de alternativas singulares pode-se utilizar os métodos do Valor
Presente Líquido e da Taxa Interna de Retorno, como fizemos para cada alternativa
nos exemplos desses dois métodos. A análise, nesse caso, é simples. O
investimento que possua Valor Presente Líquido positivo (VPL > 0) é
economicamente viável, pois possibilita um retorno sobre o investimento superior ao
propiciado por uma aplicação financeira à taxa Mínima de Atratividade. No caso do
método da Taxa Interna de Retorno, a conclusão é a mesma para um investimento
que possua a Taxa Interna de Retorno maior que a Taxa Mínima de Atratividade.

8.2.2 Alternativas Múltiplas

Na análise de alternativas múltiplas os métodos do Custo Anual e do Valor
Presente Líquido aplicam-se como fizemos nos respectivos exemplos. Já o método
da Taxa Interna de Retorno, por pressupor investimentos iguais, exige, no caso de
investimentos diferentes, a decomposição em fluxos complementares, de modo a
ser definido o fluxo de caixa incremental de um projeto em relação a outro. Este
seria o fluxo de caixa composto apenas pelas diferenças incrementais de um projeto
em relação a outro. Para um conjunto de alternativas com investimentos diferentes,
procederíamos da seguinte maneira:
Ordenar as alternativas em ordem crescente de investimentos.
Determinar a TIR da primeira alternativa e compará-la com a TMA. Se a
TIR < TMA, abandonar esta alternativa e repetir a análise para a alternativa
seguinte e, assim, sucessivamente até a obtenção de uma alternativa
economicamente viável.
A partir da primeira alternativa viável, calcula-se a Taxa de Retorno
incremental da próxima alternativa. A Taxa de retorno incremental é a TIR do fluxo
de caixa incremental de um projeto me relação a outro com investimento menor.
Este fluxo de caixa incremental é o fluxo de caixa composto pelas diferenças
algébricas entre os fluxos de caixa da alternativa com investimento maior e a


54

primeira alternativa viável. A Taxa de Retorno incremental é, também, comparada
com a Taxa Mínima de Atratividade. A primeira alternativa é remunerada pela sua
TIR e a segunda alternativa é remunerada, em parte pela TIR, e na parte
incremental, pela Taxa de Retorno incremental. Se a Taxa de Retorno incremental
for maior que a TMA, a alternativa é, também, viável.

8.2.3 Alternativas com Vidas Econômicas Diferentes

No caso de se analisar alternativas com diversas vidas econômicas,
somente os métodos do Custo Anual e do Valor Presente são aplicáveis. O método
do Custo Anual não sofre distorções graves com a diferença de Vidas Econômicas,
o que ocorre com o método do Valor Presente Líquido. Em ambos os casos, a
diferença pode ser contornada levando-se em consideração a possibilidade de
reinvestimento. Define-se assim um prazo que seja o Mínimo Múltiplo Comum entre
os prazos das alternativas propostas e repete-se o fluxo de caixa de cada
alternativa o número de vezes necessário para preencher o prazo comum. Recai-se
então na análise com vidas iguais.


55

ANEXOS


56

VALOR PRESENTE DE UM PAGAMENTO
n 1,0% 2,0% 3,0% 4,0% 5,0% 6,0% 7,0% 8,0% 9,0% 10,0%
1 0,990099 0,980392 0,970874 0,961538 0,952381 0,943396 0,934579 0,925926 0,917431 0,909091
2 0,980296 0,961169 0,942596 0,924556 0,907029 0,889996 0,873439 0,857339 0,841680 0,826446
3 0,970590 0,942322 0,915142 0,888996 0,863838 0,839619 0,816298 0,793832 0,772183 0,751315
4 0,960980 0,923845 0,888487 0,854804 0,822702 0,792094 0,762895 0,735030 0,708425 0,683013
5 0,951466 0,905731 0,862609 0,821927 0,783526 0,747258 0,712986 0,680583 0,649931 0,620921
6 0,942045 0,887971 0,837484 0,790315 0,746215 0,704961 0,666342 0,630170 0,596267 0,564474
7 0,932718 0,870560 0,813092 0,759918 0,710681 0,665057 0,622750 0,583490 0,547034 0,513158
8 0,923483 0,853490 0,789409 0,730690 0,676839 0,627412 0,582009 0,540269 0,501866 0,466507
9 0,914340 0,836755 0,766417 0,702587 0,644609 0,591898 0,543934 0,500249 0,460428 0,424098
10 0,905287 0,820348 0,744094 0,675564 0,613913 0,558395 0,508349 0,463193 0,422411 0,385543
11 0,896324 0,804263 0,722421 0,649581 0,584679 0,526788 0,475093 0,428883 0,387533 0,350494
12 0,887449 0,788493 0,701380 0,624597 0,556837 0,496969 0,444012 0,397114 0,355535 0,318631
13 0,878663 0,773033 0,680951 0,600574 0,530321 0,468839 0,414964 0,367698 0,326179 0,289664
14 0,869963 0,757875 0,661118 0,577475 0,505068 0,442301 0,387817 0,340461 0,299246 0,263331
15 0,861349 0,743015 0,641862 0,555265 0,481017 0,417265 0,362446 0,315242 0,274538 0,239392
16 0,852821 0,728446 0,623167 0,533908 0,458112 0,393646 0,338735 0,291890 0,251870 0,217629
17 0,844377 0,714163 0,605016 0,513373 0,436297 0,371364 0,316574 0,270269 0,231073 0,197845
18 0,836017 0,700159 0,587395 0,493628 0,415521 0,350344 0,295864 0,250249 0,211994 0,179859
19 0,827740 0,686431 0,570286 0,474642 0,395734 0,330513 0,276508 0,231712 0,194490 0,163508
20 0,819544 0,672971 0,553676 0,456387 0,376889 0,311805 0,258419 0,214548 0,178431 0,148644
21 0,811430 0,659776 0,537549 0,438834 0,358942 0,294155 0,241513 0,198656 0,163698 0,135131
22 0,803396 0,646839 0,521893 0,421955 0,341850 0,277505 0,225713 0,183941 0,150182 0,122846
23 0,795442 0,634156 0,506692 0,405726 0,325571 0,261797 0,210947 0,170315 0,137781 0,111678
24 0,787566 0,621721 0,491934 0,390121 0,310068 0,246979 0,197147 0,157699 0,126405 0,101526
25 0,779768 0,609531 0,477606 0,375117 0,295303 0,232999 0,184249 0,146018 0,115968 0,092296
26 0,772048 0,597579 0,463695 0,360689 0,281241 0,219810 0,172195 0,135202 0,106393 0,083905
27 0,764404 0,585862 0,450189 0,346817 0,267848 0,207368 0,160930 0,125187 0,097608 0,076278
28 0,756836 0,574375 0,437077 0,333477 0,255094 0,195630 0,150402 0,115914 0,089548 0,069343
29 0,749342 0,563112 0,424346 0,320651 0,242946 0,184557 0,140563 0,107328 0,082155 0,063039
30 0,741923 0,552071 0,411987 0,308319 0,231377 0,174110 0,131367 0,099377 0,075371 0,057309
31 0,734577 0,541246 0,399987 0,296460 0,220359 0,164255 0,122773 0,092016 0,069148 0,052099
32 0,727304 0,530633 0,388337 0,285058 0,209866 0,154957 0,114741 0,085200 0,063438 0,047362
33 0,720103 0,520229 0,377026 0,274094 0,199873 0,146186 0,107235 0,078889 0,058200 0,043057
34 0,712973 0,510028 0,366045 0,263552 0,190355 0,137912 0,100219 0,073045 0,053395 0,039143
35 0,705914 0,500028 0,355383 0,253415 0,181290 0,130105 0,093663 0,067635 0,048986 0,035584
36 0,698925 0,490223 0,345032 0,243669 0,172657 0,122741 0,087535 0,062625 0,044941 0,032349
42 0,658419 0,435304 0,288959 0,192575 0,128840 0,086527 0,058329 0,039464 0,026797 0,018260
48 0,620260 0,386538 0,241999 0,152195 0,096142 0,060998 0,038867 0,024869 0,015978 0,010307
54 0,584313 0,343234 0,202670 0,120282 0,071743 0,043001 0,025899 0,015672 0,009527 0,005818
60 0,550450 0,304782 0,169733 0,095060 0,053536 0,030314 0,017257 0,009876 0,005681 0,003284


57

VALOR FUTURO DE UM PAGAMENTO
n 1,0% 2,0% 3,0% 4,0% 5,0% 6,0% 7,0% 8,0% 9,0% 10,0%
1 1,010000 1,020000 1,030000 1,040000 1,050000 1,060000 1,070000 1,080000 1,090000 1,100000
2 1,020100 1,040400 1,060900 1,081600 1,102500 1,123600 1,144900 1,166400 1,188100 1,210000
3 1,030301 1,061208 1,092727 1,124864 1,157625 1,191016 1,225043 1,259712 1,295029 1,331000
4 1,040604 1,082432 1,125509 1,169859 1,215506 1,262477 1,310796 1,360489 1,411582 1,464100
5 1,051010 1,104081 1,159274 1,216653 1,276282 1,338226 1,402552 1,469328 1,538624 1,610510
6 1,061520 1,126162 1,194052 1,265319 1,340096 1,418519 1,500730 1,586874 1,677100 1,771561
7 1,072135 1,148686 1,229874 1,315932 1,407100 1,503630 1,605781 1,713824 1,828039 1,948717
8 1,082857 1,171659 1,266770 1,368569 1,477455 1,593848 1,718186 1,850930 1,992563 2,143589
9 1,093685 1,195093 1,304773 1,423312 1,551328 1,689479 1,838459 1,999005 2,171893 2,357948
10 1,104622 1,218994 1,343916 1,480244 1,628895 1,790848 1,967151 2,158925 2,367364 2,593742
11 1,115668 1,243374 1,384234 1,539454 1,710339 1,898299 2,104852 2,331639 2,580426 2,853117
12 1,126825 1,268242 1,425761 1,601032 1,795856 2,012196 2,252192 2,518170 2,812665 3,138428
13 1,138093 1,293607 1,468534 1,665074 1,885649 2,132928 2,409845 2,719624 3,065805 3,452271
14 1,149474 1,319479 1,512590 1,731676 1,979932 2,260904 2,578534 2,937194 3,341727 3,797498
15 1,160969 1,345868 1,557967 1,800944 2,078928 2,396558 2,759032 3,172169 3,642482 4,177248
16 1,172579 1,372786 1,604706 1,872981 2,182875 2,540352 2,952164 3,425943 3,970306 4,594973
17 1,184304 1,400241 1,652848 1,947900 2,292018 2,692773 3,158815 3,700018 4,327633 5,054470
18 1,196147 1,428246 1,702433 2,025817 2,406619 2,854339 3,379932 3,996019 4,717120 5,559917
19 1,208109 1,456811 1,753506 2,106849 2,526950 3,025600 3,616528 4,315701 5,141661 6,115909
20 1,220190 1,485947 1,806111 2,191123 2,653298 3,207135 3,869684 4,660957 5,604411 6,727500
21 1,232392 1,515666 1,860295 2,278768 2,785963 3,399564 4,140562 5,033834 6,108808 7,400250
22 1,244716 1,545980 1,916103 2,369919 2,925261 3,603537 4,430402 5,436540 6,658600 8,140275
23 1,257163 1,576899 1,973587 2,464716 3,071524 3,819750 4,740530 5,871464 7,257874 8,954302
24 1,269735 1,608437 2,032794 2,563304 3,225100 4,048935 5,072367 6,341181 7,911083 9,849733
25 1,282432 1,640606 2,093778 2,665836 3,386355 4,291871 5,427433 6,848475 8,623081 10,83470
26 1,295256 1,673418 2,156591 2,772470 3,555673 4,549383 5,807353 7,396353 9,399158 11,91817
27 1,308209 1,706886 2,221289 2,883369 3,733456 4,822346 6,213868 7,988061 10,24508 13,10999
28 1,321291 1,741024 2,287928 2,998703 3,920129 5,111687 6,648838 8,627106 11,16714 14,42099
29 1,334504 1,775845 2,356566 3,118651 4,116136 5,418388 7,114257 9,317275 12,17218 15,86309
30 1,347849 1,811362 2,427262 3,243398 4,321942 5,743491 7,612255 10,06265 13,26767 17,44940
31 1,361327 1,847589 2,500080 3,373133 4,538039 6,088101 8,145113 10,86766 14,46177 19,19434
32 1,374941 1,884541 2,575083 3,508059 4,764941 6,453387 8,715271 11,73708 15,76332 21,11377
33 1,388690 1,922231 2,652335 3,648381 5,003189 6,840590 9,325340 12,67605 17,18202 23,22515
34 1,402577 1,960676 2,731905 3,794316 5,253348 7,251025 9,978114 13,69013 18,72841 25,54767
35 1,416603 1,999890 2,813862 3,946089 5,516015 7,686087 10,67658 14,78534 20,41396 28,10243
36 1,430769 2,039887 2,898278 4,103933 5,791816 8,147252 11,42394 15,96817 22,25122 30,91268
42 1,518790 2,297244 3,460696 5,192784 7,761588 11,55703 17,14425 25,33948 37,31753 54,76369
48 1,612226 2,587070 4,132252 6,570528 10,40127 16,39387 25,72890 40,21057 62,58523 97,01723
54 1,711410 2,913461 4,934125 8,313814 13,93869 23,25502 38,61215 63,80912 104,9617 171,8719
60 1,816697 3,281031 5,891603 10,51962 18,67918 32,98769 57,94642 101,2570 176,0312 304,4816


58

VALOR PRESENTE DE UMA SÉRIE UNIFORME IMEDIATA
n 1,0% 2,0% 3,0% 4,0% 5,0% 6,0% 7,0% 8,0% 9,0% 10,0%
1 0,990099 0,980392 0,970874 0,961538 0,952381 0,943396 0,934579 0,925926 0,917431 0,909091
2 1,970395 1,941561 1,913470 1,886095 1,859410 1,833393 1,808018 1,783265 1,759111 1,735537
3 2,940985 2,883883 2,828611 2,775091 2,723248 2,673012 2,624316 2,577097 2,531295 2,486852
4 3,901966 3,807729 3,717098 3,629895 3,545951 3,465106 3,387211 3,312127 3,239720 3,169865
5 4,853431 4,713460 4,579707 4,451822 4,329477 4,212364 4,100197 3,992710 3,889651 3,790787
6 5,795476 5,601431 5,417191 5,242137 5,075692 4,917324 4,766540 4,622880 4,485919 4,355261
7 6,728195 6,471991 6,230283 6,002055 5,786373 5,582381 5,389289 5,206370 5,032953 4,868419
8 7,651678 7,325481 7,019692 6,732745 6,463213 6,209794 5,971299 5,746639 5,534819 5,334926
9 8,566018 8,162237 7,786109 7,435332 7,107822 6,801692 6,515232 6,246888 5,995247 5,759024
10 9,471305 8,982585 8,530203 8,110896 7,721735 7,360087 7,023582 6,710081 6,417658 6,144567
11 10,36762 9,786848 9,252624 8,760477 8,306414 7,886875 7,498674 7,138964 6,805191 6,495061
12 11,25507 10,57534 9,954004 9,385074 8,863252 8,383844 7,942686 7,536078 7,160725 6,813692
13 12,13374 11,34837 10,63495 9,985648 9,393573 8,852683 8,357651 7,903776 7,486904 7,103356
14 13,00370 12,10624 11,29607 10,56312 9,898641 9,294984 8,745468 8,244237 7,786150 7,366687
15 13,86505 12,84926 11,93793 11,11838 10,37965 9,712249 9,107914 8,559479 8,060688 7,606080
16 14,71787 13,57770 12,56110 11,65229 10,83777 10,10589 9,446649 8,851369 8,312558 7,823709
17 15,56225 14,29187 13,16611 12,16566 11,27406 10,47726 9,763223 9,121638 8,543631 8,021553
18 16,39826 14,99203 13,75351 12,65929 11,68958 10,82760 10,05908 9,371887 8,755625 8,201412
19 17,22600 15,67846 14,32379 13,13393 12,08532 11,15811 10,33559 9,603599 8,950115 8,364920
20 18,04555 16,35143 14,87747 13,59032 12,46221 11,46992 10,59401 9,818147 9,128546 8,513564
21 18,85698 17,01120 15,41502 14,02916 12,82115 11,76407 10,83552 10,01680 9,292244 8,648694
22 19,66037 17,65804 15,93691 14,45111 13,16300 12,04158 11,06124 10,20074 9,442425 8,771540
23 20,45582 18,29220 16,44360 14,85684 13,48857 12,30337 11,27218 10,37105 9,580207 8,883218
24 21,24338 18,91392 16,93554 15,24696 13,79864 12,55035 11,46933 10,52875 9,706612 8,984744
25 22,02315 19,52345 17,41314 15,62208 14,09394 12,78335 11,65358 10,67477 9,822580 9,077040
26 22,79520 20,12103 17,87684 15,98276 14,37518 13,00316 11,82577 10,80997 9,928972 9,160945
27 23,55960 20,70689 18,32703 16,32958 14,64303 13,21053 11,98670 10,93516 10,02658 9,237223
28 24,31644 21,28127 18,76410 16,66306 14,89812 13,40616 12,13711 11,05107 10,11612 9,306567
29 25,06578 21,84438 19,18845 16,98371 15,14107 13,59072 12,27767 11,15840 10,19828 9,369606
30 25,80770 22,39645 19,60044 17,29203 15,37245 13,76483 12,40904 11,25778 10,27365 9,426914
31 26,54228 22,93770 20,00042 17,58849 15,59281 13,92908 12,53181 11,34979 10,34280 9,479013
32 27,26958 23,46833 20,38876 17,87355 15,80267 14,08404 12,64655 11,43499 10,40624 9,526376
33 27,98969 23,98856 20,76579 18,14764 16,00254 14,23023 12,75379 11,51388 10,46444 9,569432
34 28,70266 24,49859 21,13183 18,41119 16,19290 14,36814 12,85400 11,58693 10,51783 9,608575
35 29,40858 24,99861 21,48722 18,66461 16,37419 14,49824 12,94767 11,65456 10,56682 9,644159
36 30,10750 25,48884 21,83225 18,90828 16,54685 14,62098 13,03520 11,71719 10,61176 9,676508
42 34,15810 28,23479 23,70135 20,18562 17,42320 15,22454 13,45244 12,00669 10,81336 9,817397
48 37,97395 30,67312 25,26670 21,19513 18,07715 15,65002 13,73047 12,18913 10,93357 9,896926
54 41,56866 32,83828 26,57766 21,99295 18,56514 15,94997 13,91573 12,30410 11,00525 9,941817
60 44,95503 34,76088 27,67556 22,62349 18,92929 16,16142 14,03918 12,37655 11,04799 9,967157


59

VALOR FUTURO DE UMA SÉRIE UNIFORME IMEDIATA
n 1,0% 2,0% 3,0% 4,0% 5,0% 6,0% 7,0% 8,0% 9,0% 10,0%
1 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000
2 2,010000 2,020000 2,030000 2,040000 2,050000 2,060000 2,070000 2,080000 2,090000 2,100000
3 3,030100 3,060400 3,090900 3,121600 3,152500 3,183600 3,214900 3,246400 3,278100 3,310000
4 4,060401 4,121608 4,183627 4,246464 4,310125 4,374616 4,439943 4,506112 4,573129 4,641000
5 5,101005 5,204040 5,309136 5,416323 5,525631 5,637093 5,750739 5,866601 5,984711 6,105100
6 6,152015 6,308121 6,468410 6,632975 6,801913 6,975319 7,153291 7,335929 7,523335 7,715610
7 7,213535 7,434283 7,662462 7,898294 8,142008 8,393838 8,654021 8,922803 9,200435 9,487171
8 8,285671 8,582969 8,892336 9,214226 9,549109 9,897468 10,25980 10,63662 11,02847 11,43588
9 9,368527 9,754628 10,15910 10,58279 11,02656 11,49131 11,97798 12,48755 13,02103 13,57947
10 10,46221 10,94972 11,46387 12,00610 12,57789 13,18079 13,81644 14,48656 15,19293 15,937425
11 11,56683 12,16871 12,80779 13,48635 14,20678 14,97164 15,78359 16,64548 17,56029 18,531167
12 12,68250 13,41209 14,19203 15,02580 15,91712 16,86994 17,88845 18,97712 20,14072 21,384284
13 13,80932 14,68033 15,61779 16,62683 17,71298 18,88213 20,14064 21,49529 22,95338 24,522712
14 14,94742 15,97393 17,08632 18,29191 19,59863 21,01506 22,55048 24,21492 26,01918 27,974983
15 16,09689 17,29341 18,59891 20,02358 21,57856 23,27597 25,12902 27,15211 29,36091 31,772482
16 17,25786 18,63928 20,15688 21,82453 23,65749 25,67252 27,88805 30,32428 33,00339 35,949730
17 18,43044 20,01207 21,76158 23,69751 25,84036 28,21288 30,84021 33,75022 36,97370 40,544703
18 19,61474 21,41231 23,41443 25,64541 28,13238 30,90565 33,99903 37,45024 41,30133 45,599173
19 20,81089 22,84055 25,11686 27,67122 30,53900 33,75999 37,37896 41,44626 46,01845 51,159090
20 22,01900 24,29737 26,87037 29,77807 33,06595 36,78559 40,99549 45,76196 51,16012 57,274999
21 23,23919 25,78331 28,67648 31,96920 35,71925 39,99272 44,86517 50,42292 56,76453 64,002499
22 24,47158 27,29898 30,53678 34,24797 38,50521 43,39229 49,00573 55,45675 62,87333 71,402749
23 25,71630 28,84496 32,45288 36,61788 41,43047 46,99582 53,43614 60,89329 69,53193 79,543024
24 26,97346 30,42186 34,42647 39,08260 44,50199 50,81557 58,17667 66,76475 76,78981 88,497327
25 28,24320 32,03030 36,45926 41,64590 47,72709 54,86451 63,24903 73,10594 84,70089 98,347059
26 29,52563 33,67090 38,55304 44,31174 51,11345 59,15638 68,67647 79,95441 93,32397 109,18176
27 30,82088 35,34432 40,70963 47,08421 54,66912 63,70576 74,48382 87,35076 102,7231 121,09994
28 32,12909 37,05121 42,93092 49,96758 58,40258 68,52811 80,69769 95,33883 112,9682 134,20993
29 33,45038 38,79223 45,21885 52,96628 62,32271 73,63979 87,34652 103,9659 124,1353 148,63093
30 34,78489 40,56807 47,57541 56,08493 66,43884 79,05818 94,46078 113,2832 136,3075 164,49402
31 36,13274 42,37944 50,00267 59,32833 70,76079 84,80167 102,0730 123,3458 149,5752 181,94342
32 37,49406 44,22703 52,50275 62,70146 75,29882 90,88977 110,2181 134,2135 164,0369 201,13776
33 38,86900 46,11157 55,07784 66,20952 80,06377 97,34316 118,9334 145,9506 179,8003 222,25154
34 40,25769 48,03380 57,73017 69,85790 85,06695 104,1837 128,2587 158,6266 196,9823 245,47669
35 41,66027 49,99447 60,46208 73,65222 90,32030 111,4347 138,2368 172,3168 215,7107 271,02436
36 43,07687 51,99436 63,27594 77,59831 95,83632 119,1208 148,9134 187,1021 236,1247 299,12680
42 51,87898 64,86222 82,02319 104,8195 135,2317 175,9505 230,6322 304,2435 403,5281 37,636992
48 61,22260 79,35351 104,4083 139,2632 188,0253 256,5645 353,2700 490,1321 684,2804 960,17233
54 71,14104 95,67307 131,1374 182,8453 258,7739 370,9170 537,3164 785,1140 1155,130 1708,7194
60 81,66967 114,0515 163,0534 237,9906 353,5837 533,1281 813,5203 1253,213 1944,792 3034,8163


60

FATOR DE CONVERSÃO DE SÉRIE GRADIENTE PARA IMEDIATA
n 1,0% 2,0% 3,0% 4,0% 5,0% 6,0% 7,0% 8,0% 9,0% 10,0%
2 0,497512 0,495050 0,492611 0,490196 0,487805 0,485437 0,483092 0,480769 0,478469 0,476190
3 0,993367 0,986799 0,980297 0,973860 0,967486 0,961176 0,954929 0,948743 0,942619 0,936556
4 1,487562 1,475249 1,463061 1,450995 1,439053 1,427234 1,415536 1,403960 1,392504 1,381168
5 1,980100 1,960401 1,940905 1,921611 1,902520 1,883633 1,864950 1,846472 1,828197 1,810126
6 2,470980 2,442256 2,413833 2,385715 2,357904 2,330404 2,303217 2,276346 2,249792 2,223557
7 2,960202 2,920815 2,881851 2,843318 2,805225 2,767581 2,730392 2,693665 2,657404 2,621615
8 3,447766 3,396080 3,344963 3,294434 3,244510 3,195208 3,146541 3,098524 3,051166 3,004479
9 3,933673 3,868053 3,803176 3,739077 3,675786 3,613331 3,551740 3,491033 3,431231 3,372351
10 4,417923 4,336736 4,256498 4,177264 4,099085 4,022007 3,946071 3,871314 3,797768 3,725461
11 4,900517 4,802131 4,704936 4,609014 4,514444 4,421295 4,329629 4,239503 4,150964 4,064054
12 5,381454 5,264242 5,148499 5,034348 4,921902 4,811261 4,702516 4,595747 4,491023 4,388402
13 5,860734 5,723071 5,587198 5,453288 5,321501 5,191977 5,064842 4,940207 4,818164 4,698792
14 6,338360 6,178621 6,021042 5,865859 5,713289 5,563521 5,416727 5,273051 5,132618 4,995529
15 6,814330 6,630896 6,450043 6,272087 6,097314 5,925976 5,758295 5,594460 5,434631 5,278933
16 7,288645 7,079899 6,874214 6,672000 6,473629 6,279428 6,089681 5,904626 5,724460 5,549341
17 7,761306 7,525635 7,293567 7,065628 6,842292 6,623972 6,411025 6,203746 6,002375 5,807097
18 8,232314 7,968108 7,708116 7,453002 7,203360 6,959705 6,722474 6,492028 6,268653 6,052560
19 8,701668 8,407322 8,117876 7,834156 7,556896 7,286728 7,024182 6,769688 6,523580 6,286095
20 9,169370 8,843282 8,522862 8,209125 7,902965 7,605148 7,316307 7,036948 6,767450 6,508075
21 9,635420 9,275993 8,923090 8,577945 8,241635 7,915075 7,599014 7,294034 7,000563 6,718878
22 10,09981 9,705459 9,318577 8,940654 8,572976 8,216625 7,872471 7,541181 7,223224 6,918886
23 10,56256 10,13168 9,709341 9,297292 8,897062 8,509914 8,136853 7,778626 7,435742 7,108483
24 11,02366 10,55468 10,09540 9,647901 9,213968 8,795065 8,392336 8,006612 7,638428 7,288054
25 11,48311 10,97445 10,47677 9,992523 9,523771 9,072201 8,639101 8,225382 7,831597 7,457982
26 11,94091 11,39100 10,85348 10,33120 9,826553 9,341450 8,877332 8,435184 8,015563 7,618650
27 12,39707 11,80433 11,22554 10,66398 10,12239 9,602942 9,107217 8,636268 8,190639 7,770437
28 12,85158 12,21446 11,59298 10,99091 10,41138 9,856809 9,328943 8,828883 8,357141 7,913716
29 13,30444 12,62138 11,95581 11,31204 10,69360 10,10318 9,542701 9,013281 8,515378 8,048858
30 13,75566 13,02511 12,31407 11,62742 10,96913 10,34221 9,748684 9,189712 8,665661 8,176226
31 14,20523 13,42566 12,66777 11,93710 11,23808 10,57402 9,947084 9,358427 8,808293 8,296174
32 14,65316 13,82302 13,01694 12,24112 11,50053 10,79875 10,13809 9,519675 8,943578 8,409051
33 15,09945 14,21722 13,36159 12,53955 11,75657 11,01655 10,32191 9,673702 9,071812 8,515196
34 15,54410 14,60825 13,70177 12,83244 12,00629 11,22755 10,49872 9,820753 9,193286 8,614940
35 15,98711 14,99613 14,03749 13,11984 12,24980 11,43191 10,66873 9,961072 9,308285 8,708603
36 16,42848 15,38086 14,36878 13,40181 12,48719 11,62976 10,83212 10,09489 9,417091 8,796497
42 19,04237 17,62368 16,26499 14,98278 13,78844 12,68827 11,68417 10,77440 9,954645 9,218804
48 21,59759 19,75559 18,00889 16,38322 14,89430 13,54854 12,34466 11,27584 10,33170 9,500090
54 24,09445 21,77889 19,60728 17,61671 15,82647 14,24024 12,85000 11,64025 10,59168 9,683974
60 26,53331 23,69610 21,06741 18,69723 16,60617 14,79094 13,23209 11,90153 10,76831 9,802294


61

TABELA PARA CONTAGEM DE DIAS ENTRE DATAS
Dias Jan Fev Mar Abr Mai Jun Jul Ago Set Out Nov Dez Dias

1 1 32 60 91 121 152 182 213 244 274 305 335 1
2 2 33 61 92 122 153 183 214 245 275 306 336 2
3 3 34 62 93 123 154 184 215 246 276 307 337 3
4 4 35 63 94 124 155 185 216 247 277 308 338 4
5 5 36 64 95 125 156 186 217 248 278 309 339 5
6 6 37 65 96 126 157 187 218 249 279 310 340 6
7 7 38 66 97 127 158 188 219 250 280 311 341 7
8 8 39 67 98 128 159 189 220 251 281 312 342 8
9 9 40 68 99 129 160 190 221 252 282 313 343 9
10 10 41 69 100 130 161 191 222 253 283 314 344 10
11 11 42 70 101 131 162 192 223 254 284 315 345 11
12 12 43 71 102 132 163 193 224 255 285 316 346 12
13 13 44 72 103 133 164 194 225 256 286 317 347 13
14 14 45 73 104 134 165 195 226 257 287 318 348 14
15 15 46 74 105 135 166 196 227 258 288 319 349 15
16 16 47 75 106 136 167 197 228 259 289 320 350 16
17 17 48 76 107 137 168 198 229 260 290 321 351 17
18 18 49 77 108 138 169 199 230 261 291 322 352 18
19 19 50 78 109 139 170 200 231 262 292 323 353 19
20 20 51 79 110 140 171 201 232 263 293 324 354 20
21 21 52 80 111 141 172 202 233 264 294 325 355 21
22 22 53 81 112 142 173 203 234 265 295 326 356 22
23 23 54 82 113 143 174 204 235 266 296 327 357 23
24 24 55 83 114 144 175 205 236 267 297 328 358 24
25 25 56 84 115 145 176 206 237 268 298 329 359 25
26 26 57 85 116 146 177 207 238 269 299 330 360 26
27 27 58 86 117 147 178 208 239 270 300 331 361 27
28 28 59 87 118 148 179 209 240 271 301 332 362 28
29 29 88 119 149 180 210 241 272 302 333 363 29
30 30 89 120 150 181 211 242 273 303 334 364 30
31 31 90 151 212 243 304 365 31


62

BIBLIOGRAFIA

ASSAF NETO, Alexandre. Matemática financeira e suas aplicações. São Paulo,
Atlas, 1997.

AYRES JR., Frank. Matemática financeira. São Paulo, McGraw-Hill do Brasil,
1971.

CANTELLI, Francesco Paolo. Sui fondamenti della matematica finanziaria.
Torino, Giornale di Matematica Finanziaria, 1941.

CLEMENTE, Ademir (organizador). Projetos empresariais e públicos. São paulo,
Atlas, 1998.

DOWSLEY, Getúlio dos Santos. Administração financeira e economia
empresarial. Rio de Janeiro, LTC, 1989.

FARIA, Rogério Gomes de. Matemática financeira. São Paulo, Makron Books,
2000.

FARO, Clovis de. Matemática financeira. Rio de Janeiro, APEC, 1974.

FORTUNA, Eduardo. Mercado financeiro: produtos e serviços. Rio de Janeiro,
Qualitymark, 1998.

FRANCISCO, Walter de. Matemática financeira. São Paulo, Atlas, 1991.

HAZZAN, Samuel; POMPEO, José Nicolau. Matemática financeira. São Paulo,
Saraiva, 2001.

HESS, Geraldo; MARQUES, José Luiz; PAES, L. C. Rocha; PUCCINI, Abelardo.
Engenharia econômica: cem tabelas de juros impressas em computador. Rio
de Janeiro, Bertrand Brasil, 1988.

HUMMEL, Paulo Roberto Vampré; TASCHNER, Mauro Roberto Black. Análise e
decisão sobre investimentos e financiamentos: engenharia econômica – teoria
e prática. São paulo, Atlas, 1988.

LAUREANO, José Luiz Tavares & LEITE, Olímpio Rudinin Vissoto. Os segredos da
matemática financeira. São Paulo, Ática, 1994.

MARTINS, Eliseu. Contabilidade de custos. São paulo, Atlas, 1998.

MATIAS, Washington Franco & GOMES, José Maria. Matemática financeira. São
Paulo, Atlas, 1992.

MELLAGI FILHO, Armando. Mercado financeiro e de capitais: uma introdução.
São Paulo, Atlas, 1995.

PUCCINI, Abelardo de Lima. Matemática financeira: objetiva e aplicada. São
Paulo, Saraiva, 1999.


63

RUDGE, Luiz Fernando; CAVALCANTE, Francisco. Mercado de capitais. Belo
Horizonte, CNBV, 1998.

SAMANEZ, Carlos Patricio. Matemática financeira: aplicações à análise de
investimentos. São Paulo, Prentice Hall, 2001.

SILVA, Sérgio Eduardo Dias da. Gerência financeira: a empresa e seu
relacionamento com os bancos. São Paulo, Saraiva, 1991.

SOUZA, Alceu; CLEMENTE, Ademir. Decisões financeiras e análise de
investimentos: fundamentos, técnicas e aplicações. São Paulo, Atlas, 1995.

SOUZA, Alceu; CLEMENTE, Ademir. Matemática financeira: fundamentos,
conceitos, aplicações. São Paulo, Atlas, 1999.

VERAS, Lilia Ladeira. Matemática Financeira: uso de calculadoras financeiras:
aplicações ao mercado financeiro: introdução à engenharia econômica: 300
exercícios resolvidos e propostos com respostas. São Paulo, Atlas, 1989.

VIEIRA SOBRINHO, José Dutra. Manual de Aplicações Financeiras: HP 12-C:
Adaptável às calculadoras HP - 38 E/C. São Paulo, Atlas, 1985.


Curso mat financeira

Mais conteúdo relacionado

Mais procurados

Semelhante a Curso mat financeira

Curso mat financeira