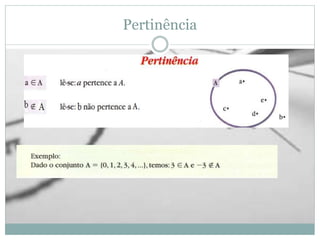
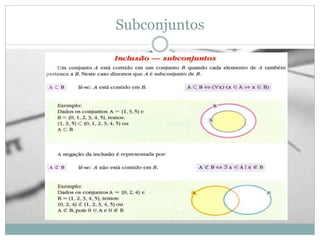
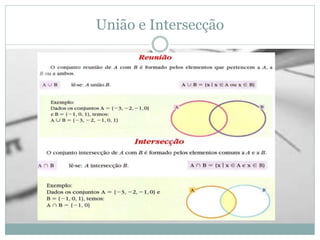
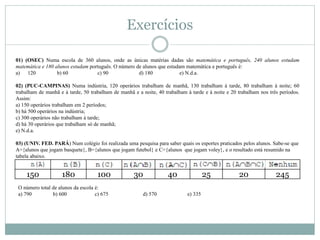
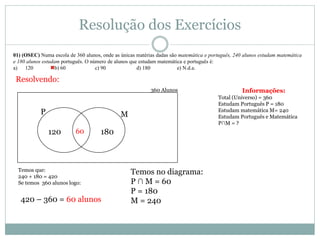
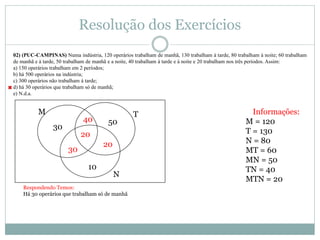
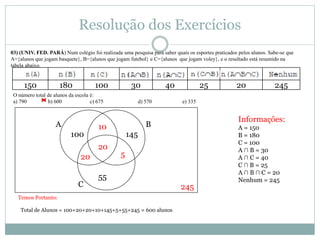
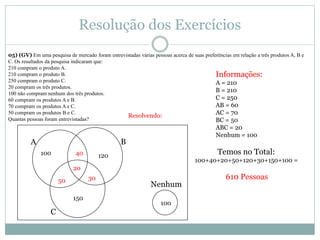
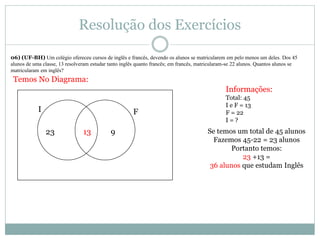
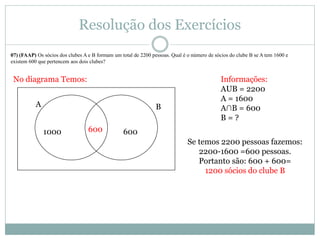
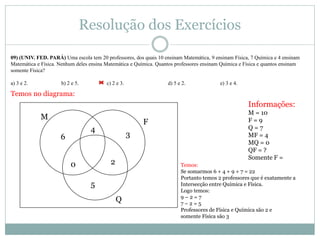
O documento apresenta os conceitos básicos de conjuntos, incluindo definição de conjunto e elemento, pertinência, igualdade, representação, conjuntos vazio, unitário e universo, subconjuntos, pertinências, diferença e complementar, união e intersecção. Exemplos e exercícios são fornecidos para praticar esses conceitos.

1. Conjuntos
Colégio São Francisco de Assis Anápolis 2012
Professora:
Ana Lídia Sena

2. Definição
Conjunto: representa uma coleção de objetos, geralmente representado por
letras maiúsculas;
Elemento: qualquer um dos componentes de um conjunto, geralmente
representado por letras minúsculas. Um elemento pode pertencer ou não a
um conjunto ( )
As noções primitivas de conjunto, elemento
e pertinência tem sua origem nos trabalhos
do matemático russo Georg Cantor (1845 –
1918)

3. Pertinência

4. Igualdade

5. RepresentaçãoRepresentação

6. Conjuntos vazio, unitário e universo
 Conjunto vazio
É o conjunto que não possui elementos.
Representação: { } ou Ø
 Conjunto Unitário
É o conjunto formado por um único elemento.
Exemplos: { a }, { b}
 Conjunto Universo
É o conjunto formado por todos os elementos de
um assunto trabalhado.
Representação: U

7. Vamos praticar!
Atividades página 2

8. Subconjuntos

9. Pertinências
 Pertence ou não pertence ( )
É usado entre elemento e conjunto.
 Contido ou não contido ( )
É usado entre subconjunto e conjunto.
 Contém e não contém ( )
É usado entre conjunto e subconjunto.

10. Vamos praticar!
Atividades páginas 3 e 4

11. Diferença e ComplementarDiferença e Complementar

12. União e IntersecçãoUnião e Intersecção

13. Exercícios
01) (OSEC) Numa escola de 360 alunos, onde as únicas matérias dadas são matemática e português, 240 alunos estudam
matemática e 180 alunos estudam português. O número de alunos que estudam matemática e português é:
a) 120 b) 60 c) 90 d) 180 e) N.d.a.
02) (PUC-CAMPINAS) Numa indústria, 120 operários trabalham de manhã, 130 trabalham à tarde, 80 trabalham à noite; 60
trabalham de manhã e à tarde, 50 trabalham de manhã e a noite, 40 trabalham à tarde e à noite e 20 trabalham nos três períodos.
Assim:
a) 150 operários trabalham em 2 períodos;
b) há 500 operários na indústria;
c) 300 operários não trabalham à tarde;
d) há 30 operários que trabalham só de manhã;
e) N.d.a.
03) (UNIV. FED. PARÁ) Num colégio foi realizada uma pesquisa para saber quais os esportes praticados pelos alunos. Sabe-se que
A={alunos que jogam basquete}, B={alunos que jogam futebol} e C={alunos que jogam voley}, e o resultado está resumido na
tabela abaixo.
150 180 100 30 40 25 20 245
O número total de alunos da escola é:
a) 790 b) 600 c) 675 d) 570 e) 335

14. 04) (CESGRANRIO) Em uma universidade são lidos dois jornais A e B; exatamente 80% dos alunos lêem o jornal A e 60% o jornal B.
Sabendo-se que todo aluno é leitor de pelo menos um dos jornais, o percentual de alunos que lêem ambos é:
a) 48% b) 60% c) 40% d) 140% e) 80%
05) (GV) Em uma pesquisa de mercado foram entrevistadas várias pessoas acerca de suas preferências em relação a três produtos A, B
e C. Os resultados da pesquisa indicaram que:
210 compram o produto A.
210 compram o produto B.
250 compram o produto C.
20 compram os três produtos.
100 não compram nenhum dos três produtos.
60 compram os produtos A e B.
70 compram os produtos A e C.
50 compram os produtos B e C.
Quantas pessoas foram entrevistadas?
06) (UF-BH) Um colégio ofereceu cursos de inglês e francês, devendo os alunos se matricularem em pelo menos um deles. Dos 45
alunos de uma classe, 13 resolveram estudar tanto inglês quanto francês; em francês, matricularam-se 22 alunos. Quantos alunos se
matricularam em inglês?
Exercícios

15. 07) (FAAP) Os sócios dos clubes A e B formam um total de 2200 pessoas. Qual é o número de sócios do clube B se A tem 1600 e existem
600 que pertencem aos dois clubes?
08) (MED. RIO PRETO) Num almoço, foram servidos, entre outros pratos, frangos e leitões. Sabendo-se que, das 94 pessoas presente, 56
comeram frango, 41 comeram leitão e 21 comeram dos dois, o número de pessoas que não comeram nem frango nem leitão é:
a) 10 b) 12 c) 15 d) 17 e) 18
09) (UNIV. FED. PARÁ) Uma escola tem 20 professores, dos quais 10 ensinam Matemática, 9 ensinam Física, 7 Química e 4 ensinam
Matemática e Física. Nenhum deles ensina Matemática e Química. Quantos professores ensinam Química e Física e quantos ensinam
somente Física?
a) 3 e 2. b) 2 e 5. c) 2 e 3. d) 5 e 2. e) 3 e 4.
Exercícios

16. Resolução dos Exercícios
01) (OSEC) Numa escola de 360 alunos, onde as únicas matérias dadas são matemática e português, 240 alunos estudam matemática
e 180 alunos estudam português. O número de alunos que estudam matemática e português é:
a) 120 b) 60 c) 90 d) 180 e) N.d.a.
Resolvendo:
Informações:
Total (Universo) = 360
Estudam Português P = 180
Estudam matemática M= 240
Estudam Português e Matemática
P∩M = ?
360 Alunos
P M
Temos que:
240 + 180 = 420
Se temos 360 alunos logo:
420 – 360 = 60 alunos
Temos no diagrama:
P ∩ M = 60
P = 180
M = 240
60120 180

17. Resolução dos Exercícios
02) (PUC-CAMPINAS) Numa indústria, 120 operários trabalham de manhã, 130 trabalham à tarde, 80 trabalham à noite; 60 trabalham
de manhã e à tarde, 50 trabalham de manhã e a noite, 40 trabalham à tarde e à noite e 20 trabalham nos três períodos. Assim:
a) 150 operários trabalham em 2 períodos;
b) há 500 operários na indústria;
c) 300 operários não trabalham à tarde;
d) há 30 operários que trabalham só de manhã;
e) N.d.a.
Informações:
M = 120
T = 130
N = 80
MT = 60
MN = 50
TN = 40
MTN = 20
M
N
T
20
20
30
40
10
50
30
Respondendo Temos:
Há 30 operários que trabalham só de manhã

18. Resolução dos Exercícios
03) (UNIV. FED. PARÁ) Num colégio foi realizada uma pesquisa para saber quais os esportes praticados pelos alunos. Sabe-se que
A={alunos que jogam basquete}, B={alunos que jogam futebol} e C={alunos que jogam voley}, e o resultado está resumido na
tabela abaixo.
150 180 100 30 40 25 20 245
O número total de alunos da escola é:
a) 790 b) 600 c) 675 d) 570 e) 335
Informações:
A = 150
B = 180
C = 100
A ∩ B = 30
A ∩ C = 40
C ∩ B = 25
A ∩ B ∩ C = 20
Nenhum = 245
A
C
B
245
20
520
10
55
145100
Temos Portanto:
Total de Alunos = 100+20+20+10+145+5+55+245 = 600 alunos

19. Resolução dos Exercícios
04) (CESGRANRIO) Em uma universidade são lidos dois jornais A e B; exatamente 80% dos alunos lêem o jornal A e 60% o jornal B.
Sabendo-se que todo aluno é leitor de pelo menos um dos jornais, o percentual de alunos que lêem ambos é:
a) 48% b) 60% c) 40% d) 140% e) 80%
Informações:
Jornal A = 80%
Jornal B = 60%
A ∩ B = ?
Resolvendo:
Temos 80 + 60 = 140
Façamos agora : 140-100 = 40%
No diagrama temos:
A B
4040 20
Temos portanto o percentual de alunos
Que lêem ambos é 40%

20. Resolução dos Exercícios
05) (GV) Em uma pesquisa de mercado foram entrevistadas várias pessoas acerca de suas preferências em relação a três produtos A, B e
C. Os resultados da pesquisa indicaram que:
210 compram o produto A.
210 compram o produto B.
250 compram o produto C.
20 compram os três produtos.
100 não compram nenhum dos três produtos.
60 compram os produtos A e B.
70 compram os produtos A e C.
50 compram os produtos B e C.
Quantas pessoas foram entrevistadas?
Informações:
A = 210
B = 210
C = 250
AB = 60
AC = 70
BC = 50
ABC = 20
Nenhum = 100
Resolvendo:
A
C
Nenhum
B
100
20
3050
40
150
120100 Temos no Total:
100+40+20+50+120+30+150+100 =
610 Pessoas

21. Resolução dos Exercícios
06) (UF-BH) Um colégio ofereceu cursos de inglês e francês, devendo os alunos se matricularem em pelo menos um deles. Dos 45
alunos de uma classe, 13 resolveram estudar tanto inglês quanto francês; em francês, matricularam-se 22 alunos. Quantos alunos se
matricularam em inglês?
Informações:
Total: 45
I e F = 13
F = 22
I = ?
Temos No Diagrama:
I F
13 9 Se temos um total de 45 alunos
Fazemos 45-22 = 23 alunos
Portanto temos:
23 +13 =
36 alunos que estudam Inglês
23

22. Resolução dos Exercícios
07) (FAAP) Os sócios dos clubes A e B formam um total de 2200 pessoas. Qual é o número de sócios do clube B se A tem 1600 e
existem 600 que pertencem aos dois clubes?
Informações:
AUB = 2200
A = 1600
A∩B = 600
B = ?
No diagrama Temos:
A B
6001000
Se temos 2200 pessoas fazemos:
2200-1600 =600 pessoas.
Portanto são: 600 + 600=
1200 sócios do clube B
600

23. Resolução dos Exercícios
08) (MED. RIO PRETO) Num almoço, foram servidos, entre outros pratos, frangos e leitões. Sabendo-se que, das 94 pessoas presente,
56 comeram frango, 41 comeram leitão e 21 comeram dos dois, o número de pessoas que não comeram nem frango nem leitão é:
a) 10 b) 12 c) 15 d) 17 e) 18
Informações:
Total = 94
F = 56
L = 41
F ∩ L = 21
Nenhum =
Temos No diagrama:
F L
Nenhum
21 2035
Temos portanto:
94 – 76 = 18 pessoas
18
18

24. Resolução dos Exercícios
09) (UNIV. FED. PARÁ) Uma escola tem 20 professores, dos quais 10 ensinam Matemática, 9 ensinam Física, 7 Química e 4 ensinam
Matemática e Física. Nenhum deles ensina Matemática e Química. Quantos professores ensinam Química e Física e quantos ensinam
somente Física?
a) 3 e 2. b) 2 e 5. c) 2 e 3. d) 5 e 2. e) 3 e 4.
Informações:
M = 10
F = 9
Q = 7
MF = 4
MQ = 0
QF = ?
Somente F =
Temos no diagrama:
M
Q
F
4
0
6
Temos:
Se somarmos 6 + 4 + 9 + 7 = 22
Portanto temos 2 professores que é exatamente a
Intersecção entre Química e Física.
Logo temos:
9 – 2 = 7
7 – 2 = 5
Professores de Física e Química são 2 e
somente Física são 3
2
5
3