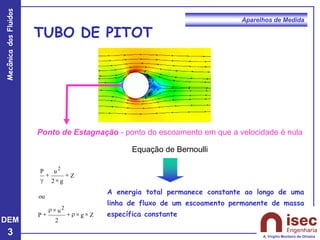
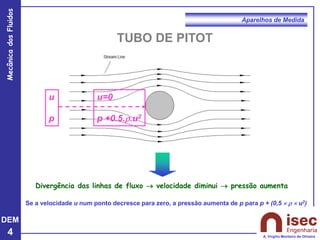
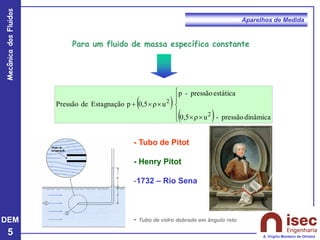
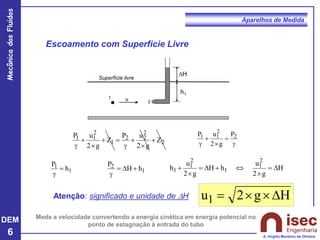
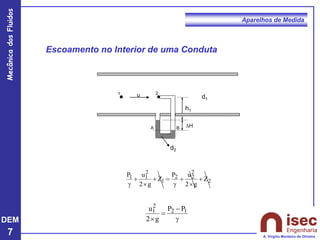
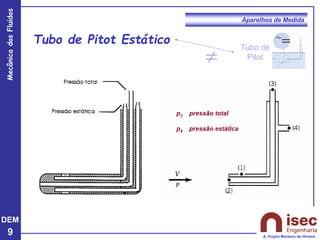
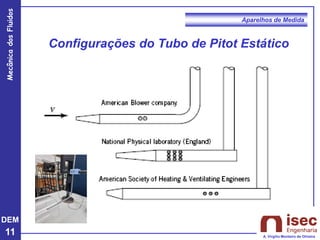
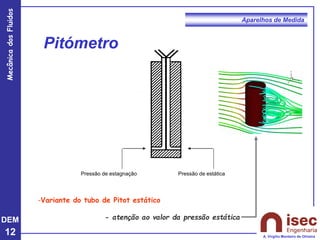
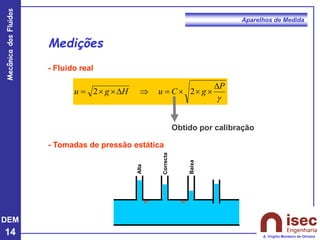
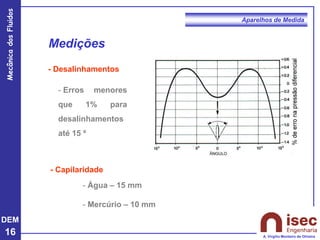
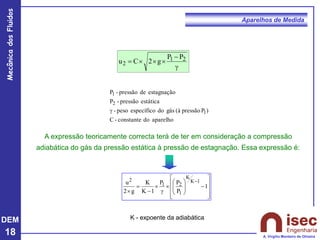
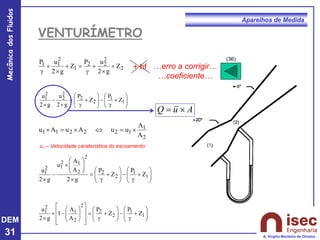
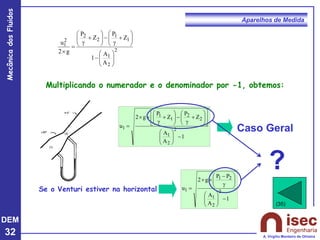
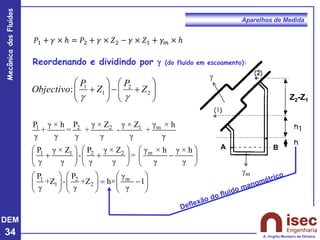
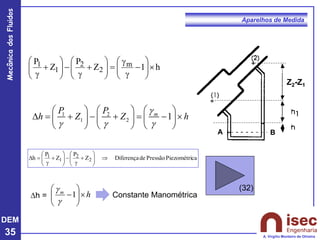
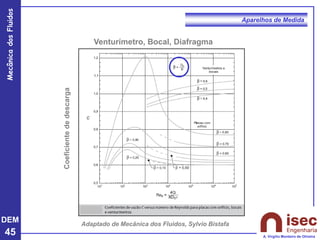
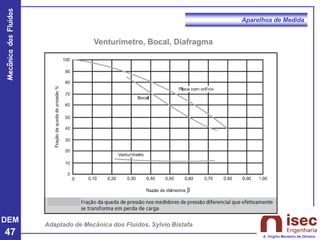
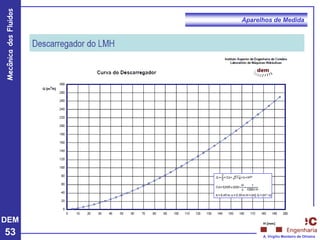
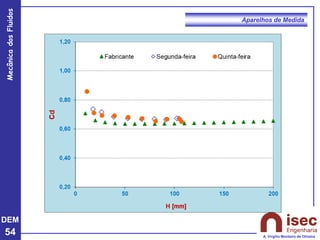
O documento apresenta conceitos fundamentais sobre a mecânica dos fluidos, focando em aparelhos de medida como o tubo de Pitot e venturi, utilizados para medir velocidade e pressão em escoamentos. Explora a equação de Bernoulli e as relações entre pressão, velocidade e altura em fluidos, tanto em escoamentos permanentes quanto em fluídos compressíveis. Além disso, menciona as vantagens e desvantagens do tubo de Pitot, incluindo suas aplicações práticas e relevância em acidentes aeronáuticos.