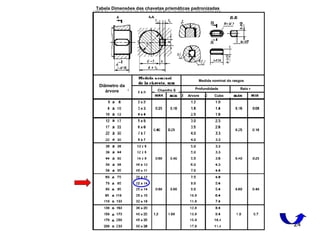
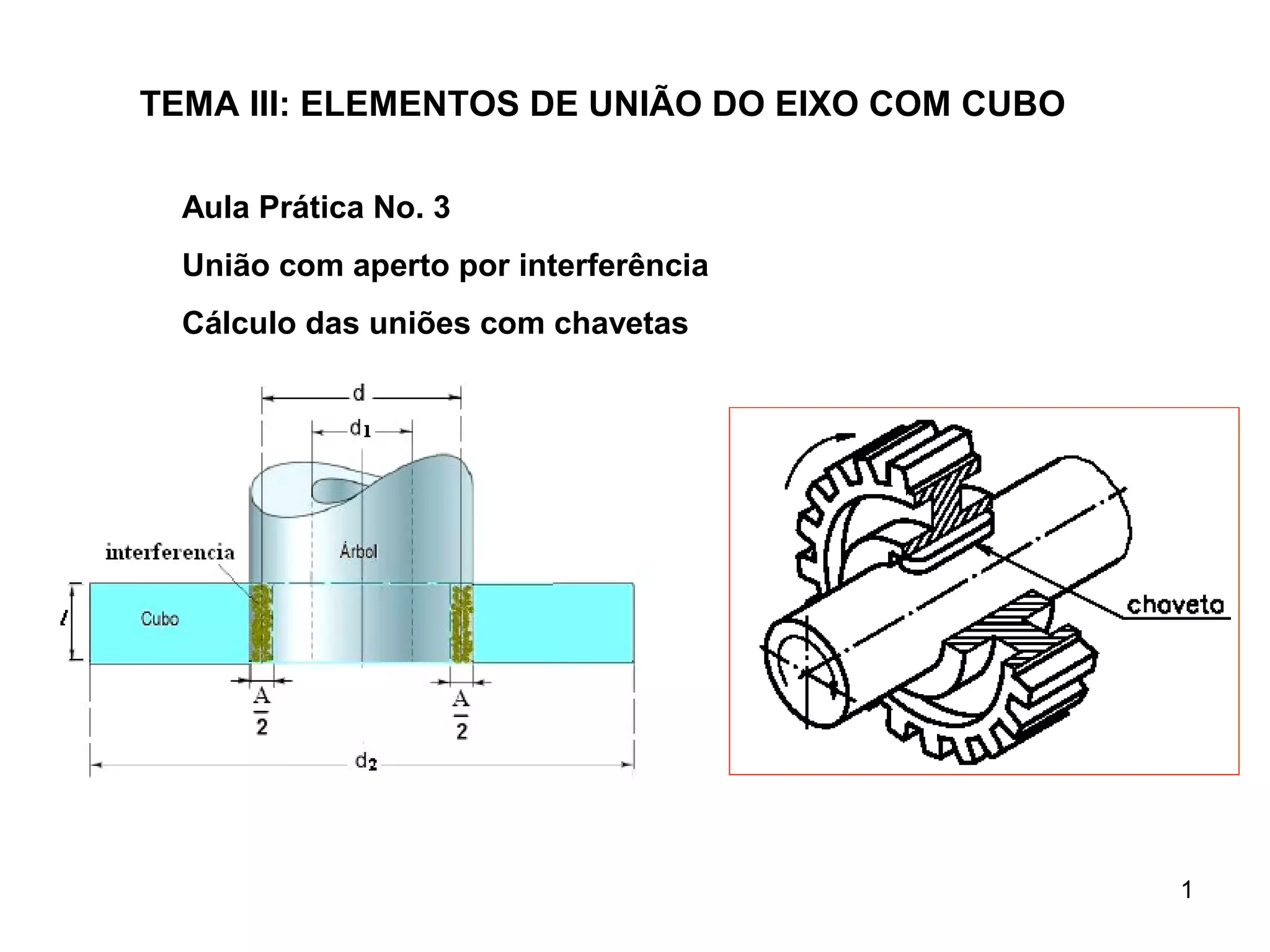
Este documento discute uniões por interferência e chavetas. Ele fornece fórmulas para calcular o aperto necessário em uniões por interferência e dimensionar chavetas. Também mostra como verificar a resistência destas uniões sob carga de torção considerando propriedades dos materiais.

1. 1
Aula Prática No. 3
União com aperto por interferência
Cálculo das uniões com chavetas
TEMA III: ELEMENTOS DE UNIÃO DO EIXO COM CUBO

2. 2
Tabela 2- Ajustes recomendados.
TABELAS IMPORTANTES PARA ESTE TEMA:

3. 3
TABELAS IMPORTANTES PARA ESTE TEMA:
Tabela 5 Valores da tolerância em µm.

4. 4

5. 5
Intervalo das
dimensões Afastamento superior do eixo – es (µm)
Furo Afastamento inferior do furo – EI (µm)

6. 6
1- Projete a união com aperto por interferência que se mostra na figura se tiverem os
seguintes dados:
Momento de torção máximo a transmitir é de 1400 Nm. Deve-se trabalhar com um fator
de segurança de 2. Coeficiente de atrito 0,14. Coeficiente de dilatação térmica 12x10-6
1/°C.
O eixo é de AISI 1010 com uma tensão de escoamento de 300 MPa e um módulo de
elasticidade de 2x105
MPa.
A roda é de AISI 1020 com uma tensão de escoamento de 360 MPa e um módulo de
elasticidade de 2x105
MPa.
Problema # 1

7. 7
Solução.
1.- Aperto necessário.
un
E
C
E
C
fl
Fa
d
T
Anec +





+
⋅⋅
+





= 3,
2
2
1
1
2
2
10.
2
π
T = 1 400 000 Nmm.
Fa = 0
d = 200 mm
l = 30 mm (comprimento do
cubo)
E1
= E2
= 2. 105
MPa. (açõs)
nl
= 2
f = 0.14
2,13,0
90200
90200
22
22
12
1
2
2
1
2
1 =−
−
+
=−
−
+
= µ
dd
dd
C
( ) .72,30)2,32,3(8,48,4)(2,1 2121 mRaRaRzRzu µ=+=+=+=

8. 8
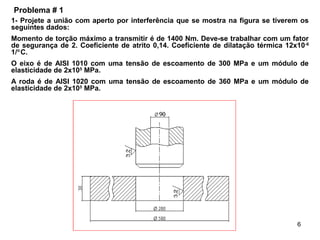
2.- Aperto máximo permissível.
[ ] 3
2
2
1
1
max 10
E
C
E
C
d.PA 





+=
Roda.
[ ]
2
2
22
2t
max
d2
)dd(
p
−σ
=
[ ] MPat y 3602 == σσ
MPap 2,151
)500(2
)200500(360
2
22
max =
−
=
Eixo.
[ ]
2
2
1
2
t
max
d2
)dd(
p
−σ
=
[ ] MPat y 3001 == σσ
MpaP 6,119
)200(2
)90200(300
2
22
max =
−
=
O eixo possui menor resistência.

9. 9
3.- Seleção do ajuste. (Sistema do furo base).
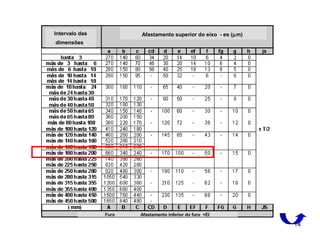
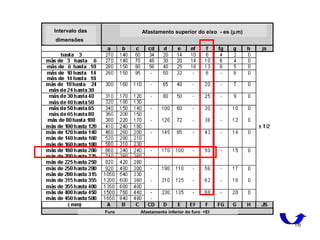
Ajuste: necmin AESeiA ≥−= = 61,27 µm
[ ]AEIesAmax ≤−= = 344,44 µm
ei ≥ Anec + ES
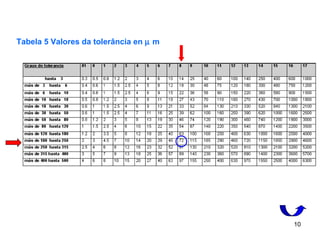
Considerando o grau de tolerância IT8 para o furo:
H8  EI = 0 e ES = T8
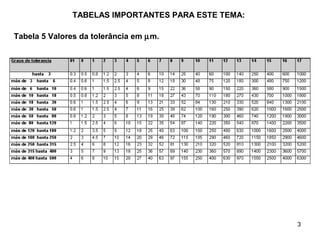
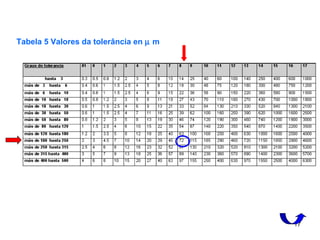
=72 µm (Tabela 5)
ei ≥ 61,27 + 72 = 133,27 µm
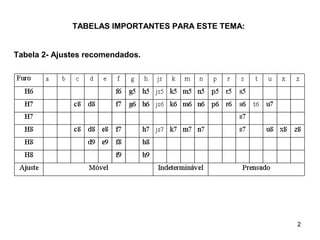
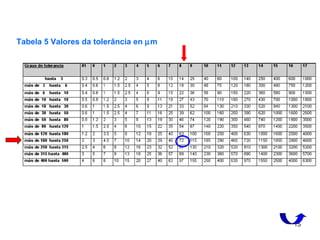
Ajustes recomendados (Tabela 2).
z8
H8
e,
x8
H8
,
u8
H8
,
s7
H8
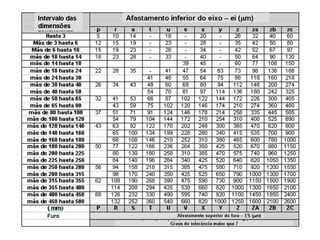
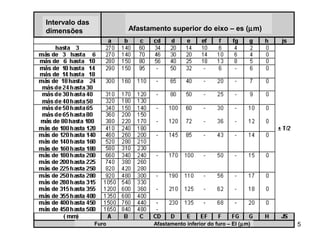
A afastamento inferior (ei) de cada zona se determina na Tabela 6 e
será:

10. 10
Tabela 5 Valores da tolerância en µ m

11. 11
Intervalo das
dimensões
Afastamento superior do furo - ES (µm)
(graus de tolerâncias maiores que 7)
Afastamento inferior do eixo + ei (µm)
Furo

12. 12
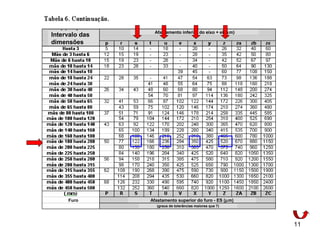
Para s7 ei = 122 µm, para u8 ei = 236 µm, para x8 ei = 350 µm
e para z8  ei = 520 µm.
Seleciona-se a zona u8.
Comprovando
Amin
= ei – ES ≥ Anec
 Amin = 236 – 72 = 164 µm
A min = 164 > Anec = 61,27 µm ⇒ OK
Verificando a resistência.
Amax
= es – EI ≤ [A]
Conhece-se que: T = es - ei  es = T8 + ei
Amax = 308 < [A] = 344,44 µm ⇒ OK
Diâmetro interior do cubo: 





+
+
0
0,072
200H8φ
Diâmetro exterior do eixo:
= 72 + 236 = 308 µm

13. 13
5.- Cálculo de ∆t na montagem com variação de temperatura.
dα3
10
JnecAmax
t
+
=∆
8
H8
para
f
JmedJnec =
2
maxmin JJ
Jmed
+
=
f8 es = – 50µm (Tabela 6) ei= es – T8 = – 50 – 72 = – 122µm
m50)50(0min µ=−−=−= esEIJ m194)122(72max µ=−−=−= eiESJ
α = 12 (10)-6
1/°C
Se a temperatura do meio exterior to é de 40o
C  t2
= t0
+ ∆ t = 40 + 179,16 = 219,16 o
C

14. 14
Intervalo das
dimensões
Afastamento superior do eixo - es (µm)
Furo Afastamento inferior do furo +EI

15. 15
Tabela 5 Valores da tolerância en µm

16. 16
Intervalo das
dimensões
Afastamento superior do eixo - es (µm)
Furo Afastamento inferior do furo +EI

17. 17
Tabela 5 Valores da tolerância en µ m

18. 18
Cálculo das uniões com chavetas.

19. 19
Dimensões
padronizadas
Medida nominal
da chaveta
Diâmetro da
árvore
Medida nominal do rasgos
Chamfro S Raio rProfundidade
Arvore Cubo
Tabela Dimensões das chavetas prismáticas padronizadas
Onde:
b e h: largo e altura da seção transversal
t1 e t2: profundidades dos rasgos.
l: comprimento da chavêta

20. 20
2- Determine as dimensões da chaveta necessária para a união eixo cubo
mostrada na figura e verifique a resistência se o material da mesma é aço de baixo
conteúdo de carbono com tensão de escoamento de 220 MPa e se requer um fator
de segurança de 2. Deve-se transmitir um momento de torção de 800 Nm.
Busca-se na tabela 1 as dimensões da seção transversal da chaveta.
b x h = 22 x 14 mm
Solução

21. 21
Assume-se o cumprimento da chaveta (L) e se verifica a resistência.
Assumido L = 50 mm
e se verifica a resistência.

22. 22
Falha de união por esmagamento de rasgos ou chavêta
folgas
braço
esmagamento
Falha da chavêta por corte
carga sobre a
chavêta
braço
Cargas que atuam

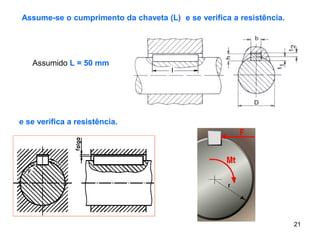
23. 23
[ ]CC
hd
T4
σ≤=σ

T = 800 000 Nmm
MPaC 14,57
508014
)000800(4
=
⋅⋅
=σ
[σ]c
= σy
= 220 MPa
57,14 MPa < 220 MPa
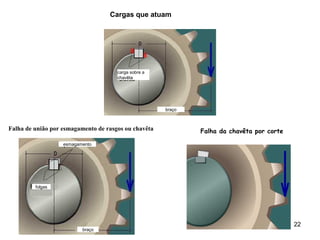
RESISTE AO ESMAGAMENTO
Verificação da resistência ao corte.
[ ]τ≤=τ
bd
T2
MPa18,18
508022
)000800(2
=
⋅⋅
=τ
[ ] [ ] MPaY
Y
66)220(3,03,0
2
6,06,0 ===== σ
σ
στ
18,18 MPa < 66 MPa
RESISTE AO CORTE
Verificação da resistência ao
esmagamento.

24. 24
Medida nominal
da chaveta
Diâmetro da
árvore
Medida nominal do rasgos
Chamfro S Raio rProfundidade
Arvore Cubo
Tabela Dimensões das chavetas prismáticas padronizadas