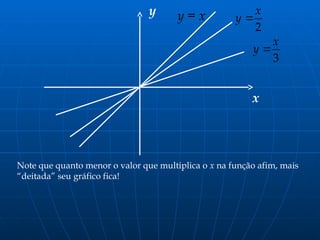
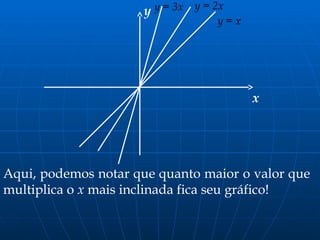
O documento discute a função afim, exemplificando como calcular o valor a ser pago por pães e comparando propostas de empresas de telefonia. A relação entre variáveis é apresentada como y = a·x + b, com a sendo o coeficiente angular e b o coeficiente linear. Além disso, o texto aborda a formação do gráfico da função afim e a inclinação da reta associada ao valor de a.

1. FUNÇÃO AFIM
Profª. Kaline Souza
Kaline.santos@ifrn.edu.br

2. Considere uma padaria que venda pãozinho por
unidade, cujo valor é R$ 0,15.
Assim, se for informada a quantidade de pães a ser
comprada, podemos dizer qual o valor a ser gasto.
Considere a tabelinha a seguir, sendo x o número de
pães e y o valor a ser pago pelos pães comprados
x y
1 0,15
2 0,30
3 0,45
4 0,60
Percebemos claramente que para
determinar o valor a ser pago (y) basta
multiplicar o número de pães (x) por 0,15
Podemos assim exibir a relação entre as
variáveis x e y da seguinte forma:
y = 0,15· x

3. Vejamos outro exemplo.
Agora suponha que você recebeu duas propostas de
empresas telefônicas para a obtenção de uma linha de celular.
A empresa “Iluminado” propõe R$ 35,00 como valor fixo
da assinatura mensal e R$ 0,15 o valor de cada minuto.
Já a empresa “Olá” propõe R$ 20,00 o valor fixo da
assinatura mensal e R$ 0,25 por cada minuto utilizado.
Considerando as duas propostas apresentadas, a partir de
quantos minutos usados em um mês é mais vantajoso usar a
operadora “Iluminado”?

4. Solução do Exemplo:
Vejamos que tanto na empresa “Iluminado” quanto na empresa
“Olá” temos um valor fixo e outro variável.
Para determinar o total (y) a ser pago na conta da empresa
“Iluminado” basta multiplicarmos o número de minutos (x)
gastos por R$ 0,15 e somarmos a esse resultado o valor da
assinatura que é R$ 35,00 gerando a relação:
y = 0,15· x + 35
O mesmo processo é usado para a empresa “Olá” onde
obtemos a relação:
y = 0,25· x + 20
Para obtermos o mesmo valor nas duas empresas basta
fazermos:
0,15· x + 35 = 0,25· x + 20

5. 0,15· x + 35 = 0,25· x + 20
0,15· x – 0,25· x = 20 – 35
– 0,10· x = – 15 · (– 1)
0,10· x = 15
x = 15/0,10
x = 150 minutos
Portanto, após 150 minutos é mais vantajoso usar a empresa
“Iluminado”.

6. Nos dois exemplos anteriores vimos situações práticas
que descrevem uma relação de dependência entre as variáveis x
e y.
Essa relação é chamada de Função Afim, ou de Função
Polinomial do 1º grau.
É toda função f : IR  IR, definida por:
y = a· x + b,
onde a e b são números reais e a ≠ 0.
Os números a e b são denominados, respectivamente,
de coeficiente angular e coeficiente linear.

7. Formação do gráfico da função Afim
Para determinar o gráfico de uma função afim basta que tenhamos dois
pontos no plano, isto é, dois pares ordenados pertencentes à função.
Assim, basta fazermos uma tabelinha com dois pontos como a seguir:
x y
Considere a função y = 3x + 3
y = 3x + 3
1
y = 3· 1 + 3
y = 3 + 3
y = 6
y = 3· 0 + 3
y = 0 + 3
y = 3
6
0 3 1
0
3
6
x
y

8. Formação do gráfico da função Afim
Vejamos outro exemplo: y = – x + 4
Façamos novamente uma tabelinha com dois pares ordenados
x y
y = – x + 4
1 3
3 1
x
y
1 3
1
3
4
y = –1 + 4
y = 3
y = –3 + 4
y = 1

9. Podemos perceber nos dois gráficos anteriores que:
a > 0  reta crescente
a < 0  reta decrescente
+
– x
x
+
–
raiz
raiz

10. x
y y = x
2
x
y 
3
x
y 
Note que quanto menor o valor que multiplica o x na função afim, mais
“deitada” seu gráfico fica!

11. y = x
y = 2x
y = 3x
x
y
Aqui, podemos notar que quanto maior o valor que
multiplica o x mais inclinada fica seu gráfico!

12. O Baião da Função Afim...
Eu vou mostrar pra vocês como se estuda função.
Se vocês querem aprender, favor prestar atenção!
Na função do 1º grau o gráfico é uma reta!
f(x) = ax + b é o que interessa.
A função do 1º grau é crescente ou decrescente!
E o sinal de a é quem indica isso pra gente.
Profª. Kaline