Este documento fornece instruções passo-a-passo sobre como separar páginas numeradas e não numeradas no Microsoft Word. Explica como usar quebras de seção para dividir o documento em diferentes seções e como desvincular a numeração de páginas entre seções para que apenas algumas seções sejam numeradas.

1. UNIVERSIDADE AGOSTINHO NETO
FACULDADE DE ENGENHARIA
DEPARTAMENTO DE ELECTRONICA E ELECTROTECNIA
DEE
Como separar páginas numeradas e não numeradas no Word
Posted on March 15, 2011
Separando páginas numeradas e não numeradas no Word 2007
Prof. Walter Moreira – Unesp/FFC/DCI – walter.moreira@marilia.unesp.br
Para que a numeração apareça apenas na parte textual do TCC (ou seja, a partir da Introdução) é
preciso usar um recurso chamado “Quebra de seção”. Este recurso possibilita a divisão do
documento em partes (seções), como se existisse mais de um arquivo dentro do mesmo documento.
Passo-a-passo
1. Abra o documento e clique no final da última linha que contém o Sumário.
2. Na aba Início, clique em Mostrar tudo, localizado no canto superior direito do bloco Parágrafo
(Figura 1)
Figura 1 – Mostrar tudo
3. Na aba Layout da Página, clique em Quebras e, dentro de Quebra de Seção, clique em Próxima
Página (Figura 2).

2. Figura 2 – Quebras

3. 4. Após este processo, o final de sua página deve ficar como na Figura 3.
Figura 3 – Quebra de seção (próxima página)
5. Dê um clique duplo no cabeçalho da página seguinte à que contém a Quebra de Seção, no nosso
caso, a página de Introdução. Observe as informações Cabeçalho-Seção2-, à esquerda, e Mesmo
que seção anterior, à direita. Observe também que aparece acionada aba Design, com a função
Vincular ao Anterior ativada (Figura 4).
Figura 4 – Cabeçalho de seção
6. O “segredo” está exatamente nesta opção. Em nosso caso queremos cabeçalhos diferentes nas
duas seções, isto é, queremos número de página apenas na seção 2 (desvinculada da seção 1), por
isso é preciso desabilitar a função Vincular ao Anterior.
7. Agora podemos inserir o número de página. Para isso clique na aba Inserir, selecione a opção
Número de página, depois em Início da página e, se preferir, Números sem formatação (Figura 5).

4. Figura 5 – Inserir número de página
Pronto!
This entry was posted in outros and tagged paginação, sumário, tcc, word by Walter. Bookmark the
permalink.
31 thoughts on “Como separar páginas numeradas e não numeradas no Word”
1. Priscila on March 16, 2011 at 7:35 pm said:
Muito bom, professor. No ano passado penei até descobrir que era assim. Queria aprender.
Reply ↓
2. Maria Aparecida Lemos de Souza on May 25, 2011 at 1:32 pm said:
Boa tarde prof.º Walter, obrigada pela dica.
Por favor continue nos dando dicas úteis como esta.
Cida Bibliotecária FATEA
Reply ↓

5. 3. Maria Aparecida Lemos de Souza on May 25, 2011 at 1:33 pm said:
Obrigada prof.º pela dica. Continue a nos passar estas dicas tão úteis.
Cida
Reply ↓
o Walter on May 25, 2011 at 8:59 pm said:
Oi, Cida,
boa vontade (aquela mesma que já encheu outro lugar), eu tenho, tempo… tempo….
tempo… tempo…. este “senhor tão bonito quanto a cara do meu filho” (Velô) ….
anda raro.
Reply ↓
4. Dani on July 15, 2011 at 4:16 pm said:
“Velô” foi ótima.
Vc poderia deixar o site que vc passou pro meu word ancião, para os que também não estão
tão atualizados né mesmo?!
uauahuaha
Reply ↓
5. Loriane on June 18, 2012 at 2:01 pm said:
O meu worrd 2007 não tem esta opção vincular com anterior habilitado!
Reply ↓
o Walter on June 20, 2012 at 8:59 am said:
Neste caso, fica mais simples ainda, pois isso já vai criar cabeçalhos diferentes para
as duas seções.
Reply ↓

6.  Thais on January 14, 2013 at 9:23 am said:
No meu computador a opção também não está habilitada mas não consigo
fazer esta alteração, porque quando eu mudo um, muda todos
Reply ↓
6. Leoni Cordeiro on November 28, 2012 at 8:25 pm said:
Walter…preciosas dicas! Muito obrigada por compartilhar seu conhecimento!! Abraços
Reply ↓
o Walter on November 29, 2012 at 4:49 pm said:
Obrigado, Leoni. Que bom que lhe foi útil.
[]s,
Reply ↓
7. jonas almada on January 26, 2013 at 10:03 am said:
Prefeita a dica, nunca escrevo nos comentários mas este aqui não poderia deixar de
agradeçer pela ajuda preciosa.
Reply ↓
o Walter on January 28, 2013 at 7:27 am said:
Obrigado, Jonas.
Reply ↓
8. ROSIANE on March 2, 2013 at 9:17 am said:

7. Obrigada professor,muito boa sua explicação,simples porém de grande ajuda.
Abraços.
Reply ↓
o Walter on March 5, 2013 at 9:58 am said:
Que bom que lhe ajudou. Abraço.
Reply ↓
9. Maria Bethânia on April 25, 2013 at 3:24 pm said:
Nossa!!!!!!!!!!!! Tudo que eu precisava!!!
Obrigada por ser sucinto e eficiente.
Valeu.
Reply ↓
10. Dani on May 24, 2013 at 2:57 pm said:
Não consigo encontrar a opção vincular com anterior no meu word 2007,pois depois que
faço a parte de quebra de seção quando eu vou colocar a numeração fica errado do meu
jeito,começa a numerar na primeira pag…por favor me ajude ^^
Reply ↓
o Walter on May 27, 2013 at 9:02 am said:
Dani, veja isso: http://www.infowester.com/tutpagword.php . Acho que vai lhe
ajudar.
[]s,
Reply ↓
11. fabiana silva lopes on September 29, 2013 at 4:28 pm said:

8. Alguém pra me ajudar como faço pra quebrar pagina, como a regra da OAB.
Reply ↓
12. Kesia on January 24, 2014 at 4:12 pm said:
Nossa, muito obrigada! Eu sempre fazia meus trabalhos em dois documentos por não
conseguir arrumar as páginas. Agora consegui! Obrigada!
Reply ↓
13. ADRIANE SOUZA on February 11, 2014 at 10:28 pm said:
MEU WORD NÃO APARECE VINCULAR AO ANTERIOR, ESTA INDISPONÍVEL
TEM COMO FAZER DE OUTRA FORMA?
Reply ↓
o Luana on March 6, 2014 at 12:26 am said:
Oi Adriane,
Eu estava com o mesmo problema e descobri, graças ao tutorial do professor Walter,
que existe uma diferença entre inserir a quebra pelo menu Inserir e pelo menu
Layout da Página (neste a opção de Quebras está dentro da opção Configurar Página
– o ícone é pequeno). Eu tentei inúmeras vezes pelo menu Inserir e não obtive êxito.
Quando tentei pelo menu Layout da Página, consegui na primeira tentativa. Acredito
que consegui porque pude escolher a opção da Quebras de Seção-Próxima Página. É
importante ser a opção Próxima Página. Daí é só seguir o que o professor
apresentou!
Espero ter ajudado!
Reply ↓
14. Estela Solfa on March 19, 2014 at 4:35 pm said:
Prof. Excelente material, muito obrigada.
Reply ↓

9. 15. Carlos Vinicius on October 31, 2014 at 2:57 pm said:
O mulher tutorial de paginação encontrado na net. Valeu, bom trabalho, ajudou bastante.
Reply ↓
o Walter on November 1, 2014 at 10:36 am said:
Que bom, Carlos Vinicius, que lhe foi útil! Obrigado.
Reply ↓
16. Bernardino Coelho da Silva on November 9, 2014 at 7:04 am said:
Melhor e mais simples explicação sobre o tema que encontrei. Grato!
Reply ↓
17. Luisa on November 23, 2014 at 11:40 am said:
Professor,
Consegui desvincular e tudo mais. Entretando, quando coloco a numeração na página, fica a
mesma numeração pra todas as páginas. O que estou fazendo de errado?
Reply ↓
o Walter on November 24, 2014 at 9:30 am said:
Luisa, provavelmente, se a numeração está sequencial, significa que não foram
criadas duas seções para o documento. Dê uma pesquisada sobre como criar seções
no documento word, acho que vai lhe ajudar.
[],
Reply ↓

10. 18. Hellan Rodrigues da Silva on December 17, 2014 at 8:58 am said:
Ótimo post, já estava desesperado procurando por algum artigo que me ajudasse com a
paginação. Valeu mesmo
Reply ↓
19. Jonathan on February 17, 2015 at 2:23 pm said:
Caro professor,
Tua postagem foi extremamente útil, mas estou com o seguinte problema: tenho de incluir a
numeração das páginas em um arquivo que contém cinco seções diferentes, e o Word só
começa a numerar a partir da quinta seção, como página 1. Eu quero justamente incluir a
paginação a partir da seção 2, mas não consigo, pois a partir da seção 5 permanece a mesma
numeração anterior. Já tentei (dezenas de vezes) vincular uma seção à outra, mas isso não
muda nada. Podes me informar, por favor, como posso criar um texto com apenas duas
seções, extinguindo as outras três e mantendo a mesma paginação a partir da segunda seção?
Ressalto que estou revisando o texto para outra pessoa, que foi quem criou essas inúmeras
seções. Muito obrigado!
Reply ↓
o Walter on February 28, 2015 at 4:44 pm said:
Jonathan, em cada versão do Word resolvem complicar ainda mais algumas coisas
que são muito simples, por isso essas ferramentas nos dão tanta dor de cabeça. Sobre
a exclusão de seções, veja https://support.office.com/pt-br/article/Excluir-uma-
quebra-de-seção-1e12f200-7215-4688-a55a-5130f383dc5f?ui=pt-BR&rs=pt-
BR&ad=BR.
[],
Reply ↓
20. Frei FErnâncio on February 22, 2015 at 4:39 pm said:
ok, tudo certo, valeu e bons ensinamentos para o povo!
Reply ↓

11. Leave a Reply
Your email address will not be published. Required fields are marked *
Name *
Email *
Website
Comment
Proudly powered by WordPress
ANÁLISE DOS PROCESSOS DE ARRANQUE E PARAGEM DOS MOTORES
DE INDUÇÃO TRIFÁSICOS
Alunos: Schields Abel Gaspar Pedro
& Wellington Nkuto Nanga
Orientador: Dr. Eng. Angel Costa Montiel
Co-Orientador: Msc. Eng. Joaquim Moreira Lima

12. LUANDA
2012

13. Schields Abel Gaspar Pedro
&
Wellington Nkuto Nanga
ANÁLISE DOS PROCESSOS DE ARRANQUE E PARAGEM DOS MOTORES
DE INDUÇÃO TRIFÁSICOS
Monografia, apresentada ao Departamento de
Electrónica e Eletrotecnia da Faculdade de
Engenharia da Universidade Agostinho Neto
(UAN), para a atenção do grau de Engenheiros
Eletrotécnico na Especialidade de “Sistema de
Potência”.
Orientador: Dr. Eng. Angel Costa Montiel
Co-Orientador: Msc. Eng. Joaquim M. Lima
LUANDA
2012

14. AGRADECIMENTO
Ao professor e orientador Dr. Eng. Angel Costa Montiel, pela confiança em nós e em nosso
trabalho.
Aos demais professores do curso, que proporcionaram a nós uma gama de conhecimentos,
úteis para o desenvolvimento desse trabalho.
A todos os colegas pela disponibilidade e paciência.
Aos nossos pais e familiares, pelo apoio dado durante todo o curso, principalmente nos
momentos mais difíceis.
A Deus, principalmente.
i

15. “Entrega o teu caminho ao Senhor; confia nele, e ele tudo fará.”
Salmos 37:5
ii

16. ÍNDECE
Como separar páginas numeradas e não numeradas no Word........................................................................3
31 thoughts on “Como separar páginas numeradas e não numeradas no Word” .......................................6
Leave a Reply .........................................................................................................................................13
Alunos: Schields Abel Gaspar Pedro..........................................................................................................13
AGRADECIMENTO..............................................................................................................................................i
ÍNDECE.............................................................................................................................................................iii
LISTA DE FIGURAS.............................................................................................................................................v
LISTA DE TABELA.............................................................................................................................................vii
RESUMO.........................................................................................................................................................viii
ABSTRACT........................................................................................................................................................ix
INTRODUÇÃO...................................................................................................................................................1
CAPÍTULO I .......................................................................................................................................................2
MOTOR ASSINCRONO DE INDUÇÃO ................................................................................................................2
Ao ser alimentado por uma rede de tensão e frequência constantes sua velocidade varia pouco perante
variações na carga mecânica............................................................................................................................5
CAPÍTULO II ....................................................................................................................................................13
ARRANQUE E PARAGEM DE MOTORES ASSINCRONOS..................................................................................13
CAPÍTULO III ...................................................................................................................................................30
MODELO MATEMATICO DO MOTOR ASSÍNCRONO .......................................................................................30
CAPÍTULO IV ..................................................................................................................................................56
ANÁLISE DE UM ESTUDO DE CASO.................................................................................................................56
CONCLUSÕES..................................................................................................................................................78
RECOMENDAÇÃO...........................................................................................................................................79
.......................................................................................................................................................................79
BIBLIOGRAFIA.................................................................................................................................................79
Apêndece.......................................................................................................................................................80
iii

17. LISTA DE FIGURAS
Figura 1.1: a) Corte Transversal do Motor de Indução Trifásico; b) Esquema do Circuito com
Resistências Externas; c) Esquema de Circuito do Motor sem Resistências Externas........................2
Figura 1.2: Componentes de uma Máquina Assincróna de Gaiola de Esquilo...................................6
Figura 1.3: Circuito Equivalente por Fase do Motor Assíncrono Trifasico em Repouso...................7
Figura 1.4: Circuito Equivalente por Fase do Rotor...........................................................................7
Figura 1.5: Circuito Equivalente do Rotor Referido à Frequência do Estator....................................8
Figura 1.6: Circuito Equivalente Exacto do Motor Assincrono por Fase...........................................8
Figura 1.7: Circuito Equivalente Exacto do Motor Assíncrono com Separação da Potencia.............9
Figura 1.8: Circuito Equivalente tipo L do Motor Assincrono Trifásico............................................9
Figura 1.9: Característica do Binário Electromagnético e do Escorregamento do Motor Assincrono
............................................................................................................................................................11
Figura 2.1: Circuito equivalente em Assincrono Motor de Arranque...............................................15
Figura 2.2: Diagramas Fasoriais do Motor para Diferentes Resistências do Rotor..........................15
Figura 2.3: Esquema do Circuito de Arranque do Motor de Rotor Bobinado..................................16
Figura 2.4: Variação das Características Mecânicas do Esquema da figura 12................................17
Figura 2.5: Barras do rotor no Motor Assíncrono de Gaiola de Esquilo..........................................18
Figura 2.6: Esquema do Arranque por Auto Transformador............................................................19
Figura 2.7: Arranque Estrela-Triângulo............................................................................................20
Figura 2.8: Regulador de Tensão Estático Utilizado nos Soft Starters.............................................21
Figura 2.9: Comparação das Correntes no Arranque com Diferentes Métodos...............................21
Figura 2.10: Variação da Tensão Aplicada no Soft Starter Programado com Rampas de Aceleração
e Desaceleração..................................................................................................................................22
Figura 2.11: Variação da Corrente com Ajuste de Limitação de Corrente Fixa...............................22
Figura 2.12: Vista Externa de um Arrancador Suave com Seus Ajustes..........................................23
Figura 2.13: A Variação da Frequência Inicial e Começar Rampa S...............................................23
Figura 2.14: Esquema do Conversor Back to Back...........................................................................26
Figura 2.15: Características Mecânicas do Motor Assíncrono com paragem Regenerativa............27
Figura 2.16: Esquema de Paragem Dinâmica de um Motor Assíncrono..........................................27
Figura 2.17: Esquema de Paragem Dinâmica com o Motor Alimentado por um Conversor Estático.
............................................................................................................................................................28
Figura 2.18: Paragem por Aplicação de Corrente Contínua com o Motor Alimentado por
Conversor Estático.............................................................................................................................28
Figura 2.19: Esquema de paragem por Inverso.................................................................................29
Figura 3.1: Corte Transversal Esquemático do Motor Assíncrono...................................................30
Figura 3.2: Vector Espacial Trifásico...............................................................................................34
Figura 3.3: Vector Espacial Trifásico em Sistemas de Coordenadas Diferentes..............................36
Figura 3.4: Diagrama Fasorial Aproximado ao Circuito Equivalente..............................................45
Figura 3.5: Circuito Equivalente do Motor no Arranque..................................................................49
Figura 3.6: Circuito Equivalente do Motor no Assíncrono...............................................................51
Figura 3.7: Diagrama de fase que corresponde a equação 78...........................................................52
Figura 4.1: Sistema Hidráulico Estudado.........................................................................................63
Figura 4.2: Característica Da Instalação Hidráulica.........................................................................63
Figura 4.3: Características das Bombas LHK da Alfa Laval............................................................64
Figura 4.4: Característica da Carga Mecânica..................................................................................66
Figura 4.5: Modelo Geral em SIMULINK para o Estudo dos Procesos de Arranque e Paragem....67
Figura 4.6: Modelo da Máquina Assíncrona.....................................................................................68
Figura 4.7: Modelo da Carga Mecânica............................................................................................68
v

18. Figura 4.8: Selector de Alimentação.................................................................................................69
Figura 4.9: Bloco de Medições.........................................................................................................70
Figura 4.10: Velocidade em Função do Tempo no Arranque Directo à Rede.................................71
Figura 4.11: Corrente em Função do Tempo no Arranque Directo à Rede......................................71
Figura 4.12: Binário em Função do Tempo no Arranque Directo à Rede........................................72
Figura 4.13: Característica Mecênica Dinâmica no Arranque Directo à Rede................................72
Figura 4.14: Velocidade em Função do Tempo no Arranque a Tensão Reduzida..........................73
Figura 4.15: Corrente em Função do Tempo no Arranque a Tensão Reduzida................................73
Figura 4.16: Binário em Função do Tempo no Arranque a Tensão reduzida...................................73
Figura 4.17: Característica Mecânica dinâmica no Arranque a Tensão Reduzida...........................74
Figura 4.18: Velocidade em Função do Tempo no Arranque Suave na Rampa...............................74
Figura 4.19: Corrente em Função do Tempo no Arranque Suave na Rampa..................................74
Figura 4.20: Binario em Função do Tempo no Arranque Suave na Rampa.....................................75
Figura 4.21: Característica Mecânica Dinámica no Arranque Suave na Rampa..............................75
Figura 4.22: Velocidade em Função do Tempo no Arranque Suave Em S......................................75
Figura 4.23: Corrente em Função do Tempo no Arranque Suave em S...........................................76
Figura 4.24: Binário em Função do Tempo no Arranque Suave em S.............................................76
Figura 4.25: Característica Mecânica Dinâmica no Arranque Suave em S.....................................76
Figura 4.26: Velocidade em Função do Tempo no Arranque a Frequência Variavel na Rampa....77
Figura 4.27: Corrente em Função do Tempo no Arranque a Frequência Variavel na Rampa.........77
Figura 4.28: Binário em Função do Tempo no Arranque a Frequência Variavel na Rampa............77
Figura 4.29: Característica Mecânica Dinâmica no Arranque a Frequência Variavel na Rampa...78
Figura 4.30: Velocidade em Função do Tempo no Arranque a Frequência Variavel em S.............78
Figura 4.31: Corrente em Função do Tempo no Arranque a Frequência Variavel em S..................78
Figura 4.32: Binário em Função do Tempo no Arranque a Frequencia Variavel em S....................79
Figura 4.33: Característica mecânica Dinámica no Arranque a Frequência Variavel em S.............79
Figura 4.34: Variação da Velocidade na Paragem Dinâmica...........................................................81
Figura 4.35: Variação da Corrente na Paragem Dinâmica...............................................................81
Figura 4.36: Variação do Binário na Paragem Dinâmica.................................................................81
Figura 4.37: Variação da Velocidade na Paragem por Inversão......................................................82
Figura 4.38: Variação da Corrente na Paragem por Inversão...........................................................82
Figura 4.39: Variação do Binário da Paragem por Inversão............................................................82
vi

19. LISTA DE TABELA
Tabela 4.1: Dados do Catalogo do Motor.........................................................................................51
Tabela 4.2: Valores Base...................................................................................................................57
Tabela 4.3: Parâmetros do Motor Assíncrono...................................................................................57
Tabela 4.4: Pontos da Característica Mecânica param a Tabela de Look Up...................................58
Tabela 4.5: Possibilidades do Selector de Alimentação....................................................................61
Tabela 4.6: Comparação de Arranques.............................................................................................72
vii

20. RESUMO
.
Como é conhecido, o motor de indução trifásico é o consumidor de mais do 60 % da energia
eléctrica na indústria. Um dos principais problemas destes motores em sua utilização industrial é a
elevada corrente que consomem no arranque que pode provocar importantes quedas de tensão na
indústria, prejudicando a operação do resto dos motores e das demais cargas. Em alguns casos
também é necessário parar estes motores muito rapidamente.
Esta tese se propõe como objectivo fazer uma análise destes processos. Para fazê-lo é
necessário considerar um modelo do motor assíncrono trifásico que tenha em conta a variação da
resistência e a reactância do rotor no arranque e na paragem. A realização deste modelo no
SIMULINK do software MATLAB permitirá conhecer os valores de corrente no arranque e sua
duração no tempo e um melhor ajuste das protecções.
O primeiro capítulo apresenta um resumo das características de construção e funcionamento
dos motores assíncronos trifásicos destacando a sua simplicidade, robustez e pouca necessidade de
manutenção. No segundo capítulo explicam-se os diferentes métodos de arranque e paragem desses
motores. O terceiro segue o modelo dinâmico apropriado para o estudo deste tipo de processos e
descreve um método simples para a identificação dos seus parâmetros a partir dos dados do
catálogo do motor. Finalmente, no último capítulo comparam-se os diferentes métodos de arranque
e paragem através de um modelo SIMULINK elaborado pelo orientador principal desta tese.
Baseia-se no modelo derivado no capítulo anterior.
Palavras-Chave: Motor de Indução, Arranque e Paragem, Matlab.
viii

21. ABSTRACT
As it is known, the three-phase induction motor is the consumer of more than 60% of the
electrical power in industries. One of the chief problems of these engines in its industrial use is the
high current they consume at starting that can cause significant voltage drops in industries,
impairing the operation of the other motors and the of other loads. In some cases it is also necessary
to stop these motors very quickly.
The goal of this thesis is to analyze these processes. To analyze them it is necessary to
consider a three-phase asynchronous motor model that takes in consideration the variation of the
rotor resistance and reactance at starting and shutting down. The realization of this model in
MATLAB SIMULINK software will reveal the values of the current at starting and its duration in
time and a better fit of the protections.
The first chapter summarizes the features of construction and operation of the three phase
asynchronous motors highlighting its simplicity, robustness and a little necessity of maintenance. In
the second chapter it is explained the different methods of starting and stopping these engines. The
third follows the dynamic model suitable for the study of such processes and describes a simple
method for identification of its parameters from the data of the engine catalogue. Finally, the last
chapter compares the different methods of starting and stopping through a SIMULINK model
developed by the head-tutor of this thesis. It is based on the model taken from the previous chapter.
Key words: Induction Motor, Starting and Stopping, Matlab.
ix

22. INTRODUÇÃO
Como é bem conhecido, o motor assíncrono trifásico de rotor de gaiola ou de rotor em curto-
circuito é do tipo de motor mais usado na indústria e constitui a força motriz mais importante neste
tipo de instalações. A partir de vários estudos, foi identificado que mais de 60% da energia
consumida pelas indústrias é feita por intermédio dos motores trifásicos assíncronos e, dentro deste
por cento, mais de 70% movem bombas, compressores ou ventiladores cujo binário mecânico
resistente é a função da velocidade.
Há uma série de estudos focados na redução de consumo de energia dos motores assíncronos
que accionam este tipo de mecanismos principalmente mediante a utilização de motores de alto
rendimento e a utilização de variadores de velocidade quando se quer regular o caudal ou fluxo de
fluido movido por mecanismo.
Entretanto, poucos estudos se têm dedicado a analisar os processos dinâmicos de arranque e
de paragem nestes mecanismos. A sua importância é que, mediante uma selecção adequada do tipo
e do dispositivo de arranque e paragem podem evitar-se fenómenos mecânicos que produzem
desgastes adicionais neste tipo de carga mecânica.
O impressionante desenvolvimento da electrónica de potência tem permitido construir
conversores para variar e controlar a velocidade e a corrente destes motores e, assim, permitir uma
utilização mais racional do mecanismo accionado tanto do ponto de vista energético, como do ponto
de vista de aumentar a vida útil e reduzir a reparação e manutenção das bombas, ventiladores e
compressores. Os mais importantes são os conhecidos como arrancadores suaves (Soft starters) e os
variadores de velocidade (Variable Frequency Drives).
O objectivo principal desta tese é precisamente analisar e comparar os diferentes tipos de
arranque e travagem nos motores assíncronos trifásicos de um modelo dinâmico que considera
todos os parâmetros e sua simulação em SIMULINK do software MATLAB.
1

23. CAPÍTULO I
MOTOR ASSINCRONO DE INDUÇÃO
1.1. PRINCÍPIO DE FUNCIONAMENTO
No motor de indução a corrente alternada é fornecida diretamente ao estator, ao passo que o
rotor recebe a corrente por indução, como em um transformador, a partir do estator.
Quando o motor é alimentado por uma fonte trifásica equilibrada, um campo magnético é
produzido no entreferro girando na velocidade síncrona. Esta velocidade síncrona depende do
número de polos do estator e da frequência imposta no estator do motor de indução.
A figura 1.1 mostra o diagrama e o circuito eléctrico de ligação de uma máquina assíncrona ou de
indução trifásica. No enrolamento do estator, existe um enrolamento trifásico (fase A-A', B-B' e C-C'), na
qual se produz um campo magnético giratório cuja velocidade (ωs) depende do número de polos (P) e da
frequência (f1) da rede de eletricidade que o alimenta:
)2/(
..2 1
P
f
s
π
ω = (1.1)
Figura 1.1: a) Corte Transversal do Motor de Indução Trifásico; b) Esquema do Circuito com Resistências Externas;
c) Esquema de Circuito do Motor sem Resistências Externas.
Quanto aos aspectos construtivos do rotor de um motor de indução, tem-se:
2

24.  Motores com rotor bobinado;
 Motores com rotor gaiola de esquilo.
O rotor bobinado tem um enrolamento trifásico de mesmo número de polos e fase que o do
estator e cujos terminais estão ligados a três anéis deslizantes sobre os quais repousam três escovas
através das quais podem introduzir-se resistências externas (como se mostra na figura 1.1 b) ou
ligar-se a outro circuito externo. Por outro lado, rotor de gaiola compreende um certo número de
barras, de cobre ou de alumínio, curto circuitados através de anéis situados nas extremidades do
rotor. Como pode ver-se, o rotor bobinado permite modificar as características de comportamento
do rotor e o de gaiola não. A simplicidade e a robustez na construção do rotor em gaiola
representam vantagens notáveis para esse tipo de motor de indução e fazem dele o tipo de motor
mais comumente utilizado na indústria. Embora o rotor seja de gaiola para estudo pode se supor um
rotor equivalente, com os seus terminais curto circuitados (como se mostra na figura 1.1c).
Para analisar o princípio de funcionamento desta máquina (neste caso, deverá funcionar
como um motor), se supõem primeiro que o circuito do rotor está aberto e que, portanto, apena
circula corrente através do enrolamento do estator. Este corrente serve para produzir o campo
magnético de acoplamento (desprezando as perdas do núcleo) e é denominado Corrente de
Magnetização, ou seja, para cada fase se cumpre que:
Ms ii = (1.2)
Onde:
iM – Valor instantâneo da corrente de magnetização;
Esta corrente provoca uma força magnetomotriz giratória mF

e um fluxo φm que induz uma
força electromotriz no estator igual a:
mdevsSS KNfE φπ .....2= (1.3)
Onde:
Ns – Número de espiras por fase do enrolamento do estator;
KdevS – Factor de enrolamento do estator que leva em conta a distribuição das bobinas
pelo estator e o possível encurtamento do passo;
Também em cada fase do rotor se induz uma fem ER dada por:
mdevsRR KNfE φπ .....2= (1.4)
Neste caso o rotor não gira devido à corrente que não circula por ele.
Se agora se fecha o circuito do rotor começa a circular corrente por ele. Esta corrente
relaciona com o fluxo giratório do entreferro (φm ) e cria um binário electromagnético que faz rodar
3

25. o motor, acelerando-o. Esta rotação ocorre no mesmo sentido que a do fluxo giratório, trazendo
como consequência que a velocidade relativa dos condutores do rotor, com respeito ao fluxo do
estator, diminua, diminuindo, por tanto, a fem induzida no rotor e a corrente. Este processo de
redução de corrente e aumento da velocidade continua até que o valor de corrente é tal, que o
binário que se produz equilibra o binário externo da carga mecânica do motor. Então, a velocidade e
o valor eficaz da corrente são constantes e se atinge o estado estacionário. Esta velocidade ωm
estáveis deve ser menor que a velocidade síncrona Sω na qual se move o fluxo giratório para que
exista movimento relativo entre o fluxo e os condutores do rotor. Maior carga mecânica externa
maior velocidade relativa, maior fem induzida e maior corrente, isto implica menor velocidade do
rotor. O valor da velocidade relativa em por unidade é denominado Escorregamento e é dada por:
S
mS
s
ω
ωω −
= (1.5)
Devido à queda de tensão no estator da máquina ser muito pequena, a tensão aplicada é
praticamente igual à fem induzida. Isto quer dizer que se a tensão permanece constante, a fem
induzida também o faz e o fluxo do entreferro não varia, a frequência da fem e a corrente do rotor
depende da velocidade relativa deste e do fluxo giratório do entreferro e é, portanto, igual a:
f s f2 1= . (1.6)
É importante demonstrar também que o fluxo do rotor gira com respeito ao estator à
velocidade síncrona, independentemente do valor do escorregamento e por tanto, da frequência do
rotor.
A velocidade do fluxo do rotor com respeito ao rotor ωFRR
depende da frequência da
corrente do rotor e é igual, por tanto, a:
SFRR s ωω .= (1.7)
Por outra parte, a velocidade desta fmm com respeito ao estator é igual a sua velocidade
com respeito ao rotor mais a velocidade do rotor:
ω ω ωFRS FRR R= + (1.8)
Da equação 1.5 vesse que a velocidade do rotor em função do deslizamento é igual a:
)1.( sSR −=ωω (1.9)
Substituindo a equação 1.7 e 1.9 na equação 1.8:
SSSFRS ss ωωωω =−+= )1.(. (1.10)
Assim demonstrou-se o que queríamos provar. Esta propriedade faz com que o binário
electromagnético do motor permanece sempre constante pois é produzido pela interacção entre os
fluxos que rodam à mesma velocidade, ou seja, são fixos em relação um ao outro.
4

26. É importante notar, finalmente, alguns princípios básicos para a construção e operação da
máquina assíncrona ou de indução trifásica, que caracterizam e diferenciam das demais:
 Ao ser alimentado por uma rede de tensão e frequência constantes sua velocidade
varia pouco perante variações na carga mecânica.
 Para que funcione como gerador deve acoplar-se um motor primário, conectar-lhe à rede
e fazer-lhe rodar a uma velocidade superior à síncrona.
 O campo magnético de acoplamento, necessária para produzir a conversão de energia
eletromecânica, surge a partir da tensão trifásica de alimentação do estator, o que
significa que este campo não pode ser controlado, se a máquina é alimentada por uma
rede de tensão e frequência constante. Isso resulta em vários factos importantes:
primeiro, não pode funcionar como um gerador, se não for ligado em paralelo com um
ou mais geradores síncronos, a rede eléctrica ou um banco de capacitores, em segundo, o
factor de potência não pode ser controlado, diminuindo ostensivamente a carga e em
terceiro lugar, existe um forte acoplamento entre os campos do estator e do rotor (ao
contrário do motor de corrente contínua) que impede a sua utilização como componente
de um sistema de controlo.
 Em todas as máquinas eléctricas é a más simples, barata, robusta e menos necessidade de
manutenção.
Na figura 1.2 pode ser visto um motor assíncrono com as peças com o nome de cada uma.
Se comparado com uma máquina DC é visto como componentes muito mais simples e sem desgaste
rápido, como escovas, anéis deslizantes (excepto o motor rotor bobinado), colector, etc. Por esse
motivo, o funcionamento como motor domina amplamente o mercado.
5

27. Figura 1.2: Componentes de uma Máquina Assíncrona Gaiola de Esquilo
1.2. CIRCUITO EQUIVALENTE DO MOTOR ASSÍNCRONO TRIFÁSICO
Para deduzir o circuito equivalente da máquina assíncrona se parte da sua semelhança com o
transformador trifásico. Uma máquina assíncrona em repouso (velocidade zero) tem a mesma
configuração electromagnético de um transformador trifásico com uma importante diferença, o
circuito magnético do transformador só apresenta material ferromagnético enquanto que no circuito
magnético da máquina assíncrona existe um entreferro entre o estator e o rotor, ou seja, um espaço
de ar entre ambos. O ar, como se sabe tem uma permeabilidade magnética muito baixa em
comparação com o aço e outro material ferromagnético e isto faz que, embora o espaço de ar seja
muito pequeno (da ordem de alguns milímetros), a sua presença aumenta notavelmente a relutância
do circuito magnético. Isto traz duas consequências práticas:
Um aumento de corrente de magnetização e de vazio, que já não pode ser desprezada como
sucede com o transformador.
Também há um aumento da reactância de dispersão, tanto do estator como do rotor.
Tendo em conta estas causas, o circuito equivalente do motor assíncrono trifásico por fase, em
condições de repouso, como se mostra na figura 1.3 sem poder desprezar, a corrente de vazio, como
foi feito com o transformador.
Neste circuito V1 é a tensão de fase e os outros parâmetros têm o mesmo significado que no
transformador.
Figura 1.3: Circuito Equivalente por Fase do Motor Assíncrono Trifásico em Repouso
Supõem-se agora que o motor começa a rodar e alcança uma velocidade tal que seu
escorregamento é s. A máquina comporta-se agora como um transformador com o secundário
rotativo. Esta velocidade relactiva do secundário (rotor) com respeito ao primário (estator) tem uma
importante consequência que é: A frequência do rotor não é igual à do estator e está dada pela
equação 1.6. Portanto deve se analisar primeiro o circuito do rotor por fase e depois referi-lo à
frequência do estator. Este circuito por fase se mostra na figura 1.4 em que E2 é a fem induzida no
rotor em repouso referida ao estator e Xd2 é a reatância de dispersão do rotor em repouso (também
6

28. referida ao estator), ou seja, à frequência da rede. Ao existir um escorregamento, ambas são
multiplicadas por este valor, a fem por um problema de velocidades relativas e a reactância por ser
proporcional à frequência que por ela circula.
Figura 1.4: Circuito Equivalente por Fase do Rotor
Mediante a equação 1.10 se demonstrou que o fluxo do rotor gira com respeito ao estator à
mesma velocidade que o fluxo do estator, ou seja, à velocidade síncrona. Isto quer dizer que as
quantidades de rotor “são vistas” desde o estator como se tivessem a mesma frequência da rede.
Isto permite referir também o rotor à frequência do estator. Para fazê-lo, deve alimentar-se o
escorregamento (s) da fem e da reactância. Isto deve fazer-se mantendo o valor da corrente do rotor
referido ao estator. Portanto:
2'
2
2
'
2
2
2'
2
2'
2
2'
2
).(
.
d
d
X
s
R
E
XsR
Es
I
+





=
+
=
(1.11)
Esta equação permite colocar o circuito equivalente do rotor como se mostra na figura 1.5 e
incorporá-lo o Circuito Equivalente Exato do Motor Assíncrona Trifásico por Fase.
Figura 1.5: Circuito Equivalente do Rotor Referido à Frequência do Estator
7

29. Figura 1.6: Circuito Equivalente Exato do Motor Assíncrono por Fase
Tendo em conta considerações energéticas, é evidente que a potência que se dissipa na
resistência R2
’
/s é a potência total que passa do estator ao rotor, denominado também Potência
Electromagnética Pem, ou seja:
s
R
IPem
'
22'
2 ..3= (1.12)
No entanto, da potência que passa do estator ao rotor, uma parte se perde na resistência do
rotor em forma de perdas de cobre do rotor ∆pcobr iguais a 3.I2
’2
.R2
’
. O resto, que geralmente é a
maior parte, é a parte da potência convertida à forma mecânica Pmec:





 −
=−=∆−=
s
s
RIRI
s
R
IpPP cobremmec
1
...3..3..3 '
2
2'
2
'
2
2'
2
'
22'
2
(1.13)
É conveniente no circuito equivalente separar a resistência onde ocorre as perdas de cobre
do rotor e a resistência cuja potência dissipada é igual à potência convertida à forma mecânica,
como mostra-se na figura 1.7. Este é outra forma de representar o Circuito Equivalente Exato do
Motor Assíncrono.
Figura 1.7: Circuito Equivalente Exato do Motor Assíncrono com Separação da Potência
Convertida à Forma Mecânica.
8

30. Este circuito equivalente exato é, como pode ser visto, do tipo T, que é relativamente de
difícil solução. Para simplificar se faz uso de um Circuito Equivalente Aproximado tipo L como se
mostra na figura 1.8. Como a corrente de vazio Io é menor que a de carga e está quase em
quadratura com a tensão (Rm é muito maior que Xm), não se comete grande erro se passar este
circuito paralelo à entrada.
Figura 1.8: Circuito Equivalente tipo L do Motor Assíncrono Trifásico
1.3. CARACTERÍSTICA MECÂNICA E CONDIÇÕES DE OPERAÇÃO DA MÁQUINA
ASSINCRONA TRIFÁSICA
Tal como já foi explicado no caso do motor de corrente contínua, a característica mais
importante de um motor eléctrico como conversor de energia electromecânica é a velocidade de
rotação em função do binário electromagnético. No caso particular da máquina assíncrona é
habitual, também expressar esta relação mediante a característica do binário electromagnético em
função do escorregamento. Esta secção se deduz ambas as características começando pela segunda.
A partir destas características se analisaram as diferentes condições de funcionamento da máquina.
Primeiramente determinou-se a expressão do binário electromagnético que é igual à
potência convertida à forma mecânica dividida pela velocidade de rotação:
R
mec
em
P
T
ω
= (1.14)
Substituindo a equação 1.13 e 1.9 em 1.14 se obtém:
s
RI
s
s
s
RI
T
SS
em
'
2
2'
2
'
2
2'
2
.
.
3
)1.(
1
...3
ωω
=
−





 −
=
(1.15)
9

31. Também pode dizer-se que o binário electromagnético é igual à potência electromagnética
ou potência que passa do estator ao rotor dividida pela velocidade síncrona.
S
em
em
P
T
ω
= (1.16)
Utilizando o circuito equivalente aproximado tipo L da figura 1.8, se deduz que a corrente
do rotor referida ao estator é igual a:
( )2'
2'
2
1
1'
2
drds XX
s
R
R
V
I
++





+
=
(1.17)
Substituindo a equação 1.17 em 1.15 se obtém uma nova expressão do binário
electromagnético:
( )








++





+
=
2'
2'
2
1
'
2
2
1
.
.
.3
drds
S
em
XX
s
R
Rs
RV
T
ω (1.18)
Esta característica tem a forma que se mostra na figura 1.9. Primeiramente deve-se destacar
que a característica define três modos de funcionamento na máquina:
Funcionamento como Motor: Ocorre quando o escorregamento é 0<s<1 e a velocidade é
0<ωR<ωS. A máquina recebe energia da rede eléctrica e a entrega à carga mecânica sendo o binário
eletromagnética do mesmo sentido que a velocidade.
Funcionamento como Gerador ou Paragem Regenerativa: Ocorre quando o
escorregamento s <0 e velocidade é ωR>ωS. A máquina recebe energia de um motor primário e
entrega a rede sendo o binário electromagnético de sentido contrario ao da velocidade.
Funcionamento em Paragem por Inversão ou Contracorrente: Ocorre quando o
escorregamento s>1 e a velocidade é ωR<0. A máquina recebe energia da parte mecânica e da rede
eléctrica simultaneamente, esta energia se dissipa no rotor da máquina. É utilizado para paragens
muito rápidas ou inversão da rotação.
10

32. Figura 1.9: Característica do binário Electromagnético e do Escorregamento do Motor Assíncrono
É necessário destacar também que a máquina só pode funcionar de maneira estável apenas
na zona mostrada na figura, uma vez que é estável, na zona em que o binário aumenta com o
aumento de escorregamento. Isto se deve porque, quando a máquina opera como um motor e
aumenta a carga mecânica no eixo, inicialmente se produz uma diminuição de velocidade e um
aumento do escorregamento do motor. Se aumentar o escorregamento o binário diminui, a
diferença entre o binário mecânico da carga e electromagnético é cada vez maior até que o motor
parar. Tem que acontecer, para operar de forma estável, que ao diminuir a velocidade (aumento de
escorregamento) aumente o binário electromagnético para atingir o equilíbrio mecânico. No
funcionamento como gerador a zona instável dá lugar a um aumento progressivo da velocidade.
Esta zona estável é caracterizada por valores muito pequenos de escorregamento, geralmente
menor que 0,1. Como o escorregamento é muito pequeno, é possível fazer algumas aproximações
na equação 1.18.
Primeiramente que: )( '
'
2
1
'
2
drds XX
s
R
eR
s
R
+>>>> . Com esta aproximação a equação 1.18
se converte em:
s
R
V
T
S
em .
.
.3
'
2
2
1
ω
≈ (1.19)
Analisando esta equação conduz à conclusão de que, na zona de funcionamento estável do
motor, o binário electromagnético é proporcional ao escorregamento e como, no estado estável o
binário mecânico da carga é igual ao binário electromagnético, ao aumentar a carga imposta ao
funcionamento da máquina como motor, aumenta o escorregamento e diminui a velocidade. No
funcionamento como gerador, o binário eletromagnético é negativo, quer dizer que, se quiser
aumentar a potência entregue à rede, deve-se, aumentar o binário eletromagnético e o valor
11

33. modular do escorregamento, mas, como este escorregamento é negativo nesta zona, a velocidade
deve aumentar.
Nas características se mostram alguns valores para os quais é importante para determinar a
sua expressão. É de grande importância conhecer o binário máximo do motor, pois define sua
capacidade de sobrecarga. Este é o valor para o qual a inclinação característica muda de positivo a
negativo.
Como o binário electromagnético é proporcional à potência consumida na resistência
s
R'
2
de acordo com a equação 1.15, o binário máximo ocorre quando a energia consumida por esta
resistência é máxima, o que acontece quando seu valor óhmico é igual a do resto da impedância do
circuito equivalente aproximada do tipo em L, ou seja, quando,
2'2
1
2
'
)( drds XXR
s
R
++=
e,
portanto o escorregamento para o binário máximo, trabalhando como motor é:
2'2
1
'
2
)( drds
M
XXR
R
s
++
= (1.20)
Como:
2'
1
2
1 )( drds XXR +<<
Então:
)( '
1
2
'
drds
M
XX
R
s
+
≈ (1.21)
Substituindo a equação 1.20 em 1.18 se obtém o valor do binário máximo como motor é:
])(.[.2
.3
2'
1
2
1
2
1
2
1
max
drdsS
m
XXRR
V
T
+++
=
ω
(1.22)
É aproximadamente:
).(.2
.3
'
1
2
1
max
drdsS XX
V
T
+
≈
ω
(1.23)
Como gerador, o escorregamento é negativo e a expressão fica então da seguinte forma:
])(.[.2
.3
2'
1
2
1
2
1
2
1
max
drdsS
g
XXRR
V
T
++−
=
ω
(1.24)
12

34. Vesse que o binário máximo como motor é ligeiramente menor que o binário máximo como
gerador.
Se dividir-se a equação 1.18 com a 1.24 se obtém:
[ ]
2'2
'
2
1
'
22'2
11
max
)()(
).()(.2
drds
drds
m
em
XX
s
R
R
s
R
XXRR
T
T
+++
+++
=
Utilizando esta expressão e fazendo
drds XX
R
a '
1
+
= , obtém-se:
[ ]






+++
++
=
s
s
s
s
aa
aa
T
T
M
M
em
.1.2
1.2
2
2
max (1.25)
Em muitos casos, sobre tudo nas máquinas de potência média e grande, R1 que é quase
igual à resistência do estator, é muito pequena em comparação com a reactância total e o
coeficiente “a” é desprezível, sendo a equação 1.25 de uma forma aproximada, conhecida como
Fórmula de Kloss:
s
s
s
sT
T
M
M
em
+
≈
2
max (1.26)
CAPÍTULO II
ARRANQUE E PARAGEM DE MOTORES ASSINCRONOS
2.
2.1. INTRODUÇÃO
O processo que decorre desde que um motor eléctrico é ligado à rede, até atingir a sua
velocidade e corrente estável de acordo ao mecanismo accionado, é chamado de Processo de
Arranque e impõe ao motor e a seu sistema de alimentação e controlo determinados os requisitos
gerais para qualquer motor e específicos dependendo do tipo de motor. Estes requisitos podem ser
classificados em três tipos:
 Os que impõe a rede eléctrica;
 Os que impõe o próprio motor;
 Os impostos pela carga mecânica ao mecanismo accionado acoplado ao eixo do motor.
13

35. Quanto à rede eléctrica, ao arrancar o motor não deve provocar quedas de tensão
importantes que afectam o funcionamento de outras cargas eléctricas existentes na rede nem
provocar curto circuito ou outros fenómenos transitórios prejudiciais ao redor do motor.
Quanto ao motor em si, a corrente que circula no arranque não deve causar aquecimento
excessivo que pode danificar o isolamento nem danificar algumas das suas partes que obrigam a
uma reparação e manutenção muito frequente.
Quanto ao mecanismo accionado, por uma parte, no arranque o motor deve fornecer a este
mecanismo o binário necessário para colocá-lo em movimento e alcançar um estado estável num
tempo razoável de acordo com o processo de produção que faz parte do mecanismo, sobre tudo se
este processo requer arranque frequente. Por outra parte, o binário de arranque não pode ser muito
grande nem ter picos muito elevados que danificam o mecanismo accionado ou prejudicam o
processo de produção, como por exemplo, num tear onde um pico de binário muito grande pode
quebrar a fiação da máquina.
Como pode ser visto, os efeitos na rede tem a ver com a tensão, os problemas no motor com
a corrente e os problemas no mecanismo accionado com o binário produzido.
No caso dos motores de corrente contínua, não se permite uma corrente de arranque superior
que 1,5 a 2 vezes o valor nominal, porque uma maior corrente pode danificar o colector e as escovas
e tirar o motor de serviço. Quanto à rede, estes motores funcionam com conversor estático que
controlam e limitam automaticamente a corrente no motor e consequentemente na rede, produzindo
também um arranque suave. Em este tipo de motores, que são arrancados com corrente de excitação
máxima e constante, o binário produzido em por unidade é praticamente igual à corrente em por
unidade, ou seja, que produz um binário de arranque de 1,5 a 2 vezes ao nominal, ao qual quase
sempre é suficiente para pôr em movimento a carga. Se o motor de corrente contínua é do tipo em
série, se produz, com a mesma corrente, um binário ainda maior. Por isso, este tipo de motores é
utilizado em comboios eléctrico que têm que mover cargas de muita inércia que de outra forma faria
o arranque demorar muito tempo com uma corrente elevada.
2.2. ARRANQUE DE MOTOR ASSÍNCRONO
Para analisar o processo de arranque do motor assíncrono é feita referência ao circuito
equivalente do motor apresentado na figura 1.8 do Capítulo 1. No caso do arranque o
escorregamento (s) é igual a 1 e a corrente de vazio (Io) é muito menor do que a referida corrente do
rotor e o circuito equivalente é tal como se mostra na figura 2.1.
14

36. Figura 2.1: Circuito equivalente do Motor Assíncrono no Arranque.
De acordo a este circuito, a corrente de arranque é igual a:
2
21
2'
21
1'
21
)()( dd
arr
XXRR
V
III
+++
=== (2.1)
O parâmetro mais importante para determinar as características de funcionamento do
circuito equivalente, tanto em estado estacionário como transitória é a resistência do rotor, neste
caso, referida ao estator (R2
'
). Como pode ser visto a partir da equação 2.1, uma resistência do rotor
relativamente alta dá lugar a uma redução da corrente de arranque. Também do ponto de vista do
binário de arranque é conveniente uma resistência do rotor não muito pequeno pois ao aumentar a
resistência do rotor aumenta a componente de corrente do rotor em fase com a tensão que é a que
produz o binário por ser a componente activa, embora diminuía seu valor absoluto. Isto é
claramente visível na figura 2.2. Como pode ver-se, uma resistência pequena dá lugar a um ângulo
de factor de potência do rotor grande e uma componente em fase Oa, enquanto que uma resistência
mais alta diminui o ângulo de factor de potência aumentando a componente em fase, neste caso Ob,
ainda que o valor absoluto da corrente diminuiu.
Figura 2.2: Diagramas Fasoriais do Motor para Diferentes Resistências do Rotor.
Ou seja que, do ponto de vista do arranque convém que o rotor tenha uma alta resistência,
por isso não é conveniente do ponto de vista das características de funcionamento do motor já que
aumenta as perdas no rotor e diminui o seu rendimento ou eficiência.
Se pretendermos uma solução de compromisso com uma resistência do rotor que não seja
nem muito alta nem muito pequena, se obtém um motor com um rendimento relativamente baixo e
um binário de arranque não muito alto. Portanto, a solução está em encontrar a forma de ter uma
alta resistência no momento de arranque e uma baixa resistência em funcionamento normal depois
de atingir o estado estacionário. Existem duas soluções gerais:
 Utilizar um motor de indução de rotor bobinado inserindo resistências variáveis no rotor;
 Utilizar um motor de indução de gaiola de esquilo com resistência do rotor variável de
acordo com o escorregamento.
Motor de Rotor Bobinado com Resistência de Rotor Variável: O motor de rotor bobinado
se caracteriza por ter um enrolamento trifásico no rotor idêntico ao do estator, mas ligado a três
15

37. anéis deslizantes sobre os quais se encontram três escovas que permitem introduzir resistências
externas. O esquema eléctrico é mostrado na figura 2.3. Para arrancar o motor se liga ao disjuntor
C1 com C2, C3 e C4 aberta. Isso faz com que o motor arranca com uma resistência relactivamente
alta no rotor que limita a corrente e fornece um bom binário de arranque. Passando um tempo o
motor adquirir certa velocidade, fecha C2 com o qual a resistência diminui e a velocidade aumenta.
Passado uma vez mais o tempo se fecha C3 e depois do mesmo processo se fecha C4 com o qual o
motor entra em funcionamento estacionário com uma baixa resistência no rotor já que está sem
resistências externas. O processo é gradual e por passos para evitar grandes picos de corrente.
Figura 2.3: Esquema do Circuito de Arranque do Motor de Rotor Bobinado.
O processo de variação das características mecânicas do motor é mostrado na figura 2.4. O
binário máximo permanece constante já que, de acordo com as equações 1.22, 1.23 e 1.24 não
depende da resistência do rotor. O que depende da resistência do rotor é o escorregamento a qual
ocorre este binário máximo.
16

38. Figura 2.4: Variação das Características Mecânicas do Esquema da figura 2.1
Do ponto de vista técnico, este método é muito eficaz para limitar a corrente de arranque e
aumentar o binário de arranque, mas tem a desvantagem de que necessita de utilizar um motor de
rotor bobinado mais caro e a manutenção necessária é a mesma que uma de gaiola de esquilo. Por
causa disso usa-se somente como mecanismo de arranque muito crítico e complicado.
Motor de Gaiola de Esquilo com Resistência do Rotor em Função do Escorregamento: No
caso do rotor de gaiola, os condutores do rotor são barras profundas ou estão compostos por dois
tipos de barras como se mostra na figura 2.5. Isto se faz para que os parâmetros do rotor não sejam
iguais em condições normais de funcionamento quando o escorregamento é menor do que no
arranque ou seja, quando o escorregamento é igual a 1. Para isto se aproveita o chamado Efeito
Pelicular que faz com que, com corrente contínua ou alternada de frequência muito baixa, a
corrente se distribua uniformemente em todo condutor, mas quando se vai aumentando a
frequência, a densidade da corrente é maior na zona acima e isto é equivalente a uma diminuição da
área efectiva e a um aumento da resistência. Outras vezes o rotor possui duas barras:
 De elevada resistência que atua no arranque
 De baixa resistência que actua em condições normal de funcionamento.
Com isto se consegue que no arranque
(escorregamento igual a 1) a resistência seja alta e aumente o binário de arranque limitando-se a
corrente de arranque em funcionamento normal e estacionário (escorregamento muito pequeno) a
resistência seja baixo permitindo um funcionamento eficiente do motor. Deve assinalar-se também
que com a reactância de dispersão do rotor acontece o contrário é menor no arranque e maior em
condições normais.
17

39. Figura 2.5: Barras do Rotor no Motor Assíncrono de Gaiola de Esquilo.
Aqui também é importante assinalar que entre os dados do catálogo do motor há duas que se
referem ao arranque que são:
 Binário máximo Tmax / Tn oscila entre 1,5 e 2,8;
 Corrente de arranque em por unidade Iarr / In oscila entre 5,5 e 8.
Deve assinalar-se que existem motores que são construídos com um motor de alta
resistência, tanto em arranque como em funcionamento normais, são os chamados de Alto Binário
de Arranque e Alto Escorregamento cuja eficiência em funcionamento normal é baixa. Estes
motores são usados em aplicações muito específicas, tais como as gruas de indústria metalúrgica
que não trabalham de forma contínua (não muito interessado na eficiência ou rendimento) e exigem
elevados binário de arranque, devido às condições difíceis no arranque.
Como se disse anteriormente, a característica mecânica de um motor de gaiola de esquilo
depende, principalmente, e mais que de qualquer outra coisa, da construção do seu rotor, ou seja do
valor da resistência da gaiola e sua variação com o escorregamento.
2.2.1. Métodos de Arranque de Motor Assíncrono Gaiola de Esquilo
Em geral existem três métodos de Arranque de motor de indução de gaiola esquilo:
 Método de Arranque Directo a Rede;
 Método de Arranque a Tensão Reduzida;
 Método de Arranque a Frequência Variável.
Método de Arranque Directo: No método de arranque directo à rede o motor é ligado
diretamente à rede no momento de arranque sem qualquer dispositivo intermediário. É o que leva
menos inversão inicial e, portanto, deve ser realizada quando não se justifiquem os métodos de
tensão reduzida. É usado principalmente em motores de pequeno porte cujo arranque não provoca
uma queda de tensão apreciável na rede. Os valores de binário de arranque e corrente de arranque
são os que veem no catálogo do motor.
18

40. Arranque a Tensão Reduzida: Quando se trata de um motor relativamente grande em
relação à capacidade da subestação que alimenta o Centro de Controlo de Motores donde se
encontra localizado, o arranque directo geralmente provoca uma queda de tensão significativa na
rede e é necessário reduzir esta corrente de arranque. Tratando-se de um motor que move uma carga
proporcional à velocidade, tais como, por exemplo as bombas, compressores centrífugos e
ventiladores se reduz esta corrente de arranque reduzindo a tensão aplicada no motor.
Existem três métodos de arranque a tensão reduzida:
 Arranque por Autotransformador;
 Arranque Estrela-Triangulo;
 Arranque suave com Conversor Estático (Soft Starter).
Se o motor movimenta uma carga de binário constante o que requer elevado binário no
arranque, estes métodos não são aplicáveis, pois se na equação 1.18 igualarmos a 1 o valor do
escorregamento, veremos que o binário de arranque é proporcional ao quadrado da tensão, pelo
qual, se por exemplo, se diminuir a tensão à metade, a corrente de arranque é a metade agora, mas o
binário de arranque é a quarta parte.
Na figura 2.6 mostra-se o esquema de arranque por autotransformador. Ao arrancar o motor,
ligando-o à rede trifásica, se fecham os contactos 1 e 3 deixando o autotransformador em estrela e a
tensão aplicada ao motor se reduz do valor Vn a Vred. Portanto, a relacção de transformação do
autotransformador é:
red
n
red
V
V
k = (2.2)
Ao aproximar-se a velocidade estacionária do motor, se abrem os contactos 1 e 3 e
posteriormente se fecha o contacto 2 para deixar o motor ligado à tensão nominal.
Figura 2.6: Esquema de Arranque por Auto Transformador.
19

41. Supõe-se que a corrente de arranque a tensão nominal é Iarrn e a corrente de arranque tensão
reduzida é Iarred. É importante ressaltar que a relação entre essas duas correntes é o Factor de
Redução de Corrente de Arranque que é o que nos interessa calcular. No arranque, a relação entre
a corrente da rede e a corrente do motor é:
redmot
arred
kI
I 1
= (2.3)
Também é verdade que a redução da corrente do motor é proporcional à redução da tensão,
ou seja:
red
arrn
mot
k
I
I = (2.4)
Combinando as equações 2.3 e 2.4 se obtém o fator de redução de corrente para este
método:
2
1
redarrn
arred
rc
kI
I
K == (2.5)
Uma vez que o binário é proporcional ao quadrado da tensão, a redução do binário é
também igual a:
2
1
red
rb
k
K = (2.6)
Figura 2.7: Arranque Estrela-Triângulo.
Na figura 2.7 se mostram os enrolamentos do motor no arranque estrela-triângulo. A ligação
à rede é feita através dos contactos 1 que permanecem sempre fechados. O arranque se faz com os
enrolamentos ligado em estrela com os contactos 3 fechados e os 2 abertos. Ao aproximar-se à
condição estacionária de funcionamento se abrem os contactos 3 e se fecham os 2 funcionando o
motor em triângulo. O motor deve estar projectado para funcionar em triângulo em estado
estacionário. Como é evidente, o factor de redução da tensão aqui é 3 e então, aplicando a
equação 2.5 e 2.6 a corrente e o binário é reduzido a 1/3.
20

42. Figura 2.8: Regulador de Tensão Estático Utilizado nos Soft Starters.
Os arrancadores Suaves ou Soft Starters são dispositivos que permitem variar a tensão de
forma suave e continua evitando assim os elevados picos de corrente. Utilizam um conversor
estático de tensão como o mostrado na figura 2.8. O ângulo de disparo dos tirístores vai diminuindo
suavemente de acordo ao ajuste feito no controlo do equipamento. Quando se chega à tensão
nominal, os três tirístores em antiparalelo se curto-circuitam como se pode ver na figura 2.8. Na
figura 2.9 mostra-se uma comparação entre o comportamento da corrente nos três métodos de
arranque gerais analisados até agora. Como se pode ver, este método tem a vantagem de permitir
uma limitação de corrente muito mais elevada e evita os elevados picos de corrente. A
desvantagem é que demora mais tempo ao arranca, mas geralmente acontece que este tipo de
arrancadores é utilizado em bombas e compressores centrífugos que não arrancam mais de três
vezes ao dia para o qual a demora em alcançar o estado estacionário não constitui um problema.
Figura 2.9: Comparação das Correntes no Arranque com Diferentes Métodos.
Com este método pode programar-se uma aceleração em rampa programando uma rampa de
variação da tensão. Esta variação é mostrada na figura 2.10, donde se vê que este dispositivo
também permite uma paragem suave mediante uma desaceleração em rampa.
21

43. Figura 2.10: Variação da Tensão Aplicada no Soft Starter Programado com Rampas de Aceleração e Desaceleração.
Outra opção importante é a Limitação de Corrente Fixa na qual se fixa um valor de corrente
que é mantida pelo sistema de controlo automático do arrancador. Geralmente se limita a corrente a
quatro vezes a corrente nominal. Uma limitação maior geralmente não é possível, porque o binário
produzido não é suficiente para mover a carga. Esta situação é mostrada no diagrama da figura
2.11.
Figura 2.11: Variação da Corrente com Ajuste de Limitação de Corrente Fixa.
Na figura 2.12 mostra-se o aspecto externo de um Arrancador Suave com seus componentes
e ajustes. Deve assinalar-se que este equipamento também contém as protecções do motor tanto de
sobre corrente como de sobre carga, falta de fase, sequência invertida e defeito à terra.
22

44. Figura 2.12: Vista Externa de um Arrancador Suave com Seus Ajustes.
Arranque a Frequência Variável: Quando o motor eléctrico tem um controlo de
velocidade por variação de frequência é possível arranca-lo pelo método mais eficaz do ponto de
vista técnico e que é aplicável a qualquer tipo de carga mecânica ou mecanismo accionado que é a
variação suave da frequência aumentando simultaneamente a tensão com a frequência.
Programa-se o arranque do motor de tal maneira que a frequência e a tensão vão
aumentando progressivamente (em forma de rampa ou em S) até alcançar a velocidade desejada,
permite também um limite de escorregamento, que faz com que em todo instante se trabalhe na
zona estável da característica mecânica do motor. Nesta zona o factor de potência do rotor é alto e
se consegue um determinado valor de binário, com uma corrente relativamente baixa. Isto não só
provoca a redução da corrente de arranque, mas também um "achatamento" dos picos de binário,
que protege o mecanismo accionado.
A figura 2.13 apresenta a variação da frequência de um arranque em rampa e um arranque
em S. São usados com o objetivo de tornar o arranque mais suave. Os variadores de velocidade
modernos permitem o ajuste à vontade da inclinação da rampa de arranque, parada ou dos
parâmetros do arranque em S. Este último é utilizado em cargas críticas que podem ser danificadas
com picos de binário elevado, tais como os utilizados na indústria têxtil e outros.
Figura 2.13: A Variação da Frequência Inicial e Começar Rampa S.
23

45. Como é sabida, a equação dinâmica do accionamento é:
c
M
em T
dt
d
JT +=
ω
(2.7)
Onde:
Tem – Binário electromagnético produzido pelo motor;
Tc – Binário mecânico de oposição do mecanismo accionado;
J – Inércia total do motor e a carga.
Por outro lado, a velocidade do rotor é igual a:
sM 11 ωωω −= (2.8)
Onde:
ω1 – Velocidade síncrona;
s1ω – Escorregamento absoluto ou frequência de escorregamento.
Substituindo a equação (2.8) em (2.7) e resolvendo o binário dinâmico se obtém:
dt
d
J
dt
d
JTTT s
cemdin
11 ωω
−=−= (2.9)
O binário dinâmico tem dois componentes:
 Uma proporcional a velocidade de troca da frequência, ou seja, a inclinação da rampa de
aceleração (este valor é selecionável pelo usuário nos variadores de velocidade
industrial);
 Outra proporcional à variação do escorregamento.
Este último valor é, geralmente, quase zero já que o escorregamento geralmente mantem-se
quase constante e igual ao nominal. Isto quer dizer que, quanto maior o declive da rampa de
aceleração, maior será o binário dinâmico e mais rápido é o arranque.
Deve assinalar-se que, embora este tipo de arranque é melhor do ponto de vista técnico,
instalar um variador de velocidade somente para o arranque do motor não se justifica
economicamente.
24

46. 2.3. PARAGEM DE MOTOR ASSÍNCRONO
Denomina-se paragem de um motor ou accionamento eléctrico ao processo durante o qual a
velocidade do motor diminui quando sujeita a uma desaceleração ou aceleração negativa. Este
processo pode ou não ser intencional. Se o motor estiver desligado da rede, ou existe um comando
de desaceleração por parte do operador, a paragem é intencional, mas se for problema de proteção
que desliga o motor da rede ou simplesmente aumenta a carga e o motor desacelera a paragem não é
intencional.
dt
d
JTTT M
dincem
ω
==− (2.10)
Colocando a equação 2.7 sob a forma mostrada na equação 2.10 veremos que para ocorrer
uma aceleração negativa é necessário um binário dinâmico negativo e para isso o binário
electromagnético Tem deve ser menor do que o binário mecânica Tc da carga.
Se desligarmos o motor de sua fonte de alimentação (que pode ser a rede ou um conversor
estático), a corrente torna-se zero ou igual ao binário electromagnético e ao processo de
desaceleração ou paragem é dirigida exclusivamente pela inércia e características mecânicas
resistivas da carga ou mecanismo accionado. Este tipo de paragem é conhecido como Paragem
Livre.
Em ocasiões, para que solicita o processo de produção onde se encontra o motor ou por
razões de segurança, é necessário parar ou desacelerar rapidamente o motor e não se pode permitir a
paragem livre. Neste caso deve ser negativo o binário electromagnética Tem ou mais exatamente o
binário electromagnético deve ter um sentido oposto ao da velocidade. Isto é chamado de Paragem
Forçada e será a que se tratará de agora em diante com o nome genérico de Paragem.
2.3.1. Tipos de Paragem de Motor Assíncrono
Existem três tipos de paragem nos motores assíncronos em geral, nos accionamentos e
motores eléctricos:
 Paragem Regenerativa;
 Paragem Dinâmica;
 Paragem Por Inversão ou Contracorrente.
Paragem Regenerativa: A paragem regenerativa se caracteriza porque a diminuição da
energia cinética que se produz ao diminuir a velocidade se reintegre à rede (retirado por supostas
perdas de potência no motor e seu esquema de alimentação) e é recuperada.
Este é o caso das cargas ou mecanismos submetidos à acção da gravidade como as gruas,
elevadores e veículos eléctricos. Por exemplo, em um elevador que baixa com muitas pessoas na
cabine, a cabine pesa mais do que o contrapeso e se o motor não está ligado a sua alimentação a
25

47. cabine se acelera rapidamente e provoca um acidente. Se estiver ligado à rede de alimentação uma
parte da energia cinética é devolvida à rede permitindo que a velocidade se estabilize.
Este é o caso dos motores assíncronos alimentados por variadores de velocidade com
conversores do tipo regenerativo ou Back to Back, o circuito mostrado na figura 2.14. Como se
pode ver, consistem de dois conversores um lado do motor e outro do lado da rede. Normalmente,
se a máquina funciona como um motor, o conversor do seu lado funciona como inversor e o do lado
da rede como rectificador, ambos controlados. Quando se trabalha em paragem regenerativa, a
máquina funciona como gerador, o conversor do seu lado como um rectificador e do lado da rede,
como inversor invertendo-se o fluxo de energia que agora vai da máquina aos conversores e se
entrega à rede.
Figura 2.14: Esquema do Conversor Back to Back
Para explicar como funciona a paragem regenerativa neste caso se faz referência à figura
2.15 onde se mostra duas características mecânicas do motor no primeiro e segundo quadrantes:
 A primeira característica é para um determinado valor de frequência e a tensão f1 e V1.
 A segunda característica para outros valores de frequência e tensão V2 e f2 mais baixas,
ou seja, f2 < f1 e V2 < V1.
Primeiro se supõe que se move uma carga do tipo passiva, ou seja, cujo binário mecânico Tc
sempre se opõe ao sentido de rotação. No instante inicial, a máquina funciona como motor a uma
velocidade ωM1 na primeira caracteristica, o conversor do lado do motor como inversor e conversor
do lado da rede como retificado. A energia flui da rede ao motor. Se agora se dá um comando de
diminuição de frequência tal que se passa a funcionar na segunda característica, a velocidade não
pode mudar instantaneamente com o qual se passa produzir o binário eletromagnético T1 positivo e
no sentido da velocidade o binário eletromagnética T2 negativo e, portanto, contrário à velocidade.
Como agora está a funcionar no segundo quadrante, a máquina funciona como gerador, o conversor
do seu lado como retificador e do lado da rede como inversor e a energia flui transitoriamente da
máquina aos conversores para a rede. Isso faz com que o motor pará rapidamente, invertendo-se o
sentido do binário electromagnético e, se for uma carga de binário constante, passa a funcionar
novamente como motor com o mesmo binário anterior T1 mas agora a uma velocidade estacionária
ωM2 mais baixa. Com cargas passivas funciona como gerador da máquina somente pode se produzir
26

48. de forma transitória dando origem, graças a paragem regenerativa a uma diminuição da velocidade
mais rápida.
Se funcionar com uma carga activa tal como um elevador, este pode está a funcionar
subindo o elevador cheio com o binário T1 e a velocidade ωM1 e se a cabine do elevador se esvaziar
o contrapeso do elevador pesa mais do que a cabine, o binário mecânico se inverte e o
eletromagnético tem que ser também sendo agora T2, mas a velocidade seria agora maior ou igual a
ωM3. Se a frequência for diminuída de f1 para f2 a velocidade diminui ωM3. Neste caso, a máquina
funciona como gerador em estado estável e se considera como paragem desde o ponto de vista que
está operação como gerador impede a aceleração descontrolada da cabine do elevador ao subir.
Figura 2.15: Características Mecânicas do Motor Assíncrono com paragem Regenerativa
Paragem Dinâmica: A paragem dinâmica consiste em pôr a funcionar a máquina como
gerador invertendo o sendo do binário eletromagnético que se opõe agora a velocidade, levando
rapidamente à velocidade a zero. A energia cinética que foi armazenada no rotor em suas massas
rotativas se dissipada na resistência interna do motor. Nos motores assíncronos este tipo de paragem
se realiza desligando o motor da rede e ligando a uma fonte de corrente continua, conforme é
mostrado na figura 2.16. Em funcionamento normal K1 estão fechados e os KF abertos. Para parar
se abri K1 desligando o motor, da rede e se fecha KF com o qual se alimentam com corrente
continua duas fases do estator. A resistência de paragem limita a corrente continua aplicada.
Figura 2.16: Esquema de Paragem Dinâmica de um Motor Assíncrono.
27

49. Ao aplicar corrente continua se cria um fluxo estacionário no entreferro da máquina. Como
ele está girando, os condutores do rotor cortam este fluxo. Induz-se uma fem nas mesmas e circula
uma corrente que ao relaccionar com o fluxo produz o binário electromagnético necessário para
paragem.
Se a velocidade do rotor é regulada com um variador de velocidade variável, a paragem
dinâmica se realiza inserindo uma resistência de paragem Rfr tal como se mostra no circuito da
figura 2.17. Para parar se retiram os pulsos de travão do inversor trifásico e um pulso é enviado para
o transístor ou IGBT de paragem em série com a resistência isso faz com que a corrente contínua
circula da forma como é apresentada na figura. A paragem pode ser controlada, variando o tempo
de ligar e desligar o transístor de paragem com qual se varia o valor equivalente da resistência de
paragem.
Figura 2.17: Esquema de Paragem Dinâmica com o Motor Alimentado por um Conversor Estático.
Neste tipo de sistemas com conversores é possível também a paragem com corrente contínua
com um circuito, como o que é mostrado na figura 2.17.
Figura 2.18: Paragem por Aplicação de Correntes Continua com o Motor Alimentado por Conversor Estático.
28

50. Paragem por Inversão ou Contracorrente: A paragem por inversão ou contracorrente se
produz quando se inverte a sequência das tensões aplicadas ao motor. Isto faz com que,
imediatamente, o campo magnético rotativo inverte seu sentido e se opõe à velocidade criando um
binário de paragem muito alto que diminui muito rapidamente a velocidade do motor. Se não for
desligado da rede ao passar a velocidade por zero com um interruptor centrífugo ou sensível à
rotação, o motor arranca no sentido oposto.
A figura 2.19 apresenta o esquema usado para este tipo de paragem. Se supõe que o motor
funciona no estado estacionário com os contactos K1 fechados e K2 abertos e supõe-se girar em
sentido horário. Para aplicar a paragem se abre K1 e imediatamente depois se fecha K2 invertendo-
se desta forma a sequência das tensões aplicadas.
Neste tipo de paragem tanto a energia eléctrica de entrada como a energia mecânica cinética
que vem através do eixo se dissipa no rotor por isso, no caso dos motores de gaiola de esquilo não
deve ser aplicado frequentemente e nos motores de rotor bobinado se aplicada com toda a
resistência externa incluída no rotor para limitar a corrente.
Figura 2.19: Esquema de paragem por Inverso
29

51. CAPÍTULO III
MODELO MATEMATICO DO MOTOR ASSÍNCRONO
3.1. INTRODUÇÃO
No capítulo 1, foi descrito as características construtivas e o princípio de funcionamento do
motor assíncrono trifásico e utilizou-se como modelo o denominado Circuito Equivalente. Este
modelo só é aplicável apenas para analisar o comportamento do motor no estado estacionário. No
entanto, neste capítulo se vai analisar o processo de arranque e paragem que são os processos
dinâmicos ou transitórios, nos quais não se pode aplicar o modelo de circuito equivalente, para a
determinação das características do motor no estado estacionário.
Será necessário, portanto, utilizar um modelo dinâmico que tenha em conta as variações
transitórias tanto das correntes, como da velocidade e o binário. Este modelo permitirá uma analisa
do comportamento do motor no arranque e paragem a partir de uma linguagem de simulação
apropriada como é o SIMULINK do MATLAB. Deve notar-se que este software possui na
ferramenta SimPowerSystem um modelo do motor assíncrono que não consideramos apropriados
pois considera constantes os parâmetros do rotor e como já se explicou, precisamente a variação
destes parâmetros com o escorregamento desempenha um papel importante no processo de arranque
e paragem. Portanto, o modelo utilizado para esta tese irá considerar esta variação dos parâmetros
do rotor com o deslizamento.
3.2. EQUAÇÕES DO MODELO
A figura 3.1 abaixo é uma repetição da figura 1.1 do capítulo 1 sobre o qual será baseada a
escritura das equações. Como é conhecido, e é mostrado na figura, este tipo de motor pode ser
considerado, como composto por três bobinas no estator, localizados a 120o
graus eléctricos entre si
e três enrolamentos do rotor também localizado a 120o
graus eléctricos. Obviamente, os
enrolamentos do rotor estão em movimento em relação ao estator.
Figura 3.1: Corte Transversal Esquemático do Motor Assíncrono
30

52. Na abordagem deste modelo serão consideradas as seguintes suposições iniciais:
 O campo magnético do entreferro distribui-se senoidalmente.
 Analisa-se uma máquina de 2 polos, embora os resultados são aplicáveis a uma de P
polos.
 Os enrolamentos do estator e do rotor são simétricas e as três fases de cada uma deles
estão situados a 120º grau eléctrico no espaço.
 Despreza-se a saturação e a histerese.
 As perdas de aço no estator e no rotor são desprezadas.
 Os parâmetros do rotor supõem-se referidos ao estator.
Cada um dos seis enrolamentos da máquina (três fases do estator e três fases do rotor) nos
permite escrever a equação fundamental da tensão (u) dos circuitos das máquinas eléctricas:
dt
d
iRu
ϕ
+= . (3.1)
Onde:
R – Resistência de cada enrolamento;
I – Corrente que circula por intermédio dele;
Φ – Fluxo do enrolamento ligado correspondente.
Inicialmente deve se determinar as equações do fluxo concatenado, que são produzidas em
cada enrolamento ou fase pela sua própria corrente e pela corrente dos outros enrolamentos.
As concatenações do fluxo dos enrolamentos ou fases do estator são:
cAcbAbaAaCACBABAAAA iLiLiLiLiLiL ).().().(... θθθϕ +++++= (3.2a)
cBcbBbaBaCBCBBBABAB iLiLiLiLiLiL ).().().(... θθθϕ +++++= (3.2b)
cCcbCbaCaCCCBCBACAC iLiLiLiLiLiL ).().().(... θθθϕ +++++= (3.2c)
E as do rotor:
cacbabaaaCaCBaBAaAa iLiLiLiLiLiL ...).().().( +++++= θθθϕ (3.3a)
cbcbbbabaCbCBbBAbAb iLiLiLiLiLiL ...).().().( +++++= θθθϕ (3.3b)
cccbcbacaCcCBcBAcAc iLiLiLiLiLiL ...).().().( +++++= θθθϕ (3.3c)
Onde:
CCBBAA LeLL ,, – São autoindutâncias ou indutâncias próprias, que são
constantes é igual a:
31

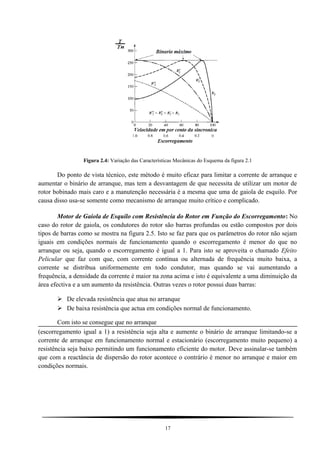
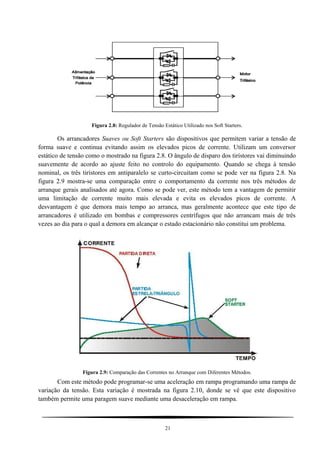
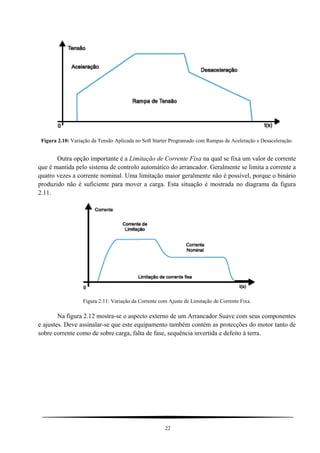
53. L L L L L LAA BB CC fs m sm= = = + = (3.4a)
O mesmo pode ser dito para indutâncias próprias do rotor:
L L L L L Laa bb cc fr m rm= = = + = (3.4b)
Onde:
fyfs LeL – São as indutâncias de filtração do estator e o rotor;
mL – Indutância magnetizante correspondente ao fluxo mutua que atravessa ambos
os enrolamentos. Devido à simetria magnética existente tanto no estator como no rotor, estas
indutâncias são constantes e não dependem da posição de este último.
Pela mesma causa, as indutâncias mútuas entre os três enrolamentos do estator também são
iguais e independentes da posição:
2
)
3
2
(cos m
mCBBCCAACBAAB
L
LLLLLLL −=======
π
(3.5a)
O mesmo acontece com o rotor:
2
)
3
2
(cos. m
mcbbccaacbaab
L
LLLLLLL −=======
π
(3.5b)
A indutância mutua entre os enrolamentos do estator e os do rotor dependem entre si da
posição e são iguais a:
)(cos. θmCcBbAa LLLL === (3.6a)
)
3
2
(cos.
π
θ +=== mCaBcAb LLLL (3.6b)
)
3
2
(cos.
π
θ −=== mCbBaAc LLLL (3.6c)
Substituindo nas equações (1.10), (1.9) e (1.8) em (1.6) e (1.7) obtém-se:
)]
3
2
(cos.)
3
2
(cos.)(cos..[.
π
θ
π
θθϕ −++++= cbamASA iiiLiL (3.7a)
)]
3
2
(cos.)(cos.)
3
2
(cos..[.
π
θθ
π
θϕ +++−+= cbamBSB iiiLiL (3.7b)
)](cos.)
3
2
(cos.)
3
2
(cos..[. θ
π
θ
π
θϕ cbamCSC iiiLiL +−+++= (3.7c)
aRCBAma iLiiiL .)]
3
2
(cos.)
3
2
(cos.)(cos..[ +++−+=
π
θ
π
θθϕ (3.8a)
32

54. bRCBAmb iLiiiL .)]
3
2
(cos.)(cos.)
3
2
(cos..[ +−+++=
π
θθ
π
θϕ (3.8b)
cRCBAmc iLiiiL .)](cos.)
3
2
(cos.)
3
2
(cos..[ ++++−= θ
π
θ
π
θϕ (3.8c)
Nestas equações:
L L LS fs M= + (3.9a)
L L LR fr M= + (3.9b)
L LM m=
3
2
. (3.9c)
Estas indutâncias são as mesmas que aparecem no circuito equivalente do motor.
Como se pode ver, as equações das ligações do fluxo são extremamente complicadas,
principalmente porque são funções não lineares da posição do rotor θ E ao aplicar a equação da
tensão 1, onde aparece a sua derivada a complicação torna-se ainda maior. Então, explica-se os
passos seguintes para simplificar essas equações e torná-las mais fáceis de gerenciar.
Devido ao carácter trifásico deste motor, tanto o rotor como o estator, é um primeiro passo
para simplificar as expressões das equações, desenvolver um modelo baseado no chamado Vector
Espacial Trifásico na qual considera uma única entidade matemática das três fases. A sua definição
para o caso das correntes é a seguinte:
)...(
3
2 2
CBA iaiaii

++= (3.10)
Onde:
iA, iB e iC – São as correntes para as três fases e definem também os três vectores
unitários.
 Para a fase A:
o
j
e 0
1 =

 Para a fase B:
o
j
ea 120
=

 Para a fase C:
o
j
ea 1202 −
=

A representação gráfica do vector se mostra na figura 3.2.
33

55. Figura 3.2: Vector Espacial Trifásico.
Como se pode ver, a projecção do vector em cada um dos eixos das três fases é o valor
instantâneo da corrente através dessa fase.
Este vector não considera a componente de sequência zero, que pode ser definido como:
).(
3
1
CBAo iiii ++= (3.11)
Se der diferente de zero esta componente, seria subtraído a cada fase do estator.
A partir de agora será sempre o motor conectado em estrela sem neutro acessível, o que
permite assegurar que acorrente de sequência zero seja igual a zero.
Em seguida, se aplicará esse conceito vectorial às equações de concatenações de fluxo
deduzidas acima, mas aplicando antes as equações de Euler:

2
)(cos
θθ
θ
jj
ee −
+
= ;

2
..
)
3
2
(cos
2 θθ
π
θ
jj
eaea −
+
=+

;

2
..
)
3
2
(cos
2 θθ
π
θ
jj
eaea −
+
=−

.
e que:
34

56.  1. 2
=aa

;
 aaa

=22
;
 01 2
=++ aa

Substituindo estas expressões em 7 e 8 obtém-se:
ϕ θ
A S A M
j
aL i L e i= +. . . (3.12a)
b
j
MBSB iaeLiL .... 2θ
ϕ += (3.12b)
c
j
MCSC iaeLiL ....
θ
ϕ += (3.12c)
ϕ θ
a M
j
A R aL e i L i= +−
. . . (3.13a)
bRB
j
Mb iLiaeL .... 2
+= − θ
ϕ (3.13b)
cRC
j
Mc iLiaeL .... += − θ
ϕ (3.13c)
Multiplicando a equação 3.12a e 3.13a por
3
2
; a equação 3.12b e 3.13b por a

3
2
; a
equação 3.12c e 3.13c por
2
3
2
a

, e aplicando a definição do vector espacial trifásico, obtém-se:
θ
ϕ j
RMSSS eiLiL ...

+= (3.14a)
RR
j
SMR iLeiL

... += − θ
ϕ (3.14b)
Estes são os vectores da concatenação do fluxo do estator e do rotor.
Os vectores das concatenações do fluxo do estator e rotor dependem da posição θ. Isso cria
grandes dificuldades na formulação e soluções das equações do motor. A razão pela qual isto
acontece é que os vectores do estator são definidas num sistema de referência ou coordenadas fixas
no estator e no rotor. Para resolvê-lo deve-se referir a todos os vetores a um sistema de referência
comum. Geralmente utilizam-se os três sistemas de referência para a análise dessas máquinas:
 O que esta fixo no estator;
 O que esta fixo no rotor;
 O que gira a uma velocidade síncrona.
O mais importante para uma máquina assíncrona trifásica é o primeiro e o terceiro e será as
que se fará referência. Para analisar como se pode referir um vector de um sistema de referência a
outro, se utilizará a figura 3.3.
35

57. Figura 3.3: Vector Espacial Trifásico em Sistemas de Coordenadas Diferentes.
Seja )(S
i

o vector em coordenadas do estator, )(R
i

em coordenadas do rotor e )(k
i

em
coordenadas síncronas. Por exemplo, se o vector está em coordenadas do estator forma um ângulo
ψ com a referência, enquanto se referir a coordenadas síncronas irá formar um ângulo ( )ψ θ− k
onde θ ωk t= 1. . Portanto é evidente, que se cumpre as seguintes relações:
k
k
jkS
jSk
jRS
jSR
eii
eii
eii
eii
θ
θ
θ
θ
.
.
.
.
)()(
)()(
)()(
)()(




=
=
=
=
−
−
(3.15)
De acordo com esta equação se procederá referir as equações 3.14 das coordenadas do
estator.
Aplicando a segunda equação 3.15 em (3.14a) obtém-se:
)()()(
.. S
RM
S
SS
S
S iLiL

+=ϕ (3.16a)
Multiplicando (3.14b) por e jθ
e aplicando a primeira equação de (3.15) obtém-se:
)()()(
.. S
RR
S
sM
S
R iLiL

+=ϕ (3.16b)
Como se pode ver, as concatenações do fluxo não dependem da posição do rotor.
Para referir as concatenações do fluxo a um sistema que gira a velocidade sincrónica aplica-
se a terceira equação (3.17) a (3.18a) e (3.18b) e obtém-se:
)()()(
)()()(
..
..
k
RR
k
SM
k
R
k
RM
k
SS
k
S
iLiL
iLiL


+=
+=
ϕ
ϕ
(3.17)
36

58. Em seguida reduzem-se as equações vectoriais de tensão, tanto em coordenadas do estator
como em coordenadas sincrónicas.
Se for aplicado a equação (1) para cada uma das fases do enrolamento do estator é obtém-se:
u R i
d
dt
u R i
d
dt
u R i
d
dt
A S A
A
B S B
B
C S C
C
= +
= +
= +
.
.
.
ϕ
ϕ
ϕ
(3.18)
Onde:
RS
– Resistência do enrolamento do estator por fase.
Multiplicando as equações (3.18) por 2/3, 2/3 e 2/3, e aplicando o conceito de vector
espacial trifásico, obtém-se:
dt
d
Riu
S
S
S
S
S
S
S
)(
)()(
.
ϕ


+= (3.19)
Seguindo o procedimento semelhante ao do rotor obtêm-se:
dt
d
Riu
R
R
R
R
R
R
R
)(
)()(
.
ϕ


+= (3.20)
Onde:
RR – Resistência do enrolamento do estator por fase.
Primeiramente estas equações serão levadas a um sistema de referencia fixo no estator. A
equação 3.19 já está assim trabalharemos com a equação 3.20. Fazendo primeiramente que
θ
ϕϕ jS
R
R
R e−
= .)()( 
sendo a sua derivada:
)..(.. )(
)(
)(
)(
dt
d
je
dt
d
e
dt
d jS
R
S
Rj
R
R θ
ϕ
ϕϕ θθ
−+= −− 

(3.21)
Multiplicando a equação 3.20 por e jθ
e aplicando a equação 1.2 do capítulo 1 tanto para as
tensões como para as correntes, obtém-se:
)(
)(
)()(
.. S
RR
S
RS
RR
S
R j
dt
d
iRu ϕω
ϕ 


−+= (3.22)
É interessante analisar os termos desta expressão:
 O primeiro é a diminuição na resistência;
37

59.  O segundo é uma fem de transformação;
 O terceiro é uma fem que depende das concatenações do fluxo do rotor e da velocidade,
é por tanto, uma fem de velocidade, variável de acoplamento eletromecânica.
Portanto as equações vectórias da máquina em coordenadas do estactor seriam as equações
3.19 e 3.22. Cada vector tem uma componente real sobre o eixo denominado α e outra imaginaria
ao eixo denominado β. Portanto, decompondo a parte real e a parte imaginária, estas equações
obtêm-se:
 Para o estator:
dt
d
iRu
dt
d
iRu
s
sSs
s
sSs
β
ββ
α
αα
ϕ
ϕ
+=
+=
.
.
(3.23)
 Para o rotor:
Considerando que a tensão aplicada é igual zero por ser uma máquina de rotor em curto
circuito teremos que:
α
β
β
β
α
α
ϕω
ϕ
ϕω
ϕ
RR
R
RR
RR
R
RR
dt
d
iR
dt
d
iR
..0
..0
−+=
++=
(3.24)
Decompondo a equação16 na parte real e imaginária teremos que:
βββ
ααα
βββ
ααα
ϕ
ϕ
ϕ
ϕ
RRSMR
RRSMR
RMSSs
RMsSs
iLiL
iLiL
iLiL
iLiL
..
..
..
..
+=
+=
+=
+=
Matricialmente obtém-se que:
38

60. 



























=














β
α
β
α
β
α
β
α
ϕ
ϕ
ϕ
ϕ
R
R
S
S
RM
RM
MS
MS
R
R
S
S
i
i
i
i
LL
LL
LL
LL
.
00
00
00
00
(3.25)
E achando a transformada inversa:
39

61. 





































−
−
−
−
=














β
α
β
α
σσ
σσ
σσ
σσ
β
α
β
α
ϕ
ϕ
ϕ
ϕ
R
R
s
s
SM
SM
MR
MR
R
R
s
s
LL
LL
LL
LL
i
i
i
i
.
1
0
1
0
0
1
0
1
1
0
1
0
0
1
0
1
Onde:
.
.
;
.
;
.
2
2
2
M
MRS
M
R
MRS
R
S
MRS
S
L
LLL
L
L
LLL
L
L
LLL
L
−
=
−
=
−
=
σ
σ
σ
(3.27)
Substituindo estas expressões da corrente em 3.23 e 3.24 e considerando que a velocidade
real do rotor em uma maquina de P polo é rm
P
ωω
2
= quando quatro equações diferenciais com
40

62. quatro incógnitas eléctricas que são as das concatenações do fluxo do estator e as do rotor e uma
incógnita mecânica que é a velocidade do rotor:
α
β
β
σ
β
σ
β
α
α
σ
α
σ
β
β
σ
β
σ
β
α
α
σ
α
σ
α
ϕω
ϕ
ϕϕ
ϕω
ϕ
ϕϕ
ϕ
ϕϕ
ϕ
ϕϕ
Rm
R
R
S
R
S
M
R
Rm
R
R
S
R
S
M
R
S
R
M
S
S
R
S
S
S
R
M
S
S
R
S
S
Pdt
d
L
R
L
R
Pdt
d
L
R
L
R
dt
d
L
R
L
R
u
dt
d
L
R
L
R
u
.
2
..0
.
2
..0
..
..
−++−=
+++−=
+−=
+−=
(3.28)
A quinta equação que se necessita é a equação mecânica do movimento do rotor para o qual
se deve determinar primeiro a expressão do binário electromagnético Tem produzido por motor
assíncrono. Para fazê-lo devem determinar-se as relações da potencia.
A potência de entrada no motor esta dada por:
CCBBAAi iuiuiup ... ++= (3.29)
Agora, tanto para as tensões como para as correntes e concatenações do fluxo aplicam-se
estas relações:
).(.
2
3
).(.
2
3
)(.
2
3
2
xax
xax
xx
C
B
A



ℜ=
ℜ=
ℜ=
(3.30)
Substituindo estas expressões para tensão e corrente em 3.29 obtém-se finalmente:
[ ]...
2
3 *
sSi iup

ℜ= (3.31)
Onde:
ip – Potencia de entrada;
*
Su

– Conjugado do vector da tensão em coordenadas do estactor;
ℜ– Potencia de entrada;
ip – Parte real.
41

63. Estas equações se cumprem para qualquer sistema de coordenadas, mais como o objectivo é
calcular o binário que se exerce sobre o rotor deve trabalhar-se com as equações em coordenadas do
rotor e não em coordenadas do estator como as equações 3.19 e 3.22. Em seguida os passos para
obter as equações em coordenadas do rotor obtêm-se os seguintes resultados:
dt
d
iR
j
dt
d
iRu
R
RR
RR
R
Sr
R
SR
SS
R
S
)(
)(
)(
)(
)()(
.0
...
ϕ
ϕω
ϕ




+=
++=
(3.32)
Se esta expressão é aplicada a cada um dos termos no lado direito da primeira equação 3.32
obtém-se, para o primeiro termo, a energia dissipada em forma de calor, para o segundo a energia
armazenada no campo e para a terceira a energia convertida na forma mecânica, que é a interessa
para determinar o binário electromagnético. Por tanto, pode-se argumentar que a diferencial de
energia convertida na forma mecânica é igual a:
[ ]dtijdW SSRmec .....
2
3 *
ϕω

−ℜ= (3.33)
Supondo-se um deslocamento angular virtual igual a dθ a diferencial da energia mecânica,
também pode ser expressa como:
dtTdTdW rememmec ... ωθ == (3.34)
Combinando as equações 3.33 e 3.34:
[ ]SSem ijT

...
2
3 *
ϕ−ℜ= (3.35)
Decompondo os vetores em seus componentes reais e imaginários:
βα
βα ϕϕϕ
ssS
ssS
ijii
j
.
.*
+=
−=


(3.36)
Então:
( ) [ ]SSssssem iiiT

..
2
3
...
2
3 *
ϕϕϕ αββα ℑ=−= (3.37)
Onde:
ℑ– Parte imaginaria.
Esta expressão deduz-se para uma máquina de 2 polos, portanto se a máquina tiver P polos,
a expressão será:
42

64. [ ] ( )αββα ϕϕϕ ssssSSem ii
P
i
P
T ...
2
.
2
3
..
2
.
2
3 *
−=ℑ=
 (3.38)
Esta equação é aplicável para qualquer sistema de coordenadas. Também é possível
expressa-la com as variáveis em diferentes lados.
A equação mecânica do movimento do motor e do seu mecanismo accionado ou carga
mecânica é:
)(
2
. mmec
m
em T
dt
d
P
JT ω
ω
+= (3.39)
Onde:
Tmec (ωm) – Binário mecânico da carga, que em geral, é a função da velocidade.
Substituindo 38 em 39 obtém-se:
( ) )(
2
....
2
.
2
3
mmec
m
ssss T
dt
d
P
Jii
P
ω
ω
ϕϕ αββα +=− (3.40)
As equações dinâmicas do movimento que constituem finalmente o modelo matemático do
motor (expressas em coordenadas do estator) seriam além da equação 3.40, as equações 3.28. As
expressões das tensões de entrada são:
).(..2
).(cos..2
1
1
tsenUu
tUu
fS
fS
ω
ω
β
α
=
=
(3.41)
Onde:
Uf – Tensão da fase do motor;
ω1 = 2.π.f1 e f1 – Frequência da rede.
3.3. CONSIDERAÇÃO DA VARIAÇÃO DOS PARÂMETROS DO MOTOR
Como foi explicado no capítulo anterior, as barras que compõe a gaiola do rotor dos motores
assíncronos são fabricados para apresentar uma resistência relativamente elevada no arranque e
baixo durante o funcionamento normal. Isto é conseguido acentuando o chamado efeito pelicular
fazendo com que as barras sejam altas e estreitas ou com duas gaiolas de rotor.
Agora, como a gaiola está composta por barra e o anel, nesta ultima resistência praticamente
não varia, pode dizer-se que a resistência do rotor tem uma componente constante, a qual não
depende da frequência do rotor e do escorregamento.
Por outro lado, a relação entre a resistência da corrente alterna e a resistência da corrente
contínua é a seguinte:
43

65. )..2.(..2
.2
.
)..2cos()..2cosh(
)..2()..2(
...
12 fsf
dd
dsendsenh
dRR
o
rccrca
ππω
ρ
µω
α
αα
αα
α
==
=






+
+
=
(3.42)
Onde:
.d – Profundidade da barra.
oµ – Permeabilidade do vácuo
ρ – Resistividade do material da barra que pode ser de cobre ou alumínio
O termo entre parênteses não varia muito com o escorregamento, sendo a variação principal
devido ao factor α. Seguindo este raciocínio, a expressão utilizada para a resistência do rotor será:
sRRsR RVRR .)( 0 += (3.43)
Enquanto à indutância de dispersão do rotor, que também varia de acordo com o
escorregamento que se origina devido à mesma causa, mas tem um efeito contrário, ou seja, no
arranque é menor do que no funcionamento normal, a sua expressão é a seguinte:
s
L
LsL
fv
ffr += 0)( (3.44)
Isto significa que, ao considerar o efeito pelicular na determinação do comportamento
transitório do motor deve- se determinar quatros parâmetros no rotor:
 Dois para a resistência;
 Dois para a indutância de dispersão.
3.4. DETRMINAÇÃO DOS PARAMETROS DO MODELO
Ao usar o modelo matemático do motor de indução, tanto em estado estável ou em regime
permanente como dinâmico ou transitório, é necessário conhecer os parâmetros deste modelo,
fazendo uma identificação dos mesmos. No caso particular de máquinas eléctricas, existem quatro
tipos de métodos para realizar esta identificação:
Métodos clássicos da teoria de controlo: Estes métodos têm conseguido grande
desenvolvimento e são muito precisos, mas exigem instrumentos relativamente complexos e caros.
Métodos baseado em ensaios sem carga: Baseiam-se na realização dos ensaios em vazio,
ensaios em rotor bloqueado e a medição da resistência do estator por fase. Necessitam de uma fonte
de frequência variável.
44

66. Para a aplicação destes métodos é necessário ter fisicamente o motor que não é sempre
possível uma vez que, em alguns casos se encontra instalado e em funcionamento em uma indústria
e não pode ser desinstalado sem a interrupção da produção e em outros casos o motor não foi
comprado e precisamente, a avaliação do seu comportamento através de um modelo é um fator que
pode decidir sobre a compra. Para resolver esse problema, existem métodos que permitem a
determinação dos parâmetros de um motor sem realizar-lhe ensaios. Estes são os seguintes:
Determinação dos parâmetros a partir da aplicação de um método numérico tal como o
dos Elementos Finitos: Para aplicar este método é necessário conhecer todos os dados construtivos
do motor incluindo as características dos aços e outros materiais que compõem o qual, em geral,
torna-se muito difícil.
Método baseado no conhecimento dos dados do catálogo: Este método parte dos dados
apresentados no catalogo do motor, e é menos preciso, mas é muito simples de implementar e
pratico, os erros cometidos raramente invalidam as conclusões que pode ser removido a partir dos
modelos utilizados com base nestes parâmetros como, geralmente são inferiores a 10% e não
superior a 15%. Será usado nesta tese.
Os parâmetros necessários para a solução do modelo são:
 Os que correspondem à resistência e indutância de dispersão (ver as equações 3.43 e
3.44);
 A indutância de dispersão do estator;
 A indutância magnetizante;
 A resistência do estator;
 A inércia e a característica da carga mecânica accionada pelo motor.
Estes parâmetros, que são necessários para a solução dos modelos do motor, não são dados
por nenhum fabricante, salvo raríssimas excepções, contudo, eles são os que determinam os dados
do catálogo do motor que pode ser obtido a partir de qualquer fabricante. Existe uma relação entre
ambos os conjuntos, “o conjunto parâmetros e o conjunto dado do catálogo”, é possível determinar
os primeiros a partir dos últimos. Os dados do catálogo necessário neste caso são:
Potência nominal (Pn) em kW: Expressa a potência mecânica entregue ao mecanismo
accionado ou carga, para qual foi projectado o motor.
Tensão nominal (Un) em Volts: É a tensão aplicada para qual se calcula no motor e deverá
funcionar para trabalhar realmente em condições nominais.
Frequência nominal (fn) em Hz: É a frequência da tensão aplicada para os quais se calculou
no motor e deve operar para trabalhar realmente em condições nominais.
45

67. Corrente nominal (In) em Àmperes: A corrente que flui através do estator do motor quando,
aplicado a tensão nominal da frequência nominal, é carregado pelo mecanismo accionado com a sua
potência nominal.
Velocidade nominal (nn) em r/min: É a velocidade que o motor gira quando, aplicada a
tensão nominal da frequência nominal, esta carregado por um mecanismo accionado com a sua
potência nominal.
Rendimento ou eficiência nominal (ηn) em percentagem: É a relacção, em percentagem,
entre a potência nominal e a potência nominal de entrada, entendida por potência nominal de
entrada, e a potência que toma o motor quando, trabalhando a tensão e a frequência nominais,
entrega potência nominal a carga.
Factor de potência nominal (fpn): É o factor de potência que o motor trabalha em condições
nominais.
Factor de sobrecarga (tmax = Tmax/Tn): É a relação entre o par máximo com a tensão e
frequências nominais e nominais.
Corrente de arranque por unidade ou corrente do rotor bloqueado (ia = irb/In): É a relacção
entre a corrente quando o rotor está bloqueado e o motor tem aplicado a tensão e a frequências
nominais e corrente nominal.
Momento de arranque em por unidade (ta = Tarr/Tn): É a relação entre o torque de arranque
quando se aplica no motor a tensão e as frequências nominais e o momento nominal.
Inércia do motor em kg-m2
(Jm): É o elemento de inércia do rotor do motor. Para calcular os
parâmetros da equação 43 da resistência do rotor deve calcular-se o valor da resistência do rotor em
condições normais de operação RRn = RR (sn) e o valor da resistência do arranque RRk = RR (1).
Para determinar a expressão para a resistência do rotor em funcionamento normal se parte da
expressão que relaciona a energia convertida na forma mecânica em condições nominais Pmec n e a
potência nominal no eixo Pn:
adnmecnnnmec ppPP ++= 1000.. (3.45)
Esta expressão mecnp são as perdas mecânicas nominais e as perdas adicionais nominais.
Acontece que, em condições nominais, estas perdas são muito pequenas e podem ser desprezadas,
podendo-se supor então que a potência nominal de saída é igual à potência convertida para forma
mecânica em condições nominais e de acordo ao explicado anteriormente na dedução da figura 30,
pode se considerar a seguinte igualdade:
n
n
rnrnn
s
s
RIP
−
=
1
...31000. 2
(3.46)
Nesta equação o número 3 é porque o circuito equivalente é por fase do motor e tem três
fases.
46

68. Alem disso, no circuito equivalente (ver capítulo 1), a queda de tensão no ramo fSS XjR .+ ,
em condições nominais é desprezível podendo-se dizer que a tensão aplicada é aproximadamente
igual à tensão entre os pontos a e b. Também no circuito equivalente se cumpre que
n
rn
s
R
é muito
maior do que a reactância de dispersão. Isto faz com que a corrente do rotor Ir esteja praticamente
em fase com a tensão entre os pontos a e b que pode utilizar - se o diagrama fasorial da figura 3.4.
Figura 3.4: Diagrama Fasorial Aproximado ao Circuito Equivalente.
O diagrama fasorial da figura 3.4 pode-se desprezar a corrente nominal do rotor em função
da corrente nominal (que é do estator por suposição) e o factor de potencia nominal )cos( nnfp ϕ= :
)cos(. nnrn II ϕ≈ (3.47)
Substituindo a equação 3.47 e 3.46 e desprezando a resistência do rotor em condições
nominais obtém-se:
2
).).(1.(3
1000..
nnn
nn
rn
fpIs
Ps
R
−
= (3.48)
O escorregamento nominal calcula-se como:
s
ns
n
n
nn
s
−
= (3.49)
Nesta expressão ns é a velocidade síncrona.
P
f
n n
s
.120
= (3.50)
Como se pode verificar a partir da equação 3.48, a resistência do rotor em condições
nominais pode ser calculada a partir da potência nominal, corrente nominal, velocidade nominal e
do factor de potência nominal, “todos dados do catálogo”.
47

69. Para determinar a resistência do rotor a rotor bloqueado, que são as mesmas condições que
no arranque, se parte da expressão do torque ou binário electromagnético:
s
R
IT r
r
s
em ..
3 2
ω
= (3.51)
Nesta expressão ωs é a velocidade síncrona em radianos por segundo que é igual a:
ss n.
60
.2 π
ω = (3.52)
O binário electromagnético pode ser considerado aproximadamente igual binário mecânico
da carga, desprezando as perdas mecânicas como já foi feito anteriormente. Então pode-se
considerar a seguinte expressão para o binário nominal:
n
rn
rn
s
n
s
R
IT ..
3 2
ω
= (3.53)
E para o binário de arranque (lembre-se que o deslocamento durante o arranque é igual a 1
(um) teremos que:
rkrarr
s
arr RIT ..
3 2
.
ω
= (3.54)
Nesta expressão Iarr.r é a corrente de arranque.
Dividindo a equação 3.54 por 3.53 obtém-se:
n
rn
rk
rn
rarr
n
arr
s
R
R
I
I
T
T
..
2
.






= (3.55)
O termo à esquerda é o binário de arranque por unidade (dado do catálogo). Uma vez que,
durante o arranque a corrente de magnetização é muito baixa em comparação com as do estator e do
rotor, é possível fazer a seguinte aproximação:
n
rn
rk
aa s
R
R
it ..2
= (3.56)
A partir desta equação, isola-se a resistência do rotor durante o arranque ou a rotor
bloqueado:
na
a
rnrk
si
t
RR
.
. 2
= (3.57)
Como se pode ver, uma vez calculada a resistência do rotor em condições nominais é
possível determinar com este valor:
 A velocidade nominal;
48

70.  A corrente de arranque em por unidade e o binário de arranque em por unidade;
 A resistência de rotor a rotor bloqueado ou no arranque.
Como no momento de arranque o escorregamento é igual a 1 e em condições normais de
operação é igual ao escorregamento nominal sn, a partir da equação 3.43 podem surgir, as duas
equações seguintes que têm duas incógnitas; 0RR e RVR :
RVRrk
nRVRrn
RRR
sRRR
+=
+=
0
0 .
(3.58)
Resolvendo estas equações teremos:
n
rknrn
R
s
RsR
R
−
−
=
1
.
0 (3.59)
n
rnrk
RV
s
RR
R
−
−
=
1
(3.60)
Quando há acoplamento magnético entre duas bobinas, a maior parte do fluxo magnético
produzido pela corrente em uma concatena passa também para o outro, bem há uma parte que não
atinge o outro enrolamento, é o denominado Fluxo de Dispersão. As concatenações do fluxo por
unidade de corrente deste fluxo dão lugar a indutância de dispersão. Como as máquinas eléctricas
de indução trabalham com corrente alterna, o parâmetro que avalia o efeito indutivo é, neste caso, a
reactância cuja relação com a indutância está dada pela expressão:
LfX ..2 ⋅⋅= π (3.61)
Como existe um fluxo de dispersão tanto no estator como no rotor, existe uma reatância de
dispersão (e uma indutância de dispersão) no estator e uma no rotor que são as que aparecem nos
circuitos equivalentes do capitulo 1 com as denominações Xd1 e Xd2
’
.
Devido o acoplamento magnético apertado entre o estator e o rotor, é muito difícil separar
mediante ensaios ou os cálculos estes dois parâmetros e normalmente trabalha com a denominada
Reactância de Dispersão Total Xcc.
21 ddcc XXX ′+= (3.62)
Nos motores de uso geral geralmente supõem-se que 40% da reactância corresponde ao do
estator e 60% do rotor.
O feito pelicular da mesma forma que afecta a resistência, afecta também a reactância mais
em sentido contrário, ou seja, maior frequência menor reactância e vice-versa. Portanto, no arranque
a reactância de dispersão do rotor é pequena e o funcionamento normal é maior. Para diminuir o
erro que isto implica, se considerará de forma conjunta a variação da reactância do estator e do rotor
49

71. embora se sabe que está vária muito mais e posteriormente se separam com o critério de 40% e
60%.
Seguindo o critério da equação 3.44 pode-se considerar que:
s
X
XX dv
dcc += 0 (3.63)
Para encontrar a reatância de dispersão total se utilizará a expressão 3.23 do Capitulo 1 que
será escrita da seguinte forma:
ccS
fn
X
U
T
..2
.3 2
max
ω
≈ (3.64)
O binário máximo calcula-se a partir do factor de sobrecarga tmax como:
nTtT .maxmax = (3.65)
E o binário nominal calcula-se partir da seguinte fórmula:






=
30
.
1000.
π
n
n
n
n
P
T
(3.66)
Combinando estas três equações obtém-se a reatância de dispersão em condições normais.
A partir do valor da reatância de dispersão total em condições nominais, reduz-se a reatância
de dispersão do estator, que se considera constante, e a reatância de dispersão do rotor avaliada
neste caso para o escorregamento que corresponde ao binário máximo sm:
ccmd
ccd
mddcc
XsX
XX
sXXX
.6,0)(
.4,0
)(
2
1
21
=′
=
′+=
(3.67)
Com as reactâncias calculam-se as indutâncias:
n
md
fr
n
d
fs
f
sX
L
f
X
L
..2
)(
..2
2
1
π
π
′
=
=
(3.68)
Para calcular o escorregamento que corresponde o binário máximo, utiliza-se a equação 3.25
do capitulo1 (fórmula de Kloss), considerando que a = 1 e substituindo o escorregamento por seu
valor nominal sn obtém-se:
50

72. )1.(2
.2
max
max
m
m
n
m
m
n
n s
s
s
s
s
s
T
T
t
+
++
==
(3.67)
Isolando o escorregamento para o binário máximo teremos:
( )
nn
nn
nm
sts
ststt
ss
..2.21
..2.21
.
max
max
2
maxmax
−+
−+−+
= (3.68)
Figura 3.5: Circuito Equivalente do Motor no Arranque.
Para calcular a reatância no arranque Xcc.arr = Xd1 +X
´
d2k se fará referencia ao circuito
equivalente aproximado do motor no arranque que é apresentada na figura 3.5. Como pode ser
visto, despreza-se a corrente em vazio por ser muito menor que a corrente de arranque, que é então
igual a corrente do rotor. De acordo com este circuito, a corrente de arranque é dada por:
( )2
.
2
)( arrccrkS
fn
arr
XRR
U
I
++
= (3.69)
A equação 3.69 pode ser efectuada por unidade da seguinte forma:
2
.
22
.
2
1
)(.
1






+




 +
=
++
=
b
arrcc
b
rkS
arrccrkSn
n
arr
Z
X
Z
RRXRRII
I
(3.70)
Nesta expressão
n
nf
b
I
U
Z = é a impedância base, igual à relação entre a tensão de fase e a
corrente de fase nominal, igual à de linha se supõem que o motor esta ligado em estrela (se não está
pode ser assumida uma estrela equivalente), então:
( ) ( ) 2
.
2
1
puarrccpurkS
a
XRR
i
++
= (3.71)
Nesta expressão isola-se a reatância de dispersão total em por unidade de arranque:
51

73. ( )( )2
2
.
1
purkS
a
arrpucc RR
i
X +−





= (3.72)
Nesta expressão aparece a resistência do estator a qual se explicará posteriormente como se
calcula.
Multiplicando pela impedância base obtém-se o valor absoluto:
bpuarrccarrcc ZXX .... = (3.73)
Ora eliminando a reactância de dispersão do rotor no arranque
1.
'
2 darrcckd XXX −= (3.74)
E o valor de indutância de dispersão seria:
n
dkd
frk
f
X
f
X
L
..2
)1(
..2
'
2
'
2
ππ
== (3.75)
Com esta informação pode-se calcular os coeficientes da equação 3.44 simultaneando as
equações com duas incógnitas:
( )
m
frkfrm
fV
m
frmfrk
f
s
LLs
L
s
LsL
L
−
−
=
−
−
=
1
.
1
.
0
(3.76)
Em seguida vai se calcular o valor da indutância magnetizante ou mutua LM na qual se
calcula determinando primeiro a reatância magnetizante XM com referência ao circuito equivalente
do Capítulo 1, que é repetido na figura 3.6.
Figura 3.6: Circuito Equivalente do Motor no Assíncrono.
Seguidamente passa-se a calcular o valor da reatância magnetizante Xm é a que corresponde
ao fluxo mútuo, por ela circula a corrente magnetizante Im como se pode verificar no circuito
equivalente da figura 1.6. Observando este mesmo circuito equivalente e considerando a resistência
52

74. de perdas de aço é muito maior do que a reatância e, portanto vai ser desprezada, conclui-se que a
sua expressão é:
m
abn
m
I
U
X = (3.77)
Onde:
abnU
– Tensão entre os pontos a e b do circuito em condições nominais.
Para calcular esta tensão deve - se basear na seguinte equação fasorial:
)..( 1dSnnfabn XjRIUU +−= (3.78)
A equação fasorial 78 corresponde ao diagrama fasorial da figura 3.7.
Figura 3.7: Diagrama de Fase que Corresponde a Equação 78.
Neste diagrama fasorial verifica-se que:
2
2
1....
1..)(..
..)cos(..
nnSnnSnabn
nnSnnS
nnSnnS
abn
n
fpIXfpIRUU
fpIXsenIXBC
fpIRIRAB
UODOA
UOC
−−−≈
−=≈
=≈
=≈
=
ϕ
ϕ
(3.79)
A corrente magnetizante em condições nominais Im pode ser calculada a partir da
figura 3.4.
22
rnnm III −= (3.80)
Quando se trabalha a tensão e frequência constante ou com frequência variável, mas com
uma lei de controlo que mantém o fluxo constante, esta reactância pode assumir-se constante.
Para o cálculo da resistência do estator se determinará primeiro as perdas de cobre no estator
a partir de um balanço de potência no motor usando a seguinte expressão:
53

75. ∑ +++−= )( adnmecnacncobrncobsn pppppérdidasnp (3.81)
Onde:
cobsnp – Perdas de cobre nominais no estator;
cobrnp – Perdas de cobre nominais no rotor;
acnp – Perdas de aço nominais;
mecnp – Perdas mecânicas nominais;
adnp – Perdas adicionais ou indeterminadas nominais;
∑pérdidasn – Soma de todas as perdas existentes no motor em condições
nominais, que são calculadas a partir da seguinte expressão:
inn
n
n
P
P
perdasn −=∑ 100/
1000.
η
(3.82)
Onde:
Pinn – Potencia nominal de entrada dada por:
nnninn fpIUP ..3= (3.83)
As perdas de cobre nominais no rotor são calculadas a partir da seguinte expressão:
rnrncobrn RIp ..3 2
= (3.84)
As perdas de aço nominais estão entre 15% e 20% do somatório total do quadrado das
perdas, supõem-se 20% para motores menores de 15 kW e 17% para motores entre 15 e 100 kW e
15% para motores maiores de 100 kW.
As perdas mecânicas nominais são sempre menores que as de aço, por isso devem ser
considerados sempre ¾ do aço.
As perdas adicionais determinam-se seguindo as normas da IEEE, ou seja, se consideram
1,8% da potencia nominal para motores menores de 90 kW, 1,5% para motores entre 90 e 375 kW,
1,2% para motores entre 375 kW e 1850 kW e 0,9% para motores maiores.
Uma vez obtidas as perdas de cobre nominais no estator, a resistência do estator calcula-se
pela seguinte expressão:
2
.3 n
cobsn
S
I
p
R = (3.85)
3.5. EQUAÇÕES EM POR UNIDADE
54

76. Como é bem conhecida, a expressão das equações das máquinas e sistemas eléctricos de
potencia em por unidade facilita notavelmente a sua escrita e avaliação dos resultados obtidos por
meio dos modelos de simulação. Nesta sessão, vamos tratar da abordagem em por unidade das
equações da máquina assíncrona. A primeira coisa a ser feita, é seleccionar os valores de base dos
diferentes parâmetros e variáveis.
Começa-se com a selecção dos seguintes valores base e o restante é deduzido a partir destas
relações:
 Tensão Base nb UU .2=
 Corrente Base nb II .2=
 Impedância base
b
b
b
I
U
Z =
 Potencia Base
3
.2..2.. n
nnbbb
S
IUIUP ===
 Velocidade base
P
Sb
2
1ωωω ==
 Fluxo Base
111 2
.2.2
f
UUU nnb
b
πωω
ϕ ===
 Tempo em pu em radianos t
P
t S .
2
..1 ωωτ ==
Estes valores de base podem aplicar-se directamente às equações eléctricas 3.28, no entanto,
é necessário definir os valores base de quantidades mecânicas tais como o binário base e a inércia
base que deve ser compatível com as anteriores, devido ao carácter electromecânico das máquinas
eléctricas rotativas.
A equação 3.40 pode ser definida também da seguinte forma:
2
.....
2
....
2
.
2
3 P
d
d
JTI
P
U
I
i
I
iP
SS
S
m
mecb
S
b
b
s
b
s
b
s
b
s
ωω
τ
ω
ω
ωϕ
ϕ
ϕ
ϕ βββα
+=





−
(3.86)
( )
2
......
2
.
P
d
d
JT
s
ii S
mpu
mec
S
n
puspuspuspus ω
τ
ω
ω
ϕϕ αββα +=− (3.87)
Então o binário base é:
S
n
b
s
T
ω
=
55

77. E a inércia base é:
2
.
2 P
s
J
S
n
b
ω
=
A equação do movimento em por unidade é:
( )
τ
ω
ϕϕ αββα
d
d
JTii
mpu
pumecpupuspuspuspus .... +=−
CAPÍTULO IV
ANÁLISE DE UM ESTUDO DE CASO
4.1. DESCRIÇÃO DO CASO DO ESTUDO
Neste caso de estudo, analisaram-se os processo de arranque e paragem de um motor
assíncrono que move uma instalação hidráulica, conforme ilustrado na figura 4.1, cuja característica
de altura manométrica ou carga hidráulica em função do fluxo ou caudal da água é apresentada na
figura 37. O caudal ou fluxo da água deve ser regulado a partir de 18 m3
/h até 25 m3
/h.
Figura 4.1: Sistema Hidráulico Estudado.
56

78. 0 5 10 15 20 25 30 35 40 45
50
55
60
65
70
Fluxo em m3/h
Alturamanométricaemm
Caracteristica da instalação hidraulica
Figura 4.2: Característica Da Instalação Hidráulica.
A bomba apropriada para esta instalação é a do tipo LHK da Alfa Laval de velocidade
nominal 2930 rpm. Este fabricante constrói três tipos de bombas desta categoria cujas
características são a presentadas na figura 4.3. Dadas as características e as exigências da instalação,
verificou-se que a LHK 112 é a mais adequada. A inércia do rotor da bomba é de 0,2 kg-m2
. Para
encontrar o ponto de funcionamento da bomba com o fluxo máximo, ou seja, com a válvula de
saída completamente aberta, se forem simultâneas as características das figuras 4.1 e 4.2.
Figura 4.3: Características das Bombas LHK da Alfa Laval
Conforme é mostrado na figura 4.3, o ponto de funcionamento da bomba corresponde a um
caudal Q = 25,4 m3
e uma altura manométrica H = 58,6 m.
Esta bomba conta com o motor assíncrono, cujos dados são apresentados na Tabela 4.1.
Tabela 4.1: Dados do Catalogo do Motor
Marca Siemens
Tensão em V 400
57

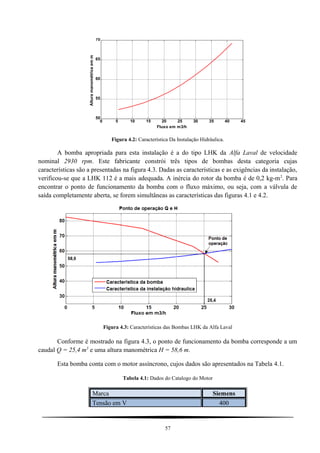
79. Potência em kW 18,5
Velocidade em rpm 2935
Corrente em A 33
Rendimento nominal em % 91,5
Factor de potência 0,89
Iarr/In 8,2
Tarr/Tn 2,6
Tmax/Tn 3,3
Inércia do motor em kg-m2
0,054
Inércia da carga em kg-m2
0,2
Seguindo o algoritmo explicado no capítulo anterior calcularam-se os valores bases e os
parâmetros do motor assíncrono com os resultados dos valores mostrados na tabela 4.2 e os valores
dos parâmetros na tabela 4.3.
Tabela 4.2: Valores Base
Tensão de base em V 326,6
Corrente base em A 46,67
Velocidade base em rpm 3000
Impedância base em ohms 7
Binário base em N-m 72,58
Inércia base em kg-m2
7,31.10-4
Tabela 4.3: Parâmetros do Motor Assíncrono
Parâmetro Valor Absoluto Por Unidade
Constantes da resistência do rotor RR0 e RRV em
ohms
[0,1369 0,1457] [0,0196 0,0208]
Inductância de dispersão do estator LfS em mH 1,3 0,0582
Constantes da inductância de dispersão do rotor
Lf0y LfV em mH
[0,876 1] [0,0391 0,0462]
Inductância magnetizante Lm em mH 46,7 2,0934
Resistência do estator RS em ohms 0,155 0,022
Inércia total en kg-m2
0,1240 169,52
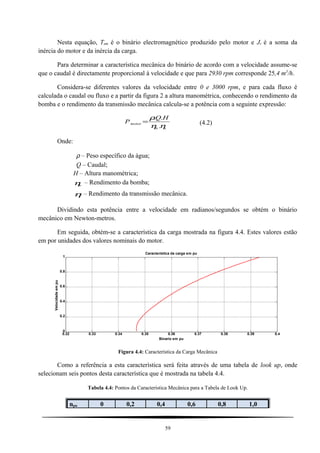
4.2. CARACTERÍSTICAS DA CARGA MECÁNICA
As características do processo do arranque da moto bomba dependem do binário mecânico
resistivo Tmec que a bomba impõe ao motor, que é diferente para cada valor de velocidade rω . Isto
é porque a equação mecânica fundamental que descreve este processo é a seguinte:
dt
d
JTT r
trmecem
ω
ω .)( += (4.1)
58

80. Nesta equação, Tem é o binário electromagnético produzido pelo motor e Jt é a soma da
inércia do motor e da inércia da carga.
Para determinar a característica mecânica do binário de acordo com a velocidade assume-se
que o caudal é directamente proporcional à velocidade e que para 2930 rpm corresponde 25,4 m3
/h.
Considera-se diferentes valores da velocidade entre 0 e 3000 rpm, e para cada fluxo é
calculada o caudal ou fluxo e a partir da figura 2 a altura manométrica, conhecendo o rendimento da
bomba e o rendimento da transmissão mecânica calcula-se a potência com a seguinte expressão:
tb
motor
HQ
P
ηη
ρ
.
..
= (4.2)
Onde:
ρ – Peso específico da água;
Q – Caudal;
H – Altura manométrica;
bη – Rendimento da bomba;
tη – Rendimento da transmissão mecânica.
Dividindo esta potência entre a velocidade em radianos/segundos se obtém o binário
mecânico em Newton-metros.
Em seguida, obtém-se a característica da carga mostrada na figura 4.4. Estes valores estão
em por unidades dos valores nominais do motor.
0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.4
0
0.2
0.4
0.6
0.8
1
Binario em pu
Velocidadeempu
Caracteristica da carga em pu
Figura 4.4: Característica da Carga Mecânica
Como a referência a esta característica será feita através de uma tabela de look up, onde
selecionam seis pontos desta característica que é mostrada na tabela 4.4.
Tabela 4.4: Pontos da Característica Mecânica para a Tabela de Look Up.
npu 0 0,2 0,4 0,6 0,8 1,0
59

81. Tpu 0,344 0,3488 0,3556 0,3647 0,3772 0,3934
4.3. MODELO EM SIMULINK PARA A ANÁLISES DOS PROCESOS DE ARRANQUE E
PARAGEM
Figura 4.5: Modelo Geral em SIMULINK para o Estudo dos Processos de Arranque e Paragem
A figura 4.5 mostra o padrão geral, utilizadas para estudo dos processos de arranque e
paragem do motor assíncrono. Compreende, como se mostra, de quatro módulos:
 A Máquina Assíncrona que é um modelo onde são resolvidas as equações dinâmicas
eléctricas do motor que tem como entradas as componentes de tensão nos eixos de
referência do estator (usx e usy) e o rotor (urx e ury considerados zero porque se trabalha
com um motor com rotor em curto circuito), a frequência angular ω = 2.π.f1 e a
velocidade do rotor ωm e tem como saídas os valores instantâneos das correntes do
estator e rotor (cas e car) e o valor efectivo da corrente do estator (corr1).
 A Carga Mecânica onde se resolve a equação dinâmica mecânica do motor tem como
entrada o binário e como a saída a velocidade ωr.
60

82.  O selector de alimentação que é o bloco onde, mediante o número que aparece na
entrada, seleciona o tipo de arranque e paragem que se deseja analisar. As saídas deste
bloco são as componentes da tensão do estator e a frequência angular.
 O Bloque de Medições onde se pode medir e armazenar as leituras das principais
variáveis.
4.3.1. Máquina Assíncrona
4
corr1
3
par
2
Iralfa
1
Isalfa
s rr
rr
w 1-w m
Idr
Iqr
Iralfa
ejsitak1
w 1
Ids
Iqs
Isalfa
ejsitak
i1 o1
dcero
Terminator
Scope1
Scope
sqrt
Math
Function2
u2
Math
Function1
u2
Math
Function
Lm
s
delta
Ls
Lr
Inductancias
rs
-K-
1/s
Fiqs
1/s
Fiqr
1/s
Fids
1/s
Fidr
delta
Lm
Ls
Lr
fids
fiqs
fidr
fiqr
ids
iqs
idr
iqr
Corrientes
Lmu
6
wm
5
ury
4
urx
3
usy
2
usx
1
w1
Figura 4.6: Modelo da Máquina Assíncrona
A figura 4.6 mostra o modelo em SIMULINK da máquina assíncrona, onde as equações
3.28 do Capítulo 3 são resolvidas tendo em conta a variação da resistência e da reatância de
dispersão do rotor com o escorregamento. Existe uma janela onde se perguntam a resistência do
estator, a indutância de dispersão do estator, a indutância magnetizante e as constantes que
permitem calcular a resistência e a indutância do rotor em função do escorregamento. Todos estes
valores são dados em por unidade.
4.3.2. Carga Mecânica
A figura 4.7 mostra o modelo da carga mecânica, onde se resolve a equação dinâmica fundamental
do motor tendo em conta a características tendo em conta a característica mecânica na qual se
apresenta na forma de tabela de Look Up. Deve-se introduzir-se também a inercia total, ou seja a
soma da inercia do motor e a inercia da carga, neste caso, a bomba. Estes valores também estão em
por unidade.
61

83. Figura 4.7: Modelo da Carga Mecênica
4.3.3. Selector de Alimentação
Figura 4.8: Selector de Alimentação
A figura 4.8 mostra o selector que permite selecionar o tipo de análise transitório que se
deseja obter. Utiliza-se uma ferramenta de SIMULINK que permite seleccionar uma entrada de 8
possibilidades, colocando na entrada do bloco o número correspondente. Por exemplo se
colocarmos o número zero, aparece na saída a entrada da tensão correspondente ao arranque direto,
se colocarmos o número 1 aparece a entrada correspondente ao arranque a tensão reduzida. As 8
possibilidades aparecem descritas na tabela 4.5.
Tabla 4.5: Possibilidades do Selector de Alimentação
Número Tipo de Alimentação
0 Arranque directo à rede
1 Arranque a tensão reduzida
62

84. 2 Arranque suave em rampa com soft starter
3 Arranque suave em S com soft starter
4 Arranque com paragem dinámica
5 Arranque com inversão
6 Arranque a frequência variável em rampa
7 Arranque a frequência variável em S
Para cada caso, aparece uma janela onde são pedidos os parâmetros de ajuste que
caracterizam o fenômeno estudado.
4.3.4. Medições
Figura 4.9: Bloco de Medições
Na figura 4.9 mostra-se o bloco de medições, onde são recolhidos os dados para fazer os
gráficos de velocidade, corrente e binário em função do tempo e da velocidade em função do
binário nos diferentes processos dinâmicos.
Como o modelo da máquina está resolvido em por unidade, este bloco tem uma janela que
pede os valores básicos de cada variável para dar os resultados em valores com unidade.
Para ilustrar estas variáveis se emprega um programa em MATLAB denominado ploteo
dinamica que aparece abaixo:
%PROGRAMA DE PLOTEO DE VARIABLES
 Figura (1):plot (tempo,velocidade,'r');grid
63

85.  figura (2):plot (tempo,corrente,'r');grid
 figura (3):plot (tempo,binário,'r');grid
 figura (4):plot (binário,velocidade,'b');grid
4.4. ANALISES DOS PROCESSOS DE ARRANQUE
A seguir analisa-se, para cada tipo de arranque, a variação da velocidade, o binário e a
corrente em função do tempo e a característica mecânica dinâmica, ou seja, velocidade em função
do binário no processo de arranque.
Nos arranques em que não são directo a rede são supostos ajustes dos parâmetros de
arranque que dão lugar aos menores picos da corrente e do binário.
4.4.1. Arranque directo da rede.
0 0.1 0.2 0.3 0.4 0.5 0.6
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.10: Velocidade em Função do Tempo no Arranque Directo à Rede.
64

86. 0 0.1 0.2 0.3 0.4 0.5 0.6
0
50
100
150
200
250
300
350
400
Tempo em segundos
CorrenteemA
Figura 4.11: Corrente em Função do Tempo no Arranque Directo à Rede
0 0.1 0.2 0.3 0.4 0.5 0.6
-200
-100
0
100
200
300
400
500
600
700
Tempo em segundos
BinarioemN-m
Figura 4.12: Binário em Função do Tempo no Arranque Directo à Rede
65

87. -200 -100 0 100 200 300 400 500 600 700
0
500
1000
1500
2000
2500
3000
Binario em N-m
Velocidadeemrpm
Figura 4.13: Característica Mecânica Dinâmica no Arranque Directo à Rede.
4.4.2. Arranque a Tensão Reduzida (Y-∆)
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.14: Velocidade em Função do Tempo no Arranque a Tensão Reduzida
66

88. 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
0
50
100
150
200
250
Tempo em segundos
CorrenteemA
Figura 4.15: Corrente em Função do Tempo no Arranque a Tensão Reduzida
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
-100
-50
0
50
100
150
200
250
300
Tempo em segundos
BinarioemN-m
Figura 4.16: Binário em Função do Tempo no Arranque a Tensão reduzida
-200 -100 0 100 200 300 400 500 600 700 800
0
500
1000
1500
2000
2500
3000
Binario em N-m
Velocidadeemrpm
Figura 4.17: Característica Mecânica dinâmica no Arranque a Tensão Reduzida
4.4.3. Arranque Suave na Rampa
67

89. 0 0.5 1 1.5 2 2.5 3
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.18: Velocidade em Função do Tempo no Arranque Suave na Rampa
0 0.5 1 1.5 2 2.5 3
0
20
40
60
80
100
120
140
160
180
200
Tempo em segundos
CorrenteemA
Figura 4.19: Corrente em Função do Tempo no Arranque Suave na Rampa
0 0.5 1 1.5 2 2.5 3
-20
0
20
40
60
80
100
120
140
Tempo em segundos
BinarioemN-m
Figura 4.20: Binário em Função do Tempo no Arranque Suave na Rampa
68

90. -200 -100 0 100 200 300 400 500 600 700 800
0
500
1000
1500
2000
2500
3000
Binario em N-m
Velocidadeemrpm
Figura 4.21: Característica Mecânica Dinâmica no Arranque Suave na Rampa
4.4.4. Arranque Suave em S
0 1 2 3 4 5 6 7 8 9
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.22: Velocidade em Função do Tempo no Arranque Suave Em S
0 1 2 3 4 5 6 7 8 9
0
50
100
150
200
Tempo em segundos
CorrenteemA
Figura 4.23: Corrente em Função do Tempo no Arranque Suave em S
69

91. 0 1 2 3 4 5 6 7 8 9
0
20
40
60
80
100
120
140
Tempo em segundos
BinárioemN-m
Figura 4.24: Binário em Função do Tempo no Arranque Suave em S
-200 -100 0 100 200 300 400 500 600 700 800
0
500
1000
1500
2000
2500
3000
Binário em N-m
Velocidadeemrpm
Figura 4.25: Característica Mecânica Dinâmica no Arranque Suave em S
4.4.5. Arranque a Frequência Variável na Rampa
70

92. 0 1 2 3 4 5 6 7 8 9
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.26: Velocidade em Função do Tempo no Arranque a Frequência Variável na Rampa
0 1 2 3 4 5 6 7 8 9
0
10
20
30
40
50
60
Tempo em segundos
CorrenteemA
Figura 4.27: Corrente em Função do Tempo no Arranque a Frequência Variável na Rampa
0 1 2 3 4 5 6 7 8 9
0
10
20
30
40
50
60
70
80
Tempo em segundos
BinárioemN-m
Figura 4.28: Binário em Função do Tempo no Arranque a Frequência Variável na Rampa.
71

93. -200 -100 0 100 200 300 400 500 600 700 800
0
500
1000
1500
2000
2500
3000
Binário em N-m
Velocidadeemrpm
Figura 4.29: Característica Mecânica Dinâmica no Arranque a Frequência Variável na rampa
4.4.6. Arranque com frequência variável em S
0 1 2 3 4 5 6 7 8 9
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.30: Velocidade em Função do Tempo no Arranque a Frequência Variável em S
0 1 2 3 4 5 6 7 8 9
0
5
10
15
20
25
30
35
40
45
Tempo em segundos
CorenteemA
72

94. Figura 4.31: Corrente em Função do Tempo no Arranque a Frequência Variável em S
0 1 2 3 4 5 6 7 8 9
0
10
20
30
40
50
60
70
Tempo em segundos
BinárioemN-m
Figura 4.32: Binário em Função do Tempo no Arranque a Frequência Variável em S
-200 -100 0 100 200 300 400 500 600 700 800
0
500
1000
1500
2000
2500
3000
Binário em N-m
Velocidadeemrpm
Figura 4.33: Característica mecânica Dinâmica no Arranque a Frequência Variável em S
73

95. 4.5. COMPARAÇÃO ENTRE OS DIFERENTES TIPOS DE ARRANQUE
Tabela 4.6: Comparação de Arranques
Tipo de
Arranque
Pico de
Corrente (A)
Pico de
Binário (N-m)
Tempo de
Arranque (s)
Oscilações do
Binário
Directo a rede 350 680 0,5
Muito grande e
mantida
Tensão reduzida
(Y-∆)
210 250 1,4
Grandes com
menos picos
Suave na rampa
(Soft starter)
162 118 2
Pequenas e
rápidas
Suave em S
(Soft starter)
158 108 6 nenhum
Freq. variável na
rampa
56 75 3,2
praticamente
nenhum
Freq. variável
em S
40 68 4
praticamente
nenhum
Na tabela acima se mostra uma comparação entre os parâmetros mais importantes que
avaliam a qualidade de cada tipo de arranque.
Pode ser visto que o arranque directo a rede apresenta grandes picos de corrente e de binário
oscilações muito grandes e mantida embora seja mais rápido. É admissível se o motor arranca
poucas vezes ao dia e a rede que lhe alimenta suporta a queda de tensão que provoca esta alta
corrente.
O arranque a tensão reduzida melhora um pouco a situação já que tem menos picos de
corrente e binário e menos oscilações.
Os arranques suaves tanto na rampa como em S são notavelmente superiores apesar de ter
um arranque um pouco mais lento. Observam-se picos de correntes e binários bastante mais baixos
e praticamente sem oscilações. O arranque é mais lento.
É evidente que os arranques a frequência variável são os de mais qualidade principalmente
por baixos picos da corrente e binário e poucas oscilações.
Os eixos das coordenadas da característica mecânica dinâmica serão mantidos iguais em
todos os casos, com o objectivo de realizar uma comparação entre eles. A forma desta característica
dá uma ideia da suavidade do arranque. A característica ideal seria uma recta do binário constante
até perto da velocidade estável, que deve diminuir para coincidir com o binário da carga.
Observa-se como o arranque directo a rede provoca grandes picos do binário e oscilações
violentas que trazem como consequências vibrações no rotor que podem afectar a integridade dos
rolamentos. Os arranques suaves e a frequência variável se caracterizam pela ausência de oscilações
apreciáveis. Os arranques suaves e a frequência variável são caracterizados pela ausência de
oscilações, que contribui para aumentar à vida útil do motor e praticamente não afecta a rede
eléctrica.
74

96. 4.6. PARAGEM DO MOTOR ASSINCRONO
Com este mesmo motor serão analisados dois tipos de paragens:
 Paragem dinâmica;
 Paragem por inversão ou contra corrente.
No caso de paragem dinâmica se supõe que a alimentação da corrente contínua é eliminada a
poco tempo de parar o rotor e no caso de paragem por inversão que, mediante alguns meios, o
motor desliga-se quando se atinge a velocidade zero.
4.6.1. Paragem dinâmica.
0.8 0.9 1 1.1 1.2 1.3
-500
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.34: Variação da Velocidade na Paragem Dinâmica
0.8 0.9 1 1.1 1.2 1.3
0
200
400
600
800
1000
Tempo em segundos
CorrenteemA
Figura 4.35: Variação da Corrente na Paragem Dinâmica
75

97. 0.8 0.9 1 1.1 1.2 1.3
-4000
-3000
-2000
-1000
0
1000
Tempo em segundos
BinárioemN-m
Figura 4.36: Variação do Binário na Paragem dinâmica
Note-se que, como resultado da aplicação da corrente contínua ao desligar o motor a
velocidade torna-se zero muito rapidamente, em menos de 100 m/s. Isto deve-se ao pico de binário
negativo de mais de 3000 N-m. A fonte da corrente contínua pode desconectar-se após 100
milissegundos.
4.6.2. Paragem por Inversão
0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2 1.25
0
500
1000
1500
2000
2500
3000
Tempo em segundos
Velocidadeemrpm
Figura 4.37: Variação da Velocidade na Paragem por Inversão
76

98. 0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2
0
200
400
600
800
1000
Tempo en segundos
CorrenteemA
Figura 4.38: Variação da Corrente na Paragem por Inversão
0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2
-2500
-2000
-1500
-1000
-500
0
500
Tempo em segundos
BinárioemN-m
Figura 4.39: Variação do Binário d Paragem por Inversão
Como pode ver-se, a paragem por inversão os picos da corrente e do binário são também
muito grandes e produzem mais oscilações que na paragem dinâmica para o qual os rolamentos são
mais afectados. Além disso, é necessário um dispositivo que desconecta o motor para alcançar a
velocidade zero.
77

99. CONCLUSÕES
De acordo com os resultados obtidos no presente documento pode de se chegar às seguintes
conclusões:
 O motor assíncrono trifásico de rotor de gaiola no arranque directo a rede consume uma
corrente elevada entre 5 e 9 vezes a sua corrente nominal. Este valor elevado desaparece
rapidamente ao arrancar o motor.
 Devido a sua robustez, se o arranque não se produzir com uma frequência, estes valores
elevados não causam danos ao motor ou redução de sua vida útil.
 Se, no entanto, se provocar quedas de tensão na rede eléctrica das quais fazem parte,
podem dar lugar a fenómenos prejudiciais para outras cargas ligadas à mesma rede, obrigando a
diminuir essas correntes e causar oscilações no mecanismo accionado que dão origem a vibrações
que podem ser prejudiciais.
 Existem diferentes métodos para reduzir esta corrente de arranque, a maioria das quais
são baseadas na diminuição da tensão, mantendo a frequência constante.
 Esta redução de tensão da frequência constante provoca uma diminuição significativa no
binário de arranque, que faz com que ele não seja adequado para cargas que exigem um elevado
binário de arranque, adaptando-se muito bem às cargas de velocidade como bombas, compressores
e ventiladores centrífugos.
 Apenas a utilização de variadores de velocidade que controlam simultaneamente a tensão
e a frequência permite arrancar qualquer tipo de carga sem diminuir o binário de arranque. No
entanto, sua utilização para o arranque não é justificável economicamente, quase em nenhum dos
casos.
 Em geral, existem dois métodos gerais de variação da tensão para controlar o arranque:
variação discreta usando autotransformadores ou arrancador estrela-triângulo e método de arranque
suave denominados Soft starters
 O método de arranque suave é tecnicamente superior aos outros métodos, pois permite
um controlo suave da corrente e o binário sem sujeitar o mecânismo accionado a perigosas
oscilações que podem danificar o seu rolamento.
 Embora esse método seja o mais caro, o arranque suave é justificada por diversas vezes já
que a larga vida útil do mecanismo accionado e reduz os distúrbios na rede incorporando outras
funções como são a paragem e a proteccção do motor.
 Embora tecnicamente o melhor método, não é rentável utilizar um variador de velocidade
apenas para arrancar e parar, porque é mais caro do que o arrancador suave e este funciona de modo
satisfatório a melhorar a qualidade do processo de arranque.
 Quanto aos métodos de paragem, se quisermos parar o motor suavemente o método de
diminuição na rampa da velocidade é o melhor. Para paragem de emergência ou uma paragem
muito rápida o método de paragem dinâmica com a introdução da corrente contínua no estator é o
mais apropriado.
78

100. RECOMENDAÇÃO
Recomenda-se continuar a investigação sobre os métodos de arranque e paragem aplicados a
outros tipos de mecanismos como as esteiras ou como os elevadores.
BIBLIOGRAFIA
79

101.  FEITO, Javier Sainz. Máquinas Eléctricas – Editora Prentice Hall, 2000
 FITZGERALD, A. E; KINGSLEY JUNIOR, C.; KUSKO, A. Máquinas Eléctricas
Brasil: McGraw-Hill do Brasil,
 MONTIEL, Angel Costa. Variadores de Velocidad de Motores de Inducción por
Variación de la Frecuencia – Monografía, Habana, Cuba, 2000
 RASHID, Muhammad H. Electrónica de Potência – São Paulo: Makron Books, 1997.
 WEG, Manuais de instalação de soft-starters Variadores de Velocidade e Softstarters.
Disponível em: www.weg.com.br
WEBSITES CONSULTADOS
 WEG – http: //www.weg.com – Acesso em Agosto de 2012
 SIEMENS – Catálogo de Motores – http: //www.siemens.com.br
Apêndece
80

102. Este apêndice apresenta os arquivos necessários para simulação do sistema utilizando o SIMULINK do
software MATLAB.
clc
clear
%PROGRAMA PARA LA DETERMINACION DE LAS CARACTERISTICAS ENERGETICAS
%DEL MOTOR DE INDUCCION A PARTIR DE LOS DATOS DE CHAPA O DE CATALOGO.
%DATOS DE CHAPA
Pn=18.5;% potencia nominal en kW
pn=Pn*1000; %potencia nominal en W
fn=50;%frecuencia nominal
unf=400/1.73;% tensión nominal de fase (depende de la conexión)
inf=34.5;% corriente nominal de fase (depende de la conexión)
ns=1500;% velocidad sincrónica en r/min
nn=1450;% velocidad nominal en r/min
efn=0.901;% eficiencia nominal en pu
fpn=0.86;% factor de potencia nominal en pu
mm=2.9;% par máximo en por unidad de nominal
%CALCULO DE LAS PERDIDAS NOMINALES Y LOS PARAMETROS DEL CIRCUITO
%EQUIVALENTE
Mn=pn/(nn*0.105);% par nominal en N-m
sn=(ns-nn)/ns;% deslizamiento nominal en pu
penn=pn/efn; %potencia nominal de entrada en W
sperdn=penn-pn; %pérdidas nominales
pacn=0.2*sperdn;% pérdidas de acero nominales
kfb=0.5052*(pn^(-0.3296));% constante de las pérdidas mecánicas
pmecn=kfb*pn;%pérdidas mecánicas nominales
%Determinación de las pérdidas adicionales nominales en dependencia de la
%potendcia.
if Pn<100
padn=0.018*pn;
else
padn=0.015*pn;
end
zb=unf/inf;%impedancia base
rr=sn*zb;%resistencia del rotor en pu
senfin=sqrt(1-fpn^2);% seno del ángulo del factor de potencia
%Cálculo del deslizamiento para el par máximo
a1=2*mm*sn;a2=2*sn;b=sqrt(mm^2-(1+a2)+a1);c=(mm+b)/((1+a2)-a1);
sm=sn*c;%deslizamiento para el par máximo
ion=inf*(senfin-(sn/sm)*fpn);%Corriente de vacío nominal
xcc=rr/sm;%reactancia de dispersión total en ohms
a0=0.4;b0=0.6;%constantes para la división de la reactancia total
x1=a0*xcc;%reactancia de dispersión del estator
x2=b0*xcc;%reactancia de dispersión del rotor
i2n=inf*sqrt(1+(sn/sm)^2)*fpn;%corriente nominal del rotor
pcobrn=3*i2n^2*rr% pérdidas de cobre nominales en el rotor
pcobsn=sperdn-(pcobrn+padn+pmecn+pacn)%pérdidas de cobre nominales en el estator
rs=pcobsn/(3*inf^2);%resistencia del estator
e2n=unf-inf*rs*fpn-inf*x1*senfin;%fem nominal
rm=(3*e2n^2)/pacn;%resistencia de las pérdidas de acero
xm=e2n/ion; %Reactancia magnetizante
rad=padn/(3*i2n^2);%resistencia de las pérdidas adicionales
sperdn,pacn,pmecn,padn,pcobrn,pcobsn %pérdidas
rs,rr,rm,rad,xm,x1,x2%parámetros
%DETERMINACION DE LAS CARACTERISTICAS DE COMPORTAMIENTO DEL MOTOR
urf=400/1.73;%Tensión real de fase aplicada al motor
k=1;it(k)=1;s(k)=0.00001;
while s(k)<1.3*sn
zr=(rr/s(k)+rad)+x2*i;%impedancia de la rama del rotor
81

103. zm=(rm*xm*i)/(rm+xm*i);%impedancia de la rama magnetizante
z2=zr*zm/(zr+zm);%impedancias en paralelo
zs=rs+x1*i;%impedancia del estator
zt=zs+z2;%impedancia total
isc=urf/zt;%corriente del estator compleja
is(k)=abs(isc)/inf;%valor absoluto de la corriente del estator en pu
fi=angle(isc);%angulo del factor de potencia
fp(k)=cos(angle(isc));%factor de potencia
q(k)=-3*urf*is(k)*inf*sin(angle(isc))/penn;%potencia reactiva en por unidad
nr(k)=1-s(k);%velocidad del rotor en pu
up=isc*z2;%fem compleja
e2=abs(up);%fem absoluta
i22=up/zr;%corriente del rotor compleja
ir=abs(i22);%valor absoluto de la corriente del rotor
rr2=rr*(1-s(k))/s(k);%resistencia que simula la carga mecánica
Pmec=3*ir^2*rr2;%potencia convertida a la forma mecánica
pmec=pmecn*(nr(k)*ns)/nn;%pérdidas mecánicas
psal(k)=(Pmec-pmec)/pn;%potencia de salida en pu
pin(k)=3*urf*abs(isc)*fp(k)/pn;%potencia activa de entrada en pu
ef(k)=psal(k)/pin(k);
k=k+1;
s(k)=s(k-1)+0.0005;
it(k)=it(k-1)+1;
if it(k)>250
break
end
end
figure(1):plot(psal,ef,'r');grid
figure(2):plot(psal,fp,'r');grid
figure(3):plot(psal,q,'b');grid
figure(4):plot(psal,is,'r');grid
figure(5):plot(psal,nr,'b');grid
Pen=16
penpu=Pen/Pn
Ileida=inf*spline(pin,is,penpu)
ipu=Ileida/inf
Psal=pn*spline(is,psal,ipu)
Qen=penn*spline(is,q,ipu)
ef1=spline(is,ef,ipu)
82