Este documento apresenta os conceitos fundamentais da computação gráfica, incluindo sistemas gráficos, hardware gráfico, sistemas de coordenadas, dispositivos de visualização e entrada, algoritmos para desenho de primitivas gráficas e preenchimento de polígonos, e transformações 2D e 3D.

1. Apostila de Computa¸˜o Gr´fica
ca a
Agma Juci Machado Traina
Maria Cristina Ferreira de Oliveira
16 de maio de 2006

2. Resumo
Este ´ o material utilizado no Instituto de Ciˆncias matem´ticas e de Computa¸˜o da USP-S˜o Carlos
e e a ca a
para as disciplinas de computa¸˜o gr´fica ministradas pelas Profa. Dra. Agma Juci Machado Traina e
ca a
Profa. Dra. Maria Cristina Ferreira de Oliveira.

3. Sum´rio
a
Sum´rio
a 2
Lista de Figuras 5
1 Introdu¸˜o ` Computa¸˜o Gr´fica
ca a ca a 8
1.1 Sistemas Gr´ficos . . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.2 Aplica¸˜es da CG . . . . . . . . . .
co . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.3 Hardware Gr´fico . . . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.4 Resolu¸˜o Gr´fica . . . . . . . . . .
ca a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.5 Sistemas de Coordenadas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.6 Exerc´ıcios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2 Dispositivos de Visualiza¸˜o ca 15
2.1 Dispositivos Gr´ficos Vetoriais . . . . . . . . . . . . . . . . . . . . . .
a . . . . . . . . . . . 15
2.1.1 Tra¸adores Digitais . . . . . . . . . . . . . . . . . . . . . . . . .
c . . . . . . . . . . . 15
2.1.2 Dispositivos de V´ ıdeo Vetoriais (Vector Refresh Display Tubes) . . . . . . . . . . . 15
2.1.3 Terminais CRT com mem´ria (Direct View Storage Tubes) . .
o . . . . . . . . . . . 17
2.2 Primitivas de Software para Dispositivos Vetoriais . . . . . . . . . . . . . . . . . . . . . . 17
2.3 Dispositivos Gr´ficos Matriciais . . . . . . . . . . . . . . . . . . . . . .
a . . . . . . . . . . . 17
2.3.1 Impressoras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.3.2 Dispositivos de V´ ıdeo de Varredura (Raster Scanning VDUs) . . . . . . . . . . . . 18
2.3.3 Primitivas de Software . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.4 Exerc´ıcios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.5 Dispositivos de Entrada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.5.1 Teclado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5.2 Ligth Pen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5.3 Joystick . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5.4 Mouse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5.5 Mesa Digitalizadora (Tablet) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5.6 Data Glove . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.5.7 Outros dispositivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3 Tra¸ado de Curvas em Dispositivos Gr´ficos Matriciais
c a 23
3.1 Simetria e Reflex˜o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a 24
3.2 Convers˜o Matricial de Segmentos de Reta . . . . . . . . . . . . . . . . . . . . . . . . . .
a 24
3.2.1 Caracter´ ısticas Desej´veis para os Algoritmos de convers˜o Matricial de Segmentos
a a
de Retas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2.2 Crit´rio Adotado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 25
3.2.3 Algoritmos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.2.4 Algoritmo do “Ponto-M´dio” . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 26
3.3 Convers˜o Matricial de Circunferˆncias . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a e 29
3.3.1 Simetria de ordem 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.3.2 Algoritmo do “Ponto-M´dio” para Circunferˆncias . . . . . . . . . . . . . . . . . .
e e 31
3.4 Convers˜o Matricial de Elipses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a 34
3.5 Corre¸˜o no Tra¸ado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca c 37
3.6 Antialising . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
´
3.6.1 Amostragem de Areas n˜o Ponderada . . . . . . . . . . . . . . . . . . . . . . . . .
a 38
2

4. 4 Preenchimento de Pol´ ıgonos 42
4.1 Retˆngulos . . . . . . . . . . . . . . . . . . . . . . . . . . .
a . . . . . . . . . . . . . . . . . 42
4.2 Pol´ıgonos de Forma Arbitr´ria . . . . . . . . . . . . . . . .
a . . . . . . . . . . . . . . . . . 43
4.2.1 Arestas Horizontais . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
4.2.2 Slivers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.2.3 Algoritmo para Convers˜o Matricial de Segmento de
a Reta que Utiliza “Coerˆncia
e
de Arestas” de um Pol´ ıgono . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
5 Transforma¸˜es 2D e 3D
co 50
5.1 Transforma¸˜es em 2D . . . . . . . . . . . . . . . . . . . . . . . .
co . . . . . . . . . . . . . . 50
5.2 Coordenadas Homogˆneas e Matrizes de Transforma¸˜o . . . . .
e ca . . . . . . . . . . . . . . 52
5.3 Transforma¸˜es 2D Adicionais: Espelhamento e Shearing . . . .
co . . . . . . . . . . . . . . 55
5.3.1 Espelhamento (Mirror) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
5.3.2 Shearing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
5.4 Transforma¸˜es entre sistemas de coordenadas . . . . . . . . . .
co . . . . . . . . . . . . . . 57
5.5 Composi¸˜o de Transforma¸˜es . . . . . . . . . . . . . . . . . . .
ca co . . . . . . . . . . . . . . 58
5.6 Transforma¸˜o Janela - Porta de Vis˜o (“Window-to-Viewport”)
ca a . . . . . . . . . . . . . . 59
5.7 Eficiˆncia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . 61
5.8 Transforma¸˜es em 3D . . . . . . . . . . . . . . . . . . . . . . . .
co . . . . . . . . . . . . . . 63
5.8.1 Composi¸˜o de Transforma¸˜es em 3D . . . . . . . . . . .
ca co . . . . . . . . . . . . . . 64
6 Observa¸˜o de Cenas 3D
ca 69
6.1 Pipeline de observa¸˜o (“viewing pipeline”) . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 69
6.2 Coordenadas de Observa¸˜o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 70
6.2.1 Especifica¸˜o do sistema de coordenadas de observa¸˜o . . . . . . . . . . . . . . .
ca ca 70
6.2.2 Transforma¸˜o do sistema de coordenadas do mundo para o sistema de coordenadas
ca
de observa¸˜o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 71
6.3 Proje¸˜es . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
co 73
6.3.1 Proje¸˜o Perspectiva . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 73
6.3.2 Desenvolvimento Matem´tico para Proje¸˜es Paralelas . . . . . . . . . . . . . . . .
a co 77
7 Recorte de Primitivas 2D 78
7.1 Recorte de segmentos de reta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
7.1.1 Recorte de Pontos Extremos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
7.1.2 Algoritmo de Cohen-Sutherland para Recorte de Segmentos de Reta . . . . . . . . 79
7.2 Recorte de Circunferˆncias . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . 81
8 Curvas e Superf´ ıcies em Computa¸˜o Gr´fica
ca a 86
8.1 Representa¸˜o de Curvas . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca . . . . . . . . . . 86
8.2 Curve Fitting x Curve Fairing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
8.2.1 Ajuste de curvas (curve fitting) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
8.2.2 Aproxima¸˜o de curvas (curve fairing) . . . . . . . . . . . . . . .
ca . . . . . . . . . . 87
8.3 Representa¸˜es Param´tricas e N˜o Param´tricas (expl´
co e a e ıcita e impl´ıcita) . . . . . . . . . . 87
8.3.1 Limita¸˜es das representa¸˜es n˜o param´tricas . . . . . . . . . .
co co a e . . . . . . . . . . 88
8.4 Curvas de B´zier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 90
9 Apostila Modelagem 93
10 Rendering 94
11 Cores e Sistemas de Cores 95
11.1 Percep¸˜o de Cor . . . . . . . . . . . . . .
ca . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
11.2 Sistemas de Cores Prim´rias . . . . . . . .
a . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
11.3 Modelo XYZ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
11.4 Modelo RGB (Red, Green, Blue) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
11.5 Modelo HSV (Hue, Saturation, Value) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
11.6 Modelo HLS (Hue, Lightness, Saturation) . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
3

5. 12 Processamento Digital de Imagens 102
12.1 Introdu¸˜o . . . . . . . . . . . . . . . . . .
ca . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
12.2 Considera¸˜es Sobre Imagens . . . . . . .
co . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
12.3 Tabelas “Look-up” . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
12.4 Tipos de Manipula¸˜o de Imagens . . . .
ca . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
12.5 Transforma¸˜es Radiom´tricas . . . . . .
co e . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
12.5.1 Opera¸˜es Pontuais sobre Imagens
co . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
12.5.2 Opera¸˜es Locais Sobre a Imagem
co . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
Bibliografia 113
A Hist´rico
o 114
4

6. Lista de Figuras
1.1 Relacionamento entre as 3 sub´reas da Computa¸˜o Gr´fica. . . . . . . . . . . . . . . . .
a ca a 8
1.2 Esquema b´sico de um hardware de computa¸˜o gr´fica. . . . . . . . . . . . . . . . . . . .
a ca a 12
1.3 Sistemas de coordenadas e suas transforma¸˜es. . . . . . . . . . . . . . . . . . . . . . . . .
co 13
2.1 Estrutura interna de um CRT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.2 Convers˜o Digital-Anal´gica para Visualiza¸˜o num CRT. . . . . . . . . . . . . . . . . . .
a o ca 16
2.3 Uma seq¨ˆncia de bits na mem´ria de imagem ´ convertida para uma seq¨ˆncia de pixels
ue o e ue
na tela. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.4 Representa¸˜o esquem´tica de uma imagem matricial e sua representa¸˜o num frame buffer.
ca a ca 18
2.5 Varredura por rastreio fixo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.6 Representa¸˜o esquem´tica de um CRT por varredura colorido. . . . . . . . . . . . . . . .
ca a 19
2.7 Organiza¸˜o de uma v´
ca ıdeo look-up table. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.1 Representa¸˜o de segmentos de reta horizontais, verticais e diagonais. . . . . . . . . . . .
ca 23
3.2 Reflex˜o de uma imagem com rela¸˜o a um eixo diagonal. . . . . . . . . . . . . . . . . . .
a ca 24
3.3 Rota¸˜o de 90o obtida atrav´s de 2 reflex˜es, uma horizontal (a) e outra na diagonal (b).
ca e o 24
3.4 Convers˜es matriciais de um segmento de reta resultante de diferentes crit´rios. . . . . . .
o e 25
3.5 Imagens de segmentos de reta convertidos pelo crit´rio expl´
e ıcito acima. . . . . . . . . . . . 26
3.6 Grade de pixels para o Algoritimo o Ponto-M´dio (M) e as escolhas E e NE. . . . . . . . .
e 27
3.7 Grade de pixels para o Algoritimo o Ponto-M´dio (M) e as escolhas E e NE. . . . . . . . .
e 29
3.8 Um arco de 1 de circunferˆncia, obtido variando-se x em incrementos unit´rios, e calcu-
4 e a
lando e arrendondando y. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.9 Oito pontos sim´tricos em uma circunferˆncia. . . . . . . . . . . . . . . . . . . . . . . . .
e e 31
3.10 Malha de pixels para o Algoritmo do Ponto-M´dio para circunferˆncias, ilustrando a escolha
e e
entre os pixels E e SE. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.11 Segundo octante da circunferˆncia gerado com o algor´
e ıtimo do Ponto-M´dio e primeiro
e
octante gerado por simetria. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.12 Elipse padr˜o centrada na origem. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a 36
3.13 As duas regi˜e adotadas, definidas pela tangente a 45o . . . . . . . . . . . . . . . . . . . . .
o 36
3.14 Segmento de reta renderizado com o algor´ ıtmo do ponto m´dio em diferentes escalas. (a)
e
´ uma aplia¸˜o da regi˜o central de (b). . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e ca a 38
3.15 Segmento de reta definido com uma espessura diferente de zero. . . . . . . . . . . . . . . . 39
3.16 A intensidade do pixel ´ proporcional ` area coberta. . . . . . . . . . . . . . . . . . . . . .
e a 39
3.17 Filtro definido por um cubo para um pixel definido por um quadrado. . . . . . . . . . . . 40
3.18 Filtro cˆnico com diˆmetro igual ao dobro da largura de um pixel. . . . . . . . . . . . . .
o a 40
4.1 Esta figura ilustra o processo de linha de varredura para um pol´ ıgono arbitr´rio. As
a
intersec¸˜es da linha de varredura 8 com os lados FA e CD possuem coordenadas inteiras,
co
enquanto as intersec¸˜es com os lados EF e DE possuem coordenadas reais. . . . . . . . .
co 43
4.2 Linhas de varredura em um pol´ ıgno. Os extremos em preto, e os pixels no interior em
cinza. (a) Extremo calculado pelo algoritmo do ”Meio-Ponto”. (b) Extremo interior ao
pol´
ıgno. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
4.3 Tratamento dos lados horizontais de um pol´ ıgono. . . . . . . . . . . . . . . . . . . . . . . 45
4.4 Exemplo de uma convers˜o matricial de um Sliver . . . . . . . . . . . . . . . . . . . . . .
a 46
4.5 ET para o pol´ıgono de Figura 4.1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
4.6 AET para o pol´ ıgono da Figura 4.1 a) linha de varredura 9 b) linha de varredura 10. Note
que a coordenada x da aresta DE em (b) foi arredondada para cima.. . . . . . . . . . . . . 48
5.1 Transla¸˜o de uma casa. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 51
5.2 Mudan¸a de escala de uma casa. Como a escala ´ n˜o uniforme, sua propor¸˜o ´ alterada.
c e a ca e 51
5

7. 5.3 Esta figura mostra a rota¸˜o da casa por 45◦ . Da mesma forma que para a escala, a rota¸˜o
ca ca
tamb´m ´ feita em rela¸˜o a origem. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e e ca 52
5.4 Derivando a equa¸˜o de rota¸˜o. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca ca 52
5.5 O espa¸o de Coordenadas Homogˆneas XY W , com o plano W = 1 e o ponto P (X, Y, W )
c e
projetado sobre o plano W = 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
5.6 Um cubo unit´rio ´ rodados 45 graus, posteriormente escalado n˜o uniformemente. Obtem-
a e a
se dessa forma uma transforma¸˜o afim. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 54
5.7 Reflex˜o de um objeto em torno do eixo x. . . . . . . . . . . . . . . . . . . . . . . . . . .
a 55
5.8 Reflex˜o de um objeto em torno de um eixo perpendicular ao plano xy, passando pela origem.
a 56
5.9 Rota¸˜o em rela¸˜o ao Ponto P 1, por um ˆngulo θ. . . . . . . . . . . . . . . . . . . . . . .
ca ca a 58
5.10 Escala e rota¸˜o de uma casa em rela¸˜o ao ponto P1 . . . . . . . . . . . . . . . . . . . . .
ca ca 59
5.11 Janela em Coordenadas do mundo e porta de vis˜o em coordenadas de tela. . . . . . . . .
a 60
5.12 Duas portas de vis˜o associadas a mesma janela. . . . . . . . . . . . . . . . . . . . . . . .
a 60
5.13 Os passos da transforma¸˜o janela - porta de vis˜o. . . . . . . . . . . . . . . . . . . . . . .
ca a 61
5.14 Primitivas gr´ficas de sa´ em coordenadas do mundo s˜o recortadas pela janela. O seu
a ıda a
interior ´ apresentado na tela (viewport). . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 61
5.15 Sistema de Coordenadas dado pela Regra da M˜o Direita. . . . . . . . . . . . . . . . . . .
a 63
5.16 Transformando P1 , P2 e P3 da posi¸˜o inicial em (a) para a posi¸˜o final em (b). . . . . .
ca ca 65
5.17 Rota¸˜o dos pontos P1 , P2 e P3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 66
5.18 Rota¸˜o em rela¸˜o ao eixo x. P1 e P2 de comprimento D2 ´ rotacionado em dire¸˜o ao
ca ca e ca
eixo z, pelo ˆngulo positivo f. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a 66
5.19 Rota¸˜o em rela¸˜o ao eixo z. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca ca 67
5.20 Os vetores unit´rios Rx , Ry e Rz , os quais s˜o transformados nos eixos principais. . . . .
a a 68
6.1 Atributos da cˆmera [Schr¨eder, 1998]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a o 69
6.2 Movimentos de cˆmera [Schr¨eder, 1998]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
a o 70
6.3 Movimentos de cˆmera [Schr¨eder, 1998]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
a o 71
6.4 Um VCS baseado na regra da m˜o direita com xv , yv e zv .relativos ao sistema de coorde-
a
nadas do mundo [Hearn and Baker, 1994]. . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
6.5 Orienta¸˜es do plano de observa¸˜o conforme o vetor normal. O vetor (1, 0, 0) d´ a ori-
co ca a
enta¸˜o em (a) e (1, 0, 1), a orienta¸˜o em (b) [Hearn and Baker, 1994]. . . . . . . . . . .
ca ca 72
6.6 Taxomia de proje¸˜es [Plastock and Kalley, 1999]. . . . . . . . . . . . . . . . . . . . . . .
co 73
6.7 Linha AB e sua proje¸˜o A’B’: (a) perspectiva; (b) ortogonal. . . . . . . . . . . . . . . . .
ca 73
6.8 Proje¸˜es de um cubo (com 1 ponto de fuga) sobre um plano cortando o eixo Z, apresen-
co
tando o ponto de fuga. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
6.9 Proje¸˜es perspectivas com 2 pontos de fuga ( o plano de proje¸˜o intercepta 2 eixos (x e
co ca
z)). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
6.10 Proje¸˜es perspectivas com 3 pontos de fuga ( o plano de proje¸˜o intercepta os 3 eixos).
co ca 75
6.11 A esfera B ´ bem maior que a esfera A, por´m ambas aparecem com o mesmo tamanho
e e
quando projetadas no plano de vis˜o. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a 75
6.12 Confus˜o visual da perpectiva (objeto atr´s do centro de proje¸˜o). . . . . . . . . . . . . .
a a ca 76
6.13 Proje¸˜o em perspectiva de um ponto P=(x, y, z) na posi¸˜o (xp, yp, zp) sobre o plano
ca ca
de proje¸˜o [Hearn and Baker, 1994]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ca 76
6.14 Proje¸˜o ortogonal de um ponto no plano de proje¸˜o [Hearn and Baker, 1994]. . . . . . .
ca ca 77
7.1 Exemplos de recorte de segmentos de reta. . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
7.2 C´digos das regi˜es. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
o o 80
7.3 Funcionamento do algoritmo de Cohen-Sutherland para recorte de segmentos. . . . . . . . 80
7.4 Algoritmo de Sutherland-Hodgman para Recorte de Pol´ ıgonos. . . . . . . . . . . . . . . . 83
7.5 Exemptos de recorte de pol´ıgonos. (a) M´ltiplos componentes. (b) Caso convexo (c) Caso
u
cˆncavo com muitas arestas exteriores. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
o 83
7.6 Quatro situa¸˜es poss´
co ıveis no recorte de pol´ ıgonos. . . . . . . . . . . . . . . . . . . . . . . 84
8.1 Representa¸˜o de superf´
ca ıcies atrav´s de malhas. . . . . . . .
e . . . . . . . . . . . . . . . . . 86
8.2 Aproxima¸˜o de curvas por segmentos de reta conectados. .
ca . . . . . . . . . . . . . . . . . 87
8.3 Aproxima¸˜o de curvas por segmentos de reta conectados. .
ca . . . . . . . . . . . . . . . . . 88
8.4 Pontos de uma circunferˆncia. . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 90
8.5 Representa¸˜o de uma curva de B´zier definida pelos pontos
ca e B0 , B1 , B2 e B3 . . . . . . . . 90
8.6 Fun¸˜es de blending para v´rios valores de n. . . . . . . . .
co a . . . . . . . . . . . . . . . . . 91
11.1 Espectro eletromagn´tico [Gro94]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 95
6

8. 11.2 Ilustra¸˜o da mistura de cores aditivas [For94]. . . . . . . . . . . . . .
ca . . . . . . . . . . . 97
11.3 Ilustra¸˜o da mistura de cores subtrativas [For94]. . . . . . . . . . . .
ca . . . . . . . . . . . 97
11.4 Ilustra¸˜o da obten¸˜o de tints, shades e tones. . . . . . . . . . . . . .
ca ca . . . . . . . . . . . 97
11.5 Diagrama de cromaticidade do CIE [Hea94]. . . . . . . . . . . . . . . . . . . . . . . . . . . 98
11.6 Representa¸˜o de escalas de cor no diagrama de cromaticidade do CIE
ca [Hea94]. . . . . . . 99
11.7 Cubo do RGB [Fol96]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
11.8 Cone hexagonal do HSV [Fol96]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
11.9 Cone duplo do HLS [Fol96]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
12.1 Efeitos sobre uma imagem, de se reduzir o tamanho da grade de amostragem. . . . . . . . 103
12.2 Uma imagem de 512 x 512 pixels, quantizada em (a) 256 n´ ıveis, (b) 128 n´ ıveis, (c) 64
n´
ıveis, (d) 32 n´
ıveis, (e) 16 n´
ıveis, (f) 8 n´ıveis, (g) 4 n´
ıveis e (h) 2 n´ıveis de cinza. . . . . . 104
12.3 Representa¸˜o de um pixel P com 8-bits (8 planos) de profundidade. . . . . . . . . . . . .
ca 104
12.4 Organiza¸˜o de uma LUT, para um sistema de pixels de 8 bits. . . . . . . . . . . . . . . .
ca 105
12.5 Imagens e histogramas de intensidade. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
12.6 Efeito de uma transforma¸˜o dos n´
ca ıveis de cinza efetuado sobre o histograma. . . . . . . . 107
12.7 Manipula¸˜o de janelas de intensidade da imagem atrav´s do histograma. . . . . . . . . .
ca e 107
12.8 Sinais “ru´ıdo” (a) e “degrau” (b). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
12.9 Sinais “ru´ıdo” (a) e “degrau” (b). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
12.10Efeitos de filtros lineares ao “ru´ ıdo” e ` “borda”: (a) efeitos de atenua¸˜o; (b) borramento
a ca
da borda; (c) amplia¸˜o do ru´
ca ıdo; (d) realce da borda. . . . . . . . . . . . . . . . . . . . . 110
12.11Efeito do filtro da mediana sobre o “ru´ ıdo” e o “degrau”. . . . . . . . . . . . . . . . . . . 110
12.12Uma transforma¸˜o geom´trica de 90o graus. . . . . . . . . . . . . . . . . . . . . . . . . . .
ca e 111
7

9. Cap´
ıtulo 1
Introdu¸˜o ` Computa¸˜o Gr´fica
ca a ca a
A Computa¸˜o Gr´fica ´ a ´rea da ciˆncia da computa¸˜o que estuda a gera¸˜o, manipula¸˜o e inter-
ca a e a e ca ca ca
preta¸˜o de modelos e imagens de objetos utilizando computador. Tais modelos vˆm de uma variedade
ca e
de disciplinas, como f´
ısica, matem´tica, engenharia, arquitetura, etc.
a
Pode-se relacionar a Computa¸˜o Gr´fica com 3 sub-´reas [Persiano and Oliveira, 1989]:
ca a a
• S´
ıntese de Imagens: ´rea que se preocupa com a produ¸˜o de representa¸˜es visuais a partir
a ca co
co e ´
das especifica¸˜es geom´trica e visual de seus componentes. E freq¨entemente confundida com a
u
pr´pria Computa¸˜o Gr´fica. As imagens produzidas por esta sub-´rea s˜o geradas a partir de
o ca a a a
dados mantidos nos chamados Display-Files.
• Processamento de Imagens: envolve as t´cnicas de transforma¸˜o de Imagens, em que tanto
e ca
a imagem original quanto a imagem resultado apresentam-se sob uma representa¸˜o visual (ge-
ca
ralmente matricial). Estas transforma¸˜es visam melhorar as caracter´
co ısticas visuais da imagem
(aumentar contraste, foco, ou mesmo diminuir ru´ ıdos e/ou distor¸˜es). As imagens produzi-
co
das/utilizadas por esta sub-´rea s˜o armazenadas/recuperadas dos chamados Raster-Files.
a a
• An´lise de Imagens: ´rea que procura obter a especifica¸˜o dos componentes de uma imagem a
a a ca
partir de sua representa¸˜o visual. Ou seja a partir da informa¸˜o pict´rica da imagem (a pr´pria
ca ca o o
imagem!) produz uma informa¸˜o n˜o pict´rica da imagem (por exemplo, as primitivas geom´tricas
ca a o e
elementares que a comp˜em).
o
Figura 1.1: Relacionamento entre as 3 sub´reas da Computa¸˜o Gr´fica.
a ca a
Na ultima d´cada somou-se a esse contexto a ´rea de Visualiza¸˜o de Dados, tamb´m chamada
´ e a ca e
Visualiza¸˜o Computacional [Minghim and Oliveira, 1997, Schr¨eder et al., 1996], que usa t´cnicas de
ca o e
Computa¸˜o Gr´fica para representar informa¸˜o, de forma a facilitar o entendimento de conjuntos de
ca a ca
dados num´ricos de alta complexidade. Exemplos de ´reas de aplica¸˜o s˜o: visualiza¸˜o de imagens
e a ca a ca
m´dicas, meteorologia, dados financeiros, visualiza¸˜o de programas, dinˆmica dos fluidos, e muitas
e ca a
8

10. outras. Nelas, o que existe em comum ´ que a representa¸˜o gr´fica (superf´
e ca a ıcies, part´ıculas, ´
ıcones) s˜oa
geradas automaticamente a partir do conjunto de dados. Ao usu´rio cabe definir parˆmetros e atributos
a a
da imagem para melhor “navegar” seu conjunto de dados. Dessa maneira, a visualiza¸˜o de dados partilha
ca
de caracter´ısticas da s´ ıntese, do processamento e da an´lise de dados.
a
Atualmente a Computa¸˜o Gr´fica ´ altamente interativa: o usu´rio controla o conte´do, a estrutura
ca a e a u
e a aparˆncia dos objetos e suas imagens visualizadas na tela, usando dispositivos como o teclado e o
e
mouse. Entretanto, at´ o in´
e ıcio dos anos 80, a computa¸˜o gr´fica era uma disciplina restrita e alta-
ca a
mente especializada. Devido principalmente ao alto custo do hardware, poucos programas aplicativos
exploravam gr´ficos. O advento dos computadores pessoais de baixo custo, como o IBM-PC e o Apple
a
Macintosh, com terminais gr´ficos de varredura (raster graphics displays), popularizou o uso de gr´ficos
a a
na intera¸˜o usu´rio-computador.
ca a
Os displays gr´ficos de baixo custo possibilitaram o desenvolvimento de in´meros aplicativos baratos
a u
e f´ceis de usar, que dispunham de interfaces gr´ficas - planilhas, processadores de texto, programas de
a a
desenho... As interfaces evoluiram e introduziu-se o conceito de desktop - uma met´fora para uma mesa
a
de trabalho. Nessas interfaces gr´ficas, atrav´s de um gerenciador de janelas (window manager ) o usu´rio
a e a
pode criar e posicionar janelas que atuam como terminais virtuais, cada qual executando aplicativos in-
dependentemente. Isso permite que o usu´rio execute v´rios aplicativos simultaneamente, e selecione um
a a
deles a um simples toque no mouse. ´ Icones (icons) s˜o usados para representar arquivos de dados, progra-
a
mas e abstra¸˜es de objetos de um escrit´rio - como arquivos, caixas de correio (mailboxes), impressoras,
co o
latas de lixo - nas quais s˜o executadas opera¸˜es an´logas `s da vida real. Para ativar os programas, o
a co a a
usu´rio pode selecionar ´
a ıcones, ou usar buttons e menus dinˆmicos. Objetos s˜o manipulados diretamente
a a
atrav´s de opera¸˜es de pointing e clicking feitas com o mouse. Atualmente, mesmo aplicativos que ma-
e co
nipulam texto (como processadores de texto) ou dados num´ricos (como planilhas) usam interfaces desse
e
tipo, reduzindo sensivelmente a intera¸˜o textual por meio de teclados alfanum´ricos.
ca e
A computa¸˜o gr´fica n˜o ´ mais uma raridade: ´ parte essencial de qualquer interface com o usu´rio,
ca a a e e a
´ indispens´vel para a visualiza¸˜o de dados em 2D e 3D e tem aplica¸˜es em ´reas como educa¸˜o,
e a ca co a ca
ciˆncias, engenharia, medicina, publicidade, lazer, militar, ...
e
A computa¸˜o gr´fica trata da s´
ca a ıntese de imagens de objetos reais ou imagin´rios a partir de modelos
a
computacionais. Processamento de imagens ´ uma ´rea relacionada que trata do processo inverso: a
e a
an´lise de cenas, ou a reconstru¸˜o de modelos de objetos 2D ou 3D a partir de suas imagens.
a ca
Note que a s´ ıntese de imagens parte da descri¸˜o de objetos tais como segmentos de reta, pol´
ca ıgonos,
poliedros, esferas, etc.; e produz uma imagem que atende a certas especifica¸˜es e que pode, em ultima
co ´
instˆncia, ser visualizada em algum dispositivo (terminal de v´
a ıdeo, plotter, impressora, filme fotogr´fico...).
a
As imagens em quest˜o constituem uma representa¸˜o visual de objetos bi- ou tridimensionais descritos
a ca
atrav´s de especifica¸˜es abstratas.
e co
O processamento de imagens parte de imagens j´ prontas para serem visualizadas, as quais s˜o trans-
a a
feridas para o computador por mecanismos diversos - digitaliza¸˜o de fotos, tomadas de uma cˆmera de
ca a
v´ıdeo, ou imagens de sat´lite - para serem manipuladas visando diferentes objetivos.
e
1.1 Sistemas Gr´ficos
a
A Computa¸˜o Gr´fica (especialmente as componentes relativas a gr´ficos 3D e a gr´ficos 3D interativos)
ca a a a
desenvolveu-se de modo bem diverso: de simples programas gr´ficos para computadores pessoais ` pro-
a a
gramas de modelagem e de visualiza¸˜o em workstations e supercomputadores. Como o interesse em CG
ca
cresceu, ´ importante escrever aplica¸˜es que possam rodar em diferentes plataformas. Um padr˜o para
e co a
desenvolvimento de programas gr´ficos facilita esta tarefa eliminando a necessidade de escrever c´digo
a o
para um driver gr´fico distinto para cada plataforma na qual a aplica¸˜o deve rodar. Para se padronizar
a ca
a constru¸˜o de aplicativos que se utilizam de recursos gr´ficos e torn´-los o mais independentes poss´
ca a a ıvel
de m´quinas, e portanto facilmente port´veis, foram desenvolvidos os chamados Sistemas Gr´ficos.
a a a
V´rios padr˜es tiveram sucesso integrando dom´
a o ınios espec´
ıficos. Por exemplo, a linguagem Postscript
que se tornou um padr˜o por facilitar a publica¸˜o de documentos est´ticos contendo gr´ficos 2D e textos.
a ca a a
Outro exemplo ´ o sistema XWindow, que se tornou padr˜o para o desenvolvimento de interfaces gr´ficas
e a a
2D em workstations UNIX. Um programador usa o X para obter uma janela em um display gr´fico no a
qual um texto ou um gr´fico 2D pode ser desenhado. A ado¸˜o do X pela maioria dos fabricantes de
a ca
workstation significa que um unico programa desenvolvido em X pode ser rodado em uma variedade de
´
workstation simplesmente recompilando o c´digo. Outra facilidade do X ´ o uso de redes de computadores:
o e
um programa pode rodar em uma workstation e ler a entrada e ser exibido em outra workstation, mesmo
de outro fabricante.
Para gr´ficos 3D foram propostos v´rios padr˜es. A primeira tentativa foi o Sistema Core - Core
a a o
Graphics System - (1977 e 1979) pelos americanos. Mas a primeira especifica¸˜o gr´fica realmente pa-
ca a
9

11. dronizada foi o GKS - Graphical Kernel System, pela ANSI e ISO em 1985. O GKS ´ uma vers˜o maise a
elaborada que o Core. O GKS suporta um conjunto de primitivas gr´ficas interrelacionadas, tais como:
a
desenho de linhas, pol´ ıgonos, caracteres, etc., bem como seus atributos. Mas n˜o suporta agrupamentos
a
de primitivas hier´rquicas de estruturas 3D. Um sistema relativamente famoso ´ PHIGS (Programmer’s
a e
Hierarchical Interactive Graphics System). Baseado no GKS, PHIGS ´ um padr˜o ANSI. PHIGS (e seu
e a
descendente, PHIGS+) provˆem meios para manipular e desenhar objetos 3D encapsulando descri¸˜es de
e co
objetos e atributos em uma display list. A display list ´ utilizada quando o objeto ´ exibido ou manipu-
e e
lado, uma vantagem ´ a possibilidade de descrever um objeto complexo uma unica vez mesmo exibindo-o
e ´
v´rias vezes. Isto ´ especialmente importante se o objeto a ser exibido deve ser transmitido por uma
a e
rede de computadores. Uma desvantagem da display list ´ a necessidade de um esfor¸o consider´vel
e c a
para reespecificar um objeto que est´ sendo modelado interativamente pelo usu´rio. Uma desvantagem
a a
do PHIGS e PHIGS+ (e GKS) ´ que eles n˜o tˆm suporte a recursos avan¸ados como mapeamento de
e a e c
textura.
O XWindow ganhou uma extens˜o para o PHIGS, conhecida como PEX, de modo que o X pudesse
a
manipular e desenhar objetos 3D. Entre outras extens˜es, PEX soma-se de modo imediato ao PHIGS,
o
assim um objeto pode ser exibido durante a sua defini¸˜o sem a necessidade da display list. O PEX
ca
tamb´m n˜o suporta recursos avan¸ados e s´ est´ dispon´ aos usu´rios do XWindow.
e a c o a ıvel a
O sistema gr´fico mais popular atualmente ´ o OpenGL (GL - Graphics Library) que provˆ carac-
a e e
ter´ısticas avan¸adas e pode ser utilizado em modo imediato ou com display list. OpenGL ´ um padr˜o
c e a
relativamente novo (sua primeira vers˜o ´ de 1992) e ´ baseado na biblioteca GL das workstations IRIS da
a e e
Silicon Graphics. Atualmente um cons´rcio de ind´strias ´ respons´vel pela gerenciamento da evolu¸˜o do
o u e a ca
OpenGL. Existe uma implementa¸˜o livre (c´digo fonte dispon´
ca o ıvel) do OpenGL conhecida com MesaGL
ou Mesa3D.
Como os outros sistemas gr´ficos, OpenGL oferece uma interface entre o software e o hardware gr´fico.
a a
A interface consiste em um conjunto de procedimentos e fun¸˜es que permitem a um programador es-
co
pecificar os objetos e as opera¸˜es que os envolvem produzindo imagens de alta qualidade. Como o
co
PEX, o OpenGL integra/permite a manipula¸˜o de objetos (desenhos) 3D ao X, mas tamb´m pode ser
ca e
integrado em outros sistemas de janela (por exemplo, Windows/NT) ou pode ser usado sem um sistema
de janela. OpenGL provˆ controle direto sobre opera¸˜es gr´ficas fundamentais em 3D e 2D, incluindo
e co a
a especifica¸˜o de parˆmetros como matrizes de transforma¸˜o e coeficientes de ilumina¸˜o, m´todos
ca a ca ca e
de antialiasing e opera¸˜es sobre pixels, mas n˜o provˆ mecanismos para descrever ou modelar objetos
co a e
geom´tricos complexos.
e
1.2 Aplica¸˜es da CG
co
A lista de aplica¸˜es ´ enorme, e cresce rapidamente. Uma amostra significativa inclui:
co e
• Interfaces: a maioria dos aplicativos para computadores pessoais e esta¸˜es de trabalho atualmente
co
disp˜em de interfaces gr´ficas baseadas em janelas, menus dinˆmicos, ´
o a a ıcones, etc.
• Tra¸ado interativo de gr´ficos: aplicativos voltados para usu´rios em ciˆncia, tecnologia e
c a a e
neg´cios geram gr´ficos que ajudam na tomada de decis˜es, esclarecem fenˆmenos complexos e
o a o o
representam conjuntos de dados de forma clara e concisa.
• Automa¸˜o de escrit´rios e editora¸˜o eletrˆnica: o uso de gr´ficos na dissemina¸˜o de
ca o ca o a ca
informa¸˜es cresceu muito depois do surgimento de software para editora¸˜o eletrˆnica em com-
co ca o
putadores pessoais. Este tipo de software permite a cria¸˜o de documentos que combinam texto,
ca
tabelas e gr´ficos - os quais tanto podem ser “desenhados” pelo usu´rio ou obtidos a partir de
a a
imagens digitalizadas.
• Projeto e desenho auxiliado por computador: em CAD, sistemas gr´ficos interativos s˜o
a a
utilizados para projetar componentes, pe¸as e sistemas de dispositivos mecˆnicos, el´tricos, eletro-
c a e
mecˆnicos e eletrˆnicos. Isto inclui edif´
a o ıcios, carca¸as de autom´veis, avi˜es e navios, chips VLSI,
c o o
sistemas ´ticos, redes telefˆnicas e de computador. Eventualmente, o usu´rio deseja apenas produzir
o o a
desenhos precisos de componentes e pe¸as. Mais frequentemente, o objetivo ´ interagir com um
c e
modelo computacional do componente ou sistema sendo projetado, de forma a testar propriedades
estruturais, el´tricas ou t´rmicas, at´ atingir um projeto satisfat´rio.
e e e o
• Simula¸˜o e anima¸˜o para visualiza¸˜o cient´
ca ca ca ıfica, lazer, arte e publicidade: uma das
a
´reas que mais evoluiram na d´cada de 80 foi a visualiza¸˜o cient´
e ca ıfica. Cientistas e engenheiros
perceberam que n˜o poderiam interpretar as quantidades prodigiosas de dados produzidas por pro-
a
gramas em supercomputadores sem resumir os dados e identificar tendˆncias e fenˆmenos atrav´s
e o e
10

12. de representa¸˜es gr´ficas. Como resultado, surgiram anima¸˜es computadorizadas do comporta-
co a co
mento variante no tempo de objetos reais ou simulados. Tais anima¸˜es podem ser utilizadas para
co
estudar entidades matem´ticas abstratas e modelos matem´ticos de fenˆmenos como fluxo de flui-
a a o
dos, relatividade, rea¸˜es qu´
co ımicas e nucleares, deforma¸˜o de estruturas mecˆnicas sob diferente
ca a
tipos de press˜o, etc. Outras aplica¸˜es tecnol´gicas avan¸adas incluem a produ¸˜o de desenhos
a co o c ca
animados e efeitos especiais para filmes e comerciais de TV, que requerem mecanismos sofisticados
para modelar objetos e para representar luz e sombra.
• Controle de processos: sistemas de controle de tr´fego a´reo e espacial, sistemas de controle de
a e
refinarias e de usinas de energia mostram graficamente os dados coletados por sensores conectados
a componentes cr´ ıticos dos sistemas, de forma que os operadores possam responder adequadamente
a condi¸˜es cr´
co ıticas.
• Cartografia: a computa¸˜o gr´fica ´ usada para produzir representa¸˜es precisas e esquem´ticas
ca a e co a
de fenˆmenos naturais e geogr´ficos obtidos a partir da coleta de dados.
o a
• Arte: A arte por computador vem crescendo imensamente nos ultimos anos. E poss´
´ ´ ıvel utilizar
novos recursos de computa¸˜o gr´fica para produzir efeitos art´
ca a ısticos, como a extra¸˜o de texturas,
ca
padr˜es e estruturas a partir de fotos digitalizadas.
o
ca ´
• Gr´ficos de Apresenta¸˜o (Presentation Graphics): E a utiliza¸˜o de t´cnicas gr´ficas para
a ca e a
demonstra¸˜o de resultados, id´ias e gr´ficos, com o intuito de mostrar ou transmitir conhecimento
ca e a
espec´
ıfico como, por exemplo, em uma aula, ou reuni˜o, ou na contru¸˜o de material did´tico.
a ca a
Neste curso, estamos interessados principalmente em t´cnicas de s´
e ıntese de imagens bem como seu
relacionamento com o processamento de imagens. Tamb´m n˜o pretendemos explorar todo o escopo de
e a
aplica¸˜es da CG, mas estudar os conceitos gerais envolvidos na programa¸˜o das primitivas gr´ficas que
co ca a
est˜o por tr´s dessas aplica¸˜es.
a a co
1.3 Hardware Gr´fico
a
Um sistema de hardware para computa¸˜o gr´fica consiste essencialmente de dispositivos gr´ficos de
ca a a
entrada e sa´ (I/O) ligados a um computador (Figura 1.2). Ao conjunto de dispositivos de I/O gr´ficos
ıda a
alocados para utiliza¸˜o por uma unica pessoa por vez denomina-se genericamente de “esta¸˜o de trabalho
ca ´ ca
gr´fica”, ou graphics workstation. Um sistema gr´fico multi-usu´rio pode ter v´rias esta¸˜es gr´ficas, de
a a a a co a
forma que mais de um dos v´rios dispositivos de I/O dispon´
a ıveis podem estar conectados e utilizando
o computador hospedeiro. Como em CG ´ freq¨ente a manipula¸˜o de grandes quantidades de dados,
e u ca
o computador deve ser equipado de mem´ria secund´ria com alta capacidade de armazenagem. Al´m
o a e
disso, um canal de comunica¸˜o de alta velocidade ´ necess´rio para reduzir os tempos de espera. Isto
ca e a
normalmente ´ feito atrav´s de comunica¸˜o local sobre um barramento paralelo com velocidade de
e e ca
transmiss˜o de dados da ordem de um milh˜o de bits por segundo. Se o equipamento gr´fico est´ distante
a a a a
do processador (conex˜o remota), um canal de comunica¸˜o serial pode ser necess´rio. Transmiss˜o
a ca a a
serial ass´ıncrona pode ser feita a velocidades de at´ 19.2 kbps (milhares de bits por segundo). Mesmo tal
e
velocidade pode ser muito lenta para alguns objetivos como anima¸˜o gr´fica de alta resolu¸˜o, onde cada
ca a ca
frame de imagem pode ter um megabyte de dados. Um sistema de conex˜o ideal nesse caso ´ uma Local
a e
Area Network (LAN) como a Ethernet. Os dispositivos de sa´ gr´ficos podem ser de natureza digital
ıda a
ou anal´gica, resultando em duas classes de gr´ficos, denominados vector graphics (gr´ficos vetoriais),
o a a
que desenham figuras tra¸ando seq¨ˆncias de segmentos de reta (vetores); e raster graphics (gr´ficos de
c ue a
varredura, ou matriciais), que desenham figuras pelo preenchimento de uma matriz de pontos (pixels).
1.4 Resolu¸˜o Gr´fica
ca a
Virtualmente todos os dispositivos de I/O gr´ficos usam uma malha retangular de posi¸˜es endere¸´veis
a co ca
- a qual ´ denominada “retˆngulo de visualiza¸˜o”. A “resolu¸˜o gr´fica” de um dispositivo ´ o n´mero
e a ca ca a e u
de posi¸˜es (ou pontos, ou pixels) horizontais e verticais que ele pode distinguir. Existem 4 parˆmetros
co a
que definem a resolu¸˜o:
ca
1. ndh - o n´mero de posi¸˜es endere¸´veis horizontalmente.
u co ca
2. ndv - o n´mero de posi¸˜es endere¸´veis verticalmente.
u co ca
3. width - a largura do retˆngulo de visualiza¸˜o em mm.
a ca
11

13. Figura 1.2: Esquema b´sico de um hardware de computa¸˜o gr´fica.
a ca a
4. height - a altura do retˆngulo de visualiza¸˜o em mm.
a ca
A partir desses 4 parˆmetros, v´rios n´meros interessantes podem ser calculados:
a a u
ndh
1. resolu¸˜o horizontal: horiz res =
ca width
width
2. tamanho ponto horizontal: horiz dot size = ndh
ndv
3. resolu¸˜o vertical: vert res =
ca height
height
4. tamanho ponto vertical: vert dot size = ndv
5. total pontos endere¸´veis: total nr dots = ndh.ndv
ca
total nr dots
6. resolu¸˜o de ´rea: area res =
ca a (width.height)
vert dot size
7. raz˜o de aspecto gr´fica: aspect ratio =
a a horiz dot size
height
8. raz˜o de aspecto f´
a ısica: physical aspect ratio = width
Note que horiz res, vert res e area res definem resolu¸˜es f´
co ısicas, enquanto que ndh, ndv e total nr dots
definem resolu¸˜es gr´ficas. Dispositivos de visualiza¸˜o podem ter a mesma resolu¸˜o gr´fica, com re-
co a ca ca a
solu¸˜es f´
co ısicas muito diferentes. O ideal seria ter um aspect ratio igual ou pr´ximo de 1.
o
1.5 Sistemas de Coordenadas
Na CG ´ necess´rio definir sistemas de coordenadas para quantificar os dados que est˜o
e a a
sendo manipulados. J´ vimos que os dispositivos de visualiza¸˜o gr´fica matriciais consistem de uma
a ca a
matriz de pixels endere¸´veis, e um gr´fico ´ formado “acendendo” ou “apagando” um pixel. Os pixels
ca a e
s˜o endere¸ados por dois n´meros inteiros que d˜o suas coordenadas horizontal e vertical, dcx, e dcy,
a c u a
respectivamente, onde:
0 ≤ dcx ≤ ndhm1 ≡ ndh − 1 (1.1)
0 ≤ dcy ≤ ndvm1 ≡ ndv − 1 (1.2)
Na matriz de pixels, o valor dcx + 1 d´ o n´mero da coluna, e dcy + 1 d´ o n´mero da linha do pixel
a u a u
endere¸ado. O pixel endere¸ado como (0, 0) est´ geralmente no canto inferior esquerdo do retˆngulo de
c c a a
visualiza¸˜o. As coordenadas (dcx, dcy) s˜o chamadas de coordenadas do dispositivo, e podem assumir
ca a
apenas valores inteiros. Coordenadas do dispositivo podem variar bastante para diferentes equipamentos,
o que levou ` utiliza¸˜o de coordenadas normalizadas do dispositivo (NDC - normalized device coor-
a ca
dinates), para efeito de padroniza¸˜o (ndcx, ndcy). NDCs s˜o vari´veis reais, geralmente definidas no
ca a a
intervalo de 0 a 1:
0 ≤ ndcx ≤ 1 (1.3)
12

14. 0 ≤ ndcy ≤ 1 (1.4)
A coordenada NDC (0, 0) corresponde ` origem (0, 0) nas coordenadas do dispositivo, e a coordenada
a
NDC (1, 1) refere-se ao pixel no canto superior direito, que corresponde ao pixel (ndhm1, ndvm1) nas
coordenadas do dispositivo. A vantagem da utiliza¸˜o de NDCs ´ que padr˜es gr´ficos podem ser discuti-
ca e o a
dos usando um sistema de coordenadas independente de dispositivos gr´ficos espec´
a ıficos. Obviamente, os
dados gr´ficos precisam ser transformados do sistema de coordenadas independente para o sistema de co-
a
ordenadas do dispositivo no momento de visualiza¸˜o. O mapeamento de NDCs (reais) para coordenadas
ca
do dispositivo (inteiros) ´ “linear”, por exemplo:
e
dcx = round(ndcx.ndhm1) (1.5)
dcy = round(ndcy.ndvm1) (1.6)
Dois outros sistemas de coordenadas s˜o uteis. O primeiro ´ o sistema de cordenadas f´
a ´ e ısico, (pcx, pcy)
onde pcx ´ a distˆncia f´
e a ısica ao longo do eixo x a partir do extremo esquerdo do retˆngulo de visualiza¸˜o,
a ca
e pcy ´ a distˆncia f´
e a ısica ao longo do eixo y a partir do extremo inferior. As unidades de medida utilizadas
s˜o polegadas ou mil´
a ımetros. A transforma¸˜o de coordenadas f´
ca ısicas para coordenadas do dispositivo ´e
dada por:
pcx
dcx = trunc(ndhm1 ) (1.7)
width
pcy
dcy = trunc(ndvm1 ) (1.8)
height
O segundo ´ o sistema de coordenadas do mundo, ou sistema de coordenadas do usu´rio, que consiste
e a
de coordenadas cartesianas (x, y), num intervalo qualquer definido pelo usu´rio:
a
xmin ≤ x ≤ xmax (1.9)
ymin ≤ y ≤ ymax (1.10)
Os parˆmetros que definem o intervalo de valores de x e y, xmin, ymin, xmax e ymax, definem uma
a
a
´rea retangular no espa¸o bidimensional, denominada de janela. A transforma¸˜o de coordenadas do
c ca
usu´rio (x, y) para NDCs (ndcx, ndcy), denominada transforma¸˜o de visualiza¸˜o, ´ dada por:
a ca ca e
x − xmin
ndcx = (1.11)
xmax − xmin
y − ymin
ndcy = (1.12)
ymax − ymin
Para visualizar dados num dispositivo gr´fico qualquer, ´ necess´rio transform´-los das coordenadas
a e a a
do usu´rio para NDCs, e de NDCs para coordenadas do dispositivo. Da mesma forma, dados de entrada
a
gr´ficos precisam ser transformados de coordenadas do dispositivo para NDCs, e depois para coordenadas
a
do usu´rio (Figura 1.3).
a
Figura 1.3: Sistemas de coordenadas e suas transforma¸˜es.
co
13

15. 1.6 Exerc´
ıcios
Escreva os procedimentos inp to ndc, ndc to user, user to ndc e ndc to dc, que transformam dados entre
os v´rios sistemas de coordenadas, conforme ilustrado na Figura 1.3. Repita o exerc´ assumindo que
a ıcio
o intervalo de varia¸˜o do sistema NDC vai de:
ca
(i) -1 a +1 (coordenadas normalizadas centradas)
(ii) 0 a 100
14

16. Cap´
ıtulo 2
Dispositivos de Visualiza¸˜o
ca
Toda imagem criada atrav´s de recursos computacionais deve ser representada em algum dispositivo f´
e ısico
que permita a sua visualiza¸˜o. Diversas tecnologias e diferentes tipos de dispositivos s˜o utilizados para
ca a
gerar representa¸˜es visuais, sendo que o desenvolvimento dessas tecnologias teve um papel fundamental
co
na evolu¸˜o da CG.
ca
Tanto para o usu´rio como para o implementador de sistemas gr´ficos ´ importante conhecer as
a a e
caracter´
ısticas de cada uma dessas tecnologias para sua melhor utiliza¸˜o. Vamos discutir alguns aspectos
ca
da arquitetura e organiza¸˜o dos tipos mais comuns dos dispositivos de exibi¸˜o gr´fica, sem entrar em
ca ca a
detalhes t´cnicos.
e
´
E poss´ ıvel classificar os dispositivos de exibi¸˜o (tra¸adores, impressoras e terminais de v´
ca c ıdeo) em
duas principais categorias, segundo a forma pela qual as imagens s˜o geradas: dispositivos vetoriais e
a
dispositivos matriciais. Os dispositivos gr´ficos vetoriais conseguem tra¸ar segmentos de reta perfeitos
a c
entre dois pontos da malha finita de pontos definida por suas superf´ ıcies de exibi¸˜o. Os dispositivos
ca
matriciais, por outro lado, apenas conseguem tra¸ar pontos, tamb´m em uma malha finita. Assim,
c e
segmentos de reta s˜o tra¸ados como sequˆncias de pontos pr´ximos.
a c e o
2.1 Dispositivos Gr´ficos Vetoriais
a
2.1.1 Tra¸adores Digitais
c
Tra¸adores (plotters) s˜o dispositivos eletromecˆnicos que produzem o desenho pelo movimento de
c a a
uma caneta sobre a superf´ do papel. A primitiva gr´fica b´sica nesse tipo de dispositivo ´ o segmento
ıcie a a e
de reta. Arcos, curvas e caracteres s˜o produzidos pelo tra¸ado de uma s´rie de pequenos segmentos.
a c e
Nos tra¸adores de mesa, o papel ´ fixado sobre uma superf´ plana retangular, sobre a qual est´ lo-
c e ıcie a
calizado um bra¸o mecˆnico que movimenta-se por transla¸˜o. Ao longo do bra¸o desloca-se um cabe¸ote
c a ca c c
que suporta uma caneta perpendicularmente ` mesa, a qual pode ser pressionada contra o papel ou
a
levantada de forma a n˜o toc´-lo.
a a
Nos tra¸adores de rolo, o bra¸o ´ fixo, e o papel ´ movimentado para frente e para tr´s por a¸˜o de
c c e e a ca
um rolo, como em uma m´quina de escrever.
a
Embora distintos em constru¸˜o, estes dois tipos de tra¸adores possuem caracter´
ca c ısticas de pro-
grama¸˜o e controle similares. A posic˜o da caneta sobre o papel ´ definida pelo posicionamento do
ca a e
bra¸o em rela¸˜o ao papel (abcissa x), e do cabe¸ote sobre o bra¸o (ordenada y). Figuras s˜o tra¸adas
c ca c c a c
pela varia¸˜o controlada da posi¸˜o da caneta (abcissa e ordenada) e pelo controle do estado da caneta
ca ca
(abaixada ou levantada). O tra¸ador ´ em geral controlado por um processador dedicado que recebe
c e
instru¸˜es diretamente do computador ou de um arquivo que descreve o desenho.
co
2.1.2 Dispositivos de V´
ıdeo Vetoriais (Vector Refresh Display Tubes)
No in´ da CG, o principal dispositivo de v´
ıcio ıdeo n˜o era um monitor parecido com uma TV, e sim um
a
car´
ıssimo CRT (Cathode Ray Tube) do tipo usado em oscilosc´pios. Como o display dos oscilosc´pios,
o o
os monitores tinham como entradas duas voltagens, x e y, que direcionavam um feixe de el´trons para
e
um ponto espec´ ıfico da tela. O feixe tra¸ava uma linha do ultimo ponto para o corrente, num unico
c ´ ´
movimento vetorial.
Um CRT consiste basicamente de uma superf´ de exibi¸˜o, quase plana, recoberta internamente
ıcie ca
de material ` base de f´sforo, um canh˜o emissor de el´trons e um sistema de deflex˜o (Figura 2.1). O
a o a e a
canh˜o emite um fino feixe de el´trons que, acelerados, chocam-se contra a superf´ fosforecente da tela.
a e ıcie
Sob a a¸˜o dos el´trons, o material fosforecente incandesce, emitindo luz no ponto da tela atingido pelo
ca e
15

17. Figura 2.1: Estrutura interna de um CRT.
feixe. A fun¸˜o do sistema de deflex˜o ´ dirigir controladamente o feixe de el´trons para um determinado
ca a e e
ponto da tela.
O brilho do f´sforo dura apenas alguns milisegundos (a emiss˜o de luz pelo f´sforo n˜o ´ est´vel, e
o a o a e a
cai a zero logo ap´s a interrup¸˜o do bombardeio de el´trons), de forma que toda a figura precisa ser
o ca e
continuamente retra¸ada para que o gr´fico permane¸a na tela. Este processo ´ denominado refreshing
c a c e
(da´ o nome, vector refreshing tubes). Se a imagem sendo mostrada ´ composta por muitos vetores, vai
ı e
haver um atraso significativo entre o tra¸ado do primeiro e do ultimo vetores, e alguns do vetores tra¸ados
c ´ c
inicialmente podem desaparecer nesse per´ ıodo. O resultado ´ que o tubo n˜o consegue retra¸ar a imagem
e a c
de modo suficientemente r´pido para evitar que um efeito de flickering (“cintila¸˜o”) torne-se aparente
a ca
na tela.
Figura 2.2: Convers˜o Digital-Anal´gica para Visualiza¸˜o num CRT.
a o ca
O tubo n˜o exige muita mem´ria para manter uma imagem complexa constru´ por segmentos de
a o ıda
reta, uma vez que apenas as coordenadas dos extremos dos segmentos, e as dos cantos da tela precisam
ser armazenadas. Esta era uma caracter´ ıstica importante no in´ da CG, j´ que a mem´ria era muito
ıcio a o
cara.
O computador gera as coordenadas dos pontos que definem a figura a ser mostrada na tela, e um
DAC (conversor digital-anal´gico) ´ necess´rio para converter os pontos digitais em voltagens a serem
o e a
enviadas para o CRT (Figura 2.2).
As desvantagens dos terminais gr´ficos vetoriais eram: a tecnologia cara, o efeito de flickering, e
a
a mem´ria limitada, que inviabilizava a descri¸˜o de imagens com detalhes complexos. As vantagens:
o ca
dispositivo gr´fico de alta resolu¸˜o (pelo menos 1000x1000), rapidez na gera¸˜o de imagens simples, o
a ca ca
que os torna adequados para testes iniciais em anima¸˜o.
ca
16

18. 2.1.3 Terminais CRT com mem´ria (Direct View Storage Tubes)
o
O CRT com mem´ria ´ um tubo especial que se comporta como se o f´sforo fosse de alt´
o e o ıssima persistˆncia.
e
Uma imagem tra¸ada nesse tipo de tubo pode manter-se por mais de uma hora sem sofrer desvanecimento.
c
Entretanto, o tubo ´ constru´ com f´sforo comum, e a longa persistˆncia da imagem ´ conseguida pela
e ıdo o e e
inclus˜o de dois elementos adicionais ao tubo: um canh˜o espalhador de el´trons e uma m´scara montada
a a e a
sobre a superf´ do f´sforo, entre a tela e os canh˜es.
ıcie o o
Os el´trons s˜o uniformemente espalhados por toda a superf´ da tela pelo canh˜o espalhador, e a
e a ıcie a
m´scara funciona como um filtro que seleciona os pontos ou ´reas da superf´ a serem atingidas pelos
a a ıcie
el´trons. Para isso, a m´scara ´ constru´ de material diel´trico pass´ de ser carregado de maneira n˜o
e a e ıda e ıvel a
uniforme. As ´reas carregadas positivamente atraem os el´trons, permitindo que passem pela m´scara.
a e a
Onde h´ carga negativa, os el´trons s˜o repelidos, e n˜o atingem o f´sforo.
a e a a o
Um canh˜o de el´trons ´ respons´vel pela emiss˜o de um feixe fino e intenso de el´trons que produz a
a e e a a e
carga diferenciada na m´scara. Dessa forma s˜o criados “buracos” na m´scara que deixar˜o os el´trons
a a a a e
do outro canh˜o passarem, definindo a forma da imagem a ser gerada. O desenho gravado na m´scara
a a
sustenta a imagem na tela at´ que uma voltagem positiva seja enviada para a m´scara, apagando a
e a
imagem.
Vantagens dos sistemas DVST: alta resolu¸˜o (pelo menos 1024x781); ausˆncia de flickering. Desvan-
ca e
tagens: n˜o h´ como apagar seletivamente a imagem. O apagamento da tela ´ sempre global, resultante
a a e
do carregamento uniforme da mascara; o apagamento causa um efeito de flashing na tela; a tecnologia
n˜o ´ adequada para monitores coloridos (usa apenas f´sforo verde); a imagem perde defini¸˜o com o
a e o ca
tempo; os tubos desgastam e precisam ser substitu´ ıdos.
A tecnologia dos DVST est´ ultrapassada, tendo sido substitu´ pelos dispositivos de varredura
a ıda
matriciais.
2.2 Primitivas de Software para Dispositivos Vetoriais
Uma primitiva de software ´ uma rotina ou um comando escrito em alguma linguagem que executa uma
e
fun¸˜o b´sica de um aplicativo: ou seja, uma primitiva de software implementa uma unica fun¸˜o. Um
ca a ´ ca
sistema de software complexo ´ constru´ atrav´s de chamadas hier´rquicas para suas fun¸˜es primitivas.
e ıdo e a co
Praticamente todos os dispositivos de sa´ vetoriais trabalham com duas primitivas de software
ıda
b´sicas: moveto(dcx,dcy) e drawto(dcx,dcy). A primeira move a posi¸˜o corrente (CP - current position)
a ca
do feixe (ou caneta, no caso de um plotter ) para o ponto definido pelas coordenadas do dispositivo
especificadas, (dcx, dcy), que passa a definir a nova CP. A segunda desenha um linha reta (ou, em outras
palavras, um vetor) entre o ponto definido pela CP e o ponto definido pelas coordenadas (dcx, dcy), que
passa a ser a nova CP.
Num sistema gr´fico com v´rios dispositivos de sa´ conectados ao computador hospedeiro, cada qual
a a ıda
com seu pr´prio sistema de coordenadas, ´ conveniente que o sistema disponha de primitivas gen´ricas
o e e
que sejam acessadas de maneira independente do dispositivo - atrav´s de NDCs ou de coordenadas f´
e ısicas.
As rotinas gen´ricas move to e draw to, nesse caso, cont´m estruturas “case” com comandos alternativos
e e
para cada dispositivo admitido, e enviam a sa´ para o dispositivo de sa´ correntemente ativado, depois
ıda ıda
de fazer as convers˜es apropriadas [Rankin, p. 29].
o
2.3 Dispositivos Gr´ficos Matriciais
a
2.3.1 Impressoras
Impressoras matriciais: nessas impressoras, os caracteres s˜o impressos por interm´dio de um conjunto
a e
de agulhas - um ponto ´ impresso quando uma agulha pressiona a fita sobre o papel. As agulhas s˜o
e a
montadas sobre um cabe¸ote m´vel, e os diferentes caracteres s˜o obtidos pelo acionamento conveniente
c o a
das agulhas a medida que o cabe¸ote se movimenta.
c
Estas impressoras podem operar no modo texto para a impress˜o de caracteres, ou num modo gr´fico
a a
(“bit image”) pelo qual ´ poss´ controlar cada agulha de modo independente. Em outras palavras, o
e ıvel
conjunto de padr˜es (caracteres) que podem ser impressos ´ program´vel. Cada padr˜o a ser impresso ´
o e a a e
definido por uma pequena matriz de pontos, onde cada ponto pode ser tra¸ado ou n˜o.
c a
Impressoras gr´ficas: Diversas t´cnicas tˆm sido utilizadas na constru¸˜o de impressoras gr´ficas,
a e e ca a
sendo que as mais comuns s˜o as tecnologias de jato de tinta e laser.
a
Nas impressoras a jato de tinta, o cabe¸ote transporta um pequeno bico que expele a tinta num jato
c
´
curto e fino sobre o papel. E poss´ ıvel variar a intensidade do jato, obtendo-se assim controle sobre a
17

19. densidade de impress˜o, e algumas impressoras disp˜em de v´rios bicos com tintas de cores diferentes,
a o a
cuja mistura produz diversas tonalidades.
Nas impressoras a laser, o processo de impress˜o ´ semelhante ao das copiadoras eletrost´ticas. Um
a e a
feixe de raio laser varre uma chapa numa trajet´ria semelhante ao de um cabe¸ote de uma impressora.
o c
O bombardeio do feixe deixa a chapa carregada com uma carga eletrost´tica n˜o uniforme. Por efeito da
a a
intensidade da carga, uma tintura (tonner ) adere ` chapa e por press˜o ´ impregnada no papel, formando
a a e
a imagem.
Apesar de utilizarem tecnologias distintas, estas impressoras produzem imagens de natureza seme-
lhante (mas com qualidade superior) `s geradas pelas impressoras matriciais em modo gr´fico. As imagens
a a
s˜o, em ultima instˆncia, constitu´
a ´ a ıdas de min´sculos pontos regularmente espa¸ados.
u c
2.3.2 Dispositivos de V´
ıdeo de Varredura (Raster Scanning VDUs)
A tecnologia utilizada atualmente na grande maioria dos terminais de v´
ıdeo gr´ficos ´ a mesma dos
a e
aparelhos de TV. Um terminal gr´fico simples requer (Figura 2.3):
a
Figura 2.3: Uma seq¨ˆncia de bits na mem´ria de imagem ´ convertida para uma seq¨ˆncia de pixels na
ue o e ue
tela.
Figura 2.4: Representa¸˜o esquem´tica de uma imagem matricial e sua representa¸˜o num frame buffer.
ca a ca
1. uma mem´ria digital (frame buffer, ou “mem´ria de imagem”), na qual a imagem a ser visualizada
o o
´ armazenada como uma matriz de pixels (cada posi¸˜o na matriz cont´m a intensidade associada
e ca e
ao pixel correspondente na tela) (Figura 2.4). Os dados da imagem s˜o colocados no frame buffer
a
pelo computador hospedeiro.
2. o monitor
3. um controlador de v´
ıdeo (display controller ), que consiste de uma interface que transfere o conte´do
u
do frame buffer para o monitor. Os dados devem ser transferidos repetidamente, pelo menos 15
vezes por segundo, de modo a manter uma imagem est´vel na tela, reduzindo o flickering. Note
a
que processo de transferˆncia implica numa convers˜o digital-anal´gica (DAC).
e a o
Para gerar a imagem, utiliza-se a t´cnica conhecida como raster scanning (“varredura”, ou “rastreio”),
e
que ´ a mesma utilizada na gera¸˜o de imagens de TV. Essa t´cnica tamb´m utiliza um CRT, sendo que
e ca e e
18

20. Figura 2.5: Varredura por rastreio fixo.
o feixe de el´trons varre a tela muitas vezes por segundo, de acordo com uma trajet´ria fixa (Figura 2.5).
e o
O feixe movimenta-se da esquerda para a direita, na horizontal. Ao final de uma varredura horizontal,
o feixe (com intensidade anulada) ´ reposicionado no in´
e ıcio da linha imediatamente abaixo, para nova
varredura.
Para garantir o “refrescamento” da imagem, o feixe ´ redirecionado ao ponto inicial da primeira linha
e
sempre que atingir o final da tela. Note que a intensidade do feixe num determinado pixel ´ determinada
e
pelo valor associado ao pixel no frame buffer. Se a mem´ria consiste de apenas um bit por pixel, ent˜o
o a
o pixel pode ter apenas dois estados: on ou off. Se existem oito bits por pixel, ent˜o cada pixel pode
a
variar entre 256 n´ıveis de intensidade, desde completamente off (preto), passando por diferentes n´ ıveis
de cinza, podendo chegar a completamente on (branco).
A dr´stica redu¸˜o dos custos de mem´ria de semicondutor, e o surgimento de circuitos integrados
a ca o
dedicados ao controle e ` gera¸˜o de sinais para terminais de rastreio fixo tornaram esta tecnologia
a ca
extremamente competitiva. Na tecnologia de varredura, todos os pontos que comp˜em uma imagem
o
precisam ser armazenados, e n˜o apenas os pontos extremos dos segmentos de reta. Consequentemente,
a
gr´ficos de varredura requerem muito mais mem´ria. Como o pre¸o da mem´ria digital est´ sendo
a o c o a
reduzido ` metade a cada ano que passa, a tecnologia tornou-se a alternativa mais acess´
a ıvel, utilizada
tanto em microcomputadores como em esta¸˜es de trabalho gr´ficas. Al´m do custo, outras vantagens
co a e
s˜o a capacidade de representar ´reas cheias, e n˜o somente linhas, e a possibilidade de utiliza¸˜o de
a a a ca
cores ou diferentes n´ıveis de cinza.
Figura 2.6: Representa¸˜o esquem´tica de um CRT por varredura colorido.
ca a
Em monitores monocrom´ticos, toda a superf´ da tela ´ revestida com o mesmo tipo de f´sforo, e
a ıcie e o
o feixe de el´trons pode ser direcionado para qualquer ponto da tela atrav´s das voltagens x e y. Num
e e
monitor colorido, cada pixel da tela ´ recoberto por trˆs tipos de f´sforo, que produzem as cores vermelho,
e e o
verde e azul (Red, Green, Blue - RGB). Ao inv´s de um unico feixe de el´trons existem trˆs, cada qual
e ´ e e
associado a uma cor de f´sforo. Entre a superf´ da tela recoberta de f´sforo, e os feixes de el´trons,
o ıcie o e
est´ uma barreira de metal, denominada shadow mask ou metal mask (Figura 2.6), que, por meio de
a
buracos em posi¸˜es estrat´gicas, garante que cada feixe atinge apenas o f´sforo ao qual est´ associado.
co e o a
19

21. R G B Valor Bin´rio
a Cor
0 0 0 0 preto
0 0 1 1 azul
0 1 0 2 verde
0 1 1 3 turquesa
1 0 0 4 vermelho
1 0 1 5 magenta
1 1 0 6 amarelo
1 1 1 7 branco
Tabela 2.1: Cores RGB em trˆs bits.
e
Variando a intensidade de cada feixe, varia-se a intensidade do brilho de cada f´sforo, obtendo-se cores
o
diferentes.
Assim como nos monitores monocrom´ticos o feixe de el´trons est´ associado a um conjunto de bits
a e a
na frame memory que determina a intensidade dos f´sforos vermelho, verde e azul. Se existe apenas um
o
bit associado a cada feixe (ou seja, trˆs bits de mem´ria por pixel), pode-se obter oito cores distintas,
e o
conforme mostrado na Tabela 2.1. O n´mero de bits associado a cada pixel ´ denominado pixel depth
u e
(bit planes), ou “profundidade” do pixel.
Se cada feixe tem profundidade p, o pixel tem profundidade 3p, e pode-se gerar 23p cores. Alguns
terminais gr´ficos tˆm pixels com profundidade quatro, sendo que os trˆs primeiros bits correspondem
a e e
aos valores R, G e B, e o quarto especifica o brilho, ou intensidade total da cor mostrada. Isto resulta
em 24 = 16 cores poss´ ıveis para cada pixel. Outros sistemas usam valores diferentes de profundidade de
pixel, com significados diferentes associados aos respectivos bit planes.
Se a profundidade do pixel ´ D, o n´mero real de cores poss´
e u ıveis ´ 2D , mas o n´mero total de cores
e u
que podem ser mostradas, denominado palette range, pode ser bem maior. Ao inv´s de usar o valor do
e
pixel armazenado na mem´ria para controlar o feixe diretamente (e.g., us´-lo como uma cor), ele ´ usado
o a e
como um ´ ındice para uma tabela de cores (color lookup table, CLUT). Um palette, ou “cor l´gica”, ´ um
o e
dos 2D valores de pixel poss´ ıveis, e portanto existem 2D palettes (0 a 2D − 1). Um software pode atribuir
valores associados a cores f´
ısicas `s posi¸˜es da look-up table correspondentes a um palette. Assim, o valor
a co
armazenado numa posi¸˜o da tabela ´ usado para controlar a cor do pixel associado no monitor.
ca e
Figura 2.7: Organiza¸˜o de uma v´
ca ıdeo look-up table.
Em geral, a tabela de cores ´ uma area fixa de RAM com 2D posi¸˜es de 24 bits cada: a cada feixe
e ´ co
(ou cor) s˜o associados 8 bits, e portanto cada feixe pode ter 256 n´
a ıveis de intensidade. Isto resulta num
total de 16 milh˜es de cores poss´
o ıveis, sendo que apenas 2D podem ser mostradas simultaneamente na
tela. A Figura 2.7 mostra um frame buffer com 8 bits por pixel, e uma LUT com 12 bits por posi¸˜o. ca
2.3.3 Primitivas de Software
A primitiva b´sica, no caso de um dispositivo matricial, tra¸a um ponto numa determinada posi¸˜o do
a c ca
retˆngulo de visualiza¸˜o:
a ca
int write_pixel(int dcx, int dcy, int pixel_value)
Tamb´m ´ poss´ ler dados de um dispositivo, atrav´s da primitiva inversa:
e e ıvel e
int read_pixel(int dcx, int dcy, int *pixel_value)
20

22. Em ambos os casos, os dados s˜o lidos ou escritos no frame buffer, ou mem´ria de imagem, que
a o
armazena todos os pixels de uma imagem a ser visualizada ou lida. Al´m disso, o programador precisa
e
acessar a lookup table - caso ela exista - o que ´ feito atrav´s de duas primitivas:
e e
int write_CLUT(int pixel_value,int R, int G, int B)
read_CLUT(int pixel_value, int *R, int *G, int *B)
Todos os comandos gr´ficos num sistema envolvendo dispositivos matriciais podem ser constru´
a ıdos a
partir dessas quatro primitivas.
Num sistema b´sico com um dispositivo de visualiza¸˜o monocrom´tico, as primitivas podem ser
a ca a
reduzidas simplesmente a duas rotinas b´sicas, que s˜o casos especiais da rotina “write pixel”. Estas
a a
rotinas “acendem” e “apagam” o ponto definido pelas coordenadas (dcx, dcy).
dot_on(int dcx, int dcy);
dot_off(int dcx, int dcy)
Apesar destas subrotinas usarem coordenadas de tela, rotinas num n´ ıvel superior executariam as
transformadas de visualiza¸˜o para converter coordenadas do usu´rio para coordenadas do dispositivo.
ca a
2.4 Exerc´
ıcios
1. Escreva um programa (em C) que desenhe um pol´ ıgono regular (ou seja, um pol´ıgono com lados de
comprimentos iguais e ˆngulos internos iguais) com raio igual a um ter¸o da altura da tela, e centro no
a c
centro da tela. O programa deve solicitar o n´mero de v´rtices, n.
u e
2. Modifique o programa do exerc´ anterior para solicitar tamb´m o raio r do c´
ıcio e ırculo que circunscreve
o pol´
ıgono. Fa¸a com que o seu programa estime o n´mero n de v´rtices necess´rios para que o pol´
c u e a ıgono
pare¸a uma “boa aproxima¸˜o” para um c´
c ca ırculo, para diferentes raios. Usando os parˆmetros ndh, ndv,
a
width, height do dispositivo, obtenha uma rela¸˜o te´rica entre n e r para a aproxima¸˜o de c´
ca o ca ırculos
atrav´s de pol´
e ıgonos.
3. Alguns dispositivos vetoriais oferecem um conjunto de trˆs primitivas gr´ficas:
e a
• pen up: levanta a caneta do papel, ou desliga o feixe de el´trons;
e
• pen down: coloca a caneta sobre o papel, ou liga o feixe;
• locate(dcx,dcy): posiciona a CP num ponto do retˆngulo de visualiza¸˜o.
a ca
Escreva rotinas de software que simulem estas trˆs primitivas, usando as primitivas moveto e drawto.
e
4. Calcule as raz˜es de aspecto (gr´fica e f´
o a ısica), e as resolu¸˜es de ´rea horizontal e vertical de uma tela
co a
de TV colorida padr˜o, onde:
a
• width = 42cm;
• height = 31cm;
• ndh = 546;
• ndv = 434.
2.5 Dispositivos de Entrada
Juntamente com os dispositivos de sa´ıda, os dispositivos de entrada gr´fica permitem o estabelecimento
a
a a ´
da comunica¸˜o usu´rio-m´quina. E importante que programadores de sistemas e aplicativos gr´ficos
ca a
compreendam a natureza dos principais dispositivos de entrada, de forma a selecion´-los adequadamente
a
em fun¸˜o da natureza das informa¸˜es a serem tratadas, e da maior ou menor facilidade que oferecem
ca co
aos usu´rios para exprimir informa¸˜es.
a co
21

23. 2.5.1 Teclado
O teclado alfanum´rico ´ o recurso mais utilizado na comunica¸˜o entre usu´rio e m´quina, permitindo
e e ca a a
a entrada de textos e dados num´ricos. Um teclado alfanum´rico estendido inclui teclas adicionais para
e e
a sele¸˜o de alternativas em menus ou para o disparo de fun¸˜es espec´
ca co ıficas. Teclas de movimento de
cursor podem ser usadas para sele¸˜o de coordenadas de um ponto em uma tela gr´fica.
ca a
Em geral, valores de coordenadas especificando posi¸˜es de um cursor na tela s˜o fornecidas para o
co a
computador por meio de dispositivos como a ligth pen, o joystick, o mouse e as mesas digitalizadoras
(tablets).
2.5.2 Ligth Pen
´
E um dispositivo que funciona associado a um monitor de v´ ıdeo, e que ´ capaz de detectar luz. A caneta
e
tem em sua ponta uma c´lula fotoel´trica e um interruptor de press˜o. Ao ser pressionado contra a tela,
e e a
o interruptor habilita a c´lula a detectar o pulso de luz emitido pelos f´sforos que recobrem a tela no
e o
ponto sendo apontado.
Quando a ligth pen detecta um pulso de luz num terminal de varredura, o conte´do dos registradores
u
X e Y do controlador de v´ ıdeo ´ armazenado, e o processamento ´ interrompido. Atrav´s dos valores
e e e
armazenados, o software gr´fico determina as coordenadas do pixel apontado pela caneta.
a
Quando detecta um pulso de luz num monitor vetorial, a caneta informa ao processador, a execu¸˜o ca
´ interrompida, e o processador ´ capaz de detectar qual instru¸˜o de tra¸ado estava em execu¸˜o no
e e ca c ca
momento que ocorreu a interrup¸˜o, e portanto qual segmento de reta foi apontado pelo operador. A
ca
caneta ´ uma tecnologia um tanto ultrapassada, por ser cansativa para o usu´rio e sujeita a falhas.
e a
2.5.3 Joystick
´
E uma alavanca que admite movimentos para frente e para tr´s, esquerda e direita. Dois potenciˆmetros
a o
s˜o respons´veis pela detec¸˜o dos movimentos na horizontal e na vertical. Sua manipula¸˜o fornece um
a a ca ca
e ca ´
par de valores num´ricos em uma faixa limitada fixa para cada posi¸˜o da alavanca. E um dispositivo de
baixo custo, bastante utilizado em microcomputadores. Entretanto, o joystick ´ um dispositivo de baixa
e
resolu¸˜o, e n˜o ´ muito adequado para controlar a posi¸˜o absoluta de um cursor na tela.
ca a e ca
2.5.4 Mouse
O mouse ´ uma pequena caixa que pode deslizar sobre uma superf´ plana. Na parte inferior, uma
e ıcie
pequena esfera incrustada no mouse rola livremente a medida que este se movimenta. Os movimentos
de rota¸˜o da esfera relativos ` caixa s˜o transmitidos mecanicamente a dois potenciˆmetros que medem
ca a a o
o deslocamento do mouse em rela¸˜o a dois eixos ortogonais fixos. Como o sistema de eixos ´ fixo em
ca e
rela¸˜o ` caixa, o dispositivo ´ capaz apenas de detectar movimentos relativos ` sua pr´pria posi¸˜o
ca a e a o ca
atual. Ele pode ser levantado da superf´ ıcie, movido e colocado de volta sobre a superf´ sem que a sua
ıcie
posi¸˜o corrente no sistema seja alterada.
ca
2.5.5 Mesa Digitalizadora (Tablet)
´
E o dispositivo mais adequado para entrada de dados geom´tricos. Consiste de uma superf´ plana e
e ıcie
um cursor que pode ser posicionado sobre a superf´ ıcie. Por indu¸˜o eletromagn´tica, a posi¸˜o corrente
ca e ca
do cursor, relativa a um referencial fixo ` mesa, pode ser detectada e transmitida ao processador.
a
2.5.6 Data Glove
´
E o dispositivo de entrada e sa´ pelas m˜os utilizado em realidade virtual. Consiste de um conjunto
ıda a
de sensores acoplados a uma luva que detectam movimento e for¸a dos dedos. Antenas de transmiss˜o
c a
e recep¸˜o s˜o respons´veis por fornecer posicionamento das m˜os. Com isso, a posi¸˜o das m˜os pode
ca a a a ca a
indicar posi¸˜o de objetos, que s˜o ent˜o mapeados para tela ou para um dispositivo de headtrack.
ca a a
2.5.7 Outros dispositivos
Entrada por voz, som via MIDI.
22

24. Cap´
ıtulo 3
Tra¸ado de Curvas em Dispositivos
c
Gr´ficos Matriciais
a
O tra¸ado de primitivas gr´ficas elementares, como segmentos de reta ou arcos de circunferˆncia, requer a
c a e
constru¸˜o de algoritmos capazes de determinar na matriz de pixels da superf´ de exibi¸˜o quais pixels
ca ıcie ca
devem ser alterados de forma a simular-se a aparˆncia do elemento gr´fico desejado. Estes algoritmos
e a
recebem o nome de Algoritmos de Convers˜o Matricial, por converterem em representa¸˜o matricial
a ca
elementos gr´ficos expressos em uma representa¸˜o vetorial.
a ca
Um elemento geom´trico b´sico a ser tra¸ado num terminal gr´fico ´ o segmento de reta. Atualmente,
e a c a e
´ comum que rotinas de tra¸ado de linhas estejam dispon´
e c ıveis em hardware (em chips controladores).
O chip recebe as coordenadas dos pixels extremos, e calcula quais pixels intermedi´rios da superf´ de
a ıcie
exibi¸˜o devem ser tra¸ados para gerar uma reta (aproximada) na tela.
ca c
Gr´ficos complexos requerem o tra¸ado de uma grande quantidade de segmentos de reta, e a velocidade
a c
´ importante - da´ a op¸˜o de tra¸ado por meio de hardware especializado, que libera o processador
e ı ca c
hospedeiro para outras atividades enquanto o chip controlador calcula os pixels a serem tra¸ados.
c
Se a fun¸˜o de tra¸ado precisa ser implementada em software, a rotina deve ser escrita em c´digo
ca c o
de m´quina otimizado para atingir o m´ximo de velocidade. Entretanto, ´ instrutivo estudar alguns
a a e
algoritmos para tra¸ado de linhas usando uma linguagem de alto n´
c ıvel.
Suponhamos, que a superf´ de exibi¸˜o possua igual densidade de pixels na horizontal e na vertical
ıcie ca
(raz˜o de aspecto gr´fica igual a 1).
a a
A seguir ser´ apresentada uma importante propriedade do espa¸o onde os diversos elementos gr´ficos
a c a
ser˜o tra¸ados.
a c
Figura 3.1: Representa¸˜o de segmentos de reta horizontais, verticais e diagonais.
ca
23

25. Figura 3.2: Reflex˜o de uma imagem com rela¸˜o a um eixo diagonal.
a ca
Figura 3.3: Rota¸˜o de 90o obtida atrav´s de 2 reflex˜es, uma horizontal (a) e outra na diagonal (b).
ca e o
3.1 Simetria e Reflex˜o
a
Tomemos como exemplo o tra¸ado de um segmento de reta. A representa¸˜o matricial de segmentos de
c ca
reta horizontais, verticais, e diagonais a 45 e 135 n˜o apresenta nenhuma dificuldade (ver Figura 3.1).
a
Pode-se dizer que estas dire¸˜es formam na realidade eixos de simetria no espa¸o matricial. Logo, qualquer
co c
imagem representada no espa¸o matricial pode ser refletida em rela¸˜o a qualquer reta horizontal, vertical
c ca
ou diagonal sem apresentar qualquer deforma¸˜o (ver Figura 3.2).
ca
A Simetria ser´ explorada na convers˜o matricial de primitivas gr´ficas que apresentem simetria em
a a a
rela¸˜o a qualquer um destes eixos. Na Figura 3.3 pode-se ver como efetuar a rota¸˜o de uma imagem
ca ca
utilizando de 2 reflex˜es.
o
3.2 Convers˜o Matricial de Segmentos de Reta
a
Alguns crit´rios de convers˜o matricial podem ser vistos atrav´s da Figura 3.4.
e a e
Em (a) adotou-se o crit´rio de selecionar-se os dois pixels imediatamente acima e abaixo do ponto de
e
intersec¸˜o do segmento com cada vertical, a menos quando o segmento passa por um pixel. Restri¸˜o:
ca ca
dessa forma obt´m-se linhas densas, como se o segmento fosse espesso.
e
Em (b) o crit´rio foi selecionar todos os pixels cujas coordenadas s˜o obtidas arredondando-se os
e a
valores das coordenadas de algum ponto do segmento. Restri¸˜o: com segmentos a 45 o crit´rio produz
ca e
resultados semelhantes ao anterior.
A convers˜o ilustrada em (c) foi obtida selecionando-se em cada vertical o pixel mais pr´ximo do
a o
ponto de intersec¸˜o do segmento com a reta vertical. Vantagens: aparˆncia leve e continuidade.
ca e
Em (d) utilizou-se o mesmo crit´rio, s´ que para as linhas horizontais. Restri¸˜o: descontinuidade.
e o ca
24

26. Figura 3.4: Convers˜es matriciais de um segmento de reta resultante de diferentes crit´rios.
o e
3.2.1 Caracter´
ısticas Desej´veis para os Algoritmos de convers˜o Matricial
a a
de Segmentos de Retas
1. Linearidade: os pixels tra¸ados devem dar a aparˆncia de que est˜o sobre uma reta. Isto ´ trivial
c e a e
no caso de segmentos paralelos aos eixos x ou y, ou com inclina¸˜o de 45 graus, mas n˜o nos outros
ca a
casos.
2. Precis˜o: os segmentos devem iniciar e terminar nos pontos especificados. Caso isso n˜o ocorra,
a a
pequenos gaps podem surgir entre o final de um segmento e o in´ de outro.
ıcio
3. Espessura (Densidade) uniforme: a densidade da linha ´ dada pelo n´mero de pixels tra¸ados
e u c
dividido pelo comprimento da linha. Para manter a densidade constante, os pixels devem ser
igualmente espa¸ados. A imagem do segmento n˜o varia de intensidade ou espessura ao longo de
c a
sua extens˜o.
a
4. Intensidade independente da inclina¸˜o: para segmentos de diferentes inclina¸˜es
ca co
5. Continuidade: a imagem n˜o apresenta interrup¸˜es indesej´veis.
a co a
6. Rapidez no Tra¸ado dos segmentos.
c
Os algoritmos que vamos estudar usam o m´todo incremental, que consiste em executar os c´lculos
e a
iterativamente, mantendo um registro (ou mem´ria) do progresso da computa¸˜o a cada passo da itera¸˜o.
o ca ca
Nesse m´todo, come¸ando por um dos extremos da linha, o pr´ximo ponto ´ calculado e tra¸ado at´ que
e c o e c e
o outro extremo seja atingido e tra¸ado.
c
O problema da convers˜o matricial consiste essencialmente em ajustar uma curva, no caso, um seg-
a
mento de reta, a qual ´ precisamente definida por coordenadas reais, a uma malha de coordenadas
e
inteiras. Isto pode ser feito calculando as coordenadas reais, (xr , yr ), do pr´ximo ponto na linha, e es-
o
colhendo na malha os pixels cujas coordenadas (x, y) mais se aproximam das coordenadas reais, obtidos
por arredondamento ou truncamento.
Qualquer algoritmo de tra¸ado de linhas pode ser testado com rela¸˜o aos requisitos acima: Para
c ca
o requisito 1, calcula-se a soma dos quadrados das diferen¸as entre cada par (xr , yr ), (x, y). O melhor
c
algoritmo ´ o que resultar na menor diferen¸a. O requisito 2 ´ problem´tico apenas quando os pontos
e c e a
extremos dos segmentos s˜o especificados em coordenadas do usu´rio. Para o requisito 3, conta-se o
a a
n´mero de pixels tra¸ados, e divide-se pelo comprimento da linha. Os requisitos 4 e 6 s˜o avaliados
u c a
atrav´s da execu¸˜o de benchmarks em cada algoritmo, para efeito de compara¸˜o. O requisito 5 pode
e ca ca
ser verificado analisando-se os tamanho dos “buracos” entre um ponto e o seu pr´ximo, o que pode ser
o
feito atrav´s de um algoritmo que calcule a distˆncia entre dois pontos.
e a
3.2.2 Crit´rio Adotado
e
Seja o segmento de reta definido por seus extremos (x1 , y1 ) e (x2 , y2 ).
Pode-se supor que este segmento est´ no 1o octante (porquˆ?!). Ent˜o estas coordenadas respeitam as
a e a
rela¸˜es:
co
25

27. 0 < x1 < x2 (3.1)
0 < y1 < y2 (3.2)
y2 − y1 < x2 − x1 (3.3)
Nestas condi¸˜es o segmento de reta corta um n´mero maior de linhas verticais do reticulado do que
co u
de horizontais e assim:
Crit´rio de Convers˜o: em cada vertical do retilado com abscissa entre x1 e x2 apenas o
e a
pixel mais pr´ximo da interse¸˜o do segmento com a vertical faz parte da sua imagem.
o ca
Este crit´rio aplicado a segmentos do 2o octante n˜o produz resultados satisfat´rios (tente fazˆ-lo!),
e a o e
pois nesse caso o n´mero de verticais que corta o segmento ser´ menor que o de horizontais. Solu¸˜o:
u a ca
para segmentos no 2o octante utilizar este crit´rio s´ que trocando x com y e vertical por horizontal. A
e o
Figura 3.5 apresenta a convers˜o de segmentos pelo crit´rio acima.
a e
Figura 3.5: Imagens de segmentos de reta convertidos pelo crit´rio expl´
e ıcito acima.
3.2.3 Algoritmos
Equa¸˜o da reta:
ca
y = y1 + a(x − x1 ) (3.4)
(y2 −y1 )
onde a = (x2 −x1 ) .
Dessa forma, basta que para cada vertical da grade entre x1 e x2 , determinemos o inteiro mais pr´ximo
o
da ordenada correspondente da reta. O algoritmo 3.1 implementa esta id´ia. e
3.2.4 Algoritmo do “Ponto-M´dio”
e
Um algoritmo equivalente a este mas que dispensa as opera¸˜es em ponto flutuante foi proposto por
co
Bresenham (em 1965). Bresenham desenvolveu um algoritmo cl´ssico que usa apenas vari´veis inteiras,
a a
e que permite que o c´lculo de (xi + 1, yi + 1) seja feito incrementalmente, usando os c´lculos j´ feitos
a a a
para (xi , yi ). Vamos estudar uma vers˜o do Algoritmo de Bresenham denominada MidPoint Line
a
Algorithm (“Algoritmo do Ponto-M´dio ou Meio-Ponto para Retas”) por Foley.
e
O algoritmo assume que a inclina¸˜o da linha est´ entre 0 e 1 (outras inclina¸˜es podem ser tratadas
ca a co
por simetria). O ponto (x1 , y1 ) ´ o inferior esquerdo, e (x2 , y2 ) ´ o superior direito.
e e
Considere a linha na Figura 3.6. Assumindo que o pixel que acabou de ser selecionado ´ P , em e
(xp , yp ), e o pr´ximo deve ser escolhido entre o pixel ` direita (pixel E) e o pixel acima ` direita (NE).
o a a
Seja Q o ponto de intersec¸˜o entre a reta e a coluna x = xp + 1 da malha, e M o ponto intermedi´rio
ca a
entre os pixels E e NE. O que se faz ´ observar de que lado da reta est´ o ponto M . E a
e a ´ f´cil verificar que
se M est´ acima da reta, o pixel E est´ mais pr´ximo da reta; se M est´ abaixo, NE est´ mais pr´ximo.
a a o a a o
26

28. void line(int x1, int y1, int x2, int y2, int color){
int x, y;
float a;
int valor;
a=(y2-y1)/(x2-x1);
for (x=x1;x<=x2;x++){
/* arredonda y */
y = (y1 + a * (x - x1));
write_pixel(x, y, color);
}/* end for */
}/*end line */
´
Algoritmo 3.1: Algoritmo simples para convers˜o matricial de retas. E pouco eficiente pois
a
utiliza c´lculos de ponto flutuante.
a
Figura 3.6: Grade de pixels para o Algoritimo o Ponto-M´dio (M) e as escolhas E e NE.
e
27

29. Dessa forma, o teste do ponto-m´dio permite a escolha do pixel mais pr´ximo da reta. Al´m disso, o erro
e o e
(a distˆncia vertical entre o pixel escolhido e a linha) ´ sempre ≤ 1 .
a e 2
O que precisamos agora ´ um m´todo para calcular de que lado da reta est´ o ponto M . Para isso,
e e a
considere sua fun¸˜o impl´
ca ıcita, F (x, y) = ax + by + c = 0. Se dy = y2 − y1 , e dx = x2 − x1 , a equa¸˜o da
ca
reta em termos de sua inclina¸˜o pode ser escrita como:
ca
dy
y= x+B (3.5)
dx
e, consequentemente,
F (x, y) = dy.x − dx.y + B.dx = 0 (3.6)
Aqui, tem-se a = dy, b = −dx, e c = B.dx.
´ a
E f´cil verificar que F (x, y) = 0 sobre a linha, positiva para pontos abaixo dela, e negativa para
1
pontos acima dela. Para o teste do ponto-m´dio, basta calcular F (M ) = F (xp + 1, yp + 2 ) e verificar o
e
seu sinal. Como a decis˜o ser´ tomada com base no valor da fun¸˜o no ponto (xp + 1, yp + 1 ), definimos
a a ca 2
uma “vari´vel de decis˜o” d = a(xp + 1) + b(yp + 1 ) + c. Se d > 0, escolhemos o pixel NE, se d < 0,
a a 2
escolhemos o pixel E; se d = 0 pode-se escolher qualquer um deles, por exemplo E.
´
E interessante verificar o que acontece com a localiza¸˜o de M e o valor de d no pr´ximo ponto da
ca o
reta. Ambos dependem, obviamente, da escolha de E ou NE. Se E for escolhido, M ´ incrementado de 1
e
na dire¸˜o x. Assim,
ca
1 1
dnew = F (xp + 2, yp + ) = a(xp + 2) + b(yp + ) + c (3.7)
2 2
mas
1
dold = a(xp + 1) + b(yp + ) + c (3.8)
2
Subtraindo dold de dnew para obter a diferen¸a incremental, tem-se dnew = dold + a.
c
Denominamos ∆E o incremento a ser adicionado depois da escolha de E; e ∆E = a = dy. Em outras
palavras, pode-se derivar o valor da vari´vel de decis˜o no pr´ximo passo incrementalmente, a partir do
a a o
seu valor atual, sem necessidade de calcular F (M ) diretamente.
Se NE ´ escolhido, M ´ incrementado de 1 em ambas as dire¸˜es, x e y. Portanto,
e e co
Subtraindo dold de dnew , tem-se dnew = dold +a+b. Denominamos ∆N E o incremento a ser adicionado
depois da escolha de NE; e ∆N E = a + b = dy − dx.
Resumindo a t´cnica incremental do ponto-m´dio
e e
A cada passo, o algoritmo escolhe entre 2 pixels, com base no sinal da vari´vel de decis˜o calculada
a a
na itera¸˜o anterior; a seguir a vari´vel de decis˜o ´ atualizada adicionando-se ∆E ou ∆N E ao valor
ca a a e
anterior, dependendo do pixel escolhido.
Como o primeiro pixel corresponde ao ponto (x1 , y1 ), pode-se calcular diretamente o valor inicial de
1
d para escolher entre E e NE. O primeiro ponto-m´dio est´ em (x1 + 1, y1 + 2 ), e
e a
1 1 b b
F (x1 + 1, y1 + ) = a(x1 + 1) + b(y1 + ) + c = ax1 + by1 + c + a + = F (x1 , y1 ) + a + (3.9)
2 2 2 2
Como (x1 , y1 ) ´ um ponto da reta, F (x1 , y1 ) ´ 0; consequentemente dstart ´ dado por a + 2 = dy − dx .
e e e b
2
Usando dstart, escolhe-se o segundo pixel, e assim por diante. Para eliminar a fra¸˜o em dstart , F ´
ca e
multiplicada por 2. Isto ´:
e
F (x, y) = 2(ax + by + c). Isto multiplica cada constante e a vari´vel de decis˜o por 2, mas n˜o afeta o
a a a
sinal da vari´vel de decis˜o, que ´ o que interessa para o teste do ponto-m´dio.
a a e e
A aritm´tica necess´ria para calcular dnew a cada passo ´ adi¸˜o simples - nenhuma multiplica¸˜o ´
e a e ca ca e
necess´ria (veja o algoritmo abaixo). Note que esta vers˜o do algoritmo funciona apenas para linhas com
a a
inclina¸˜o entre 0 e 1, mas a generaliza¸˜o n˜o ´ dif´
ca ca a e ıcil. A Figura 3.7 mostra a reta que vai do ponto
(5,8) ao ponto (9,11), tra¸ada por este algoritmo. Os valores sucessivos de d s˜o 2, 0, 6 e 4, resultantes
c a
da escolha de NE, E, NE e NE, respectivamente.
Exerc´ıcios
1. Escreva procedimentos para checar os 6 requisitos de um bom algoritmo de convers˜o matricial, e
a
aplique-os aos algoritmos de convers˜o estudados.
a
2. Escreva uma vers˜o melhorada do Algoritmo de Bresenham, que teste se as itera¸˜es devem ser
a co
feitas ao longo do eixo x ou ao longo do eixo y, e tamb´m para checar exce¸˜es como linhas paralelas
e co
ao eixo x.
28

30. Figura 3.7: Grade de pixels para o Algoritimo o Ponto-M´dio (M) e as escolhas E e NE.
e
3.3 Convers˜o Matricial de Circunferˆncias
a e
A equa¸˜o de uma circunferˆncia com centro na origem e raio R, em coordenadas cartesianas, ´ dada
ca e e
por:
x2 + y 2 = R2 (3.10)
Circunferˆncias n˜o centradas na origem podem ser transladadas para a origem, e os pixels reais
e a
podem ser tra¸ados aplicando-se um offset aos pixels gerados pelo algoritmo de convers˜o matricial.
c a
Existem muitas abordagens simples, por´m ineficientes, para o tra¸ado de c´
e c ırculos: Em algoritmos
n˜o incrementais, um pol´
a ıgono regular de n lados ´ usado como aproxima¸˜o para a circunferˆncia. Para
e ca e
que a aproxima¸˜o seja razo´vel, deve-se escolher um valor suficientemente alto para n. Entretanto,
ca a
quanto maior o valor de n, mais lento ser´ o algoritmo, e v´rias estrat´gias de acelera¸˜o precisam ser
a a e ca
usadas. Em geral os algoritmos incrementais de convers˜o matricial s˜o mais r´pidos.
a a a
Outra abordagem seria usar a equa¸˜o expl´
ca ıcita da circunferˆncia, y = f (x):
e
y = ± R2 − x2 (3.11)
1
Figura 3.8: Um arco de 4 de circunferˆncia, obtido variando-se x em incrementos unit´rios, e calculando
e a
e arrendondando y.
Para desenhar 1 de circunferˆncia (os outros 3 s˜o desenhados por simetria), poder´
4 e 4 a ıamos variar x de
0 a R, em incrementos de uma unidade, calculando +y a cada passo atrav´s da equa¸˜o acima. Essa
e ca
estrat´gia funciona, mas ´ ineficiente porque requer opera¸˜es de multiplica¸˜o e raiz quadrada. Al´m
e e co ca e
29

31. void inc_line(int x1, int y1, int x2, int y2, int color){
int dx, dy, incE, incNE, d, x, y;
dx = x2 - x1;
dy = y2 - y1;
d = 2 * dy - dx; /* Valor inicial de d */
incE = 2 * dy; /* Incremento de E */
incNE = 2 * (dy - dx); /* Incremento de NE */
x = x1;
y = y1;
write_pixel(x, y, color);
while (x < x2){
if (d <= 0){
/* Escolhe E */
d = d + incE;
x = x + 1;
}else{
/* Escolhe NE */
d = d + incNE;
x = x + 1;
y = y + 1;
}/* end if */
write_pixel(x, y, color);
}/* end while */
}/* end inc_line */
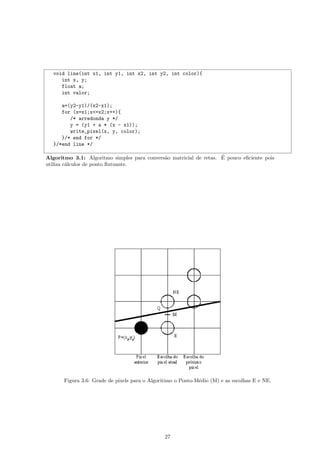
Algoritmo 3.2: Algoritmo do Ponto-M´dio incremental.
e
disso, haver´ grandes gaps nas regi˜es onde a tangente ` circunferˆncia ´ infinita (valores de x pr´ximos
a o a e e o
a R, Figura 3.8). Uma maneira de resolver o problema dos gaps ´ “plotar” x = R. cos θ e y = R. sin θ,
e
para variando de 0 a 90 graus, mas essa solu¸˜o tamb´m ´ ineficiente, pois precisa de fun¸˜es caras (sin
ca e e co
e cos).
3.3.1 Simetria de ordem 8
Note que o tra¸ado de uma circunferˆncia pode tirar proveito de sua simetria. Considere uma circun-
c e
ferˆncia centrada na origem. Se o ponto (x, y) pertence ` circunferˆncia, pode-se calcular de maneira
e a e
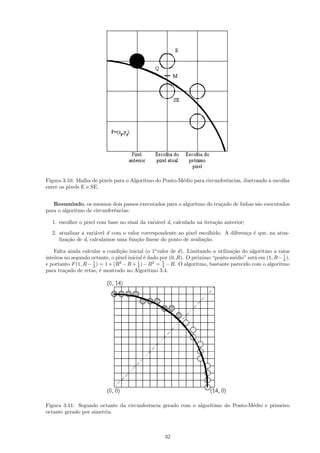
trivial sete outros pontos da circunferˆncia (Figura 3.9). Consequentemente, basta computar um arco de
e
circunferˆncia de 45o para obter a circunferˆncia toda. Para uma circunferˆncia com centro na origem, os
e e e
oito pontos sim´tricos podem ser tra¸ados usando o procedimento CirclePoints (Algoritmo 3.3).
e c
void CirclePoints(int x, int y, int color){
write_pixel( x, y, color);
write_pixel( x, -y, color);
write_pixel(-x, y, color);
write_pixel(-x, -y, color);
write_pixel( y, x, color);
write_pixel( y, -x, color);
write_pixel(-y, x, color);
write_pixel(-y, -x, color);
}/* end CirclePoints */
Algoritmo 3.3: Procedimento CirclePoints.
Vamos estudar especificamente um algoritmo derivado do algoritmo de Bresenham para gera¸˜o de
ca
circunferˆncias, chamado “Midpoint Circle Algorithm” em [Foley et. al].
e
30

32. Figura 3.9: Oito pontos sim´tricos em uma circunferˆncia.
e e
3.3.2 Algoritmo do “Ponto-M´dio” para Circunferˆncias
e e
R
Consideraremos apenas um arco de 45o da circunferˆncia, o 2o octante, de x = 0, y = R a x = y = √2 ,
e
e usaremos o procedimento CirclePoints para tra¸ar todos os pontos da circunferˆncia. Assim como o
c e
algoritmo gerador de linhas, a estrat´gia ´ selecionar entre 2 pixels na malha aquele que est´ mais pr´ximo
e e a o
da circunferˆncia, avaliando-se uma fun¸˜o no ponto intermedi´rio entre os dois pixels. No segundo
e ca a
octante, se o pixel P em (xp , yp ) foi previamente escolhido como o mais pr´ximo da circunferˆncia, a
o e
escolha do pr´ximo pixel ser´ entre os pixels E e SE (Figure 3.10).
o a
Seja a fun¸˜o F (x, y) = x2 +y 2 −R2 , cujo valor ´ 0 sobre a circunferˆncia, positivo fora dela e negativo
ca e e
dentro. Se o ponto intermedi´rio (o “ponto-m´dio”) entre os pixels E e SE est´ fora da circunferˆncia, o
a e a e
pixel SE ´ escolhido, porque est´ mais pr´ximo dela. Por outro lado, se o pixel intermedi´rio est´ dentro
e a o a a
da circunferˆncia, ent˜o o pixel E ´ escolhido.
e a e
Assim como no caso das linhas, a escolha ´ feita com base na vari´vel de decis˜o d, que d´ o valor da
e a a a
fun¸˜o no “ponto-m´dio”:
ca e
1 1
dold = F (xp + 1, yp − ) = (xp + 1)2 + (yp − )2 − R2 (3.12)
2 2
Se dold < 0, E ´ escolhido, e o pr´ximo ponto-m´dio ser´ incrementado de 1 na dire¸˜o x. Assim,
e o e a ca
1 1
dnew = F (xp + 2, yp − ) = (xp + 2)2 + (yp − )2 − R2 (3.13)
2 2
e dnew = dold + (2xp + 3); consequentemente ∆E = 2xp + 3.
Se dold ≥ 0, SE ´ escolhido, e o pr´ximo ponto-m´dio ser´ incrementado de 1 na dire¸˜o x e decre-
e o e a ca
mentado de 1 na dire¸˜o y. Portanto:
ca
3 3
dnew = F (xp + 2, yp − ) = (xp + 2)2 + (yp − )2 − R2 (3.14)
2 2
Como dnew = dold + (2xp − 2yp + 5), ∆SE = 2xp − 2yp + 5.
Note que no caso da reta (equa¸˜o linear), ∆E e ∆N E eram constantes. No caso da circunferˆncia
ca e
(equa¸˜o quadr´tica), E e SE variam a cada passo, sendo fun¸˜es do valor espec´
ca a co ıfico de (xp , yp ), o pixel
escolhido na itera¸˜o anterior (P ´ chamado “ponto de avalia¸˜o”). As fun¸˜es podem ser avaliadas
ca e ca co
diretamente, a cada passo, dados os valores de x e y do pixel escolhido na itera¸˜o anterior. Essa
ca
avalia¸˜o n˜o ´ computacionalmente cara, uma vez que as fun¸˜es s˜o lineares.
ca a e co a
31

33. Figura 3.10: Malha de pixels para o Algoritmo do Ponto-M´dio para circunferˆncias, ilustrando a escolha
e e
entre os pixels E e SE.
Resumindo, os mesmos dois passos executados para o algoritmo do tra¸ado de linhas s˜o executados
c a
para o algoritmo de circunferˆncias:
e
1. escolher o pixel com base no sinal da vari´vel d, calculada na itera¸˜o anterior;
a ca
2. atualizar a vari´vel d com o valor correspondente ao pixel escolhido. A diferen¸a ´ que, na atua-
a c e
liza¸˜o de d, calculamos uma fun¸˜o linear do ponto de avalia¸˜o.
ca ca ca
Falta ainda calcular a condi¸˜o inicial (o 1o valor de d). Limitando a utiliza¸˜o do algoritmo a raios
ca ca
inteiros no segundo octante, o pixel inicial ´ dado por (0, R). O pr´ximo “ponto-m´dio” est´ em (1, R− 1 ),
e o e a 2
1
e portanto F (1, R − 2 ) = 1 + (R2 − R + 1 ) − R2 = 5 − R. O algoritmo, bastante parecido com o algoritmo
4 4
para tra¸ado de retas, ´ mostrado no Algoritmo 3.4.
c e
Figura 3.11: Segundo octante da circunferˆncia gerado com o algor´
e ıtimo do Ponto-M´dio e primeiro
e
octante gerado por simetria.
32

34. void MidPointCircle(int r, int color){
int x, int y;
float d;
/* Valores iniciais */
x = 0;
y = r;
d = 5/4 - r;
CirclePoints(x, y, color);
while (y > x){
if (d < 0){
/* Selecione E */
d = d + 2 * x + 3;
x++;
}else{
/* Selecione SE */
d = d + 2 * (x - y) + 5;
x++;
y--;
}/*end if*/
CirclePoints(x, y, color);
}/* end while */
}/* end MidpointCircle */
Algoritmo 3.4: Algoritmo do Ponto-M´dio para circunferˆncias (Aritm´tica Real).
e e e
O algoritmo pode ser facilmente modificado para manipular circunferˆncias centradas fora da origem,
e
ou de raios n˜o inteiros. Entretanto, um problema com esta vers˜o ´ a necessidade de usar aritm´tica
a a e e
real, devido ao valor inicial de d.
1
Para eliminar as fra¸˜es, vamos definir uma nova vari´vel de decis˜o, h, onde h = d − 4 , e substituir
co a a
d por h + 4 no c´digo. Agora, a inicializa¸˜o ´ h = 1 − R, e a compara¸˜o d < 0 torna-se h < − 1 .
1
o ca e ca 4
Entretanto, como o valor inicial de h ´ inteiro, e a vari´vel ´ incrementada de valores inteiros (∆E e
e a e
∆SE), a compara¸˜o pode ser alterada simplesmente para h < 0. Temos agora um algoritmo que opera
ca
em termos de h, usando apenas aritm´tica inteira, que ´ mostrado no Algoritmo 3.5. (Para manter a
e e
nota¸˜o consistente com o algoritmo de linhas, substituimos novamente h por d). A Figura 3.11 mostra
ca
o segundo octante de uma circunferˆncia de raio 14 gerada pelo algoritmo.
e
Diferen¸as de Segunda Ordem
c
´
E poss´ ıvel melhorar o desempenho do algoritmo usando ainda mais extensivamente a t´cnica da com-
e
puta¸˜o incremental. Vimos que as fun¸˜es s˜o equa¸˜es lineares, e no algoritmo, elas est˜o sendo
ca co a co a
computadas diretamente. Entretanto, qualquer polinˆmio pode ser calculado incrementalmente - assim
o
como foi feito com as vari´veis de decis˜o. (Na verdade, estamos calculando diferen¸as parciais de 1a e
a a c
2a ordens). A estrat´gia consiste em avaliar as fun¸˜es diretamente em dois pontos adjacentes, calcular a
e co
diferen¸a (que no caso de polinˆmios ´ sempre um polinˆmio de menor grau), e aplicar esta diferen¸a a
c o e o c
cada itera¸˜o.
ca
Se escolhemos E na itera¸˜o atual, o ponto de avalia¸˜o move de (xp , yp ) para (xp + 1, yp ). Como
ca ca
vimos, a diferen¸a de 1a ordem ´ ∆Eold em (xp , yp ) = 2xp + 3. Conseq¨entemente,
c e u
∆Enew em (xp + 1, yp ) = 2(xp + 1) + 3 (3.15)
e a diferen¸a de 2a ordem ´ ∆Enew − ∆Eold = 2.
c e
Analogamente, SEold em (xp , yp ) = 2xp − 2yp + 5. Conseq¨entemente,
u
∆SEnew em(xp + 1, yp ) = 2(xp + 1) − 2yp + 5 (3.16)
a
e a diferen¸a de 2 ordem ´ ∆SEnew − ∆SEold = 2.
c e
Se escolhemos SE na itera¸˜o atual, o ponto de avalia¸˜o move de (xp , yp ) para (xp + 1, yp − 1).
ca ca
Conseq¨entemente
u
33

35. void MidPointCircleInt(int r, int color){
int x, int y, d;
/* Valores iniciais */
x = 0;
y = r;
d = 1 - r;
CirclePoints(x, y, color);
while (y > x){
if (d < 0){
/* Selecione E */
d = d + 2 * x + 3;
x++;
}else{
/* Selecione SE */
d = d + 2 * (x - y) + 5;
x++;
y--;
}/*end if*/
CirclePoints(x, y, color);
}/* end while */
}/* end MidpointCircleInt */
Algoritmo 3.5: Algoritmo do Ponto-M´dio para circunferˆncias utilizando aritm´tica inteira.
e e e
∆Enew em(xp + 1, yp − 1) = 2(xp + 1) + 3 (3.17)
e a diferen¸a de 2a ordem ´ ∆Enew − ∆Eold = 2. Al´m disso,
c e e
∆SEnew em(xp + 1, yp − 1) = 2(xp + 1) − 2(yp − 1) + 5 (3.18)
a
e a diferen¸a de 2 ordem ´ ∆SEnew − ∆SEold = 4.
c e
Considerando que ∆E e ∆SE s˜o computados usando o pixel inicial (0, R), a vers˜o final do algoritmo
a a
dada a seguir e consiste dos seguintes passos:
1. escolher o pixel com base no sinal da vari´vel d calculada na itera¸˜o anterior;
a ca
2. atualizar a vari´vel d usando E ou SE, usando o valor de calculado na itera¸˜o anterior;
a ca
3. atualizar os ∆ s para considerar o movimento para o pr´ximo pixel, utilizando as diferen¸as cons-
o c
tantes previamente calculadas; e
4. mover para o pr´ximo pixel. ∆E e ∆SE s˜o computados usando o pixel inicial (0, R).
o a
O algoritmo, bastante utilizando a otimiza¸˜o das diferen¸as de 2a ordem ´ apresentado em no Algo-
ca c e
ritmo 3.6.
3.4 Convers˜o Matricial de Elipses
a
Consideremos a elipse padr˜o da Figura 3.12, centrada em (0, 0). Ele ´ descrita pela equa¸˜o:
a e ca
F (x, y) = b2 x2 + a2 y 2 − a2 b2 = 0 (3.19)
onde 2a ´ o comprimento do eixo maior (eixo x) e 2b ´ o comprimento do eixo menor (eixo y).
e e
Como foi feito para circunferˆncias, tomar-se-´ como base elipses centradas na origem (transla¸˜o !).
e a ca
As elipses possuem simetria horizontal e vertical, assim a preocupa¸˜o ser´ de tra¸ar apenas o primeiro
ca a c
quadrante da elipse e depois tra¸ar os demais por reflex˜o.
c a
Primeiramente dividiremos o primeiro quadrante em duas regi˜es: o limite entre as duas regi˜es ´ o
o o e
ponto da curva cuja tangente tem inclina¸˜o igual a -1. A determina¸˜o deste ponto n˜o ´ t˜o simples.
ca ca a e a
34

36. void MidPointCircleInt(int r, int color){
// Fun¸~o de utiliza diferen¸as parciais de 2a ordem para incrementar variavel de
ca c
// decis~o d. Circunfer^ncia centrada na origem
a e
/* Valores iniciais */
int x = 0;
int y = r;
int d = 1 - r;
int deltaE=3
inte deltaSE= -2*r+5
CirclePoints(x, y, color);
while (y > x){
if (d < 0){ /* Selecione E */
d +=deltaE;
deltaE += 2;
deltaSE += 2;
}else{ /* Selecione SE */
d +=deltaSE;
deltaE += 2;
deltaSE += 4;
y--;
}/*end if*/
x++;
CirclePoints(x, y, color);
}/* end while */
}/* end MidpointCircleInt */
Algoritmo 3.6: Algoritmo MidPoint para convers˜o matricial de circunferˆncias utilizando dife-
a e
ren¸as de 2 a ordem
c
35

37. Figura 3.12: Elipse padr˜o centrada na origem.
a
Para tanto utilizaremos o vetor gradiente que ´ perpendicular ` tangente ` curva no ponto P , definido
e a a
como:
∂F ∂F
GradienteF (x, y) = i+ j = 2b2 xi + 2a2 y j (3.20)
∂x ∂x
Figura 3.13: As duas regi˜e adotadas, definidas pela tangente a 45o .
o
O limite entre as duas regi˜es ´ o ponto cuja inclina¸˜o da curva ´ -1, e este ponto ocorre quando
o e ca e
o vetor gradiente tem inclina¸˜o igual a 1, isto ´, quando os componentes nas dire¸˜es i e j s˜o de
ca e co a
magnitudes iguais. A componente j do gradiente ´ maior do que a i na regi˜o 1, e vice-versa na regi˜o
e a a
2. Assim, se o pr´ximo “ponto-m´dio” ´ a2 (yp − 1 ) ≤ b2 (xp + 1), n´s mudamos da regi˜o 1 para a regi˜o
o e e 2 o a a
2 (ver Figura 3.13).
Como nos outros algoritmos de “ponto-m´dio” anteriores, o sinal da vari´vel de decis˜o d (´ o valor
e a a e
da fun¸˜o no “ponto-m´dio”) ser´ usado para verificar que pixels fazem ou n˜o parte da elipse.
ca e a a
Assim, na regi˜o 1, se o pixel corrente est´ em (xp , yp ), ent˜o a vari´vel de decis˜o para a regi˜o
a a a a a a
1, d1, ´ F (xp + 1, yp − 1 ), o ponto m´dio entre E e SE. Repetindo o processo de deriva¸˜o para a
e 2 e ca
fun¸˜o de incremento (como foi feito para circunferˆncia), tem-se que ∆E = b2 (2xp + 3) e ∆SE =
ca e
b2 (2xp + 3) + a2 (−2yp − 1).
36

38. Para a regi˜o 2, se o pixel corrente est´ em (xp , yp ), ent˜o a vari´vel de decis˜o para a regi˜o 2, d2,
a a a a a a
1
´ F (xp + 2 , yp − 1), o ponto m´dio entre S e SE. Pode-se fazer c´lculos idˆnticos aos da regi˜o 1.
e e a e a
A condi¸˜o inicial deve ser ent˜o computada. Assumindo valores inteiros para a e b, a elipse come¸a
ca a c
em (0, b), e o primeiro “ponto-m´dio” ´ calculado em (1, b − 1 ). Assim,
e e 2
1 1 1
F (1, b − ) = b2 + a2 (b − )2 − a2 b2 = b2 + a2 (−b + ) (3.21)
2 2 4
void MidpointElipse(int a, int b, int color){
int x, int y;
float d1, d2;
/* Valores iniciais */
x = 0;
y = b;
d1 = b * b - a * a * b + a * a / 4.0;
ElipsePoints(x, y, color); /* Simetria de ordem 4 */
while(a * a * (y - 0.5) > b * b * (x + 1)){
/* Regi~o 1 */
a
if (d1 < 0)
d1 = d1 + b * b * (2 * x + 3);
x++
}else{
d1 = d1 + b * b * (2 * x + 3) + a * a * (-2 * y + 2);
x++;
y--;
}/*end if*/
ElipsePoints(x, y, color);
}/* end while */
d2 = b * b * (x + 0.5) * (x + 0.5) + a * a * (y - 1) * (y - 1) - a * a * b * b;
while(y > 0){
/* Regi~o 2 */
a
if (d2 < 0){
d2 = d2 + b * b * (2 * x + 2) + a * a * (-2 * y + 3);
x++;
y--;
}else{
d2 = d2 + a * a * (-2 * y + 3);
y--;
}/*end if*/
ElipsePoints(x, y, color);
}/* end while */
}/*end MidpointElipse*/
Algoritmo 3.7: Algoritmo do Ponto-M´dio para convers˜o matricial de elipses.
e a
3.5 Corre¸˜o no Tra¸ado
ca c
Para a maioria dos dispositivos gr´ficos, o retˆngulo de visualiza¸˜o n˜o ´ quadrado, e as densidades de
a a ca a e
pixels na horizontal e na vertical s˜o diferentes. Ou seja, a raz˜o de aspecto f´
a a ısica raramente ´ igual
e
a 1, e a consequˆncia ´ uma distor¸˜o vis´
e e ca ıvel no tra¸ado. Por exemplo, um quadrado (especificado
c
em coordenadas do usu´rio) pode ser deformado num retˆngulo ao ser convertido em coordenadas do
a a
dispositivo, ou uma circunferˆncia pode ser distorcida numa elipse.
e
A forma mais simples de corrigir esta deforma¸˜o ´ atrav´s de uma transforma¸˜o de escala dos dados
ca e e ca
que definem a curva a ser tra¸ada. Ou seja, no caso da circunferˆncia, bastaria converter os pontos
c e
que definem a circunferˆncia em pontos que na verdade definem uma elipse, mas que, como existe a
e
deforma¸˜o, aparecem na tela como uma circunferˆncia.
ca e
37

39. As diferen¸as de densidades representam de fato uma opera¸˜o de escala n˜o homogˆnea realizada
c ca a e
pelo dispositivo. Para corrig´ basta aplicar-se aos parˆmentros das curvas a serem tra¸adas uma
ı-la a c
transforma¸˜o de escala inversa, que compense a do dispositivo. Por exemplo, se a densidade horizontal
ca
´ o dobro da densidade vertical, ent˜o as abcissas dos pontos extremos de cada segmento a tra¸ar devem
e a c
ser dobradas para que mantenham a mesma propor¸˜o em rela¸˜o `s ordenadas. Essa manipula¸˜o dos
ca ca a ca
pontos das curvas deve ser feita pelo programa que efetua a interface entre os programas do usu´rio ea
os dispositivos gr´ficos de sa´ - os chamados Pacotes gr´ficos de interfaceamento, ou Ambientes
a ıda a
Gr´ficos.
a
Outra quest˜o complexa ´ a elimina¸˜o do efeito de “serrilhado” (aliasing) observ´vel nas imagens
a e ca a
geradas por m´todos de convers˜o matricial. Este efeito ´ mais pronunciado nos trechos de arcos com
e a e
inclina¸oes pr´ximas da horizontal ou vertical. As t´cnicas usualmente aplicadas para a corre¸˜o desse
c o e ca
efeito s˜o “caras” (do ponto de vista computacional), e exigem que se fa¸a um controle de intensidade do
a c
tra¸o.
c
As t´cnicas de anti-serrilhado (antialiasing) tra¸am n˜o s´ os pixels calculados pelo procedimento de
e c a o
convers˜o matricial, mas tamb´m os pixels vizinhos, acima e abaixo, com intensidades vari´veis, que ser˜o
a e a a
tanto maiores quanto mais pr´ximos os pixels estiverem do centro da reta. O c´lculo das intensidades
o a
dos pixels e a determina¸˜o das suas coordenadas s˜o processos n˜o triviais, e requerem um n´mero bem
ca a a u
maior de opera¸˜es do que o efetuado pelos algoritmos de convers˜o estudados.
co a
3.6 Antialising
As primitivas geradas apresentam o problema da aparˆncia “serrilhada”, ou “efeito escada”. Este efeito
e
indesej´vel ´ o resultado da abordagem “tudo ou nada” adotada no processo de convers˜o matricial, no
a e a
qual cada pixel recebe a cor associada ` primitiva ou mant´m a sua cor original. Esse efeito ´ apenas
a e e
uma das v´rias manifesta¸˜es vis´
a co ıveis do fenˆmeno conhecido como aliasing. A aplica¸˜o de t´cnicas que
o ca e
reduzem (ou eliminam) o efeito de aliasing ´ denominado antialising, e primitivas ou imagens geradas
e
utilizando tais t´cnicas s˜o ditas antialiased.
e a
Considere o algoritmo do ponto m´dio para tra¸ado de segmentos de reta sendo usado para tra¸ar
e c c
uma linha preta de um pixel de espessura, com inclina¸˜o entre 0 e 1, em um fundo branco. Em cada
ca
coluna de pixels interceptada pela linha o algoritmo seta a cor preta ao pixel que est´ mais perto do ponto
a
ideal pertencente ` linha. A cada vez que se passa para a pr´xima coluna e o pixel mais pr´ximo da linha
a o o
ideal ´ o que est´ a nordeste (NE), e n˜o ` leste (E), ocorre um “efeito escada”. O mesmo acontece em
e a a a
outros tipos de primitivas. Uma forma de reduzir o problema (em termos visuais) ´ aumentar a resolu¸˜o
e ca
do dispositivo (usar mais pixels) (ver Figura 3.14) . Esta ´ uma solu¸˜o cara em termos de mem´ria
e ca o
e tempo gasto no processo de convers˜o matricial, e que n˜o resolve o problema. Alternativas menos
a a
custosas s˜o descritas a seguir.
a
Figura 3.14: Segmento de reta renderizado com o algor´
ıtmo do ponto m´dio em diferentes escalas. (a) ´
e e
uma aplia¸˜o da regi˜o central de (b).
ca a
3.6.1 ´
Amostragem de Areas n˜o Ponderada
a
O fato ´ que, apesar da primitiva ideal, como um segmento de reta, ter espessura zero, a primitiva
e
sendo tra¸ada tem espessura n˜o nula, pois ocupa uma ´rea finita da tela. Assim, podemos pensar em
c a a
um segmento de reta como um retˆngulo com uma certa espessura que cobre uma regi˜o da malha de
a a
38

40. pixels, como ilustrado na Figura 3.15. Conseq¨entemente, o melhor procedimento n˜o ´ atribuir o valor
u a e
correspondente a preto a um unico pixel em uma coluna, mas atribuir diferentes intensidades da cor a cada
´
pixel interceptado pela ´rea coberta pelo retˆngulo que aproxima a linha, na coluna em quest˜o. Assim,
a a a
linhas horizontais ou verticais, cuja espessura ´ 1 pixel, afetam exatamente 1 pixel em uma coluna ou
e
linha. Para linhas com outras inclina¸˜es, mais do que 1 pixel ´ tra¸ado, cada qual com uma intensidade
co e c
apropriada.
Figura 3.15: Segmento de reta definido com uma espessura diferente de zero.
Mas, qual ´ a geometria de um pixel? Qual o seu tamanho? Qual intensidade a atribuir a um
e
´
pixel interceptado pela linha? E computacionalmente simples assumir que os pixels definem uma malha
regular de “quadrados” n˜o sobrepostos que recobre a tela, sendo que as intersec¸˜es da malha definem
a co
o posicionamento dos pixels, i.e., pixels s˜o tratados como “quadrados” com centro nas interse¸˜es da
a co
malha. Uma primitiva pode sobrepor toda ou parte da ´rea ocupada por um pixel. Assumimos tamb´m
a e
que a linha contribui para a intensidade do pixel segundo um valor proporcional ` porcentagem da ´rea do
a a
pixel coberta por ela. Se a primitiva cobre toda a ´rea do pixel, ele recebe a intensidade m´xima (preto,
a a
no caso), se cobre parte o pixel recebe um tom de cinza cuja intensidade ´ proporcional ` ´rea coberta
e aa
(Figura 3.16). O efeito ´ “suavizar” a defini¸˜o da reta ou das arestas que definem a primitiva, melhorando
e ca
sua aparˆncia visual quando observada ` distˆncia. Essa estrat´gia ´ denominada amostragem por ´rea
e a a e e a
n˜o ponderada (unweighted area sampling). Uma estrat´gia ainda mais eficiente ´ a amostragem por ´rea
a e e a
ponderada (weighted area sampling).
Figura 3.16: A intensidade do pixel ´ proporcional ` area coberta.
e a
´
Amostragem de Areas Ponderada
Nessa outra estrat´gia, assim como na anterior, valem duas propriedades: 1) a intensidade atribu´ ao
e ıda
pixel ´ diretamente proporcional ` ´rea do mesmo coberta pela primitiva; 2) se a primitiva n˜o intercepta
e aa a
a ´rea do pixel, ent˜o ela n˜o contribui nada para a cor do mesmo. A diferen¸a ´ que, na estrat´gia
a a a c e e
ponderada, ao determinar a contribui¸˜o de uma ´rea considera-se, tamb´m, a sua proximidade em rela¸˜o
ca a e ca
ao centro do pixel. Assim, ´reas iguais podem contribuir de forma desigual: uma ´rea pequena pr´xima
a a o
do centro do pixel tem maior influˆncia do que uma ´rea grande a uma distˆncia maior. Entretanto,
e a a
para garantir que a primitiva contribui para um pixel apenas se ela sobrep˜e a ´rea ocupada pelo mesmo,
o a
precisamos mudar a geometria do pixel da seguinte forma: vamos considerar que o pixel ocupa uma ´rea a
39

41. circular maior do que a ´rea quadrangular considerada na situa¸˜o anterior. Se a primitiva sobrep˜e essa
a ca o
nova ´rea, ela contribui para a intensidade do pixel.
a
Vamos definir uma fun¸˜o peso que determina a influˆncia, na intensidade do pixel, de uma ´rea
ca e a
pequena da primitiva, denominada dA, em fun¸˜o da distˆncia de dA ao centro do pixel. No caso da
ca a
amostragem n˜o ponderada, essa fun¸˜o ´ constante, e no caso da amostragem ponderada, ela diminui
a ca e
de forma inversamente proporcional ` distˆncia em rela¸˜o ao centro do pixel. Podemos pensar nessa
a a ca
fun¸˜o como uma fun¸˜o W (x, y), no plano, cuja altura em rela¸˜o ao plano xy d´ o peso associado `
ca ca ca a a
a
´rea dA no ponto (x, y). Para a amostragem por ´rea n˜o ponderada, essa fun¸˜o ´ representada por
a a ca e
uma ’caixa’, como indicado na Figura 3.17. A figura mostra os pixels como quadrados cujos centros
(marcados) est˜o nas intersec¸˜es da malha regular. A contribui¸˜o de cada pequena ´rea ´ proporcional
a co ca a e
aa
` ´rea multiplicada pelo peso. Portanto, a intensidade total ´ dada pela integral da fun¸˜o peso sobre a
e ca
a
´rea de sobreposi¸˜o. O volume representado por essa integral, W s, ´ sempre uma fra¸˜o entre 0 e 1, e a
ca e ca
intensidade I do pixel ´ dada por Imax.W s. No caso da amostragem n˜o ponderada a altura da ’caixa’
e a
´ normalizada para 1, de forma que o volume da caixa ´ 1. No caso da ´rea da linha cobrir todo o pixel,
e e a
tem-se I = Imax.1 = Imax.
Figura 3.17: Filtro definido por um cubo para um pixel definido por um quadrado.
Vamos agora construir uma fun¸˜o peso para a amostragem ponderada: a fun¸˜o adotada tem valor
ca ca
m´ximo no centro do pixel e diminui linearmente a medida que a distˆncia ao centro aumenta, e seu
a a
gr´fico define um cone, como indicado na Figura 3.18. A base do cone ´ uma circunferˆncia cujo centro
a e e
coincide com o centro do pixel, e cujo raio corresponde a uma unidade da distˆncia entre os pixels na
a
malha. Note que as bases das fun¸˜es peso em diferentes pixels se sobrep˜em, e portanto uma unica
co o ´
pequena regi˜o da primitiva pode contribuir para a intensidade de diferentes pixels. Essa sobreposi¸˜o
a ca
tamb´m garante que n˜o existem ´reas da grade que n˜o s˜o cobertas por algum pixel (esse n˜o seria o
e a a a a a
caso se o raio da base fosse de meia unidade, por exemplo).
Figura 3.18: Filtro cˆnico com diˆmetro igual ao dobro da largura de um pixel.
o a
Assim como na fun¸˜o ’caixa’, a soma das contribui¸˜es de intensidade para o cone ´ dada pelo
ca co e
40

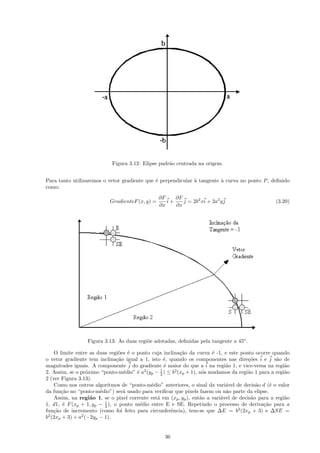
42. volume sob o cone que est´ na regi˜o de interse¸˜o da primitiva com a base do cone. Esse volume, W s,
a a ca
´ uma se¸˜o vertical do cone, como mostrado na Figura 3.18. A altura do cone ´ normalizada para que
e ca e
o volume do mesmo seja igual a 1, garantindo que um pixel que est´ inteiramente sob a base do cone
a
seja tra¸ado com intensidade m´xima. Contribui¸˜es de ´reas da primitiva que interceptam a base mas
c a co a
est˜o distantes do centro do pixel s˜o pequenas, mas ´reas muito pequenas, por´m pr´ximas do centro
a a a e o
do pixel contribuem mais para a cor do mesmo. O resultado dessa abordagem ´ reduzir o contraste entre
e
pixels adjacentes, de forma a gerar transi¸˜es visuais mais suaves. Particularmente, linhas horizontais
co
ou verticais com espessura de um pixel agora resultam em mais do que uma unica linha ou coluna de
´
pixels acesos, o que n˜o ocorre na abordagem n˜o ponderada. Essa abordagem pode ser embutida nos
a a
algoritmos de convers˜o matricial, como descrito em Foley et al. [Fol90, se¸˜o 3.17.4]. Outros tipos de
a ca
fun¸˜es podem ser usadas, sendo que existem fun¸˜es ´timas melhores do que a fun¸˜o cˆnica (v. Foley,
co co o ca o
se¸˜o 4.10).
ca
41

43. Cap´
ıtulo 4
Preenchimento de Pol´
ıgonos
A tarefa de preencher um pol´
ıgono pode ser dividida em duas:
1. Decidir que pixels pintar para preencher o pol´
ıgono;
2. Decidir com que valor pintar o pixel.
Geralmente decidir que pixels devem ser pintados, consiste em se varrer (scan) sucessivas linhas
que interceptam a primitiva, preenchendo os pixels em “blocos” (span) que est˜o dentro da primitiva
a
(que define o pol´ ıgono) da esquerda para a direita. Vamos considerar inicialmente o preenchimento de
primitivas gr´ficas n˜o “recortadas” (unclipped ) com uma unica cor. Em geral, a decis˜o sobre quais pixels
a a ´ a
preencher ´ feita “varrendo-se” (scan) linhas sucessivas que interceptam a primitiva, e preenchendo, da
e
esquerda para a direita, blocos de pixels adjacentes (spans) que est˜o dentro da primitiva que define o
a
pol´
ıgono.
4.1 Retˆngulos
a
Para preencher um retˆngulo com uma unica cor, pinta-se cada pixel dentro de uma linha de varredura
a ´
da esquerda para a direita com o mesmo valor de pixel, isto ´, pode-se preencher cada “bloco” de xmin
e
a xmax. As primitivas para blocos exploram a Coerˆncia Espacial: o fato que freq¨entemente n˜o h´
e u a a
altera¸˜o nas primitivas de um pixel para outro (pixels adjacentes) dentro de um bloco (span) ou de uma
ca
linha de varredura para a pr´xima linha de varredura. Assim, podemos explorar a coerˆncia para buscar
o e
apenas os pixels em que ocorrem mudan¸as. Para um retˆngulo preenchido com a mesma cor, todos
c a
os pixels num bloco receber˜o um mesmo valor, o que garante coerˆncia de bloco (span coherence). O
a e
retˆngulo tamb´m exibe coerˆncia de linha de varredura (scan-line coherence), no sentido de que linhas
a e e
de varredura consecutivas que interceptam o retˆngulo s˜o idˆnticas. Posteriormente consideraremos
a a e
tamb´m coerˆncia de arestas (edge coherence) para lados de pol´
e e ıgonos em geral. Coerˆncia ´ uma pro-
e e
priedade bastante explorada em CG, n˜o apenas para convers˜o matricial de primitivas 2D, mas tamb´m
a a e
para visualiza¸˜o de primitivas 3D.
ca
A capacidade de tratar v´rios pixels identicamente em um bloco (span) tem especial importˆncia
a a
para a diminui¸˜o de tempo gasto para gravar os pixels no Frame Buffer (mem´ria onde ´ armazenada
ca o e
a imagem). Assim, se em menos acessos a mem´ria pudermos escrever mais pixels estaremos ganhando
o
tempo. Abaixo colocaremos um algoritmo para preencher um retˆngulo, sendo que nele n´s n˜o nos
a o a
preocuparemos em escrever eficientemente na mem´ria. Deixaremos isso para discuss˜o posterior.
o a
Para y = ymin at´ ymax do ret^ngulo { Por linha de varredura }
e a
Para x = xmin at´ xmax { Cada pixel dentro do bloco }
e
write_pixel (x,y,valor)
Algoritmo 4.1: Trecho de Algoritmo para Preenchimento de Retˆngulo.
a
Consideremos agora dois retˆngulos que compartilham um mesmo lado. Se preenchermos cada
a
retˆngulo isoladamente, o lado (aresta) compartilhado pelos dois ser´ gerado duas vezes o que n˜o ´
a a a e
desej´vel (perco tempo!). Aqui surge o problema de defini¸˜o de ´rea pertencente a cada primitiva,
a ca a
isto ´, quais os pixels que pertencem a cada primitiva e quais os pixels que n˜o pertencem. De forma
e a
natural, podemos definir os pixels que matematicamente se encontram no interior de uma ´rea definida
a
pela primitiva, como pertencente a ela. Mas o que podemos falar acerca dos pixels que est˜o no limite
a
da primitiva?
42

44. Se voltamos ao nosso problema do retˆngulo podemos adotar como uma regra que: os pixels que
a
constituem os limites da primitiva, isto ´, os que est˜o sobre os seus lados, n˜o s˜o considerados parte
e a a a
da primitiva se o meio-plano definido pelo lado e que cont´m a primitiva est´ abaixo ou a esquerda do
e a
lado. Ou, mais claramente, os pixels que est˜o sobre os lados (aresta) esquerdo e inferior pertencem a
a
primitiva e ser˜o desenhados, por´m os lados superior e direito n˜o pertencem a primitiva e portanto n˜o
a e a a
ser˜o desenhados. Assim, uma aresta vertical compartilhada por dois retˆngulos pertence ao lado que
a a
est´ mais a direita. Sendo que na realidade, blocos dentro de um retˆngulo representam uma intervalo
a a
que ´ fechado a esquerda e embaixo e aberto em cima e a direita.
e
Algumas considera¸˜es devem ser feitas sobre esta regra:
co
1. A regra se aplica da mesma forma a pol´
ıgonos arbitr´rios e n˜o somente a retˆngulos.
a a a
2. O v´rtice do canto inferior esquerdo ainda continua sendo desenhado duas vezes.
e
3. A regra pode tamb´m ser aplicada para retˆngulos e pol´
e a ıgonos n˜o preenchidos.
a
4. A regra faz com que em cada bloco esteja faltando o seu pixel mais a direita, e em cada retˆngulo
a
fique faltando o seu lado (aresta) superior.
Os problemas apresentados nas considera¸˜es acima demonstram que n˜o h´ solu¸˜o perfeita para o
co a a ca
problema de n˜o escrever mais de uma vez linhas que sejam potencialmente compartilhadas por mais de
a
um pol´
ıgono.
4.2 Pol´
ıgonos de Forma Arbitr´ria
a
O algoritmo que vamos discutir a seguir contempla tanto pol´ ıgonos cˆncavos quanto pol´
o ıgonos convexos,
mesmo que eles tenham auto-intersec¸˜o e buracos em seu interior. Ele opera computando blocos de
ca
pixels que est˜o entre os lados esquerdo e direito do pol´
a ıgono. O extremo do bloco ´ calculado por um
e
algoritmo incremental que calcula a linha de varredura/lado de intersec¸˜o a partir da intersec¸˜o com a
ca ca
linha de varredura anterior.
Figura 4.1: Esta figura ilustra o processo de linha de varredura para um pol´
ıgono arbitr´rio. As in-
a
tersec¸˜es da linha de varredura 8 com os lados FA e CD possuem coordenadas inteiras, enquanto as
co
intersec¸˜es com os lados EF e DE possuem coordenadas reais.
co
´
E preciso determinar que pixels da linha de varredura est˜o dentro do pol´
a ıgono, e estabelecer os pixels
correspondentes (no exemplo da Figura 4.1, blocos para x = 2 at´ 4 e 9 at´ 13) com seu valor apropriado.
e e
Repetindo este processo para cada linha de varredura que intercepta o pol´ ıgono, o pol´ıgono inteiro ´e
convertido. A Figura 4.2 ilustra este processo.
Devemos nos preocupar com a defini¸˜o dos pontos extremos do pol´
ca ıgono. Uma forma de obtˆ-los ´
e e
usar o algoritmo de convers˜o de linhas do “Ponto-M´dio” para cada lado do pol´
a e ıgono. Note que esta
estrat´gia inclui alguns pixels no extremo do pol´
e ıgono que na realidade n˜o se encontram no pol´
a ıgono.
Eles foram escolhidos pelo algoritmo de convers˜o matricial de linhas, e s˜o colocados sobre o lado porque
a a
est˜o mais pr´ximas a ele.
a o
N˜o podemos desenhar pixels que n˜o perten¸am verdadeiramente ao interior do pol´
a a c ıgono, pois po-
demos estar invadindo o dom´ ınio de outro pol´
ıgono. Isto ´, se a linha em quest˜o define um extremo
e a
43

45. Figura 4.2: Linhas de varredura em um pol´
ıgno. Os extremos em preto, e os pixels no interior em cinza.
(a) Extremo calculado pelo algoritmo do ”Meio-Ponto”. (b) Extremo interior ao pol´ıgno.
que ´ compartilhado por outro pol´
e ıgono, estaremos entrando na regi˜o definida por ele. Assim, ´ ´bvio
a eo
que ´ prefer´ tra¸ar apenas os pixels que estejam estritamente na regi˜o definida pelo pol´
e ıvel c a ıgono, mesmo
que um pixel exterior esteja mais pr´ximo a aresta real (pelo algoritmo de convers˜o (“Ponto-M´dio”)).
o a e
Logo, o algoritmo de convers˜o deve ser ajustado de acordo. Compare a Figura 4.2(a) com 2(b), e note
a
que os pixels fora da primitiva n˜o s˜o desenhados na parte (b).
a a
Com esta t´cnica, um pol´
e ıgono n˜o invade a regi˜o definida por outro - a mesma t´cnica pode ser
a a e
aplicada para pol´ıgonos n˜o preenchidos, por uma quest˜o de consistˆncia. Poder´
a a e ıamos, alternativamente,
converter retˆngulos e pol´
a ıgonos n˜o cheios convertendo independentemente cada segmento de reta que
a
os comp˜e, mas nesse caso pol´
o ıgonos cheios e n˜o cheios n˜o teriam os mesmos pixels na fronteira!
a a
Como no algoritmo original do “Ponto-M´dio”, podemos usar um algoritmo incremental para calcular
e
o bloco (span) extremo sobre uma linha de varredura a partir da linha de varredura anterior, sem ter que
calcular analiticamente os pontos de intersec¸˜o da linha de varredura com os lados do pol´
ca ıgono.
O processo de preencher os pol´ ıgonos pode ser dividido em trˆs passos:
e
1. Obter a intersec¸˜o da linha de varredura com todos os lados do pol´
ca ıgono.
2. Ordenar os pontos de intersec¸˜o (em x crescente).
ca
3. Preencher os pixels entre pares de pontos de intersec¸˜o do pol´
ca ıgono que s˜o internos a ele. Para
a
determinar quais os pares que s˜o internos ao pol´
a ıgono, podemos usar a regra de Paridade: A
paridade inicialmente ´ par, e a cada intersec¸˜o encontrada o bit de paridade ´ invertido, o pixel
e ca e
´ pintado quando a paridade ´ impar, e n˜o ´ pintado quando ´ par.
e e a e e
Vamos tratar dos dois primeiros passos do processo mais adiante, e consideremos agora a estrat´gia
e
usada para o preenchimento dos blocos (passo 3). Na Figura 4.1, a lista ordenada de coordenadas x ´ (2,
e
4.5, 8.5, 13) para a linha de varredura 8. H´ 4 pontos a serem discutidos sobre este passo:
a
I Se a intersec¸˜o ´ um valor fracion´rio, como determinar qual o pixel que dever´ ser
ca e a a
tomado para que fique interior ao pol´ ıgono?
O valor dever´ ser arredondado de forma a que o ponto fique dentro do pol´
a ıgono. Se estamos dentro
do pol´ıgono (paridade ´
ımpar) e atingimos uma intersec¸˜o fracion´ria pela direita, arredondamos
ca a
a coordenada x da intersec¸˜o para baixo; se estamos fora do pol´
ca ıgono arrendondamos para cima.
Isso garante que sempre teremos um ponto dentro do pol´ ıgono.
II Como tratar o caso de intersec¸˜o com coordenadas inteiras?
ca
Pode-se utilizar o crit´rio visto anteriormente, para evitar conflitos entre lados compartilhados em
e
retˆngulos. Se a coordenada x de um pixel mais a esquerda de um bloco (span) ´ inteira ele
a e
´ definido como interno; se a coordenada x do pixel mais a direita de um bloco ´ inteira, ele ´
e e e
definido como externo ao pol´ ıgono.
III Como tratar o caso II para v´rtices que s˜o compartilhados por mais de uma aresta
e a
do pol´
ıgono?
Usamos a t´cnica de paridade. Ou seja, contamos o v´rtice de ymin de um lado para alterar a
e e
paridade, mas n˜o contamos o v´rtice de ymax, dessa forma o v´rtice de ymax ´ desenhado somente
a e e e
44

46. se ele ´ o v´rtice de ymin do lado adjacente. Por exemplo, na Figura 4.1, o v´rtice A ´ contado uma
e e e e
vez no c´lculo de paridade porque ´ o v´rtice de ymin para o lado FA, mas ´ tamb´m o v´rtice de
a e e e e e
ymax para o lado AB. Assim ambos os lados e blocos s˜o tratados como intervalos que s˜o fechados
a a
em seu valor m´ ınimo e abertos em seu valor m´ximo.
a
IV Como tratar o caso especial de II em que os v´rtices definem uma linha horizontal?
e
Assim como no caso dos retˆngulos, arestas horizontais inferiores s˜o tra¸adas, e arestas horizontais
a a c
superiores n˜o s˜o. Como veremos, isso acontece automaticamente se n˜o contarmos os v´rtices
a a a e
dessas arestas no c´lculo da paridade, o que ´ natural, j´ que eles n˜o correspondem a v´rtices ymin
a e a a e
ou ymax.
Ilustremos este processo, aplicando essas regras ` linha de varredura 8, na Figura 4.1. Os pixels
a
ser˜o preenchidos a partir do ponto a (coordenadas (2, 8)), at´ o primeiro pixel a esquerda do ponto b
a e
(coordenadas (4, 8)); e do primeiro pixel a direita do ponto c (coordenadas (9, 8)) at´ 1 pixel a esquerda
e
do ponto d (coordenadas (12, 8)). Para a linha de varredura 3, o v´rtice A conta uma vez porque ´ o
e e
v´rtice de ymin do lado FA (e ´ tamb´m o v´rtice ymax do lado AB), isto causa paridade ´
e e e e ımpar, assim o
bloco ´ desenhado a partir de A at´ um pixel a esquerda da intersec¸˜o com o lado CB, onde a paridade
e e ca
´ estabelecida como par e o bloco ´ terminado. A linha de varredura 1 passa apenas pelo v´rtice B, e
e e e
os lados AB e BC tem como v´rtice de ymin B, o qual ´ dessa forma contado como paridade par. Este
e e
v´rtice atua como um bloco nulo, pois a linha de varredura entra pelo v´rtice, desenha o pixel e sai por
e e
ele mesmo. Assim, um pixel m´ ınimo local ´ pintado, por´m pixel de m´ximo local n˜o o ´. Isso acontece
e e a a e
com a intersec¸˜o da linha de varredura 9 com o v´rtice F, compartilhado pelos lados FA e EF. Para
ca e
ambos os lados, B ´ v´rtice ymax, e dessa forma n˜o afeta a paridade, que continua par.
e e a
Figura 4.3: Tratamento dos lados horizontais de um pol´
ıgono.
4.2.1 Arestas Horizontais
Examinemos os casos apresentados na Figura 4.3. Consideremos o lado AB (lado inferior). O v´rtice A
e
´ v´rtice ymin para o lado JA, e AB por ser horizontal n˜o possui m´
e e a ınimo. Assim, a paridade ´ ´e ımpar
(pela regra da paridade!) e o bloco (span) ´ desenhado. O lado vertical BC tem ymin em B, e pela
e
mesma raz˜o anterior o lado AB n˜o contribui para alterar a paridade, assim a paridade torna-se par e o
a a
bloco termina. O lado IJ tem v´rtice ymin em J (e em JA ele ´ m´ximo) assim a paridade torna-se ´
e e a ımpar
e o bloco ´ desenhado at´ o lado BC. O bloco que come¸a em IJ e encontra C, n˜o termina a´ porque
e e c a ı,
C ´ ymax para BC, assim o bloco continua sobre o lado CD (at´ D), no entanto DE tem ymin em D e
e e
a paridade torna-se par e o bloco termina. O lado IJ tem ymax em I e o lado HI n˜o contribui para a
a
c´lculo da paridade, assim a paridade continua e o bloco sobre o lado HI n˜o ´ desenhado. Entretanto, o
a a e
lado GH tem v´rtice ymin em H, e a paridade torna-se ´
e ımpar, e o bloco ´ desenhado a partir de H at´ o
e e
pixel a direita da intersec¸˜o da linha de varredura com o lado EF. Finalmente n˜o h´ v´rtice ymin em
ca a a e
G nem em F, e dessa forma o lado (que ´ o lado superior - topo) FG n˜o ´ desenhado.
e a e
¸˜
OBSERVACOES:
• O algoritmo acima contempla pol´ ıgonos que possuem auto-intersec¸˜o. Mas n˜o desenha os pixels
ca a
das arestas superiores nem os das arestas ` direita, mesmo se a primitiva for isolada.
a
• N˜o desenha os pixels sobre o topo interno de um pol´
a ıgono cˆncavo em formato de U.
o
45

47. • N˜o desenha os pixels que s˜o pontos m´ximos locais.
a a a
• Neste algoritmo, em vez de escrever pixels em lugares errados, pixels n˜o s˜o escritos (mesmo em
a a
seus lugares certos!).
4.2.2 Slivers
Existe um outro problema com o nosso algoritmo de convers˜o matricial: pol´
a ıgonos com lados muito
pr´ximos criam um “sliver” - uma ´rea poligonal t˜o estreita que seu interior n˜o cont´m um bloco de
o a a a e
pixels para cada linha de varredura (Figura 4.4). Devido ` regra de que s˜o tra¸ados apenas os pixels que
a a c
estejam no interior ou sobre arestas inferiores ou a esquerda, podem existir muitas linhas de varredura
com um unico pixel, ou sem nenhum. A ausˆncia de pixels ´ um outro exemplo do problema de aliasing,
´ e e
ou seja, da representa¸˜o de um sinal cont´
ca ınuo atrav´s de uma aproxima¸˜o discreta (digital). Para
e ca
melhorar a aparˆncia nesses casos, pode-se usar t´cnicas de antialiasing (se tivermos m´ltiplos bits por
e e u
pixel). Antialiasing implicaria em “suavizar” nossa regra de “tra¸ar apenas pixels que estejam no interior
c
ou numa aresta inferior ou ` esquerda”, de forma a permitir que pixels na fronteira ou mesmo no exterior
a
do pol´ıgono assumam intensidades variando como uma fun¸˜o da distˆncia entre o centro do pixel e a
ca a
primitiva. Nesse caso, m´ltiplas primitivas podem contribuir para o valor de um pixel.
u
Figura 4.4: Exemplo de uma convers˜o matricial de um Sliver
a
4.2.3 Algoritmo para Convers˜o Matricial de Segmento de Reta que Utiliza
a
“Coerˆncia de Arestas” de um Pol´
e ıgono
No m´todo anterior us´vamos “for¸a bruta” para calcular a intersec¸˜o da linha de varredura com os
e a c ca
lados de um pol´ıgono. Mas, freq¨entemente, somente poucos lados de um pol´
u ıgono s˜o de interesse para
a
uma dada linha de varredura. Al´m disso, notemos que muitos lados interceptados por uma linha de
e
varredura i tamb´m o s˜o pela linha de varredura i + 1. Esta “Coerˆncia de Arestas” ocorre para muitas
e a e
linhas de varreduras que interceptam um lado. Ao movermos de uma linha de varredura para a pr´xima,
o
podemos calcular o pr´ximo x da intersec¸˜o da linha de varredura com o lado, a partir do x da linha
o ca
de varredura anterior que interceptou o lado. Usando a mesma t´cnica do algoritmo do “Ponto-M´dio”,
e e
temos:
1
xi+1 = xi + (4.1)
m
(ymax−ymin)
onde m = (xmax−xmin) ´ a inclina¸ao da aresta.
e c˜
No algoritmo do ponto-m´dio para convers˜o matricial de segmentos de reta, evitamos usar aritm´tica
e a e
fracion´ria calculando uma vari´vel de decis˜o inteira, e verificando o seu sinal para escolher o pixel mais
a a a
pr´ximo ` reta “verdadeira”. Aqui, tamb´m gostar´
o a e ıamos de usar aritm´tica inteira para calcular o pixel
e
interior mais pr´ximo da verdadeira intersec¸˜o. Consideremos arestas com inclina¸˜o maior que 1 que
o ca ca
s˜o arestas a esquerda. Arestas a direita e outras inclina¸˜es s˜o tratadas com argumentos similares aos
a co a
que ser˜o vistos para esse caso, e arestas verticais s˜o casos especiais. (Arestas horizontais s˜o tratadas
a a a
implicitamente pelas regras de tra¸ado de blocos, como vimos anteriormente.)
c
Precisamos tra¸ar um pixel no extremo (xmin, ymin). A medida que y ´ incrementado, a coordenada
c e
1
x do ponto na linha ideal ser´ aumentada de m . Este aumento resultar´ num valor de x com uma parte
a a
inteira e uma parte fracion´ria, a qual pode ser expressa como uma fra¸˜o com denominador igual a
a ca
46

48. ymax − ymin. Com a repeti¸˜o do processo, a parte fracion´ria vai se tornar maior do que 1 (overflow ),
ca a
e a parte inteira ter´ de ser incrementada. Por exemplo, se a inclina¸˜o ´ 5 , e xmin ´ 3, a seq¨ˆncia de
a ca e 2 e ue
valores de x ser´ a
3, 3 5 , 3 4 , 3 6 = 4 5
2
5 5
1
e assim por diante. Quando a parte fracion´ria de x ´ zero, podemos tra¸ar diretamente o pixel (x, y)
a e c
que est´ sobre a linha, mas quando ela ´ diferente de zero precisamos arredondar (para cima!) de forma a
a e
tomar um pixel que esteja estritamente dentro da linha. Quando a parte fracion´ria de x torna-se maior
a
do que 1, incrementamos x, subtraimos 1 da parte fracion´ria, e movemos um pixel a direita. Se com o
a
incremento obtemos um valor inteiro para x, tra¸amos o pixel correspondente e decrementamos a fra¸˜o
c ca
de 1, de forma a mantˆ-la menor do que 1.
e
Podemos evitar o uso de aritm´tica fracion´ria mantendo apenas o numerador da fra¸˜o, e observando
e a ca
que a parte fracion´ria ser´ maior do que 1 quando o numerador tornar-se maior que o denominador.
a a
O algoritmo abaixo implementa esta t´cnica, usando a vari´vel incremento para armazenar as sucessivas
e a
adi¸˜es feitas no numerador at´ que ocorra um overflow (ultrapasse o denominador), quando o numerador
co e
´ decrementado pelo denominador, e x ´ incrementado.
e e
void LeftEdgeScan (int xmin, int ymin, int xmax, int ymax, int valor){
int x, y;
x = xmin;
y = ymin;
numerador = xmax - xmin;
denominador = ymax - ymin;
incremento = denominador;
for (y = ymin; y <= ymax; y++){
PintaPixel (x,y,valor);
incremento+=numerador;
if (incremento > denominador){
/* Overflow, Arredonda o pr´ximo pixel e decrementa o incremento */
o
x++;
incremento-=denominador;
}/* end if */
}/* end for */
}/* end LeftEdgeScan */
Algoritmo 4.2: Convers˜o matricial da aresta esquerda de um pol´
a ıgono.
Vamos desenvolver um algoritmo de convers˜o matricial de linhas que se aproveita da coerˆncia
a e
de arestas e, para cada linha de varredura, armazena o conjunto de arestas por ela interceptadas numa
estrutura de dados denominada AET - active-edge table (tabela das arestas ativas). As arestas na AET s˜o
a
ordenadas de acordo com as coordenadas x dos pontos de intersec¸˜o, de forma que possamos preencher
ca
os blocos definidos por pares de valores de intersec¸˜o (devidamente arredondados) - que definem as
ca
extremidades dos blocos.
A medida que movemos para a pr´xima linha de varredura, y +1, a AET ´ atualizada. Primeiramente,
o e
arestas que est˜o na AET mas n˜o s˜o interceptadas por esta pr´xima linha de varredura (ou seja, aquelas
a a a o
para as quais ymax = y) s˜o removidas. Depois, quaisquer novas arestas interceptadas por essa linha (ou
a
seja, aquelas para as quais ymin = y + 1) s˜o incluidas na AET. Finalmente, para as arestas que ainda
a
est˜o na AET, os novos valores de x das intersec¸˜es s˜o calculados, usando o algoritmo incremental para
a co a
convers˜o matricial de arestas j´ visto.
a a
Para que a inclus˜o de novas arestas na AET seja eficiente, criamos uma tabela de arestas global
a
(ET - Edge Table), contendo todas as arestas do pol´ ıgono em ordem crescente de sua menor coordenada
y (ymin). A ET ´ uma tabela hashing aberta (v. Aho, Data Structures and Algorithms), com p
e
posi¸˜es (buckets, ou ”cestos”), uma para cada linha de varredura. A cada ”cesto”y ´ associada uma lista
co e
encadeada com as arestas com ymin = y. As arestas na lista est˜o ordenadas em ordem crescente da
a
coordenada x de sua extremidade inferior (xmin). Cada n´ da lista armazena ainda a coordenada ymax
o
1
da aresta, e o incremento em x utilizado para passar para a pr´xima linha de varredura, m . A Figura
o
4.5 mostra como estariam ordenadas as seis arestas do pol´ ıgono da Figura 4.1, e a Figura 4.6 mostra a
47

49. AET para as linhas de varredura 9 e 10 daquele pol´ıgono. Uma vez constru´ a ET, os passos para o
ıda
algoritmo de convers˜o de arestas s˜o dados no Algoritmo 4.3.
a a
Este algoritmo explora coerˆncia de arestas para calcular o valor x das intersec¸˜es e coerˆncia
e co e
de linhas de varredura (juntamente com ordena¸˜o) para calcular blocos. Uma vez que a ordena¸˜o
ca ca
trabalha com um n´mero pequeno de arestas, e a reordena¸˜o do passo 3.6 ´ feita numa lista quase que
u ca e
totalmente ordenada, pode-se usar um m´todo de ordena¸˜o por inser¸˜o, ou o m´todo bubblesort, que ´
e ca ca e e
O(N ).
Figura 4.5: ET para o pol´
ıgono de Figura 4.1.
Para efeito de convers˜o matricial, triˆngulos e trapez´ides podem ser tratados como casos especiais
a a o
de pol´
ıgonos, uma vez que possuem apenas dois lados para cada linha de varredura (lembre-se que lados
horizontais n˜o s˜o convertidos explicitamente). Na verdade, como um pol´
a a ıgono arbitr´rio sempre pode
a
ser decomposto numa malha de triˆngulos que compartilham v´rtices e arestas, poder´
a e ıamos converter
um pol´ ıgono decompondo-o numa malha de triˆngulos, convertendo os triˆngulos a seguir. Este ´ um
a a e
problema cl´ssico da geometria computacional, o da triangula¸˜o. O processo de decomposi¸˜o ´ simples
a ca ca e
para pol´ıgonos convexos.
Figura 4.6: AET para o pol´ıgono da Figura 4.1 a) linha de varredura 9 b) linha de varredura 10. Note
que a coordenada x da aresta DE em (b) foi arredondada para cima..
Note que o c´lculo dos blocos ´ cumulativo. Ou seja, quando a itera¸˜o corrente do algoritmo de
a e ca
convers˜o de arestas gera um ou mais pixels na mesma linha de varredura que os pixels gerados an-
a
teriormente, os blocos devem ser atualizados se um novo pixel tem um valor de x m´ximo ou m´
a ınimo
mais extremo. Tratar casos de c´lculo de blocos para arestas que se cruzam, ou para slivers requer um
a
tratamento especial. Podemos calcular os blocos num passo, e preechˆ-los num segundo passo, ou calcu-
e
lar um bloco e preenchˆ-lo num unico passo. Outra vantagem de se utilizar blocos ´ que o processo de
e ´ e
clipping pode ser feito simultaneamente ao c´lculo dos blocos: os blocos podem ser recortados (clipped )
a
individualmente nas coordenadas esquerda e direita do retˆngulo de corte.
a
48

50. 1. Obt´m a menor coordenada y armazenada na ET; ou seja, o valor de y do primeiro “cesto”
e
n˜o vazio.
a
2. Inicializa a AET como vazia.
3. Repita at´ que a ET e a AET estejam vazias:
e
3.1. Transfere do cesto y na ET para a AET as arestas cujo ymin = y (lados que est˜o
a
come¸ando a serem varridos), mantendo a AET ordenada em x,
c
3.2. Retira os lados que possuem y = ymax (lados n˜o mais envolvidos nesta linha de
a
varredura,
3.3. Desenhe os pixels do bloco na linha de varredura y usando pares de coordenadas x da
AET.
3.4. Incremente y de 1 (coordenada da pr´xima linha de varredura).
o
3.5. Para cada aresta n˜o vertical que permanece na AET, atualiza x para o novo y.
a
3.6. Como o passo anterior pode ter desordenado a AET, reordena a AET.
Algoritmo 4.3: Algoritmo de convers˜o de arestas baseado na coerˆncia de arestas.
a e
49

51. Cap´
ıtulo 5
Transforma¸˜es 2D e 3D
co
Transforma¸˜es Geom´tricas (TG) s˜o a base de in´meras aplica¸˜es gr´ficas, podendo estar desde em
co e a u co a
simples programas para representar layouts de circuitos eletrˆnicos; em programas de planejamento de
o
cidades, onde pode-se usar movimentos de transla¸˜o para colocar os s´
ca ımbolos que definem edif´ ıcios e
a
´rvores em seus devidos lugares, rota¸˜es para orientar corretamente esses s´
co ımbolos, e altera¸˜o de escala
ca
para adequar o tamanho desses s´ ımbolos; ou mesmo em sistemas de software sofisticados que permitem
a constru¸˜o de cenas realistas.
ca
5.1 Transforma¸˜es em 2D
co
Primeiramente estudaremos as transforma¸˜es Geom´tricas em duas dimens˜es. Pode-se efetuar a Transla¸˜o
co e o ca
de pontos no plano (x, y) adicionando-se quantidades inteiras as suas coordenadas. Assim, cada ponto
P (x, y) pode ser movido por dx unidades em rela¸˜o ao eixo x, e por dy unidades em rela¸˜o ao eixo y.
ca ca
Logo, o ponto P (x , y ), pode ser escrito como:
x = x + dx
y = y + dy (5.1)
E se definimos os vetores colunas:
x
P =
y
x
P =
y
dx
T = (5.2)
dy
ent˜o a transla¸˜o, expressa pela Equa¸˜es , pode ser definida como:
a ca co
P =P +T (5.3)
Podemos transladar um objeto, fazendo-o a todos os seus pontos (o que n˜o ´ muito eficiente). Para
a e
transladar uma linha podemos fazˆ-lo apenas para seus pontos limites e sobre estes pontos redesenhar a
e
linha. Isso tamb´m ´ verdade para altera¸˜es de Escala e Rota¸˜o. Na Figura 5.1 ´ mostrado o efeito de
e e co ca e
uma transla¸˜o de um objeto por (3, −4).
ca
Pode-se efetuar Mudan¸as de Escala (ou apenas Escala) de um ponto pelo eixo x (sx), ou pelo eixo y
c
(sy), atrav´s das multiplica¸˜es:
e co
x = sx .x
y = sy .y (5.4)
Ou em forma matricial:
x sx 0 x
P =S·P ⇒ = · (5.5)
y 0 sy y
50

52. Figura 5.1: Transla¸˜o de uma casa.
ca
Figura 5.2: Mudan¸a de escala de uma casa. Como a escala ´ n˜o uniforme, sua propor¸˜o ´ alterada.
c e a ca e
Na figura 5.2 a casa sofre uma escala de 1 em x e de 1 em y.
2 4
Observe que a escala ´ feita em rela¸˜o a origem. Assim a casa fica menor e mais pr´xima da origem.
e ca o
Tamb´m as propor¸˜es da casa s˜o alteradas, isto ´, uma escala em que sx ´ diferente de sy . Por´m ao
e co a e e e
utilizar-se escalas uniformes (sx = sy ) as propor¸˜es n˜o s˜o afetadas.
co a a
A Rota¸˜o de pontos atrav´s de um ˆngulo θ qualquer tamb´m ´ feita a partir da origem. A rota¸˜o
ca e a e e ca
´ definida matematicamente por:
e
x = x. cos(θ) − y. sin(θ)
y = x. sin(θ) + y. cos(θ) (5.6)
e matricialmente:
x cos θ − sin θ x
P =R·P ⇒ = · (5.7)
y sin θ cos θ y
Escala e Rota¸˜o a partir de qualquer ponto ser˜o tratadas posteriormente.
ca a
Os ˆngulos positivos s˜o definidos quando a rota¸˜o ´ feita no sentido contr´rio aos do ponteiro do
a a ca e a
rel´gio, e ˆngulos negativos quando a rota¸˜o ´ feita no sentido dos ponteiros do rel´gio. Lembremos que
o a ca e o
sin(−θ) = − sin(θ) e que cos(−θ) = cos(θ).
Observando a Figura 5.4 vemos que a rota¸˜o por θ transforma P (x, y) em P (x , y ). Como a rota¸˜o
ca ca
´ em rela¸˜o a origem, as distˆncias de P e P a origem, r na figura, s˜o iguais. Assim, temos que:
e ca a a
x = r. cos(φ)
y = r. sin(φ) (5.8)
x = r · cos(θ + φ) = r. cos(φ). cos(θ) − r. sin(φ) sin(θ)
y = r · sin(θ + φ) = r cos(φ) sin(θ) + r. sin(φ). cos(θ) (5.9)
Podemos obter a Equa¸˜o 5.6, substituindo a Equa¸˜o 5.8 na Equa¸˜o 5.9.
ca ca ca
51

53. Figura 5.3: Esta figura mostra a rota¸ao da casa por 45◦ . Da mesma forma que para a escala, a rota¸˜o
c˜ ca
tamb´m ´ feita em rela¸˜o a origem.
e e ca
Figura 5.4: Derivando a equa¸˜o de rota¸˜o.
ca ca
5.2 Coordenadas Homogˆneas e Matrizes de Transforma¸˜o
e ca
Para a Transla¸˜o, Escala e Rota¸˜o, as matrizes de transforma¸˜o s˜o respectivamente:
ca ca ca a
P =T +P (5.10)
P =S·P (5.11)
P =R·P (5.12)
Infelizmente, a transla¸˜o ´ tratada de forma diferente (como uma soma) das outras - Rota¸˜o e
ca e ca
Escala - que s˜o tratadas atrav´s de multiplica¸˜es. Para que possamos combinar facilmente essas trans-
a e co
forma¸˜es, devemos poder tratar do mesmo modo todas as 3 transforma¸˜es de uma forma consistente.
co co
Se os pontos s˜o expressos em Coordenadas Homogˆneas, todas as 3 transforma¸˜es podem ser tra-
a e co
tadas como multiplica¸˜es.
co
Em coordenadas homogˆneas, adicionamos uma terceira coordenada ao ponto. Logo, em vez de
e
um ponto ser representado por um par de valores (x, y), ele ´ representado por uma tripla (x, y, W ).
e
Dizemos que 2 conjuntos de coordenadas homogˆneas (x, y, W ) e (x , y , W ) representam o mesmo ponto
e
se e somente se um ´ m´ltiplo do outro. Assim, (2, 3, 6) e (4, 6, 12) ´ o mesmo ponto representado por
e u e
diferentes triplas. Isto ´, cada ponto tem muitas diferentes representa¸˜es homogˆneas. Tamb´m, pelo
e co e e
menos uma das coordenadas homogˆneas precisa ser diferente de zero, assim (0, 0, 0) n˜o ´ permitido.
e a e
x y
Se W ´ a coordenada n˜o zero, podemos dividir (x, y, W ) por ela, obtendo o mesmo ponto ( W , W , 1).
e a
x y
Os n´meros W e W s˜o chamados de Coordenadas Cartesianas do ponto homogˆneo. Usualmente, triplas
u a e
representam pontos em um espa¸o 3D, mas agora est˜o sendo usadas para representar pontos em 2D.
c a
Observemos que, se tomarmos todas as triplas que representam o mesmo ponto, isto ´, todas as triplas
e
da forma (tx, ty, tW ) com t diferente de 0, obtemos uma linha no espa¸o 3D. Se homogeneizamos o ponto
c
(dividimos por W ), obtemos um ponto da forma (x, y, 1). Logo, os pontos homogeneizados formam o
plano definido pela equa¸˜o W = 1 no espa¸o (x, y, W ). A Figura 5.5, mostra esse relacionamento. Como
ca c
agora os pontos s˜o vetores de 3 elementos, as matrizes de transforma¸˜es que multiplicam um ponto por
a co
outro tamb´m precisam ser de 3x3. A equa¸˜o de Transla¸˜o 5.1 para coordenadas homogˆneas fica:
e ca ca e
52

54. Figura 5.5: O espa¸o de Coordenadas Homogˆneas XY W , com o plano W = 1 e o ponto P (X, Y, W )
c e
projetado sobre o plano W = 1.
     
x 1 0 dx x
 y  =  0 1 dy  ·  y  (5.13)
1 0 0 1 1
Assim, a equa¸˜o 5.13 pode ser representada como:
ca
P = T (dx , dy ) · P (5.14)
onde:
 
1 0 dx
T (dx , dy ) =  0 1 dy  (5.15)
0 0 1
O que acontece se um ponto P ´ transladado por T (dx1 , dy1 ) para P’ e ent˜o transladado por
e a
T (dx2 , dy2 ) para P ?
Intuitivamente esperamos que essas transla¸˜es sejam equivalentes a T (dx1 + dx2 , dy1 + dy2 ). Ou seja,
co
se:
P = T (dx1 , dy1 ) · P (5.16)
P = T (dx2 , dy2 ) · P (5.17)
(5.18)
Substituindo 5.17 em 5.18, temos:
P = T (dx2 , dy2 ) · [T (dx1 , dy1 ) · P ] = [T (dx2 , dy2 ) · T (dx1 , dy1 )] · P (5.19)
e a matriz produto das matrizes T (dx2 , dy2 ) · T (dx1 , dy1 ), ´:
e
     
1 0 dx2 1 0 dx1 1 0 dx1 + dx2
 0 1 dy2  ·  0 1 dy1  =  0 1 dy1 + dy2  (5.20)
0 0 1 0 0 1 0 0 1
e vemos que a Transla¸˜o ´ aditiva.
ca e
Essa transforma¸˜o expressa pelas duas transforma¸˜es, ´ chamada de Transforma¸˜o de Composi¸˜o.
ca co e ca ca
Podemos mostrar similarmente que podemos realizar Composi¸˜es tamb´m com a Escala e a Rota¸˜o.
co e ca
Assim, as equa¸˜es de Escala 5.4, s˜o representadas matricialmente:
co a
53

55.      
x sx 0 0 x
y  =  0 sy 0 · y  (5.21)
1 0 0 1 1
e definindo,
 
sx 0 0
S(sx , sy ) =  0 sy 0 (5.22)
0 0 1
temos
P = S(sx1 , sy1 ) · P (5.23)
P = S(sx2 , sy2 ) · P (5.24)
e substituindo:
P = S(sx2 , sy2 ) · [S(sx1 , sy1 ) · P ] = [S(sx2 , sy2 ).S(sx1 , sy1 )] · P (5.25)
A matriz produto S(sx2 , sy2 ) · S(sx1 , sy1 ) ´:
e
     
sx2 0 0 sx1 0 0 sx1 .sx2 0 0
 0 sy2 0  ·  0 sy1 0 =  0 sy1 .sy2 0 (5.26)
0 0 1 0 0 1 0 0 1
e temos que a Escala ´ multiplicativa.
e
Finalmente, verifiquemos como ficam as equa¸˜es de rota¸˜o:
co ca
     
x cos θ − sin θ 0 x
 y  =  sin θ cos θ 0 · y  (5.27)
1 0 0 1 1
Definindo:
 
cos θ − sin θ 0
R(θ) =  sin θ cos θ 0 (5.28)
0 0 1
temos que:
P = R(θ) · P (5.29)
Como exerc´
ıcio, mostre que duas rota¸˜es s˜o aditivas!
co a
Figura 5.6: Um cubo unit´rio ´ rodados 45 graus, posteriormente escalado n˜o uniformemente. Obtem-se
a e a
dessa forma uma transforma¸˜o afim.
ca
54

56. Uma sequˆncia arbitr´ria de rota¸oes, transla¸˜es e escalas, s˜o chamadas de transforma¸˜es afins.
e a c˜ co a co
As Transforma¸˜es Afins preservam paralelismo de linhas, mas n˜o comprimentos e ˆngulos. A figura
co a a
5.6, mostra o resultado de se aplicar uma rota¸˜o de 45◦ e depois uma escala n˜o uniforme a um cubo
ca a
unit´rio.
a
Uma matriz de transforma¸˜o da forma:
ca
 
r11 r12 tx
M =  r21 r22 ty  (5.30)
0 0 1
onde a submatriz 2x2 do canto superior esquerdo ´ ortogonal, preserva ˆngulos e comprimentos. Estas
e a
transforma¸˜es s˜o chamadas de Corpo R´
co a ıgido, porque o corpo do objeto n˜o ´ distorcido de forma
a e
alguma.
5.3 Transforma¸˜es 2D Adicionais: Espelhamento e Shearing
co
Duas transforma¸˜es adicionais bastante usadas em CG s˜o o Espelhamento (Reflex˜o) e Distor¸˜o
co a a ca
(Shearing), discutidas a seguir.
5.3.1 Espelhamento (Mirror)
A transforma¸˜o de reflex˜o, ou espelhamento, aplicada a um objeto, produz um objeto que ´ o espelho do
ca a e
original. No caso de uma reflex˜o 2D, o espelho ´ gerado relativamente a um eixo de reflex˜o rotacionando
a e a
o objeto de 180o em torno do eixo de reflex˜o. Por exemplo, pode-se aplicar uma reflex˜o em torno da
a a
linha y = 0 (o eixo x) usando a seguinte matriz de transforma¸˜o:
ca
 
1 0 0
M irrorv =  0 −1 0 (5.31)
0 0 1
Esta transforma¸˜o mant´m as coordenadas x do objeto inalteradas, mas “inverte” os valores das
ca e
coordenadas y, alterando a orienta¸˜o espacial do objeto.
ca
Analogamente, poder´ ıamos definir uma reflex˜o em torno do eixo y, que “inverteria” as coordenadas
a
x do objeto.
Figura 5.7: Reflex˜o de um objeto em torno do eixo x.
a
Podemos tamb´m definir uma reflex˜o em torno de um eixo perpendicular ao plano xy e passando
e a
(por exemplo) pela origem do sistema de coordenadas, “invertendo” nesse caso ambas as coordenadas x
e y. A matriz de transforma¸˜o ´ dada por:
ca e
 
−1 0 0
M irrorxy =  0 −1 0  (5.32)
0 0 1
55

57. A opera¸˜o ´ ilustrada na figura 5.8. Observe que a matriz de reflex˜o acima ´ idˆntica ` matriz de
ca e a e e a
rota¸˜o R(θ) com θ = 180o , ou seja, estamos t˜o somente rotacionando o objeto de 180o em torno da
ca a
origem. A opera¸˜o pode ser generalizada para adotar qualquer ponto de reflex˜o localizado no plano
ca a
xy, e o efeito ´ o mesmo que aplicar uma rota¸˜o de 180o em torno do ponto pivˆ da reflex˜o.
e ca o a
Figura 5.8: Reflex˜o de um objeto em torno de um eixo perpendicular ao plano xy, passando pela origem.
a
Podemos tamb´m adotar um eixo de reflex˜o arbitr´rio. A matriz de reflex˜o pode ser derivada pela
e a a a
concatena¸˜o de uma seq¨ˆncia de matrizes de reflex˜o e de rota¸˜o. Por exemplo, se a reflex˜o for em
ca ue a ca a
torno da linha diagonal definida por y = x, a matriz de reflex˜o pode ser derivada da combina¸˜o da
a ca
seguinte seq¨ˆncia de transforma¸˜es:
ue co
1. rota¸˜o de 45o na dire¸˜o hor´ria para fazer a linha y = x coincidir com o eixo x.
ca ca a
2. reflex˜o em torno do eixo x.
a
3. rota¸˜o de 45o na dire¸˜o anti-hor´ria para retomar a orienta¸˜o original da linha y = x.
ca ca a ca
5.3.2 Shearing
Shearing (cisalhamento) ´ uma transforma¸˜o que distorce o formato de um objeto - em geral, ´ aplicado
e ca e
um deslocamento aos valores das coordenadas x ou das coordenadas y do objeto. Uma distor¸˜o na ca
dire¸˜o x ´ produzida com a seguinte matriz de transforma¸˜o:
ca e ca
 
1 shx 0
Shearx =  0 1 0 (5.33)
0 0 1
As coordenadas do objeto s˜o transformadas da seguinte maneira:
a
x = x + shx y
y =y (5.34)
Qualquer n´mero real pode ser usado como parˆmetro. O resultado ´ que as coordenadas (x, y) s˜o
u a e a
deslocadas horizontalmente segundo um valor proporcional ` sua distˆncia em do eixo x. Por exem-
a a
plo, se shx ´ 2, um quadrado ser´ transformado em um paralelogramo. Valores negativos deslocam as
e a
coordenadas para a esquerda.
Pode-se gerar distor¸˜es na dire¸˜o relativamente a outros eixos de referˆncia y = yref com a matriz:
co ca e
 
1 shx −shx .yref
Shearyref = 0 1 0  (5.35)
0 0 1
que produz as seguintes transforma¸˜es sobre as coordenadas:
co
56

58. x = x + shx (y − yref )
y =y (5.36)
Analogamente, pode-se aplicar uma distor¸˜o na dire¸˜o y, relativa a uma linha x = xref, usando
ca ca
 
1 0 0
Shearxref =  shy 1 −shy .xref  (5.37)
0 0 1
que gera as seguintes transforma¸˜es nas posi¸˜es das coordenadas:
co co
x =x
y = y + shy .(x − xref ). (5.38)
Esta transforma¸˜o desloca as coordenadas de uma posi¸˜o verticalmente segundo um fator propor-
ca ca
cional ` sua distˆncia da linha de referˆncia x = xref . Qualquer opera¸˜o de distor¸˜o pode ser descrita
a a e ca ca
como uma composi¸˜o de transforma¸oes envolvendo uma seq¨ˆncia de matrizes de rota¸˜o e escala.
ca c˜ ue ca
5.4 Transforma¸˜es entre sistemas de coordenadas
co
J´ vimos que aplica¸˜es gr´ficas freq¨entemente requerem a transforma¸˜o de descri¸˜es de objetos de um
a co a u ca co
sistema de coordenadas para outro. Muitas vezes, o objeto ´ descrito em um sistema de coordenadas n˜o
e a
Cartesiano (como coordenadas polares ou el´ ıpticas), e precisa ser convertido para o sistema de coordenadas
Cartesiano do dispositivo. Em aplica¸˜es de design e modelagem, objetos individuais s˜o definidos em
co a
seu pr´prio sistema de coordenadas, e as coordenadas locais devem ser transformadas para posicionar
o
os objetos no sistema de coordenadas global da cena. Neste texto vamos considerar especificamente
transforma¸˜es entre dois sistemas de coordenadas Cartesianos.
co
Para transformar descri¸˜es de um objeto dadas em um sistema de coordenadas xy para um sistema
co
x y com origens em (0, 0) e (x0 , y0 ), com um ˆngulo de orienta¸˜o θ entre os eixos x e x , precisamos
a ca
determinar a transforma¸˜o que superp˜e os eixos xy aos eixos x y . Isso pode ser feito em 2 passos:
ca o
1. transladar o sistema x y de modo que sua origem coincida com a origem do sistema xy: T (−x0 , −y0 )
2. Rotacionar o eixo x de forma que ele coincida com o eixo x: R(−θ)
Concatenando as duas matrizes de transforma¸˜o obt´m-se a matriz de composi¸˜o que descreve a
ca e ca
transforma¸˜o necess´ria:
ca a
Mxy,x y = R(−θ) · T (−x0 , −y0 ) (5.39)
Um m´todo alternativo para estabelecer a orienta¸˜o do segundo sistema de coordenadas consiste em
e ca
especificar um vetor V na dire¸˜o positiva do eixo y , passando pela origem do sistema xy. O vetor V ´
ca e
especificado como um ponto no sistema de referˆncia xy em rela¸˜o ` origem do sistema xy. Um vetor
e ca a
unit´rio que d´ a dire¸˜o de y pode ent˜o ser obtido:
a a ca a
V
v= = (vx , vy ) (5.40)
|V |
E obtemos o vetor unit´rio u ao longo do eixo x rotacionando v de 90o no sentido hor´rio:
a a
u = (vy , −vx ) = (ux , uy ) (5.41)
J´ vimos que os elementos de uma matriz de rota¸˜o podem ser expressos como elementos de um
a ca
conjunto de vetores ortogonais. Portanto, a matriz de rota¸˜o a ser usada para rotacionar o sistema x y
ca
para que este coincida com o sistema xy ´ dada por:
e
57

59.  
ux uy 0
R =  vx vy 0 (5.42)
0 0 1
Por exemplo, se escolhermos que a nova orienta¸˜o deve ser dada pelos vetores U = (0, 1) (eixo y
ca
positivo no sistema atual) e V = (−1, 0) (eixo x negativo no sistema atual), a matriz de rota¸˜o ´ dada
ca e
por:
 
0 1 0
R =  −1 0 0 (5.43)
0 0 1
Essa matriz ´ equivalente ` matriz de rota¸˜o para θ = 90o
e a ca
5.5 Composi¸˜o de Transforma¸˜es
ca co
Usaremos composi¸˜o como uma combina¸˜o de matrizes de transforma¸˜o R, S e T. O prop´sito de
ca ca ca o
compor-se transforma¸˜es, ´ o ganho de eficiˆncia que se obt´m ao aplicar-se uma transforma¸˜o composta
co e e e ca
a um ponto em vez de aplicar-lhe uma s´rie de transforma¸˜es, uma ap´s a outra.
e co o
Considerando a rota¸˜o de um objeto em torno de um ponto arbitr´rio P 1. Mas sabemos apenas
ca a
rotacionar um ponto em rela¸˜o a origem. Assim, podemos dividir este problema de rota¸˜o em 3
ca ca
problemas simples, ou seja: para rotacionar em rela¸˜o a P 1, pode-se usar a seguinte sequˆncia de
ca e
transforma¸˜es fundamentais:
co
1. Efetuar uma transla¸˜o, levando P 1 ` origem.
ca a
2. Efetuar a Rota¸˜o desejada.
ca
3. Efetuar uma Transla¸˜o oposta ` realizada em (1), levando P 1 a posi¸˜o anterior.
ca a ca
Figura 5.9: Rota¸˜o em rela¸˜o ao Ponto P 1, por um ˆngulo θ.
ca ca a
Esta sequˆncia ´ ilustrada na figura 5.9, onde a casa ´ rotacionada em rela¸˜o a P1 (x1 , y1 ). A primeira
e e e ca
transla¸˜o ´ por (−x1 , −y1 ), e a ultima transla¸˜o (oposta a primeira) ´ por (x1 , y1 ). A transforma¸˜o
ca e ´ ca e ca
em sequˆncia ´:
e e
     
1 0 x1 cos θ − sin θ 0 1 0 −x1
T (x1 , y1 ) · R(θ) · T (x1 , y1 ) =  0 1 y1  ·  sin θ cos θ 0  ·  0 1 −y1  =
0 0 1 0 0 1 0 0 1
 
cos θ − sin θ x1 (1 − cos θ) + y1 . sin θ
 sin θ cos θ y1 (1 − cos θ) + x1 . sin θ  (5.44)
0 0 1
Esse procedimento pode ser usado de forma similar para se efetuar a Escala de um objeto em rela¸˜o
ca
a um ponto arbitr´rio P1 . Primeiramente o ponto P1 ´ transladado para a origem, ent˜o ´ feita a escala
a e a e
desejada, e ent˜o o ponto P1 ´ transladado de volta. Dessa forma, a transforma¸˜o em seq¨ˆncia ´:
a e ca ue e
58

60.      
1 0 x1 sx 0 0 1 0 −x1
T (x1 , y1 ) · S(sx , sy ) · T (x1 , y1 ) =  0 1 y1  ·  0 sy 0  ·  0 1 −y1  =
0 0 1 0 0 1 0 0 1
 
sx 0 x1 (1 − sx )
 0 sy y1 (1 − sy )  (5.45)
0 0 1
Suponhamos que desejamos escalar, rotacionar e posicionar a casa mostrada na figura 5.10, com o
ponto P 1(x1 , y1 ) como o centro da rota¸˜o e da escala. A seq¨ˆncia de transforma¸˜es fica a seguinte:
ca ue co
1. Transladar P 1(x1 , y1 ) para a origem;
2. Efetuar a escala e a rota¸˜o desejadas;
ca
3. Efetuar a transla¸˜o da origem para a nova posi¸˜o P 2(x2 , y2 ), onde a casa deve ser posicionada.
ca ca
T (x2 , y2 ) · R(θ) · S(sx , sy ) · T (−x1 , −y1 ) ´ a matriz da Transforma¸˜o composta.
e ca
Figura 5.10: Escala e rota¸˜o de uma casa em rela¸˜o ao ponto P1 .
ca ca
Se M 1 e M 2 representam duas transforma¸˜es fundamentais (transla¸˜o, rota¸˜o ou escala), em que
co ca ca
casos M 1 · M 2 = M 2 · M 1? Isto ´, quando suas matrizes de transforma¸˜o comutam? Sabemos que
e ca
geralmente a multiplica¸˜o de matrizes n˜o ´ comutativa. Entretanto ´ f´cil mostrar que nos seguintes
ca a e e a
casos especiais esta comutatividade existe (Tabela 5.1).
m1 M2
Transla¸˜o
ca Transla¸˜o
ca
Escala Escala
Rota¸˜o
ca Rota¸˜o
ca
Escala(s, s) Rota¸˜o
ca
Tabela 5.1: Transforma¸˜es comutativas.
co
Nestes casos n˜o precisamos estar atentos a ordem de constru¸˜o da matriz de transforma¸˜o.
a ca ca
5.6 Transforma¸˜o Janela - Porta de Vis˜o (“Window-to-Viewport”)
ca a
Alguns sistemas gr´ficos permitem ao programador especificar primitivas de sa´ em um sistema de
a ıda
coordenadas em ponto-flutuante, chamado de sistema de coordenadas do Mundo Real, usando a unidade
de medida que melhor se adeque ao seu programa de aplica¸˜o (angstrons, microns, metros, anos-luz,
ca
etc.). O termo Mundo (World ) ´ usado para representar o ambiente interativamente criado ou apresentado
e
para o usu´rio. Como as primitivas s˜o especificadas em coordenadas do mundo, o pacote gr´fico precisa
a a a
mapear as coordenadas do mundo em coordenadas de tela.
Uma forma de se efetuar esta transforma¸˜o ´ especificando uma regi˜o retangular em coordenadas
ca e a
do mundo, chamada de janela de coordenadas do mundo, e uma regi˜o retangular correspondente em
a
coordenadas de tela, chamada de Porta de Vis˜o (Viewport), em que a janela em coordenadas do mundo
a
real ´ mapeada. A transforma¸˜o que mapeia a janela na porta de vis˜o ´ aplicada a todas as primitivas
e ca a e
de sa´ em coordenadas do mundo, mapeando-as na tela. Este procedimento ´ ilustrado na Figura 5.11.
ıda e
Como pode ser visto pela figura, se a janela e a porta de vis˜o n˜o possuem a mesma raz˜o largura-altura,
a a a
uma escala n˜o uniforme ´ realizada. Se o programa de aplica¸˜o altera a janela ou a porta de vis˜o,
a e ca a
59

61. Figura 5.11: Janela em Coordenadas do mundo e porta de vis˜o em coordenadas de tela.
a
Figura 5.12: Duas portas de vis˜o associadas a mesma janela.
a
ent˜o as novas primitivas de sa´ desenhadas sobre a tela precisam ser tamb´m atualizadas. Outro ponto
a ıda e
´ que pode-se ter m´ltiplas portas de vis˜o de uma mesma janela, o que ´ mostrado na Figura 5.12.
e u a e
Dada uma janela e uma porta de vis˜o, qual ´ a matriz de transforma¸˜o que mapeia a janela em
a e ca
coordenadas do mundo real, na porta de vis˜o em coordenadas de tela? Esta matriz pode ser desenvolvida
a
como uma transforma¸˜o composta por 3 passos, como ´ sugerido na Figura 5.11. A janela especificada
ca e
pelo seu canto inferior esquerdo e canto superior direito, ´ primeiramente transladada para a origem do
e
mundo de coordenadas. A seguir o tamanho da janela ´ escalonado para ser igual ao tamanho da porta
e
de vis˜o. Finalmente, a transla¸˜o ´ usada para posicionar a porta de vis˜o. A matriz global Mjp ´:
a ca e a e
umax − umin vmax − vmin
Mjp = T (umin , vmin ) · S( , ) · T (−xmin , −ymin ) =
xmax − xmin ymax − ymin
   umax −umin   
1 0 umin xmax −xmin 0 0 1 0 −xmin
 0 1 vmin  ·  vmax −vmin
0 ymax −ymin 0  ·  0 1 −ymin  =
0 0 1 0 0 1 0 0 1
 umax −umin umax −umin 
xmax −xmin 0 −xmin . xmax −xmin + umin
vmax −vmin
 0 ymax −ymin −ymin . ymax −vmin + vmin 
v
max −ymin
(5.46)
0 0 1
 
x
Multiplicando P = Mjp ·  y , temos:
1
(x − xmin ). umax −umin + umin
 min

xmax −x
v −v
P =  (y − ymin ). ymax −ymin + vmin  · (5.47)
max min
1
Muitos pacotes gr´ficos combinam a transforma¸˜o janela - porta de vis˜o com recorte (clipping) de
a ca a
primitivas gr´ficas de sa´
a ıda. A figura 10.14 ilustra esta t´cnica de recorte.
e
60

62. Figura 5.13: Os passos da transforma¸˜o janela - porta de vis˜o.
ca a
Figura 5.14: Primitivas gr´ficas de sa´ em coordenadas do mundo s˜o recortadas pela janela. O seu
a ıda a
interior ´ apresentado na tela (viewport).
e
5.7 Eficiˆncia
e
Uma composi¸˜o gen´rica de transforma¸˜es R, S e T , produz uma matriz da forma:
ca e co
 
r11 r12 tx
M =  r21 r22 ty  (5.48)
0 0 1
A submatriz 2x2 superior esquerda, ´ uma composi¸˜o das matrizes de rota¸˜o e escala, enquanto tx e
e ca ca
ty s˜o obtidos por influˆncia da transla¸˜o. Ao calcularmos M · P (um vetor de 3 elementos multiplicado
a e ca
por uma matriz 3x3), verificamos que s˜o necess´rias 9 multiplica¸˜es e 6 adi¸˜es. Mas, como a ultima
a a co co ´
linha da matriz ´ fixa, os c´lculos efetivamente necess´rios s˜o:
e a a a
x = x.r11 + y.r12 + tx
y = x.r21 + y.r22 + ty (5.49)
o que reduz o processo a quatro multiplica¸˜es e duas adi¸˜es, o que ´ um ganho significante em termos
co co e
de eficiˆncia. Especialmente se considerarmos que esta opera¸˜o deve ser aplicada a centenas ou mesmo
e ca
milhares de pontos por cena ou figura.
Outra ´rea onde a eficiˆncia ´ muito importante ´ na cria¸˜o de sucessivas vis˜es de um objeto,
a e e e ca o
tal como por exemplo vis˜es consecutivas de sistemas de mol´culas, avi˜es, etc., onde cada vis˜o ´
o e o a e
geralmente rotacionada a poucos graus da vis˜o anterior. Se cada vis˜o pode ser gerada e apresentada
a a
de forma bastante r´pida (30 a 100 milisegundos cada uma), ent˜o parecer´ ao observador que o objeto
a a a
est´ sendo rotacionado continuamente (efeito de anima¸˜o!). Para conseguirmos isto, devemos efetuar as
a ca
transforma¸˜es sobre os pontos do objeto o mais rapidamente poss´
co ıvel. As equa¸˜es de rota¸˜o (Equa¸˜o
co ca ca
5.8) requerem 4 multiplica¸˜es e 2 adi¸˜es. Mas se θ ´ pequeno (poucos graus), cos θ ´ quase 1. Dessa
co co e e
aproxima¸˜o, temos que:
ca
x = x − y. sin θ
61

63. y = x . sin θ + y (5.50)
sin −θ = − sin θ (5.51)
que requer 2 multiplica¸˜es e 2 adi¸˜es (livranos de 2 multiplica¸˜es pode ser muito importante em
co co co
computadores sem hardware espec´ ıfico para isto!).
A Equa¸˜o 5.50, ´ somente uma aproxima¸˜o para os valores corretos de x e y (existe um erro
ca e ca
embutido!). Cada vez que a f´rmula ´ aplicada a novos valores de x e y o erro torna-se um pouquinho
o e
maior. Uma aproxima¸˜o melhor ´ usar x em vez de x na segunda equa¸˜o:
ca e ca
x = x = y. sin θ
y = x . sin θ + y = (x − y. sin θ). sin θ + y = x. sin θ + y.(1 − sin2 θ) (5.52)
Esta ´ uma melhor aproxima¸˜o que a equa¸˜o 5.50, porque o determinante da matriz 2x2 correspon-
e ca ca
dente ´ 1, o que significa que as ´reas transformadas pela equa¸˜o 5.52n˜o s˜o alteradas.
e a ca a a
62

64. Eixo de Rota¸˜o
ca Dire¸˜o da Rota¸˜o Positiva
ca ca
x y para z
y z para x
z x para y
Tabela 5.2: Sentido de rota¸˜o.
ca
5.8 Transforma¸˜es em 3D
co
A capacidade para representar e visualizar um objeto em trˆs dimens˜es ´ fundamental para a percep¸˜o
e o e ca
de sua forma. Por´m, em muitas situa¸˜es ´ necess´rio mais do que isto, ou seja, poder “manusear” o
e co e a
objeto, movimentando-o atrav´s de rota¸˜es, transla¸˜es e mesmo escala.
e co co
Assim, generalizando o que foi visto para TG em 2D, onde estas transforma¸˜es foram representadas
co
por matrizes 3x3 (utilizando coordenadas homogˆneas), as TGs em 3D ser˜o representadas por matrizes
e a
4x4 tamb´m em coordenadas homogˆneas.
e e
Dessa forma, um ponto P de coodenadas (x, y, z) ser´ representado por (x, y, z, W ). Padronizando
a
x y z
(ou homogeneizando) o ponto, teremos se w for diferente de 0, ( W , W , W , 1).
Figura 5.15: Sistema de Coordenadas dado pela Regra da M˜o Direita.
a
O sistema de coordenadas para 3D utilizado ser´ o da Regra da M˜o Direita, com o eixo Z perpen-
a a
dicular ao papel e saindo em dire¸˜o ao observador, como poder ser visto na figura 5.15.
ca
O sentido positivo de uma rota¸˜o, ´ dado quando observando-se sobre um eixo positivo em dire¸˜o
ca e ca
` origem, uma rota¸˜o de 90◦ ir´ levar um eixo positivo em outro positivo. Ou conforme a Tabela 5.2.
a ca a
A Regra da M˜o Direita foi escolhida porque este ´ o padr˜o utilizado na matem´tica (lembre-se da
a e a a
defini¸˜o do produto vetorial!).
ca
¸˜
A TRANSLACAO em 3D pode ser vista como simplesmente uma exten¸˜o a partir da transla¸˜o 2D,
ca ca
ou seja:
x 1 0 0 dx x
     
 y   0 1 0 dy   y 
 = ·  (5.53)
z 0 0 1 dz z
1 0 0 0 1 1
Assim, a Equa¸˜o 5.53 pode ser representada tamb´m como:
ca e
P = T (dx , dy , dz ) · P (5.54)
Similarmente a ESCALA em 3D, fica:
x sx 0 0 0 x
     
y   0 sy 0 0 y 
 = ·  (5.55)

z 0 0 sz 0 z
1 0 0 0 1 1
P = S(sx , sy , sz ) · P (5.56)
63

65. co ¸˜
Finalmente, verifiquemos como ficam as equa¸˜es de ROTACAO em 3D, pois as rota¸˜es podem ser
co
efetuadas em rela¸˜o a qualquer um dos trˆs eixos.
ca e
A equa¸˜o de rota¸˜o em 2D ´ justamente uma rota¸˜o em torno do eixo z em 3D, a qual ´:
ca ca e ca e
x cos θ − sin θ 0 0 x
     
 y   sin θ cos θ 0 0 y 
 = ·  (5.57)
z 0 0 1 0 z
1 0 0 0 1 1
A matriz de rota¸˜o em rela¸˜o ao eixo x ´:
ca ca e
x 1 0 0 0 x
     
y  0 cos θ − sin θ 0 y 
 = ·  (5.58)
z 0 sin θ cos θ 0 z
1 0 0 0 1 1
A matriz de rota¸˜o em rela¸˜o ao eixo y ´:
ca ca e
x cos θ 0 sin θ 0 x
     
y   0 1 0 0 y 
 = ·  (5.59)
z − sin θ 0 cos θ 0 z
1 0 0 0 1 1
Para a rota¸˜o tamb´m temos que:
ca e
P = R(θ) · P (5.60)
OBS: Os vetores compostos pelas linhas e colunas da submatriz 3x3 do canto superior esquerdo de
Rx,y,z (θ) s˜o mutuamente perpendiculares, e a submatriz possui determinante igual a 1, o que significa
a
que as trˆs matrizes s˜o chamadas de Ortogonais Especiais. Al´m disso, uma sequˆncia arbitr´ria
e a e e a
de rota¸˜es ´ tamb´m ortogonal especial. Deve-se lembrar que as transforma¸˜es ortogonais preservam
co e e co
distˆncias e ˆngulos.
a a
Todas estas matrizes de transforma¸˜o (T, SeR) possuem inversas. A inversa de T ´ obtida simples-
ca e
mente negando-se dx , dy e dz . Para a matriz S, basta substituir sx , sy e sz por seus valores inversos.
Para cada uma das matrizes de rota¸˜o R, basta negar o ˆngulo de rota¸˜o. Al´m disso, para uma matriz
ca a ca e
ortogonal B, sua inversa (B −1 ) ´ a sua matriz transposta, ou seja B −1 = B T .
e
Uma sequˆncia arbitr´ria de transforma¸˜es de transla¸˜o, escala e rota¸˜o podem ser multiplicadas
e a co ca ca
juntas, resultando uma matriz da seguinte forma:
r11 r12 r13 tx
 
 r21 r22 r23 ty 
M = (5.61)
r31 r32 r33 tz

0 0 0 1
Como no caso de 2D, a submatriz 3x3 do canto superior esquerdo R, agrega as transforma¸˜es de
co
escala e rota¸˜o, enquanto a ultima coluna ` direita T agrega as transla¸˜es. Para obter-se um pouco
ca ´ a co
mais de eficiˆncia (ganho computacional) pode-se executar a transforma¸˜o explicitamente como:
e ca
x x
   
y  y
 =R· +T (5.62)
z z
1 1
5.8.1 Composi¸˜o de Transforma¸˜es em 3D
ca co
A composi¸˜o de transforma¸˜es em 3D pode ser entendida mais facilmente atrav´s do exemplo indicado
ca co e
na figura 5.16. O objetivo ´ transformar os segmentos de reta P1 P2 e P1 P3 da posi¸˜o inicial em (a) para
e ca
a posi¸˜o final em (b). Assim o ponto P1 deve ser transladado para a origem, P1 P2 dever´ ficar sobre
ca a
o eixo z positivo, e P 1P 3 dever´ ficar no plano positivo de yz. Al´m disso, os comprimentos das linhas
a e
n˜o devem ser alterados.
a
64

66. Figura 5.16: Transformando P1 , P2 e P3 da posi¸˜o inicial em (a) para a posi¸˜o final em (b).
ca ca
Uma primeira maneira de se obter a transforma¸˜o desejada ´ atrav´s da composi¸˜o das primitivas
ca e e ca
de transforma¸˜o T , Rx , Ry e Rz .
ca
Subdividindo o problema, teremos os seguintes quatro passos:
1. Transladar P1 para a origem.
2. Rotacionar o segmento P1 P2 em rela¸˜o ao eixo y, de forma que ele (P1 P2 ) fique no plano yz.
ca
3. Rotacionar o segmento P1 P2 em rela¸˜o ao eixo x, de forma que ele (P1 P2 ) fique sobre o eixo z.
ca
4. Rotacionar o segmento P1 P3 em rela¸˜o ao eixo z, de forma que ele (P1 P3 ) fique no plano yz.
ca
Primeiro Passo: Transladar P1 para a Origem
A equa¸˜o de transla¸˜o ´:
ca ca e
1 0 0 −x1
 
0 1 0 −y1 
T (−x1 , −y1 , −z1 ) =  (5.63)
0 0 1 −z1

0 0 0 1
Aplicando T a P1 , P2 e P3 , temos:
0
 
0
P1 = T (−x1 , −y1 , −z1 ) · P1 =  
0
1
x2 − x1
 
 y − y1 
P2 = T (−x1 , −y1 , −z1 ) · P2 =  2
z2 − z1

1
x3 − x1
 
 y − y1 
P3 = T (−x1 , −y1 , −z1 ) · P3 =  3 (5.64)
z3 − z1

1
Segundo Passo: Rotacionar em Rela¸˜o ao eixo Y
ca
A Figura 5.17 (o ˆngulo θ indica a dire¸˜o positiva de rota¸˜o em rela¸˜o a y. O ˆngulo utilizado na
a ca ca ca a
realidade ´ −(90o − θ)) mostra P1 P2 ap´s o primeiro passo, bem como a proje¸˜o de P1 P2 no plano xz.
e o ca
O ˆngulo de rota¸˜o ´ −(90o − θ) = θ − 90o . Ent˜o:
a ca e a
x2 x2 − x1
sin(θ − 90o ) = − cos θ = − =−
D1 D1
z2 z2 − z1
cos(θ − 90o ) = sin θ = − =− (5.65)
D1 D1
65

67. Figura 5.17: Rota¸˜o dos pontos P1 , P2 e P3 .
ca
onde
D1 = (z2 )2 + (x2 )2 = (z2 − z1 )2 + (x2 − x1 )2 (5.66)
Ent˜o substituindo estes valores na Equa¸˜o 5.59, temos:
a ca
0
 
 y − y1 
P2 = Ry (θ − 90o ) · P2 =  2 (5.67)
D1

1
Como era esperado, a componente x de P2 ´ zero, e z possui comprimento D1 .
e
Terceiro Passo: Rotacionar em Rela¸˜o ao eixo X
ca
Figura 5.18: Rota¸˜o em rela¸˜o ao eixo x. P1 e P2 de comprimento D2 ´ rotacionado em dire¸˜o ao
ca ca e ca
eixo z, pelo ˆngulo positivo f.
a
A Figura 5.18 mostra P1 P2 ap´s o segundo passo (o segmento de reta P1 P3 n˜o ´ mostrado porque
o a e
n˜o ´ utilizado para determinar os ˆngulos de rota¸˜o. Ambos os segmento s˜o rotacionados por Rx (φ).)
a e a ca a
O ˆngulo de rota¸˜o ´ φ, e
a ca e
z2
cos φ =
D2
y
sin φ = 2 (5.68)
D2
66

68. onde D2 = |P1 P2 | ´ o comprimento do segmento de reta P1 P2 . Como as transla¸˜es e rota¸˜es preservam
e co co
o comprimento, o comprimento de P1 P2 ´ o mesmo de P1 P2 , dessa forma
e
D2 = |P1 P2 | = |P1 P2 | = (x2 − x1 )2 + (y2 − y1 )2 + (z2 − z1 )2 (5.69)
O resultado da rota¸˜o no terceiro passo ´:
ca e
0
 
 0 
P2 = Rx (φ) · P2 = Rx (φ) · Ry (θ − 90o ) · P2 = Rx (φ) · Ry (θ − 90o ) · T · P2 =  (5.70)
|P1 P2 |

1
Dessa forma, agora P1 P2 agora est´ sobre (coincidindo) o eixo z positivo.
a
Quarto Passo: Rotacionar em Rela¸˜o ao eixo Z
ca
Figura 5.19: Rota¸˜o em rela¸˜o ao eixo z.
ca ca
A figura 5.19 mostra P1 P2 e P1 P3 ap´s o terceiro passo, com P2 sobre o eixo z e P3 em
o
x3
 
y 
P3 =  3  = Rx (φ) · Ry (θ − 90o ) · T (−x1 , −y1 , −z1 ) · P3 (5.71)
z3
1
A rota¸˜o ´ dada pelo ˆngulo positivo α, e
ca e a
y3
cos α =
D3
x
sin α = 3
D3
D3 = x3 2 + y3 2 (5.72)
P1 P3 ´ trazido para o plano yz.
e
Dessa forma, ap´s o quarto passo o resultado ´ alcan¸ado como visto na Figura 5.16(b).
o e c
A matriz de composi¸˜o M ´ a transforma¸˜o necess´ria ` composi¸˜o solicitada na Figura 5.16.
ca e ca a a ca
M = Rx (α) · Rx (φ) · Ry (θ − 90o ) · T (−x1 , −y1 , −z1 ) = R · T (5.73)
Exerc´ıcio: aplique a matriz de composi¸˜o a cada um dos pontos P1 , P2 e P3 para verificar que P1
ca
´ transformado para a origem, P2 est´ sobre o eixo z positivo e P3 no plano yz positivo.
e a
67

69. Utilizando as propriedades de matrizes ortogonais (ver Equa¸˜es 5.61, 5.62 e a observa¸˜o da se¸˜o
co ca ca
5.8), podemos encontrar uma segunda forma de encontrar a matriz de transforma¸˜es. Relembremos que
co
os vetores unit´rios (de comprimento igual a 1) de R rotacionam em rela¸˜o aos eixos principais.
a ca
Assim,
 
r1x r2x r3x
R =  r1y r2y r3y  (5.74)
r1z r2z r3z
Colocando Rz como o vetor unit´rio ao longo de P1 P2 que ir´ rotacionar em dire¸˜o ao eixo z positivo,
a a ca
T P1 P2
Rz = [ r1z r2z r3z ] = (5.75)
|P1 P2 |
O vetor unit´rio Rx ´ perpendicular ao plano de P1 , P2 e P3 e ir´ rotacionar em dire¸˜o ao eixo
a e a ca
x positivo, dessa forma Rx deveria ser o produto vetorial de dois vetores do plano (relembre-se das
propriedades de Produto Vetorial vistos em Geometria Anal´
ıtica !):
T P1 P3 × P1 P2
Rx = [ r1x r2x r3x ] = (5.76)
|P1 P3 × P1 P2 |
e finalmente,
T
Ry = [ r1x r2y r3z ] = Rz × Rx (5.77)
ir´ rotacionar em dire¸˜o ao eixo y positivo. A matriz de composi¸˜o ´ dada por
a ca ca e
r1x r2x r3x 0
 
 r1y r2y r3y 0
 · T (−x1 , −y1 , −z1 ) = R · T (5.78)
r1z r2z r3z 0

0 0 0 1
Figura 5.20: Os vetores unit´rios Rx , Ry e Rz , os quais s˜o transformados nos eixos principais.
a a
e R e T s˜o como em 5.78. A Figura 5.20 mostra os vetores individuais Rx , Ry e Rz .
a
68

70. Cap´
ıtulo 6
Observa¸˜o de Cenas 3D
ca
6.1 Pipeline de observa¸˜o (“viewing pipeline”)
ca
Ap´s a cria¸˜o de cenas e objetos tridimensionais o pr´ximo passo ´ efetuar a sua apresenta¸˜o. Ao
o ca o e ca
gerar imagens de cenas 3D em computa¸˜o gr´fica, fazemos uma analogia com uma cˆmera fotogr´fica:
ca a a a
imaginamos um observador que, posicionado em um ponto de observa¸˜o, vˆ a cena atrav´s das lentes de
ca e e
uma cˆmera virtual que pode ser posicionada de forma a obter a imagem desejada da cena (o “fot´grafo”
a o
pode definir a posi¸˜o da cˆmera, sua orienta¸˜o e ponto focal). A fotografia que se obt´m com uma
ca a ca e
cˆmera real ´ uma proje¸˜o da cena em um plano de imagem 2D (o filme na cˆmera). Da mesma forma
a e ca a
que no mundo real, a imagem que se obt´m da cena sint´tica depende de v´rios fatores que determinam
e e a
como esta ´ projetada em um plano para formar a imagem 2D exibida (por exemplo) no monitor. Estes
e
parˆmetros incluem a posi¸˜o da cˆmera, sua orienta¸˜o e ponto focal, o tipo de proje¸˜o efetuada
a ca a ca ca
e a posi¸˜o dos “planos de recorte” (clipping planes).
ca
A posi¸˜o e o ponto focal da cˆmera definem, respectivamente, aonde a cˆmera est´ e para onde
ca a a a
ela est´ apontando. O vetor que vai da posi¸˜o da cˆmera ao ponto focal ´ denominado dire¸˜o de
a ca a e ca
proje¸˜o. O plano de imagem, que ´ o plano no qual a cena ser´ projetada, est´ posicionado no ponto
ca e a a
focal e, tipicamente, ´ perpendicular ao vetor dire¸˜o de proje¸˜o (Figura 6.1). A orienta¸˜o da cˆmera
e ca ca ca a
´ controlada pela sua posi¸˜o, seu ponto focal e por um outro vetor denominado view up. Estes trˆs
e ca e
parˆmetros definem completamente a cˆmera.
a a
Figura 6.1: Atributos da cˆmera [Schr¨eder, 1998].
a o
O m´todo de proje¸˜o controla como os atores da cena s˜o mapeados no plano de imagem: na proje¸˜o
e ca a ca
ortogr´fica, ou proje¸˜o paralela, o processo de mapeamento ´ paralelo: assume-se que todos os raios de
a ca e
luz que atingem a cˆmera s˜o paralelos ao vetor de proje¸˜o. Na proje¸˜o perspectiva, todos os raios
a a ca ca
convergem para um ponto comum, denominado ponto de observa¸˜o, ou centro da proje¸˜o. Nesse caso,
ca ca
deve-se determinar o ˆngulo de vis˜o da cˆmera.
a a a
Os planos de recorte anterior e posterior interceptam o vetor de proje¸˜o e s˜o, geralmente, per-
ca a
pendiculares a ele. Os planos de recorte s˜o usados para eliminar atores que est˜o muito pr´ximos ou
a a o
muito distantes da cˆmera, de forma que apenas os atores que est˜o na ´rea englobada pelos planos
a a a
de recorte s˜o potencialmente vis´
a ıveis. Em geral, os planos de recorte s˜o perpendiculares ` dire¸˜o
a a ca
69

71. de proje¸˜o. Suas posi¸˜es podem ser especificadas usando o chamado intervalo de recorte (“clipping
ca co
range”) da cˆmera: a localiza¸˜o dos planos ´ dada a partir da posi¸˜o da cˆmera, ao longo da dire¸˜o
a ca e ca a ca
de proje¸˜o. A posi¸˜o do plano anterior d´ o valor m´
ca ca a ınimo do intervalo, e a posi¸˜o do plano posterior
ca
d´ o valor m´ximo.
a a
A cˆmera pode ser manipulada diretamente atrav´s dos parˆmetros acima descritos, mas existem
a e a
algumas opera¸˜es comuns que facilitam a tarefa de quem gera a imagem, como ilustradas nas figuras
co
6.2 e 6.3:
• Azimuth - rotaciona a posi¸˜o da cˆmera ao redor do seu vetor view up, com centro no ponto focal
ca a
• Elevation - rotaciona a posi¸˜o da cˆmera ao redor do vetor dado pelo produto vetorial entre o
ca a
vetor view up e o vetor dire¸˜o de proje¸˜o, com centro no ponto focal.
ca ca
• Roll (Twist) - rotaciona o vetor view up em torno do vetor normal ao plano de proje¸˜o.
ca
• Yaw - rotaciona o ponto focal da cˆmera em torno do vetor view up, com centro na posi¸˜o da
a ca
cˆmera.
a
• Pitch - rotaciona o ponto focal ao redor do vetor dado pelo produto vetorial entre o vetor view up
e o vetor dire¸˜o de proje¸˜o, com centro na posi¸˜o da cˆmera.
ca ca ca a
• Dolly - (in, out) move a posi¸˜o da cˆmera ao longo da dire¸˜o de proje¸˜o (mais pr´ximo ou mais
ca a ca ca o
distante do ponto focal).
• Zoom - altera o ˆngulo de vis˜o da cˆmera, de modo que uma regi˜o maior ou menor da cena fique
a a a a
na regi˜o que ´ potencialmente vis´
a e ıvel.
Figura 6.2: Movimentos de cˆmera [Schr¨eder, 1998].
a o
Em resumo, gerar uma vista de um objeto em trˆs dimens˜es ´ similar a fotografar o objeto. Podemos
e o e
caminhar na cena e fotografar de qualquer ˆngulo, de v´rias distˆncias e com diferentes orienta¸˜es da
a a a co
cˆmera. A regi˜o da cena que aparece no visor da m´quina ´ o que vai ser projetado na superf´ do
a a a e ıcie
filme. O tipo e o tamanho da lente da cˆmera determinam quais partes da cena aparecem na foto final.
a
Estas id´ias est˜o incorporadas nas APIs gr´ficas 3D, de forma que vistas de uma cena podem ser geradas
e a a
a partir da defini¸˜o de parˆmetros como posi¸˜o espacial, orienta¸˜o e ˆngulo de abertura da “cˆmera
ca a ca ca a a
virtual”.
6.2 Coordenadas de Observa¸˜o
ca
6.2.1 Especifica¸˜o do sistema de coordenadas de observa¸˜o
ca ca
Escolhemos uma “vista” espec´
ıfica para uma cena estabelecemos primeiramente um sistema de coordena-
das de observa¸˜o (Viewing Coordinate System - VCS, ou View reference Coordinate System). Um plano
ca
70

72. Figura 6.3: Movimentos de cˆmera [Schr¨eder, 1998].
a o
de observa¸˜o, ou plano de proje¸˜o, ´ definido, que ´ perpendicular ao eixo z do sistema de coordenadas
ca ca e e
de visualiza¸˜o VCS (esse plano faz o papel do plano do filme na cˆmera virtual). Em seguida, ´ preciso
ca a e
transformar a descri¸˜o da cena dada no sistema de coordenadas do mundo (WC - World Coordinates)
ca
para uma descri¸˜o no sistema de coordenadas de observa¸˜o VCS.
ca ca
Mas, como determinamos o VCS? Inicialmente, estabelecemos a origem do sistema. Para isso, usamos
um ponto inicialmente definido no WC, o View Reference Point - VRP. Podemos pensar nesse ponto como
sendo a posi¸˜o da cˆmera. Em seguida, selecionamos a dire¸˜o positiva para o eixo z do VCS (vamos
ca a ca
denotar esse eixo por zv ), bem como a orienta¸˜o do plano de observa¸˜o, especificando o vetor normal
ca ca
ao plano de observa¸˜o, N . Finalmente, definimos a dire¸˜o do eixo y do VCS (yv ) especificando-se um
ca ca
vetor V (View Up). Obviamente, V deve ser perpendicular a N . Pode ser dif´ para o programador
ıcil
determinar V exatamente de forma a satisfazer essa condi¸˜o. Tipicamente, as transforma¸˜es de ob-
ca co
serva¸˜o implementadas nos pacotes gr´ficos ajustam V projetando-o em um plano que ´ perpendicular
ca a e
ao vetor N : dessa forma, o programador pode escolher qualquer dire¸˜o conveniente para o vetor V ,
ca
desde que n˜o seja paralela ` N . A partir dos vetores N e V , o pacote gr´fico pode computar um terceiro
a a a
vetor U , perpendicular a ambos, que define a dire¸˜o para o eixo xv do VCS (veja Figuras 6.4 e 6.5).
ca
Figura 6.4: Um VCS baseado na regra da m˜o direita com xv , yv e zv .relativos ao sistema de coordenadas
a
do mundo [Hearn and Baker, 1994].
6.2.2 Transforma¸˜o do sistema de coordenadas do mundo para o sistema de
ca
coordenadas de observa¸˜o
ca
Antes que as descri¸˜es do objeto (em WC) possam ser projetadas no plano de observa¸˜o, elas preci-
co ca
sam ser transformadas para as coordenadas do VCS. A convers˜o das coordenadas de WC para VCS ´
a e
71

73. Figura 6.5: Orienta¸˜es do plano de observa¸˜o conforme o vetor normal. O vetor (1, 0, 0) d´ a orienta¸˜o
co ca a ca
em (a) e (1, 0, 1), a orienta¸˜o em (b) [Hearn and Baker, 1994].
ca
equivalente a uma transforma¸˜o que superp˜e o VCS ao WC, usando as transforma¸˜es geom´tricas j´
ca o co e a
vistas. A seq¨ˆncia de transforma¸˜es ´ dada por:
ue co e
1. translada o VRP para a origem do WC .
2. Aplica rota¸˜es para alinhar os eixos do VCS (xv , yv , zv ) com os eixos do WC (xw , yw , zw ), respec-
co
tivamente.
Se as coordenadas do ponto VRP em WC s˜o dadas por (x0 , y0 , z0 ), a matriz de transla¸˜o ´ dada por
a ca e
T (−x0 , −y0 , −z0 ). A seq¨ˆncia de rota¸˜es pode exigir at´ trˆs rota¸˜es em torno dos eixos coordenados,
ue co e e co
dependo da dire¸˜o escolhida para N . Em geral, se N n˜o est´ alinhado com qualquer um dos eixos, a
ca a a
superposi¸˜o de ambos os sistemas vai exigir uma seq¨ˆncia Rz · Ry · Rx . Isto ´, primeiro rotacionamos
ca ue e
em torno do eixo xw para trazer o eixo zv para o plano xw zw . Em seguida, rotacionamos em torno do
eixo yw para alinhar os eixos zw e zv . A rota¸˜o final em torno do eixo zw ´ para alinhar os eixos yw e
ca e
yv . A matriz de transforma¸˜o composta ´ ent˜o aplicada a todas as descri¸˜es de objetos no WC para
ca e a co
transform´-las para VCS.
a
Uma forma alternativa de gerar a matriz que descreve as transforma¸˜es de rota¸˜o necess´rias ´
co ca a e
calcular os vetores unit´rios u, v e n do sistema de coordenadas de observa¸˜o, e formar a matriz
a ca
de composi¸˜o diretamente, uma vez que esses vetores s˜o ortogonais entre si e definem uma matriz
ca a
ortogonal. Dados os vetores N e V , os vetores unit´rios podem ser calculados da seguinte forma:
a
N
n= = (n1 , n2 , n3 ) (6.1)
|N |
V ×N
u= = (u1 , u2 , u3 ) (6.2)
|V × N |
v = n × u = (v1 , v2 , v3 ) (6.3)
Este m´todo tamb´m ajusta automaticamente a dire¸˜o de V de forma que v seja perpendicular a n.
e e ca
A matriz de rota¸˜o composta para a transforma¸˜o de visualiza¸˜o ´ ent˜o dada por:
ca ca ca e a
u1 u2 u3 0
 
 v1 v2 v3 0
R= (6.4)
n1 n2 n3 0

0 0 0 1
A matriz de transforma¸˜o completa a ser aplicada aos objetos da cena para transferi-los para o
ca
sistema de coordenadas de observa¸˜o ´ dada por:
ca e
u1 u2 u3 −x0
 
 v1 v2 v3 −y0 
Mwc,vc =R·T = (6.5)
n1 n2 n3 −z0

0 0 0 1
72

74. 6.3 Proje¸˜es
co
Tendo os objetos descritos no sistema de coordenadas de observa¸˜o, pode-se projetar os objetos tridi-
ca
mensional no plano de observa¸˜o. No processo de gera¸˜o da imagem de uma cena deparamos com o
ca ca
problema de apresentar uma entidade tridimensional num meio bidimensional (2D), que ´ a tela do moni-
e
tor de v´ıdeo. Esse processo, denominado de Proje¸˜o, tem sido tratado exaustivamente por desenhistas,
ca
artistas e arquitetos que buscaram t´cnicas e artif´
e ıcios para sistematiz´-lo e solucion´-lo. A figura 6.6
a a
apresenta uma taxonomia dos m´todos de proje¸˜o.
e ca
Figura 6.6: Taxomia de proje¸˜es [Plastock and Kalley, 1999].
co
6.3.1 Proje¸˜o Perspectiva
ca
As t´cnicas utilizadas em proje¸˜o perspectiva s˜o derivadas daquelas utilizadas pelos artistas e dese-
e ca a
nhistas profissionais. Pode-se dizer que o olho do observador coloca-se no centro de proje¸˜o, e o plano
ca
que deve conter o objeto ou cena projetada transforma-se no plano de proje¸˜o. Dois segmentos de reta
ca
que saem do centro de proje¸˜o e atingem o objeto projetado no plano de proje¸˜o, s˜o chamadas de
ca ca a
projetantes (veja a Figura 6.7)
Figura 6.7: Linha AB e sua proje¸˜o A’B’: (a) perspectiva; (b) ortogonal.
ca
Os desenhos em perspectiva s˜o caracterizados pelo encurtamento perspectivo e pelos pontos de fuga.
a
O encurtamento perspectivo, ´ a ilus˜o de que os objetos e comprimentos s˜o cada vez menores ` medida
e a a a
que sua distˆncia ao centro de proje¸˜o aumenta. Tem-se tamb´m a ilus˜o de que conjuntos de linhas
a ca e a
paralelas que n˜o s˜o paralelas ao plano de proje¸˜o, convergem para um ponto de fuga. Denominam-se
a a ca
73

75. pontos de fuga principais, quando d´-se a aparˆncia de haver uma intersec¸˜o entre um conjunto de
a e ca
retas pararelas com um dos eixos principais Ox , Oy ou Oz . O n´mero de pontos de fuga principais ´
u e
determinado pelo n´mero de eixos principais intersectados pelo plano de proje¸˜o. Por exemplo: se o
u ca
plano de proje¸˜o intercepta apenas os eixo z (ent˜o ´ perpendicular ao eixo z), somente o eixo z possui
ca a e
um ponto de fuga principal, pois linhas paralelas aos eixos x e y, s˜o tamb´m paralelas ao plano de
a e
proje¸˜o, e dessa forma n˜o ocorre a ilus˜o de convergˆncia.
ca a a e
Proje¸˜es Perspectivas s˜o categorizadas pelo seu n´mero de pontos de fuga principais, ou seja o
co a u
n´mero de eixos que o plano de proje¸˜o intercepta. A Figura 6.8 mostra 2 proje¸˜es perspectivas (com
u ca co
um ponto de fuga) distintas de um cubo. Est´ claro que possui apenas um ponto de fuga? Somente as
a
linhas paralelas ao eixo z convergem, e as linhas paralelas aos eixos x e y continuam paralelas!
Figura 6.8: Proje¸˜es de um cubo (com 1 ponto de fuga) sobre um plano cortando o eixo Z, apresentando
co
o ponto de fuga.
Proje¸˜es perspectivas com 2 pontos de fuga (quando 2 eixos principais s˜o interceptados pelo plano
co a
de proje¸˜o) s˜o mais comumente usadas em arquitetura, engenharia, desenho publicit´rio e projeto
ca a a
industrial (ver Figura 6.9). J´ as proje¸˜es perspectivas com 3 pontos de fuga s˜o bem menos utilizadas,
a co a
pois adicionam muito pouco em termos de realismo comparativamente `s proje¸˜es com 2 pontos de fuga,
a co
e o custo de implementa¸˜o ´ bem maior (veja Figura 6.10).
ca e
Figura 6.9: Proje¸˜es perspectivas com 2 pontos de fuga ( o plano de proje¸˜o intercepta 2 eixos (x e z)).
co ca
Anomalias da Perspectiva
A proje¸˜o perspectiva introduz certas anomalias que aumentam o realismo em termos de profundidade,
ca
mas tamb´m alteram as medidas e formas reais do objetos.
e
1. Encurtamente perspectivo: Quanto mais distante um objeto est´ do centro de proje¸˜o, menor
a ca
parece ser (o tamanho de sua proje¸˜o torna-se menor, como mostra a figura 6.11.
ca
2. pontos de Fuga: As proje¸˜es de retas n˜o paralelas ao plano de proje¸˜o, provocam a ilus˜o de
co a ca a
que se interceptam num ponto do horizonte.
3. Confus˜o Visual: Os objetos situados atr´s do centro de proje¸˜o s˜o projetados no plano de
a a ca a
proje¸˜o de cima para baixo e de tr´s para a frente (ver Figura 6.12)
ca a
4. Distor¸˜o Topol´gica: Consideremos o plano que cont´m o centro de proje¸˜o e que ´ paralelo do
ca o e ca e
plano de proje¸˜o. Os pontos deste plano s˜o projetados no infinito pela transforma¸˜o perspectiva.
ca a ca
74

76. Figura 6.10: Proje¸˜es perspectivas com 3 pontos de fuga ( o plano de proje¸˜o intercepta os 3 eixos).
co ca
Em particular, um segmento de reta que une um ponto situado ` frente do observador a um ponto
a
situado atr´s dele e efetivamente projetado segundo uma linha quebrada de comprimento infinito.
a
Figura 6.11: A esfera B ´ bem maior que a esfera A, por´m ambas aparecem com o mesmo tamanho
e e
quando projetadas no plano de vis˜o.
a
Desenvolvimento Matem´tico para Proje¸˜es Perspectivas
a co
Para obter uma proje¸˜o perspectiva de um objeto 3D, s˜o transformados os pontos ao longo dos pro-
ca a
jetores que se encontram no centro de proje¸˜o. Suponha que o centro de proje¸˜o est´ posicionado
ca ca a
em zprp, um ponto no eixo zv, e que o plano de proje¸˜o, normal ao eixo z, est´ posicionado em zvp,
ca a
como mostra a Figura 6.13. Precisamos determinar as coordenadas (xp , yp , zp ), que s˜o as coordenadas
a
do ponto P = (x, y, z) projetado no plano de proje¸˜o. Podemos escrever as equa¸˜es que descrevem as
ca co
coordenadas (x , y , z ) de qualquer ponto ao longo da linha de proje¸˜o perspectiva como:
ca
x = x − xu
y = y − yu
z = z − (z − zprp )u (6.6)
O parˆmetro u assume valores no intervalo [0, 1] quando u = 0, estamos em P = (x, y, z), e quando
a
u = 1 temos exatamente o centro de proje¸˜o (0, 0, zprp ). As proje¸˜es perspectiva e paralela tamb´m
ca co e
podem, assim como as transforma¸˜es geom´tricas b´sica, ser definidas atrav´s de matrizes 4x4, o que ´
co e a e e
interessante para a composi¸˜o de transforma¸˜es juntamente com a proje¸˜o. No plano de observa¸˜o,
ca co ca ca
sabemos que z = zvp , e podemos resolver a equa¸˜o de z’ para obter o valor do parˆmetro u nessa posi¸˜o
ca a ca
ao longo da linha de proje¸˜o:
ca
Zvp − z
u= (6.7)
Zprp − z
75

77. Figura 6.12: Confus˜o visual da perpectiva (objeto atr´s do centro de proje¸˜o).
a a ca
Figura 6.13: Proje¸˜o em perspectiva de um ponto P=(x, y, z) na posi¸˜o (xp, yp, zp) sobre o plano de
ca ca
proje¸˜o [Hearn and Baker, 1994].
ca
Substituindo esse valor de u nas equa¸˜es de z e y , obtemos as equa¸˜es de transforma¸˜o perspectiva:
co co ca
Zvp − z dp
xp = x =x
Zprp − z Zprp − z
Zvp − z dp
yp = y =y (6.8)
Zprp − z Zprp − z
Usando coordenadas homogˆneas pode-se escrever a transforma¸˜o na forma matricial:
e ca
 1 0 0 0
  
xh x

 yh   0 1 0 0  y
  =  0 0 − zvp zprp ·  (6.9)
zh  dp −zvp dp  z
z rp
h 0 0 − d1
p
− pp
d
1
Nesta representa¸˜o o fator homogˆneo ´
ca e e
zprp − z
h= (6.10)
dp
E as coordenadas do ponto projetado no plano de observa¸˜o s˜o obtidas a partir das coordenadas
ca a
homogˆneas dividindo-se por h:
e
xh
xp =
h
yh
yp = (6.11)
h
Observa-se que o valor original da coordenada z precisa ser mantido nas coordenadas de proje¸˜o
ca
para uso por algoritmos de remo¸˜o de linhas ocultas. Em geral, o centro da proje¸˜o n˜o precisa ser
ca ca a
76

78. posicionado ao longo do eixo zv , e as equa¸˜es acima podem ser generalizadas para considerar o centro
co
em um ponto qualquer. Existem v´rios casos especiais a serem considerados para as equa¸˜es acima.
a co
Por exemplo, se o plano de proje¸˜o coincide com o plano uv, i.e., zvp = 0, ent˜o dp = zprp . Em alguns
ca a
pacotes gr´ficos ´ assumido que o centro de proje¸˜o coincide com a origem do sistema de coordenadas
a e ca
de observa¸˜o, i.e., nesse caso zprp = 0.
ca
6.3.2 Desenvolvimento Matem´tico para Proje¸˜es Paralelas
a co
Podemos especificar uma proje¸˜o paralela com um vetor de proje¸˜o que define a dire¸˜o dos projeto-
ca ca ca
res. Quando a dire¸˜o proje¸˜o ´ perpendicular ao plano de proje¸˜o tem-se uma proje¸˜o ortogr´fica,
ca ca e ca ca a
caso contr´rio tem-se uma proje¸˜o obl´
a ca ıqua. Proje¸˜es ortogr´ficas s˜o muito comuns em engenharia e
co a a
arquitetura para gerar vistas frontais, laterais e traseiras de objetos. A deriva¸˜o das equa¸˜es de trans-
ca co
forma¸˜o para uma proje¸˜o paralela ortogr´fica ´ imediata. Se o plano de observa¸˜o est´ posicionado
ca ca a e ca a
em zvp ao longo do eixo zv , ent˜o a descri¸˜o de qualquer ponto P = (x, y, z) em coordenadas do sistema
a ca
de observa¸˜o ´ transformada para as coordenadas de proje¸˜o (veja Figura 6.14):
ca e ca
Figura 6.14: Proje¸˜o ortogonal de um ponto no plano de proje¸˜o [Hearn and Baker, 1994].
ca ca
A matriz de transforma¸˜o para coordenadas homogˆneas ´ dada por:
ca e e
1 0 0 0
 
0 1 0 0
Mortograf = (6.12)
0 0 0 0

0 0 0 1
77

79. Cap´
ıtulo 7
Recorte de Primitivas 2D
J´ vimos que um “pacote gr´fico” atua como intermedi´rio entre o aplicativo (e o seu modelo/estrutura de
a a a
dados interna) e o hardware de visualiza¸˜o. Sua fun¸˜o ´ aproximar primitivas matem´ticas (“ideais”),
ca ca e a
descritas em termos de v´rtices num sistema de coordenadas cartesianas, por conjuntos de pixels com a
e
cor ou n´ de cinza apropriado. Estes pixels s˜o armazenados num bitmap na mem´ria da CPU, ou num
ıvel a o
frame buffer (mem´ria de imagem no controlador do dispositivo. At´ o momento estudamos, de maneira
o e
n˜o extensiva, alguns algoritmos b´sicos para convers˜o matricial utilizados por pacotes gr´ficos. Vamos
a a a a
estudar agora alguns algoritmos para clipping [recorte] de primitivas. (O “recorte” ´ necess´rio para que
e a
a imagem “apare¸a” dentro do retˆngulo de visualiza¸˜o definido para ela.
c a ca
Existem v´rias abordagens para o processo de clipping. Uma t´cnica ´bvia ´ recortar a primi-
a e o e
tiva antes da convers˜o matricial, calculando analiticamente suas intersec¸˜es com o retˆngulo de re-
a co a
corte/visualiza¸˜o [clip rectangle]. Estes pontos de intersec¸˜o s˜o ent˜o usados para definir os novos
ca ca a a
v´rtices para a vers˜o recortada da primitiva. A vantagem, evidente, ´ que o processo de convers˜o
e a e a
matricial precisa tratar apenas da vers˜o recortada da primitiva, cuja ´rea pode ser muito menor que a
a a
original. Esta ´ a t´cnica mais freq¨entemente utilizada para recortar segmentos de reta, retˆngulos e
e e u a
pol´ıgonos, e os algoritmos que vamos estudar s˜o baseados nesta estrat´gia.
a e
Outra estrat´gia seria converter todo o pol´
e ıgono, mas tra¸ar apenas os pixels vis´
c ıveis no retˆngulo de
a
visualiza¸˜o [scissoring]. lsto pode ser feito checando as coordenadas de cada pixel a ser escrito contra
ca
os limites do retˆngulo. Na pr´tica, existem maneiras de acelerar o processo que evitam o teste de cada
a a
pixel individualmente. Se o teste dos limites puder ser feito rapidamente [por hardware especializado,
por exemplo], esta abordagem pode ser mais eficiente que a anterior, e tem a vantagem de ser extens´ ıvel
a regi˜es de recorte arbitr´rias.
o a
7.1 Recorte de segmentos de reta
Figura 7.1: Exemplos de recorte de segmentos de reta.
Vamos estudar especificamente o processo de recorte de segmentos de reta contra retˆngulos. Segmen-
a
tos que interceptam uma regi˜o de recorte retangular, depois de recortados, s˜o sempre transformados
a a
num unico segmento. Segmentos que est˜o sobre a fronteira do retˆngulo de recorte s˜o considerados
´ a a a
como dentro dele, e portanto devem ser mostrados (Figura 7.1).
78

80. 7.1.1 Recorte de Pontos Extremos
Antes de discutir o problema do recorte de segmentos de reta, vamos considerar o problema mais simples
de recortar pontos extremos. Se a fronteira do retˆngulo de recorte tem coordenada x no intervalo xmin
a
e xmax , e coordenada y no intervalo ymin e ymax , ent˜o 4 desigualdades precisam ser satisfeitas para que
a
um ponto (x, y) esteja dentro do retˆngulo de recorte:
a
xmin ≤ x ≤ xmax
ymin ≤ y ≤ ymax (7.1)
7.1.2 Algoritmo de Cohen-Sutherland para Recorte de Segmentos de Reta
Para recortar um segmento de reta, precisamos considerar apenas os seus pontos extremos, e n˜o os a
infinitos pontos no interior. Se ambas as extremidades est˜o dentro do retˆngulo de visualiza¸˜o (AB na
a a ca
Figura 7.1), toda a linha est´ dentro do retˆngulo e pode ser tra¸ada (neste caso diz-se que a reta foi
a a c
trivialmente aceita). Se apenas uma das extremidades est´ dentro (CD na Figura 7.1), a linha intercepta
a
o retˆngulo de visualiza¸˜o, e o ponto de intersec¸˜o precisa ser calculado. Se ambas as extremidades
a ca ca
est˜o fora, a linha pode ou n˜o interceptar o retˆngulo, e precisamos verificar se as intersec¸˜es existem
a a a co
e onde est˜o.a
Uma estrat´gia de for¸a bruta seria checar a linha contra cada aresta do retˆngulo de visualiza¸˜o, para
e c a ca
localizar um eventual ponto de intersec¸˜o. Se existe um, a linha corta o retˆngulo, e est´ parcialmente
ca a a
dentro dele. Para cada linha e cada aresta do retˆngulo, tomamos as duas retas (matematicamente
a
infinitas) que as cont´m, e calculamos a intersec¸˜o entre elas. A seguir, testamos se este ponto ´ interior
e ca e
- ou seja, se est´ dentro do retˆngulo de visualiza¸˜o e da linha. Se este ´ o caso, existe uma intersec¸˜o
a a ca e ca
com o retˆngulo de visualiza¸˜o. Na Figura 7.1, os pontos de intersec¸˜o G e H s˜o interiores, mas I
a ca ca a
e J n˜o s˜o.
a a
Nesta abordagem, precisamos resolver duas equa¸˜es simultˆneas usando multiplica¸˜o e divis˜o para
co a ca a
cada par < aresta, linha >. Entretanto, este ´ um esquema bastante ineficiente, que envolve quantidade
e
consider´vel de c´lculos e testes, e portanto deve ser descartado.
a a
O algoritmo de Cohen-Sutherland ´ mais eficiente, e executa testes iniciais na linha para determinar
e
se c´lculos de intersec¸˜o podem ser evitados. Primeiramente, verifica pares de pontos extremos. Se a
a ca
linha n˜o pode ser trivialmente aceita, s˜o feitas verifica¸˜es por regi˜es. Por exemplo, duas compara¸˜es
a a co o co
simples em x mostram que ambos os pontos extremos da linha EF na Figura 7.1 tˆm coordenada x menor
e
que xmin, e portanto est˜o na regi˜o a esquerda do retˆngulo de visualiza¸˜o (ou seja, fora do semi-plano
a a a ca
definido pela aresta esquerda). A consequˆncia ´ que o segmento EF pode ser trivialmente rejeitado, e
e e
n˜o precisa ser recortado ou tra¸ado. Da mesma forma, podemos rejeitar trivialmente linhas com ambos
a c
os extremos em regi˜es a direita de xmax , abaixo de ymin e acima de ymax . Se o segmento n˜o pode ser
o a
trivialmente aceito ou rejeitado, ele ´ subdividido em dois segmentos por uma aresta de recorte, um dos
e
quais pode ser trivialmente rejeitado. Dessa forma, um segmento ´ recortado interativamente testando-se
e
aceita¸˜o ou rejei¸˜o trivial, sendo subdividido se nenhum dos dois testes for bem-sucedido, at´ que o
ca ca e
segmento remanescente esteja totalmente contido no retˆngulo ou totalmente fora dele.
a
Para executar os testes de aceita¸˜o ou rejei¸˜o trivial, as arestas do retˆngulo de visualiza¸˜o s˜o
ca ca a ca a
estendidas de forma a dividir o plano do retˆngulo de visualiza¸˜o em 9 regi˜es [Figura 7.2]. A cada
a ca o
regi˜o ´ atribu´ um c´digo de 4 bits, determinado pela posi¸˜o da regi˜o com rela¸˜o aos semi-planos
a e ıdo o ca a ca
externos `s arestas do retˆngulo de recorte. Uma maneira eficiente de calcular os c´digos resulta da
a a o
observa¸˜o de que o bit 1 ´ igual ao bit de sinal de (ymax − y); o 2 ´ o bit de sinal de (y − ymin ); o 3 ´ o
ca e e e
bit de sinal de (xmax − x), e o 4 e o de (x − xmin ).
• 1◦ bit: semiplano acima da aresta superior y > ymax
• 2◦ bit: semiplano abaixo da aresta inferior y < ymin
• 3◦ bit: semiplano a direita da aresta direita x > xmax
• 4◦ bit: semiplano a esquerda da aresta esquerda x < xmin
A cada extremidade do segmento de reta ´ atribu´ o c´digo da regi˜o a qual ela pertence. Esses
e ıdo o a
c´digos s˜o usados para determinar se o segmento est´ completamente dentro do retˆngulo de visualiza¸˜o
o a a a ca
ou em um semiplano externo a uma aresta. Se os 4 bits dos c´digos das extremidades s˜o iguais a zero,
o a
ent˜o a linha est´ completamente dentro do retˆngulo. Se ambas as extremidades estiverem no semi plano
a a a
externo a uma aresta em particular, como para EF na Figura 7.1, os c´digos de ambas as extremidades
o
tem o bit correspondente `quela aresta igual a 1. Para EF, os c´digos s˜o 0001 e 1001, respectivamente,
a o a
79

81. Figura 7.2: C´digos das regi˜es.
o o
o que mostra com o 4◦ bit que o segmento est´ no semiplano externo ` aresta esquerda. Portanto, se
a a
um and bit a bit dos c´digos das extremidades for diferente de zero, o segmento pode ser trivialmente
o
rejeitado.
Se a linha n˜o puder ser trivialmente aceita ou rejeitada, devemos subdividi-la em dois segmentos de
a
forma que um deles possa ser rejeitado. A subdivis˜o ´ feita usando uma aresta que seja interceptada pela
a e
linha para subdividi-la em dois segmentos: a se¸˜o que fica no semiplano externo ` aresta ´ descartada. 0
ca a e
teste de quais arestas interceptam a linha segue a mesma ordem dos bits nos c´digos: de cima-para-baixo,
o
da direita-para-a-esquerda. Uma propriedade chave dos c´digos ´ que os bits iguais a um correspondem
o e
a arestas interceptadas: se uma extremidade est´ no semiplano externo a uma aresta, e o segmento falha
a
nos testes de rejei¸˜o trivial, ent˜o a outra extremidade deve estar no semiplano interno `quela aresta,
ca a a
que ´ portanto interceptada pelo segmento. Assim, o algoritmo sempre escolhe um ponto que esteja fora,
e
e usa os bits do c´digo iguais a um) para determinar uma aresta de recorte. A aresta escolhida ´ a
o e
primeira encontrada na ordem pr´-definida, ou seja, a correspondente ao primeiro bit igual a 1 no c´digo.
e o
0 algoritmo funciona da seguinte maneira: Calcula primeiramente os c´digos de ambas as extremi-
o
dades, e checa aceita¸˜o ou rejei¸˜o trivial. Se nenhum dos testes for bem-sucedido, tomamos uma
ca ca
extremidade externa (pelo menos uma delas ´ externa), e testamos seu c´digo para obter uma aresta que
e o
seja interceptada e determinar o ponto de intersec¸˜o. Podemos ent˜o descartar o segmento que vai do
ca a
extremo externo ao ponto de intersec¸˜o, substituindo o ponto externo pela intersec¸˜o. 0 novo c´digo
ca ca o
para o segmento correspondente ´ calculado, preparando os dados para a pr´xima itera¸˜o.
e o ca
Considere por exemplo o segmento AD na Figura 7.4. 0 c´digo do ponto A ´ 0000, e o do ponto D
o e
´ 1001 . O segmento n˜o pode ser trivialmente aceito ou rejeitado. 0 algoritmo escolhe D como o ponto
e a
externo, e o seu c´digo mostra que a linha cruza as arestas superior e esquerda. De acordo com a ordem
o
de teste, usamos primeiro a aresta superior para recortar AD, gerando B. O c´digo de B ´ 0000 e na
o e
pr´xima intera¸˜o o segmento ser´ trivialmente aceito e tra¸ado.
o ca a c
Figura 7.3: Funcionamento do algoritmo de Cohen-Sutherland para recorte de segmentos.
80

82. A linha EI requer mais itera¸˜es. O primeiro extremo, E, tem c´digo 0100 e ´ escolhido pelo algoritmo
co o e
como ponto externo. O c´digo ´ testado para obter a primeira aresta que a linha cruza, no caso a aresta
o e
inferior, e EI ´ recortado para FI. Na segunda itera¸˜o, FI n˜o pode ser trivialmente aceito ou rejeitado.
e ca a
O c´digo da primeira extremidade, F, ´ 0000, de forma que o algoritmo escolhe o ponto externo I, cujo
o e
c´digo ´ 1010. A primeira aresta interceptada ´ a superior, resultando no segmento FH. O c´digo de H
o e e o
´ 0010, e a terceira itera¸˜o resulta num corte pela aresta direita. O segmento resultante ´ trivialmente
e ca e
aceito e tra¸ado na quarta itera¸˜o. O Algoritmo 7.1 e 7.2 ilustram este procedimento.
c ca
Este algoritmo n˜o ´ o mais eficiente - como os testes e recorte s˜o executados numa ordem fixa,
a e a
eventualmente ser˜o feitos recortes desnecess´rios. Por exemplo, quando a intersec¸˜o com uma aresta
a a ca
do retˆngulo ´ uma “intersec¸˜o externa”, que n˜o est´ na fronteira do retˆngulo de visualiza¸˜o (ponto
a e ca a a a ca
H na linha EI, Figura 7.4). Existem algoritmos mais eficientes (v. Foley, 3.12), mas este ainda ´ o mais
e
utilizado, por ser simples e bastante conhecido.
typedef enum {LEFT = 0, RIGHT = 1, BOTTOM = 2, TOP = 3} aresta;
typedef enum {TRUE, FALSE} boolean;
typedef boolean outcode;
/* Retorna TRUE se todos os outcodes em codigo sao FALSE, e
* FALSE c.c. */
boolean Vazio(outcode codigo[]);
/* Retorna TRUE se a interseccao logica entre codigo1 e codigo
* 2 e vazia, e FALSE c.c. */
boolean InterseccaoVazia(outcode codigo0[], outcode codigo1 []);
/* Retorna TRUE se codigo0 e codigo 1 sao iguais, e FALSE c.c. */
boolean Igual(outcode codigo0[], outcode codigo1[]);
/* Calcula outcode para ponto (x,y) */
void CalculaOutCode(float x, float y, outcode codigo[]) {
int i;
for (i - LEFT; i < = TOP; i++)
codigo[i] = FALSE;
/* Fim for */
if (y > YMAX)
codigo[TOP] = TRUE;
else if (y < YMIN)
codigo[BOTTOM] = TRUE;
/* Fim se */
if (x > xmax)
codigo[RIGHT] = TRUE;
else if (x < xmax)
codigo[BOTTOM] = TRUE;
/* Fim Se */
}/* End CalculaOutCode */
Algoritmo 7.1: Calculando os c´digos do algoritmo de Cohen-Sutherland.
o
7.2 Recorte de Circunferˆncias
e
Para recortar uma circunferˆncia contra um retˆngulo, podemos primeiro executar um teste de aceita¸˜o/rejei¸˜o
e a ca ca
trivial interceptando a extens˜o da circunferˆncia (um quadrado do tamanho do diˆmetro da circun-
a e a
ferˆncia) com o retˆngulo de visualiza¸˜o usando o algoritmo para recorte de pol´
e a ca ıgonos que ser´ visto a se-
a
guir. Se a circunferˆncia intercepta o retˆngulo, ela ´ subdivida em quadrantes, e testes de aceita¸˜o/rejei¸˜o
e a e ca ca
a ´
trivial s˜o feitos para cada um. Estes testes podem levar a testes por octantes. E poss´ ent˜o calcular
ıvel a
a intersec¸˜o da circunferˆncia e da aresta analiticamente, resolvendo suas equa¸˜es simultaneamente, e
ca e co
a seguir fazer a convers˜o matricial dos arcos resultantes. Se a convers˜o matricial ´ r´pida, ou se a cir-
a a e a
cunferˆncia n˜o ´ muito grande, seria provavelmente mais eficiente usar a t´cnica de scissoring, testando
e a e e
cada pixel na circunferˆncia contra os limites do retˆngulo antes de tra¸´-lo.
e a ca
Um algoritmo para recorte de pol´ ıgonos precisa tratar de muitos casos distintos, como mostra a Figura
7.5. O caso (a) ´ particularmente interessante porque um pol´
e ıgono cˆncavo ´ recortado em dois pol´
o e ıgonos
81

83. /* algoritmo de recorte de Cohen-Sutherland para linha P0(x0,y0) a
* P1(x1,y1), e retangulo de recorte com diagonal de (xmin,ymin) a
* (xmax,ymax). */
void RecorteLinhaCohenSutherland(float x0,float y0,float x1,float y1,int valor){
boolean aceito, pronto;
outcode outcode0[4], outcode1 [4], *outcode0ut; /* outcodes para P0, P1 e
quaisquer outros pontos que
estao fora do retangulo de
recorte */
float x, y;
aceito = FALSE; pronto = FALSE;
CalculaOutCode(x0,y0,outcode0); CalcuiaOutCode(xl ,y1 ,outcode1);
do {
if (vazio(outcode0) && vazio(outcode1)){
/* aceitacao trivial e sai */
aceito = TRUE;
pronto = TRUE;
}else if (interseccao_vazia(outcode0,outcode1))
/* rejeicao trivial e sai */
pronto = TRUE;
else {
/* ambos os testes falharam, entao calcula o segmento de
reta a recortar: a partir de um ponto externo a uma
interseccao com a aresta de recorte */
/* pelo menos um ponto esta fora do retangulo de recorte;
seleciona-o */
outcode0ut= vazio(outcode0) ? outcode1 : outcode0;
/* acha agora o ponto de interseccao, usando as formulas:
y = y0 + inclinacao * (x-x0), x = x0 + ( 1 /inclinacao) * (y-y0) */
if (outcodeOut(TOP)) {
/* divide a linha no topo do retangulo de recorte */
x= x0 + (x1-x0) * (ymax-y0)/(y1-y0); y= ymax;
}else if (outcode0ut[BOTTOM]) {
/* divide a linha na base do retangulo de recorte */
x = x0 + (x1-x0) + (ymin-y0)/(y1-y0); y = ymin;
}else if (outcode0ut[RIGHT]) {
/* divide a linha na aresta direita do retangulo de recorte */
y = y0 + (y1 -y0) + (xmax-x0)/(x1-x01; x = xmax;
}else if (outcode0ut[LEFT]) {
/* divide a linha na aresta esquerda do retangulo de recorte */
y = y0 + (y 1 -y0) + (xmin-x0)/(x1-x0); x = xmin;
} /* Fim se */
/* agora move o ponto externo para o ponto de interseccao, para
recortar e preparar para o proximo passo */
if (igual(outcode0ut,outcode0)) {
x0 = x; y0 = y; CalculaOutCode(x0,y0,outcode0);
}else{
x1 = x; y1 = y; CalculaOutCode(x1,y1,outcode1);
}
}/* fim do else da subdivisao */
} while (pronto);
if (aceito)
MeioPontoLinhaReal(x0,y0,x1,y1),valor); /* versao do algoritmo para coordenadas reais */
} /* fim do algoritmo de recorte e tracado */
Algoritmo 7.2: Desenhando a linha com o algoritmo de Cohen-Sutherland. Algumas das fun¸˜es
co
usadas est˜o ilustradas no Algoritmo 7.2.
a
82

84. Figura 7.4: Algoritmo de Sutherland-Hodgman para Recorte de Pol´
ıgonos.
Figura 7.5: Exemptos de recorte de pol´ıgonos. (a) M´ltiplos componentes. (b) Caso convexo (c) Caso
u
cˆncavo com muitas arestas exteriores.
o
separados. O problema ´ complexo porque cada aresta do pol´
e ıgono precisa ser testada contra cada aresta
do retˆngulo de visualiza¸˜o; novas arestas precisam ser acrescentadas, arestas existentes precisam ser
a ca
descartadas, mantidas ou subdivididas. V´rios pol´
a ıgonos podem resultar do recorte de um unico, e ´
´ e
necess´rio uma abordagem organizada para tratar todos os caso poss´
a ıveis.
O algoritmo para recorte de pol´ ıgonos de Sutherland-Hodgman usa a estrat´gia “dividir para conquis-
e
tar”; resolve uma s´rie de problemas simples e idˆnticos cujas solu¸˜es, quando combinadas, resolvem o
e e co
problema todo. O problema b´sico consiste em recortar o pol´
a ıgono contra uma unica aresta de recorte
´
infinita. Quatro arestas, cada qual definindo um lado do retˆngulo, recortam o pol´
a ıgono sucessivamente
contra o retˆngulo de visualiza¸˜o.
a ca
Note a diferen¸a entre esta estrat´gia para um pol´
c e ıgono e o algoritmo de Cohen-Sutherland para
recorte de linhas: O algoritmo para pol´ ıgonos recorta quatro arestas sucessivamente, enquanto que o
algoritmo para linhas testa o c´digo para verificar qual aresta ´ interceptada, e recorta apenas quando
o e
necess´rio. O algoritmo de Sutherland-Hodgman ´ na verdade mais geral: um pol´
a e ıgono (cˆncavo ou
o
convexo) pode ser recortado contra qualquer pol´ ıgono de recorte convexo. Em 3D, pol´ ıgonos podem ser
recortados contra volumes poliedrais convexos definidos por planos. O algoritmo aceita como entrada
uma s´rie de v´rtices v1, v2, ..., vn que, em 2D, definem as arestas de um pol´
e e ıgono. A seguir, recorta
o pol´ıgono contra uma unica aresta de recorte infinita, e retorna outra s´rie de v´rtices que definem o
´ e e
pol´
ıgono recortado. Num segundo passo, o pol´ ıgono parcialmente recortado ´ recortado novamente contra
e
a segunda aresta, e assim por diante.
O algoritmo movimenta-se em torno do pol´ ıgono, indo do v´rtice vn ao v´rtice v1, e de volta a vn,
e e
examinando a cada passo a rela¸˜o entre um v´rtice e a aresta de recorte. Em cada passo, zero, um ou
ca e
dois v´rtices s˜o adicionados ` lista de sa´ dos v´rtices que definem o pol´
e a a ıda e ıgono recortado, dependendo
83

85. da posi¸˜o do v´rtice sendo analisado em rela¸˜o ` aresta de recorte.
ca e ca a
Figura 7.6: Quatro situa¸˜es poss´
co ıveis no recorte de pol´
ıgonos.
S˜o quatro situa¸˜es poss´
a co ıveis (Figura 7.6). Consideremos uma aresta do pol´ ıgono que vai do v´rtice
e
s ao v´rtice p. Suponha que o v´rtice s foi analisado na itera¸˜o anterior, e a intera¸˜o corrente est´
e e ca ca a
analisando p. No caso 1 , a aresta do pol´ ıgono est´ completamente dentro da fronteira do retˆngulo de
a a
visualiza¸˜o, e o v´rtice p ´ adicionado ` lista de sa´
ca e e a ıda. No caso 2, o ponto i, que define a intersec¸˜o
ca
entre a aresta do pol´ıgono e a aresta do retˆngulo, ´ colocado como um v´rtice na lista de sa´
a e e ıda. No caso
3, ambos os v´rtices est˜o fora do retˆngulo, e nenhum ´ colocado na lista de sa´
e a a e ıda. No caso 4, ambos os
pontos i (intersec¸˜o) e p, s˜o colocados na lista de sa´
ca a ıda.
O procedimento, mostrado no Algoritmo 7.3, aceita um vetor de v´rtices, inVertexArray, e cria outro
e
vetor outVertexArray. Para manter o c´digo simples, n˜o inclu´
o a ımos verifica¸˜o dos erros nos limites dos
ca
vetores, e usamos o procedimento Output() para incluir um v´rtice em outVertexArray. O procedimento
e
Intersect() calcula a intersec¸˜o de uma aresta s -¿p do pol´
ca ıgono com a aresta clipBoundary, definida
por dois v´rtices da fronteira do pol´
e ıgono de recorte. A fun¸˜o Inside() retorna true se o v´rtice est´
ca e a
no interior da fronteira de recorte. Assume-se que o v´rtice est´ no interior da fronteira se estiver “a
e a
esquerda da aresta de recorte, quando olha-se do primeiro para o segundo v´rtice da aresta”. Esta
e
orienta¸˜o corresponde a uma enumera¸˜o das arestas no sentido anti-hor´rio. Para calcular se um ponto
ca ca a
est´ fora da fronteira de recorte, podemos testar o sinal do produto vetorial do vetor normal ` fronteira
a a
de recorte e da aresta do pol´ıgono.
0 algoritmo ´ bastante geral, e pode ser estruturado para chamar a si pr´prio recursivamente de uma
e o
forma que o torna bastante eficiente para implementa¸˜o em hardware.
ca
84

86. /* Algoritmo de Sutherland-Hodgman para recorte do pol´gonos */
ı
#define MAX 20
typedef struct {float x,y;} ponto;
typedef ponto vertice;
typedef vertice aresta[2];
typedef vertice VetorVertices[MAX];
typedef enum {TRUE = 1, FALSE = 0} boolean;
/* Acrescenta um novo vertice a vetorSaida, e atualiza tamSaida */
void saida(vertice novoVertice, int *tamSaida, VetorVertices vetorSaida);
/* Checa se o vertice esta dentro ou fora da aresta de recorte */
boolean dentro(vertice testeVertice, aresta arestaRecorte);
/* recorta a aresta (prim,seg) do poligono contra arestaRecorte,
* retorna o novo ponto */
vertice intercepta(vertice prim, vertice seg, aresta arestaRecorte);
void RecortePoligonosSutherlandHodgman(
VetorVertices vetorEntrada, /* vetor de vertices de entrada */
VetorVertices vetorSaida, /* vetor de vertices de saida */
int tamEntrada, /* numero de entradas em vetorEntrada */
int tamSaida, /* numero de vertices em vetorSaida */
aresta arestaRecorte /* aresta do poligono de recorte */){
vertice s, p; /* pontos inicial e final da aresta de recorte corrente */
vertice i; /* ponto de interseccao com uma aresta de recorte */
int j; /* contador para o loop de vertices */
*tamSaida = 0;
s = vetorEntrada[tamEntrada]; / * comeca com o ultimo vertice em vetorEntrada */
for (j = 1 ;j < = tamEntrada;j + + ) {
p= vetorEntrada[j]; /* agora s e p correspondem aos vertices na Fig. */
if (dentro(s,arestaRecorte)) {
/* casos 1 e 4 */
if (dentro(s,arestaRecorte))
saida(p,tamSaida,vetorSaida);
else {
i = intercepta(s,p,arestaRecorte);
saida(i,tamSaida,vetorSaida);
saida(p,tamSaida,vetorSaida);
}/* Fim Se */
}else{
/* casos 2 e 3 */
if (dentro(s,arestaRecorte)) {
i = intercepta(s,p,arestaRecorte);
saida(i,tamSaida,vetorSaida);
}/* Fim Se */
}/*Fim Se */
s = p;
}/* fim do for */
}/* fim do algoritmo de recorte */
Algoritmo 7.3: Algoritmo de Cohen-Sutherland.
85

87. Cap´
ıtulo 8
Curvas e Superf´
ıcies em Computa¸˜o
ca
Gr´fica
a
Curvas e superf´
ıcies tridimensionais (espaciais) desempenham um papel importante:
• na engenharia, projeto e manufatura de uma ampla gama de produtos, como autom´veis, cascos de
o
navios, fuselagem e asas de avi˜es, lˆminas de propuls˜o, sapatos, garrafas, edifica¸˜es, etc.
o a a co
• na descri¸˜o e interpreta¸˜o de fenˆmenos f´
ca ca o ısicos em ´reas como geologia, f´
a ısica e medicina.
• Projeto Geom´trico Apoiado por Computador (Computer Aided Geometric Design): nova
e
disciplina que incorpora modelos matem´ticos e computacionais desenvolvidos para apoiar os pro-
a
cessos de engenharia, projeto e manufatura.
Frequentemente, superf´
ıcies s˜o descritas por uma malha de curvas definidas em planos ortogonais
a
(Figura 8.1). As curvas podem ser obtidas atrav´s da digitaliza¸˜o de um modelo f´
e ca ısico ou desenho, e
posterior ajuste de uma curva matem´tica aos pontos digitalizados, ou geradas a partir de formula¸˜es
a co
criadas especificamente para a defini¸˜o de curvas no espa¸o.
ca c
Figura 8.1: Representa¸˜o de superf´
ca ıcies atrav´s de malhas.
e
8.1 Representa¸˜o de Curvas
ca
Existem duas formas alternativas de representa¸˜o:
ca
• por um conjunto de pontos: nesse caso, uma representa¸˜o visual adequada pode ser gerada
ca
conectando-se os pontos por segmentos de reta, se estes forem espa¸ados adequadamente (Figura
c
??). Observe que nas regi˜es da curva onde a curvatura ´ grande, a proxima¸˜o por segmentos de
o e ca
86

88. reta ´ particularmente ruim (Figura ??(a)). Uma maneira de melhorar a representa¸˜o ´ aumentar
e ca e
a densidade dos pontos nessas regi˜es (Figura ??(b)).
o
• anal´
ıtica: ou seja, atrav´s de formula¸˜es matem´ticas, o que apresenta v´rias vantagens em rela¸˜o
e co a a ca
a
` representa¸˜o anterior:
ca
• precis˜o,
a
• armazenagem compacta,
• facilidade de c´lculo (exato) de pontos intermedi´rios (em uma representa¸˜o por pontos pontos
a a ca
intermedi´rios precisam ser determinados por interpola¸˜o),
a ca
• facilidade para calcular propriedades da curva como inclina¸˜o e curvatura (em uma representa¸˜o
ca ca
por pontos tais propriedades precisam ser calculadas por diferencia¸˜o num´rica, um procedimento
ca e
que ´ pouco preciso),
e
• facilidade para desenhar as curvas,
• facilidade para fazer altera¸˜es cont´
co ınuas no formato da curva de forma a atender requisitos de
projeto (“design”).
Figura 8.2: Aproxima¸˜o de curvas por segmentos de reta conectados.
ca
8.2 Curve Fitting x Curve Fairing
8.2.1 Ajuste de curvas (curve fitting)
Frequentemente, deseja-se obter representa¸˜es anal´
co ıticas para curvas definidas originalmente por con-
juntos de pontos - por exemplo, pontos em uma curva ou superf´ real foram digitalizados. Do ponto
ıcie
de vista matem´tico, esse ´ um problema de interpola¸˜o. Uma curva que ajusta (fit) os pontos da-
a e ca
dos passa por todos esses pontos. Uma t´cnica usual de ajuste de curvas s˜o as splines c´ bicas, uma
e a u
estrat´gia de aproxima¸˜o polinomial por partes.
e ca
8.2.2 Aproxima¸˜o de curvas (curve fairing)
ca
Se os pontos dados s˜o aproxima¸˜es para valores desconhecidos, por exemplo, s˜o pontos coletados ou
a co a
obtidos em medidas experimentais, ent˜o o que se deseja ´ uma curva que mostre a tendˆncia dos dados.
a e e
Em geral, a curva obtida pode n˜o passar por nenhum dos pontos dados, e diz-se que a curva aproxima
a
(fair ) os dados. Alternativamente, pode-se desejar gerar uma descri¸˜o matem´tica de uma curva no
ca a
espa¸o sem qualquer conhecimento pr´vio da forma da curva. Para esse caso, t´cnicas usuais s˜o as
c e e a
representa¸˜es de B´zier e B-splines (ambas s˜o estrat´gias de aproxima¸˜o de curvas).
co e a e ca
8.3 Representa¸˜es Param´tricas e N˜o Param´tricas (expl´
co e a e ıcita
e impl´
ıcita)
Para uma curva plana, a forma n˜o param´trica expl´
a e ıcita ´ dada por
e
y = f (x) (8.1)
por exemplo, a equa¸˜o de uma linha reta ´ dada por
ca e
87

89. y = mx + b (8.2)
Desta forma, obt´m-se um valor de y para cada valor de x dado. Consequentemente, curvas fechadas,
e
ou com valores m´ltiplos, como um c´
u ırculo, n˜o podem ser representadas explicitamente. Essa limita¸˜o
a ca
n˜o existe no caso de representa¸˜es impl´
a co ıcitas, na forma
f (x, y) = 0 (8.3)
A equa¸˜o impl´
ca ıcita de segundo grau gen´rica:
e
ax2 + 2bxy + cy 2 + 2dx + 2ey + f = 0 (8.4)
engloba uma variedade de curvas bi-dimensionais denominadas se¸˜es cˆnicas. Os trˆs tipos de
co o e
se¸˜es cˆnicas s˜o a par´bola, a hip´rbole e a elipse (um c´
co o a a e ırculo ´ um caso especial de uma elipse)
e
(Figura ??).
Figura 8.3: Aproxima¸˜o de curvas por segmentos de reta conectados.
ca
Dependendo dos valores de a, b, c, d, e e f , diferentes tipos de se¸˜es cˆnicas s˜o produzidas. Se a
co o a
se¸˜o cˆnica ´ definida em rela¸˜o a um sistema de coordenadas local e passa pela origem, ent˜o f = 0.
ca o e ca a
8.3.1 Limita¸˜es das representa¸˜es n˜o param´tricas
co co a e
• Ambas (expl´ ıcita e impl´ıcita) s˜o dependentes do sistema de coordenadas, cuja escolha afeta a
a
facilidade de uso. Por exemplo, surgem problemas se no sistema de coordenadas escolhido for
necess´ria uma inclina¸˜o infinita como condi¸˜o de contorno, pois essa inclina¸˜o n˜o pode ser
a ca ca ca a
usada diretamente como uma condi¸˜o de contorno num´rica. Ou o sistema de coordenadas ´
ca e e
alterado, ou a inclina¸˜o infinita ser´ representada numericamente por um valor muito grande,
ca a
positivo ou negativo.
88

90. • pontos em uma curva calculados a partir de incrementos uniformes em x ou y n˜o est˜o distribu´
a a ıdos
uniformemente ao longo da curva, o que afeta a qualidade e precis˜o de uma representa¸˜o gr´fica.
a ca a
Estas limita¸˜es s˜o superadas pelo uso de representa¸˜es param´tricas.
co a co e
Na forma param´trica, cada coordenada de um ponto em uma curva ´ representada como uma fun¸˜o
e e ca
de um unico parˆmetro, sendo que a posi¸˜o de um ponto na curva ´ fixada pelo valor do parˆmetro.
´ a ca e a
Para uma curva 2D que usa t como parˆmetro, as coordenadas cartesianas de um ponto na curva s˜o:
a a
x = x(t)
y = y(t) (8.5)
O vetor que define a posi¸˜o de um ponto na curva ´ portanto dado por
ca e
P (t) = [ x(t) y(t) ] (8.6)
A derivada, ou vetor tangente da curva ´ dada por
e
P (t) = [ x (t) y (t) ] (8.7)
A inclina¸˜o da curva ´ dada por
ca e
dx
dx dt x (t)
= dy
= (8.8)
dy dt
y (t)
Observa¸˜es
co
• A forma param´trica ´ adequada para representar curvas fechadas e com valores m´ltiplos. A forma
e e u
n˜o param´trica pode ser obtida eliminando-se o parˆmetro para obter uma unica equa¸˜o em x e
a e a ´ ca
y.
• Uma vez que um ponto na curva ´ especificado por um unico valor de parˆmetro, a forma pa-
e ´ a
ram´trica ´ independente do sistema de coordenadas. Os extremos e o comprimento da curva s˜o
e e a
fixos pelo intervalo de varia¸˜o do parˆmetro, frequentemente normalizado para , por conveniˆncia.
ca a e
Como as curvas s˜o independentes do sistema de coordenadas, elas s˜o facilmente manipuladas
a a
usando as transforma¸˜es geom´tricas afins (ver Cap´
co e ıtulo 5).
• Determinar um ponto em uma curva, i.e., determinar o valor de y, dado x, ´ trivial no caso da
e
representa¸˜o expl´
ca ıcita. No caso da param´trica, ´ necess´rio obter o valor do parˆmetro t, a partir
e e a a
de x, e a seguir usar este valor para obter y. (Para equa¸˜es param´tricas mais complexas, uma
co e
t´cnica iterativa pode ser mais conveniente).
e
• Ambas as formas de representa¸˜o tˆm vantagens e desvantagens em situa¸˜es espec´
ca e co ıficas!
Exemplos:
1. segmento de reta
Para 2 vetores que especificam as posi¸˜es iniciais P1 e P2, uma representa¸˜o param´trica do
co ca e
segmento ´ dada por
e
Como P (t) ´ um vetor de posi¸˜o, cada um de seus componentes tem uma representa¸˜o param´trica
e ca ca e
x(t) e y(t) entre P 1 e P 2.
2. C´
ırculo no primeiro quadrante
Uma compara¸˜o das representa¸˜es visuais obtidas a partir das formas param´trica e n˜o-param´trica
ca co e a e
para um c´ırculo no primeiro quadrante ´ apresentada na Figura 8.4 (observe que a representa¸˜o
e ca
param´trica para uma curva n˜o ´ unica!)
e a e´
Os pontos na circunferˆncia mostrados nas Figuras 8.4(b) e 8.4(c) foram obtidos com intervalos
e
constantes dos parˆmetros q e t, respectivamente. A primeira representa¸˜o produz comprimentos
a ca
de arcos idˆnticos ao longo da circunferˆncia, ao contr´rio da segunda (a qual, entretanto, tem
e e a
aparˆncia visual melhor que a mostrada em 8.4(a), gerada pela representa¸˜o expl´
e ca ıcita). Por outro
lado, o c´lculo das fun¸˜es trigonom´tricas ´ computacionalmente caro, de maneira que a segunda
a co e e
forma de representa¸˜o param´trica representa um meio termo entre a forma expl´
ca e ıcita e a forma
param´trica padr˜o.
e a
89

91. Figura 8.4: Pontos de uma circunferˆncia.
e
8.4 Curvas de B´zier
e
T´cnicas de aproxima¸˜o de curvas s˜o muito usadas em ambientes de projeto (CAD) interativos, por
e ca a
serem mais intuitivas do que as t´cnicas de ajuste. Um m´todo adequado para o design de curvas e
e e
superf´
ıcies de forma-livre em ambientes interativos foi desenvolvido por Pierre B´zier. Uma curva de
e
B´zier ´ determinada por um pol´
e e ıgono de defini¸˜o (Figuras 8.5 e ??).
ca
Figura 8.5: Representa¸˜o de uma curva de B´zier definida pelos pontos B0 , B1 , B2 e B3 .
ca e
Matematicamente, uma curva de B´zier param´trica ´ definida como
e e e
n
P (t) = Bi Jn,i (t) 0≤t≤1 (8.9)
i=0
onde as fun¸˜es de blending, ou fun¸˜es base de B´zier s˜o
co co e a
n
Jn,i (t) = ti (1 − t)n−i (8.10)
i
com
n n!
= (8.11)
i i!(n − i)!
Jn,i (t) ´ a i-´sima fun¸˜o base de Bernstein de ordem n, onde n, o grau da fun¸˜o-base, e portanto
e e ca ca
do segmento de curva polinomial, ´ um menos o n´mero de pontos do pol´
e u ıgono de defini¸˜o. Os v´rtices
ca e
do pol´
ıgono s˜o numerados de 0 a n (como na Figura 8.5). A Figura 8.6 mostra as fun¸˜es de blending
a co
90

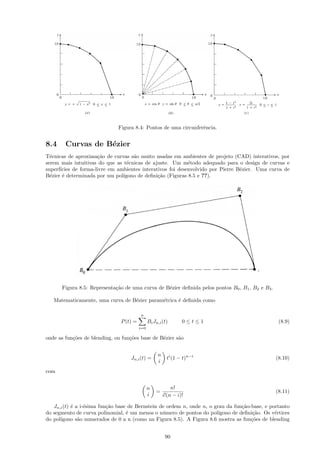
92. Figura 8.6: Fun¸˜es de blending para v´rios valores de n.
co a
para v´rios valores de n. Observe a simetria das fun¸˜es. Examinando-se as Equa¸˜es 8.9 a 8.11 para o
a co co
primeiro ponto na curva, i.e., em t = 0, verifica-se que
Jn,0 (0) = 1 i=0
Jn,i (0) = 0 i=0
(8.12)
Portanto,
P (0) = B0 Jn,0 (0) = B0 (8.13)
e o primeiro ponto na curva coincide com o primeiro ponto do pol´ ıgono de controle. Verifica¸˜o an´loga
ca a
pode ser feita para o ultimo ponto, i.e., em t = 1. As fun¸˜es base da Figura 8.6 ilustram estes resultados.
´ co
Al´m disso, pode-se mostrar que para qualquer valor do parˆmetro t, o somat´rio das fun¸˜es base ´
e a o co e
1, i.e.,
n
Jn,i = 1 (8.14)
i=0
A equa¸˜o para uma curva de B´zier pode ser expressa na forma matricial como
ca e
P (t) = T N G = F G (8.15)
onde F = Jn,0 Jn,1 · · · Jn,n e Gr = B0 B1 · · · Bn .
As matrizes espec´ıficas para valores pequenos de n (n = 3, 4) s˜o de particular interesse. Para qualquer
a
valor de n, a matriz [N] ´ sim´trica em rela¸˜o ` diagonal principal e o canto triangular inferior direito
e e ca a
cont´m apenas zeros.
e
Em geral, uma forma complexa n˜o pode ser modelada por uma unica curva, mas por v´rias curvas
a ´ a
que s˜o conectadas em seus pontos extremos. Ao criar as jun¸˜es, o projetista, em geral, deseja controlar
a co
91

93. a continuidade nos pontos de jun¸˜o. Continuidade de ordem 0 significa que as 2 curvas se encontram;
ca
continuidade de primeira ordem exige que as curvas sejam tangentes no ponto de jun¸˜o, e continuidade
ca
de segunda ordem exige que as curvaturas sejam as mesmas.
A formula¸˜o de B´zier apresenta v´rias propriedades interessantes:
ca e a
• As fun¸˜es-base s˜o reais.
co a
• O grau do polinˆmio que define uma curva ´ um menos o n´mero de pontos do pol´
o e u ıgono de defini¸˜o.
ca
• A forma da curva geralmente acompanha a forma do pol´ ıgono de defini¸˜o (na verdade ´ uma vers˜o
ca e a
“suavizada” da forma do pol´ ıgono (v. Fig. 3.3)). Assim, para desenhar uma curva, basta definir o
pol´
ıgono e depois ajustar os pontos que forem necess´rios para aproximar melhor a forma desejada.
a
Isso torna a formula¸˜o adequada para o design interativo. Um projetista experiente consegue obter
ca
a forma desejada depois de 2 ou 3 intera¸˜es com um sistema computacional.
co
• O primeiro e ultimo pontos da curva coincidem com o primeiro e ultimo pontos do pol´
´ ´ ıgono de
defini¸˜o. Em situa¸˜es pr´ticas, em geral ´ desej´vel ter controle direto sobre os pontos extremos
ca co a e a
da curva.
• Os vetores tangentes nos extremos da curva tˆm a mesma dire¸˜o que o primeiro e o ultimo seg-
e ca ´
mentos do pol´ıgono de defini¸˜o, respectivamente.
ca
• A curva est´ contida no fecho convexo do pol´
a ıgono de defini¸˜o, i.e., no maior pol´
ca ıgono convexo que
pode ser obtido com os v´rtices do pol´
e ıgono de defini¸˜o (Figura 8.5). Uma consequˆncia simples
ca e
deste fato ´ que um pol´
e ıgono plano sempre gera uma curva plana.
A importˆncia desta propriedade est´ principalmente no contexto de verifica¸˜o de interferˆncia.
a a ca e
Suponha que desejamos saber se 2 curvas se interceptam. Por exemplo, cada uma representa o
caminho a ser percorrido pelo bra¸o de um robˆ, e nosso objetivo ´ garantir que os caminhos n˜o se
c o e a
interceptam, evitando colis˜es. Ao inv´s de tentar calcular uma poss´ intersec˜o, podemos fazer
o e ıvel a
um teste muito mais barato: envolver o pol´ ıgono de controle no menor retˆngulo que o cont´m
a e
e cujas arestas s˜o paralelas a um sistema de coordenadas (minmax boxes). O retˆngulo cont´m
a a e
o pol´ıgono de controle e, pela propriedade do fecho convexo, cont´m tamb´m a curva. Verficar
e e
se os 2 retˆngulos se interceptam ´ um teste trivial, e fica simples checar a n˜o-intersec¸˜o. Se
a e a ca
houver intersec¸˜o dos retˆngulos, mais verifica¸˜es precisam ser feitas nas curvas. A possibilidade
ca a co
de detectar n˜o-interferˆncia de forma r´pida ´ muito importante, pois na pr´tica ´ freq¨ente que
a e a e a e u
tais testes precisem ser feitos milhares de vezes para cada objeto.
• A curva exibe a propriedade da varia¸˜o decrescente (variation diminishing property). Isto significa,
ca
basicamente, que a curva n˜o oscila em rela¸˜o a qualquer linha reta com mais frequˆncia que o
a ca e
pol´
ıgono de defini¸˜o. Algumas representa¸˜es matem´ticas tˆm a tendˆncia de amplificar, ao inv´s
ca co a e e e
de suavizar, quaisquer irregularidades de formato esbo¸adas pelos pontos de defini¸˜o, enquanto
c ca
que outras, como as curvas de B´zier, sempre suavizam os pontos de controle. Assim, a curva nunca
e
cruza uma linha reta arbitr´ria mais vezes que a sequˆncia de segmentos que conectam os pontos
a e
de controle (v. Fig.)
• A curva ´ invariante sob transforma¸˜es afins. Transforma¸˜es afins est˜o dispon´
e co co a ıveis em qualquer
sistema de CAD, pois ´ essencial reposicionar, escalar, etc. os objetos. Esta propriedade garante
e
que os 2 procedimentos abaixo produzem os mesmos resultados: a) primeiro calcula um ponto na
curva, e depois aplica a ele uma transforma¸˜o afim; e b) primeiro, aplica uma transforma¸˜o afim
ca ca
ao pol´
ıgono de defini¸˜o, e depois gera o ponto na curva.
ca
Uma consequˆncia pr´tica: suponha que tra¸amos uma curva c´bica calculando 100 pontos sobre ela;
e a c u
e que agora queremos desenhar a mesma curva depois de uma rota¸˜o. Podemos aplicar a rota¸˜o a
ca ca
cada um dos 100 pontos, e desenhar os pontos resultantes, ou aplicar a rota¸˜o a cada um dos 4 pontos
ca
do pol´
ıgono de controle, calcular novamente os 100 pontos e tra¸´-los. A primeira estrat´gia requer que
ca e
ca ca ´
a rota¸˜o seja aplicada 100 vezes, e a segunda requer a sua aplica¸˜o apenas 4 vezes! E interessante
observar que as curvas de B´zier n˜o s˜o invariantes sob transforma¸˜es projetivas.
e a a co
Bibliografia
Fonte: Caps. 4,5 Rogers & Adams - Mathematical Elements for Computer Graphics
92

94. Cap´
ıtulo 9
Apostila Modelagem
O texto sobre modelagem pode ser encontrado no seguinte endere¸o:
c
http://gbdi.icmc.usp.br/documentacao/apostilas/cg/downloads/modelagem.pdf
93

95. Cap´
ıtulo 10
Rendering
Esta apostila est´ sob revis˜o e ser´ adicionada nesta vers˜o assim que poss´
a a a a ıvel. A vers˜o anterior pode
a
ser encontrada em:
http://gbdi.icmc.usp.br/∼cg/ap10.html
94

96. Cap´
ıtulo 11
Cores e Sistemas de Cores
11.1 Percep¸˜o de Cor
ca
A cor ´ o atributo da percep¸˜o visual que pode ser descrito atrav´s dos nomes usados para identificar as
e ca e
cores, como branco, cinza, preto, amarelo, etc., ou da combina¸˜o delas. As diferentes cores, ou espectros
ca
luminosos, que podem ser percebidos pelo sistema visual humano correspondem a uma pequena faixa de
freq¨ˆncias do espectro eletromagn´tico, que inclui as ondas de r´dio, microondas, os raios infravermelhos
ue e a
e os raios X, como mostrado na Figura 11.1.
Figura 11.1: Espectro eletromagn´tico [Gro94].
e
A freq¨ˆncia mais baixa do espectro vis´
ue ıvel corresponde ` cor vermelha (4.3 × 1014 hertz) e a mais
a
14
alta ` cor violeta (7.5 × 10 hertz). Os valores de freq¨ˆncia intermedi´rios correspondem a cores que
a ue a
passam pelo alaranjado e amarelo e por todas as outras cores, at´ chegar nos verdes e azuis. As cores
e
s˜o ondas eletromagn´ticas descritas pelo seu comprimento de onda (l) e especificadas, tipicamente, em
a e
nanˆmetros (nm).
o
Os comprimentos de onda maiores possuem distˆncias focais maiores e, conseq¨entemente, requerem
a u
maior curvatura da lente do olho para serem focalizados, (a cor vermelha possui a maior distˆncia focal
a
e a azul, a menor). A utiliza¸˜o simultˆnea de cores localizadas em extremos opostos do espectro fazem
ca a
com que a lente altere o seu formato constantemente, causando cansa¸o no olho. A vis˜o estereosc´pica
c a o
da cor ´ um efeito relacionado ao processo de focaliza¸˜o da imagem na retina, que faz com que cores
e ca
puras localizadas ` mesma distˆncia do olho pare¸am estar a distˆncias diferentes; por exemplo, a cor
a a c a
vermelha parece estar mais pr´xima e a cor azul parece estar mais distante.
o
Uma fonte de luz (como, por exemplo, o sol ou uma lˆmpada) emite em todas as freq¨ˆncias do
a ue
espectro vis´ ıvel, produzindo a luz branca que incide sobre um objeto. Parte dessa luz ´ absorvida e a outra
e
parte ´ refletida, determinando a cor resultante do objeto. Quando h´ predominˆncia das freq¨ˆncias
e a a ue
baixas, diz-se que o objeto ´ vermelho, ou que a luz percebida possui uma freq¨ˆncia dominante (ou um
e ue
comprimento de onda dominante) na freq¨ˆncia baixa do espectro. A freq¨ˆncia dominante tamb´m ´
ue ue e e
chamada de matiz ou, simplesmente, de cor da luz.
O matiz ´ o atributo de uma sensa¸˜o visual que faz com que uma ´rea pare¸a ser similar a uma
e ca a c
ou 2 das cores percebidas vermelha, amarela, laranja, azul, p´rpura [Hun78]. A partir dessa defini¸˜o,
u ca
pode-se diferenciar a cor crom´tica, que possui matiz, da acrom´tica, que ´ desprovida de matiz. As
a a e
caracter´ ısticas da luz s˜o descritas atrav´s de propriedades como o matiz e as sensa¸˜es de brilho e
a e co
satura¸˜o. O matiz ´ usado para dar um nome a uma cor, o brilho corresponde ao grau de luminˆncia
ca e a
95

97. de uma cor em rela¸˜o ` luminˆncia de outra ou em rela¸˜o ao fundo, e a satura¸˜o ´ a pureza aparente
ca a a ca ca e
de um matiz. Quanto maior o dom´ ınio de um comprimento de onda, maior ´ a sua satura¸˜o. As cores
e ca
preta, branca e cinza possuem satura¸˜o uniforme em todos os comprimentos de onda e, por isso, s˜o
ca a
diferenciadas apenas pelo brilho. As propriedades de satura¸˜o e de matiz de uma cor s˜o referenciadas
ca a
como cromaticidade.
Algumas pessoas possuem uma anomalia, denominada daltonismo, que impede a distin¸˜o de uma ou
ca
mais cores. O daltonismo se deve a um defeito na constitui¸˜o dos cones e est´ vinculada ao sexo. Ele
ca a
atinge cerca de 8% dos homens, e apenas 0.5% das mulheres. Esse defeito pode se manifestar em 1, 2 ou
nos 3 tipos de receptores. Os tricomatas s˜o daltˆnicos que possuem os 3 sistemas de pigmentos, mas que
a o
utilizam os sistemas em propor¸˜es diferentes das pessoas normais e das pessoas com o mesmo defeito. Os
co
dicromatas percebem as cores defeituosamente porque combinam apenas 2 sistemas. Os monocromatas
percebem apenas gradua¸˜es de claro e de escuro, pois sua estimula¸˜o visual se baseia em um unico
co ca ´
sistema crom´tico. Um outro aspecto que tamb´m influencia na percep¸˜o de cores ´ o amarelamento das
a e ca e
lentes do olho que ocorre com o passar dos anos, fazendo com que as pessoas se tornem menos sens´ ıveis,
por exemplo ` cor amarela do que ` cor azul.
a a
11.2 Sistemas de Cores Prim´rias
a
O conte´do desta se¸˜o, que descreve alguns sistemas de cores prim´rias, foi baseado principalmente em
u ca a
Hearn [Hea94], Cap´ ıtulo 15.
Um sistema de cores ´ um m´todo que explica as propriedades ou o comportamento das cores num
e e
contexto particular. N˜o existe um sistema que explique todos os aspectos relacionados ` cor. Por isso,
a a
s˜o utilizados sistemas diferentes para ajudar a descrever as diferentes caracter´
a ısticas da cor que s˜o a
percebidas pelo ser humano. Existem v´rios sistemas de cores, sendo que ser˜o apresentados apenas
a a
alguns dos principais: o XYZ, o RGB, o HSV e o HLS.
As cores prim´rias s˜o as 2 ou 3 cores que um sistema utiliza para produzir outras cores. As cores
a a
podem ser produzidas a partir de uma combina¸˜o das prim´rias, ou ent˜o, da composi¸˜o de 2 com-
ca a a ca
bina¸˜es. O universo de cores que podem ser reproduzidas por um sistema ´ chamado de espa¸o de cores
co e c
(color space ou color gamut). Alternativamente, um espa¸o de cores (color space) pode ser definido como
c
uma representa¸˜o visual de um modelo de cores, como o cubo definido pelas componentes do modelo
ca
RGB, ou o cone definido pelo modelo HSV. N˜o existe um conjunto finito de cores prim´rias que pro-
a a
duza todas as cores vis´ ıveis, mas sabe-se que uma grande parte delas pode ser produzida a partir de 3
prim´rias.
a
O estudo da utiliza¸˜o de 3 fontes de luz espectral para a gera¸˜o de cores ´ chamado de colorimetria, e
ca ca e
tem como um de seus objetivos determinar espa¸os de cor perceptualmente uniformes. Um espa¸o de cores
c c
(ou sistema de cores) perceptualmente uniforme ´ um no qual distˆncias perceptuais iguais separam todas
e a
as cores. Por exemplo, a escala de cinzas do espa¸o deve transmitir uma transi¸˜o suave entre o preto
c ca
e o branco. A defini¸˜o de um espa¸o de cores uniforme ´ feita atrav´s de medi¸˜es emp´
ca c e e co ıricas obtidas
sob condi¸˜es experimentais rigidamente controladas - as condi¸˜es do ambiente e outros parˆmetros
co co a
importantes devem ser mantidos constantes, como o tamanho das amostras de cores, o espa¸amento c
entre as amostras, a luminˆncia e cromaticidade do fundo e da luz ambiente. Apesar dessa limita¸˜o,
a ca
os espa¸os perceptuais de cores fornecem ferramentas adequadas para a solu¸˜o de problemas como a
c ca
compress˜o de imagens (para decidir o n´
a ıvel de codifica¸˜o da informa¸˜o de cor) e pseudo-colora¸˜o1
ca ca ca
(para mapear as cores da imagem em um conjunto com espa¸amento perceptual m´ximo).
c a
Os sistemas de cores podem ser aditivos ou subtrativos. Nos modelos aditivos (por exemplo, RGB
e XYZ), as intensidades das cores prim´rias s˜o adicionadas para produzir outras cores. A Figura 11.2
a a
ilustra a demonstra¸˜o do funcionamento desses modelos atrav´s da sobreposi¸˜o de c´
ca e ca ırculos coloridos.
Pode-se pensar que o branco ´ a mistura das intensidades m´ximas das 3 cores prim´rias aditivas
e a a
(vermelha, verde e azul). Os matizes intermedi´rios (amarelo, turquesa e magenta) s˜o obtidos atrav´s
a a e
da combina¸˜o das intensidades m´ximas de 2 cores.
ca a
Nos modelos subtrativos (por exemplo, o CMY), as cores s˜o geradas subtraindo-se o comprimento da
a
onda dominante da luz branca, por isso, a cor resultante corresponde ` luz que ´ refletida. A Figura 11.3
a e
ilustra a demonstra¸˜o do funcionamento desses modelos atrav´s da sobreposi¸˜o de c´
ca e ca ırculos coloridos.
Pode-se pensar que o preto ´ a combina¸˜o das 3 cores subtrativas (turquesa, magenta e amarela).
e ca
A quantidade de preto numa cor ´ indicada pela diferen¸a entre o branco e a intensidade m´xima das 3
e c a
cores prim´rias aditivas. E, da mesma forma, a quantidade de branco numa cor ´ indicada pela diferen¸a
a e c
entre o preto e a intensidade m´ ınima das 3 cores prim´rias aditivas.
a
1 A colora¸˜o “falsa” (“pseudocoloring”) ocorre quando as cores “verdadeiras” de uma imagem s˜o mapeadas em outro
ca a
conjunto de cores, ou quando uma imagem adquirida em tons de cinza ´ colorida.
e
96

98. Figura 11.2: Ilustra¸˜o da mistura de cores aditivas [For94].
ca
Figura 11.3: Ilustra¸˜o da mistura de cores subtrativas [For94].
ca
As cores puras e saturadas n˜o representam toda a classe de cores poss´
a ıveis, existem ainda os tints,
shades e tones que correspondem, respectivamente, `s cores obtidas atrav´s da adi¸˜o de branco, preto e
a e ca
cinza `s cores saturadas, causando uma altera¸˜o no efeito da cor. A Figura 11.42 ilustra de tints, shades
a ca
e tones obtidos a partir da cor vermelha.
Figura 11.4: Ilustra¸˜o da obten¸˜o de tints, shades e tones.
ca ca
A adi¸˜o de branco clareia uma cor e cria um tint (por exemplo, adicionando branco ao vermelho
ca
para obter a cor pink). A adi¸˜o de preto escurece uma cor e cria um shade (por exemplo, adicionando
ca
preto ao vermelho para obter um castanho-avermelhado (maroon). Al´m disso, a adi¸˜o de cinza reduz
e ca
o brilho de uma cor e cria um tone. Uma composi¸˜o monocrom´tica ´ formada inteiramente de tints,
ca a e
shades e tones da mesma cor.
11.3 Modelo XYZ
O sistema XY Z de cores prim´rias da CIE (Comiss˜o Internacional de Ilumina¸˜o) ´ um sistema aditivo
a a ca e
que descreve as cores atrav´s de 3 cores prim´rias virtuais X, Y e Z. Esse sistema foi criado devido `
e a a
inexistˆncia de um conjunto finito de cores prim´rias que produza todas as cores vis´
e a ıveis poss´
ıveis. Nesse
sistema, as cores Cl podem ser expressas pela seguinte equa¸˜o:
ca
Cl = x.X + y.Y + z.Z (11.1)
2 reproduzida de http://www.contrib andrew.cmu.edu:8001/usr/dw4e/color/tints.html.
97

99. em que X, Y e Z especificam as quantidades das prim´rias padr˜es necess´rias para descrever uma
a o a
cor espectral. A normaliza¸˜o dessa quantidade em rela¸˜o ` luminˆncia (X + Y + Z) possibilita a
ca ca a a
caracteriza¸˜o de qualquer cor. As cores desse sistema podem ser expressas como combina¸˜es das
ca co
quantidades normalizadas abaixo:
X Y Z
x= y= z= (11.2)
X +Y +Z X +Y +Z X +Y +Z
com x + y + z = 1. Assim, qualquer cor pode ser definida apenas pelas quantidades de x e y
que, por dependerem apenas do matiz e da satura¸˜o, s˜o chamadas de coordenadas de cromaticidade.
ca a
A descri¸˜o completa de uma cor ´ dada pelas coordenadas de cromaticidade e pelo valor de um dos 3
ca e
est´
ımulos originais, normalmente do Y , que cont´m a informa¸˜o de luminˆncia. Essa descri¸˜o possibilita
e ca a ca
a obten¸˜o das quantidades de X e Z com as equa¸˜es abaixo:
ca co
x z
X= Y Z= Y (11.3)
y y
onde z = 1 − x − y.
O sistema XYZ ´ formado por cores imagin´rias que s˜o definidas matematicamente. Nesse sistema, as
e a a
combina¸˜es de valores negativos e outros problemas relacionados ` sele¸˜o de um conjunto de prim´rias
co a ca a
reais s˜o eliminados. As coordenadas de cromaticidade x e y permitem representar todas as cores num
a
gr´fico bidimensional. O tra¸ado dos valores normalizados de x e y para as cores no espectro vis´
a c ıvel
resulta na curva ilustrada na Figura 11.5.
Figura 11.5: Diagrama de cromaticidade do CIE [Hea94].
Os pontos que representam as cores puras no espectro eletromagn´tico s˜o rotulados de acordo com os
e a
seus comprimentos de onda e est˜o localizados ao longo da curva que vai da extremidade correspondente
a
a
` cor vermelha at´ a extremidade correspondente ` cor violeta. A linha reta que une os pontos espectrais
e a
vermelho e violeta ´ chamada linha p´rpura, e n˜o faz parte do espectro. Os pontos internos correspondem
e u a
a todas as combina¸˜es poss´
co ıveis de cores vis´
ıveis, e o ponto C corresponde ` posi¸˜o da luz branca.
a ca
Devido ` normaliza¸˜o, o diagrama de cromaticidade n˜o representa os valores de luminˆncia. Por isso,
a ca a a
as cores com luminˆncias diferentes e cromaticidades iguais s˜o mapeadas no mesmo ponto. Atrav´s desse
a a e
diagrama, ´ poss´
e ıvel determinar e comparar os espa¸os de cores dos diferentes conjuntos de prim´rias,
c a
identificar as cores complementares (2 cores que, somadas, produzem a cor branca) e determinar o
comprimento de onda dominante e a satura¸˜o de uma cor.
ca
Os espa¸os de cor s˜o representados no diagrama, ilustrado na Figura 11.6a, atrav´s de linhas retas
c a e
ou de pol´ıgonos. Todas as cores ao longo da linha que une os pontos C1 e C2 na Figura 11.6a podem
ser obtidas atrav´s da mistura de quantidades apropriadas das cores correspondentes a esses pontos. A
e
escala de cores para 3 pontos (por exemplo, C3 , C4 e C5 na Figura 11.6a) ´ representada por um triˆngulo
e a
cujos v´rtices s˜o definidos pelas cores correspondentes `s 3 posi¸˜es e inclui cores contidas no interior e
e a a co
nas margens fronteiri¸as desse triˆngulo.
c a
Observando o diagrama ´ poss´ perceber que nenhum conjunto formado por 3 prim´rias pode gerar
e ıvel a
todas as cores, pois nenhum triˆngulo contido no diagrama abrange todas as cores poss´
a ıveis. As cores
complementares s˜o identificadas por 2 pontos localizados em lados opostos do ponto C e conectados por
a
uma linha reta. Por exemplo, misturando quantidades apropriadas de 2 cores C1 e C2 (Figura 11.6b),
obt´m-se a luz branca.
e
98

100. Figura 11.6: Representa¸˜o de escalas de cor no diagrama de cromaticidade do CIE [Hea94].
ca
A determina¸˜o do comprimento de onda dominante de uma cor pode ser feita interpretando-se
ca
a escala de cores entre 2 prim´rias. O comprimento de onda dominante da cor C1 , representada na
a
Figura 11.6c, ´ determinado tra¸ando-se uma linha reta que parte do ponto C passando pelo ponto C1 e
e c
intersectando a curva espectral no ponto Cs . A cor C1 , corresponde ent˜o, ` combina¸˜o da luz branca
a a ca
com a cor espectral Cs , pois Cs ´ o comprimento de onda dominante de C1 . O comprimento de onda
e
dominante das cores que est˜o entre o ponto C e a linha p´rpura ´ determinado de outra forma. Tra¸a-se
a u e c
uma linha a partir do ponto C (Figura 11.6c) passando pelo ponto C2 e intersectando a linha p´rpurau
no ponto Cp . Como esse ponto n˜o pertence ao espectro vis´
a ıvel, o ponto C2 ´ referenciado como sendo
e
uma cor n˜o espectral e o seu comprimento de onda dominante ´ obtido atrav´s do prolongamento da
a e e
reta at´ que ela intercepte a curva espectral, no ponto Csp . As cores n˜o espectrais est˜o entre p´rpura
e a a u
e magenta, e s˜o geradas atrav´s da subtra¸˜o do comprimento da onda dominante (como, por exemplo,
a e ca
o Csp ) da luz branca.
A pureza de uma cor (por exemplo, de C1 na figura 11.6c) ´ determinada atrav´s da distˆncia relativa
e e a
do ponto C1 , que corresponde ` linha reta que vai do ponto C at´ o ponto Cs . Pode-se calcular a pureza
a e
do ponto C1 atrav´s da rela¸˜o dc1 , onde dc1 representa a distˆncia entre C e C1 e dcs representa a
e ca dcs a
1
distˆncia entre C e Cs . A cor C1 ´ cerca de 25% pura porque est´ situada a aproximadamente 4 da
a e a
distˆncia total entre C e Cs .
a
11.4 Modelo RGB (Red, Green, Blue)
O sistema RGB de cores prim´rias tamb´m ´ aditivo e est´ baseado na teoria dos 3 est´
a e e a ımulos (Tristimulus
Color Theory) proposta por Young-Helmholtz e discutida na se¸˜o 2.3. Segundo essa teoria, o olho
ca
humano percebe a cor atrav´s da estimula¸˜o dos 3 pigmentos visuais presentes nos cones da retina, que
e ca
possuem picos de sensibilidade aproximada nos seguintes comprimentos de onda: 630 nm (Vermelho-
Red ), 530 nm (Verde-Green) e 450 nm (Azul-Blue). Esse sistema pode ser representado graficamente
atrav´s do cubo unit´rio definido sobre os eixos R, G e B, como ilustrado na Figura 11.7.
e a
A origem representa a cor preta, o v´rtice de coordenadas (1, 1, 1) representa a cor branca, os v´rtices
e e
que est˜o sobre os eixos representam as cores prim´rias e os demais v´rtices representam o complemento
a a e
de cada cor prim´ria. Cada ponto no interior do cubo corresponde a uma cor que pode ser representada
a
pela tripla (R, G, B), com os valores R, G e B variando de 0 a 1. Os tons de cinza s˜o representados ao
a
longo da diagonal principal do cubo, que vai da origem (ponto correspondente a cor preta) at´ o v´rtice
e e
que corresponde ` cor branca. Cada tom ao longo dessa diagonal ´ formado por contribui¸˜es iguais de
a e co
cada prim´ria. Logo, um tom de cinza m´dio entre o branco e o preto ´ representado por (0.5, 0.5, 0.5).
a e e
As cores Cl desse sistema podem ser expressas na forma:
Cl = r.R + g.G + b.B (11.4)
A resposta do olho aos est´
ımulos espectrais n˜o ´ linear e, por isso, algumas cores n˜o podem ser
a e a
reproduzidas pela sobreposi¸˜o das 3 prim´rias. Isso significa que algumas cores existentes na natureza
ca a
n˜o podem ser mostradas nesse sistema. Por isso, um fenˆmeno natural colorido como, por exemplo, de
a o
forma¸˜o de rochas, n˜o pode ser reproduzido com precis˜o (conforme discutido em Wolf [Wol93]).
ca a a
99

101. Figura 11.7: Cubo do RGB [Fol96].
11.5 Modelo HSV (Hue, Saturation, Value)
O sistema HSV utiliza descri¸˜es de cor que s˜o mais intuitivas do que combina¸˜es de um conjunto
co a co
de cores prim´rias e, por isso, ´ mais adequado para ser usado na especifica¸˜o de cores em n´
a e ca ıvel de
interface com o usu´rio. A cor ´ especificada atrav´s de uma cor espectral e das quantidades de branco e
a e e
preto que ser˜o adicionadas para a obten¸˜o de shades, tints e tones diferentes. A representa¸˜o gr´fica
a ca ca a
tridimensional do sistema HSV ´ um cone de 6 lados derivado do cubo RGB, mostrado na figura 11.8.
e
Figura 11.8: Cone hexagonal do HSV [Fol96].
Os parˆmetros de cor utilizados nesse sistema s˜o o matiz (hue), a satura¸˜o (saturation) e a lu-
a a ca
minˆncia (value). Os v´rios matizes est˜o representados na parte superior do cone, a satura¸˜o ´ medida
a a a ca e
ao longo do eixo horizontal e a luminˆncia ´ medida ao longo do eixo vertical, que passa pelo centro do
a e
cone. O matiz, que corresponde `s arestas ao redor do eixo vertical, varia de 0◦ (vermelho) a 360◦ , e o
a
ˆngulo entre os v´rtices ´ de 60◦ . A satura¸˜o varia de 0 a 1 e ´ representada como sendo a raz˜o entre
a e e ca e a
a pureza de um determinado matiz e a sua pureza m´xima (S = 1). Um determinado matiz possui 1
a 4
de pureza em S = 0.25. Quando S = 0 tem-se a escala de cinzas. A luminˆncia varia de 0 (no pico do
a
cone), que representa a cor preta, a 1 (na base), onde as intensidades das cores s˜o m´ximas.
a a
11.6 Modelo HLS (Hue, Lightness, Saturation)
O sistema HLS3 tamb´m ´ baseado em parˆmetros mais intuitivos para a descri¸˜o de cores.
e e a ca
A representa¸˜o gr´fica tridimensional desse sistema ´ um cone duplo, como mostra a figura 9. Os 3
ca a e
parˆmetros de cor utilizados s˜o o matiz (hue), a luminosidade (lightness 4 ) e a satura¸˜o (saturation).
a a ca
3 Outros autores denominam esse sistema como Hue, Luminance, Saturation [Rog93a].
4 Luminosidade (lightness): Segundo Foley [Fol96], esse termo est´ relacionado ` no¸˜o acrom´tica da intensidade per-
a a ca a
cebida de um objeto que reflete luz. Brilho (brightness) ´ usado no lugar de luminosidade para denotar a intensidade
e
percebida de um objeto que emite luz.
100

102. Figura 11.9: Cone duplo do HLS [Fol96].
O ˆngulo em rela¸˜o ao eixo vertical varia de 0◦ (matiz azul) a 360◦ em intervalos de 60◦ e especifica
a ca
um matiz. O eixo vertical corresponde ` luminosidade e varia de 0 (preto) a 1 (branco) e ´ onde se
a e
encontra a escala de cinzas. A satura¸˜o varia de 0 a 1, e os matizes puros s˜o encontrados no plano
ca a
onde a luminosidade ´ igual a 0.5 e a satura¸˜o ´ igual a 1. Quanto menor o valor da satura¸˜o menor ´
e ca e ca e
a pureza do matiz; e quando a satura¸ao ´ igual a 0, tem-se a escala de cinzas.
c˜ e
Os sistemas HLS e HSV permitem que se pense em termos de cores mais “claras” e mais “escuras”. As
cores s˜o especificadas atrav´s de um ˆngulo, e os diversos shades, tints, e tones de cada cor s˜o obtidos
a e a a
atrav´s do ajuste do brilho ou luminosidade e da satura¸˜o. As cores mais claras s˜o obtidas atrav´s do
e ca a e
aumento do brilho ou da luminosidade e as cores mais escuras pela diminui¸˜o dos mesmos. As cores
ca
intermedi´rias s˜o obtidas atrav´s da diminui¸˜o da satura¸˜o.
a a e ca ca
101

103. Cap´
ıtulo 12
Processamento Digital de Imagens
12.1 Introdu¸˜o
ca
A ´rea de Processamento Digital de Imagens tem crescido consideravelmente nas ultimas duas d´cadas,
a ´ e
com a utiliza¸˜o de imagens e gr´ficos em uma grande variedade de aplica¸˜es, aliado ao fato de que
ca a co
a tecnologia de constru¸˜o de computadores tamb´m tem se aprimorado, possibilitando a utiliza¸˜o de
ca e ca
sistemas mais eficientes e mais baratos. Muitas ´reas vˆm utilizando Sistemas de Processamento Digital
a e
de Imagens, tais como: reconhecimento de padr˜es (ind´stria), medicina, agricultura, pesquisas espaciais,
o u
meteorologia, etc.
12.2 Considera¸˜es Sobre Imagens
co
Uma imagem cont´
ınua, ´ digitalizada atrav´s de dois processos:
e e
• Amostragem (Sampling): digitaliza¸˜o em termos espaciais (tamanho da grade de digitaliza¸˜o);
ca ca
• Quantiza¸˜o: digitaliza¸˜o em termos de amplitude (no de n´
ca ca ıveis de cinza).
A Figura 12.1, ilustra o processo de quantiza¸˜o, para v´rios tamanhos de grade. A Figura ??,
ca a
apresenta uma imagem de 512x512 pixels, quantizada de v´rias formas.
a
Matematicamente, Imagem Digital pode ser definida como uma fun¸˜o bidimensional A(x, y) definida
ca
em uma certa regi˜o do plano.
a
A : [0, r] × [0, s] → [0, t] (12.1)
Assim a imagem ´ definida num retˆngulo [0, r]×[0, s], e os valores tomados est˜o contidos no intervalo
e a a
[0, t]. Ao valor A(x, y) no ponto (x, y) d´-se o nome de N´ de cinza.
a ıvel
Imagens s˜o geralmente definidas como uma grande cole¸˜o de dados, que est˜o frequentemente
a ca a
dispostos em forma de uma matriz ou alguma outra estrutura de dados discreta.
Uma imagem, ´ representada atrav´s de um conjunto de valores, onde cada valor ´ um n´mero que
e e e u
descreve os atributos de um pixel na imagem. Usualmente estes n´meros s˜o inteiros positivos, que
u a
representam a intensidade na escala de tons de cinza de um ponto da imagem, ou a cor associada ao
ponto pela “look-up table”, em sistemas que comportam este procedimento. Quando utiliza-se escalas de
tons de cinza, usualmente associa-se a tonalidade de cinza mais escura, o preto, ao n´ zero da escala de
ıvel
cinza, e o mais claro, o branco, ao maior valor permitido na escala. Ou seja, se cada pixel ´ representado
e
em um sistema de 8-bits, o preto ´ associado ao valor zero, e o branco ao valor 255.
e
As dimens˜es do conjunto de valores que especifica a imagem s˜o chamadas de largura e altura da
o a
imagem, e o n´mero de bits associado com cada pixel da matriz ´ chamado de profundidade da imagem.
u e
A profundidade da imagem est´ associada ao n´mero de planos de mem´ria em que uma imagem ´
a u o e
mapeada, sendo que cada bit da palavra que armazena o valor do pixel reside em um plano da imagem
(“frame buffer”). Na Figura 12.3 mostra-se um esquema de um pixel p com profundidade 8.
Atrav´s de Processamento Digital de Imagens, pode-se analisar e modificar imagens por computador.
e
Os objetivos deste processamento s˜o: a
1. Extrair informa¸˜o da imagem, ou seja, reconhecer elementos que comp˜em a imagem, permitir
ca o
medir elementos contidos na imagem, classific´-los e compar´-los com algum modelo colocado.
a a
102

104. Figura 12.1: Efeitos sobre uma imagem, de se reduzir o tamanho da grade de amostragem.
2. Transformar a imagem (aumentando contraste, real¸ando bordas, corrigindo alguma imperfei¸˜o
c ca
gerada na imagem durante o processo de aquisi¸˜o), de forma que a informa¸˜o seja mais facilmente
ca ca
discern´ por um analista humano.
ıvel
12.3 Tabelas “Look-up”
Em sistemas que permitem trabalhar com cores, cada cor ´ uma composi¸˜o de trˆs cores prim´rias:
e ca e a
vermelho, verde e azul (do inglˆs, RGB). E os n´
e ıveis de cinza tamb´m s˜o uma composi¸˜o das trˆs
e a ca e
cores, sendo que todas entram em partes iguais. Logo, o n´mero de bits utilizados para representar o
u
valor do pixel ´ dividido entre as trˆs cores. Assim, se um pixel possui profundidade 1 (um bit por pixel),
e e
o pixel poder´ ser pintado apenas com duas cores (21 ) (por exemplo, em preto e branco). Se o pixel
a
utiliza dois bits, poder´ produzir no m´ximo quatro cores (22 ), e assim por diante. Usualmente 6 bits s˜o
a a a
suficientes para permitir a visualiza¸˜o da imagem de forma que n˜o se perceba descontinuidade entre
ca a
as tonalidades de cinza, mas 8 ou mais bits podem ser necess´rios em algumas aplica¸˜es. Assim, para
a co
monitores coloridos, sugere-se que trˆs vezes a quantidade de bits necess´ria ´ um bom valor, ou seja, 8
e a e
bits para cada cor prim´ria aditiva (vermelha, verde e azul - RGB), produzindo 24 bits por pixel.
a
Em muitos sistemas gr´ficos ´ desej´vel poder-se alterar rapidamente a colora¸˜o da imagem sem
a e a ca
alterar a sua forma. Assim permite-se alterar a aparˆncia visual de uma imagem, sem na realidade
e
alterar os pr´prios dados que a definem. Por exemplo, mostrar todos os pixels abaixo de um certo valor
o
com o preto, ou mesmo a partir de uma imagem monocrom´tica criar uma imagem em pseudo-cor.
a
Um dispositivo que facilita grandemente essa manipula¸˜o com cores, sem comprometer a eficiˆncia
ca e
da opera¸˜o de visualiza¸˜o de imagens s˜o as tabelas de Busca (“Look-up Table” - LUT), que os
ca ca a
controladores de monitores por varredura vem utilizando. A tabela “look-up” possui tantas entradas
quanto o n´mero de valores armazenados pelo pixel, ou seja, se o pixel tem profundidade 8, a LUT ter´
u a
256 (28 ) entradas. Assim, o valor do pixel n˜o indica a cor em que ele ´ mapeado, mas sim a entrada
a e
na LUT onde a cor est´ armazenada. A Figura 12.4 ilustra o procedimento de mapeamento de um pixel
a
atrav´s da LUT.
e
12.4 Tipos de Manipula¸˜o de Imagens
ca
Na an´lise de imagens, a entrada do processamento ´ uma imagem, enquanto a sa´ ´ uma descri¸˜o n˜o
a e ıda e ca a
pict´rica da imagem. Este processo pode ser entendido como de “redu¸˜o de dados”, em que se diminui
o ca
103

105. Figura 12.2: Uma imagem de 512 x 512 pixels, quantizada em (a) 256 n´ ıveis, (b) 128 n´
ıveis, (c) 64 n´
ıveis,
(d) 32 n´
ıveis, (e) 16 n´
ıveis, (f) 8 n´
ıveis, (g) 4 n´
ıveis e (h) 2 n´
ıveis de cinza.
Figura 12.3: Representa¸˜o de um pixel P com 8-bits (8 planos) de profundidade.
ca
o volume dos dados, mas mant´m-se o conte´do da informa¸˜o relevante para uma dada aplica¸˜o.
e u ca ca
Na manipula¸˜o de imagens em geral, tanto as entradas quanto as sa´
ca ıdas s˜o imagens. Duas grandes
a
classes de transforma¸˜es s˜o:
co a
• Transforma¸˜es Radiom´tricas: onde os valores de n´
co e ıveis de cinza dos pontos da imagem s˜o
a
alterados, sem modifica¸˜o de sua geometria.
ca
• Transforma¸˜es Geom´tricas: onde a geometria da imagem ´ alterada, mantendo-se o m´ximo
co e e a
poss´ os valores dos n´
ıvel ıveis de cinza.
As transforma¸˜es radiom´tricas e geom´tricas podem ser feitas com a finalidade de eliminar distor¸˜es
co e e co
da imagem, introduzidas geralmente pelo pr´prio sistema de aquisi¸˜o de imagens (“restaura¸˜o”), ou
o ca ca
enfatizar certas caracter´
ısticas da imagem (“realce”).
12.5 Transforma¸˜es Radiom´tricas
co e
Pode-se ter basicamente dois tipos de transforma¸˜es ou opera¸˜es radiom´tricas:
co co e
• Restaura¸˜o - que visa corrigir alguma distor¸˜o sofrida pela imagem;
ca ca
• Realce - que procura enfatizar alguma caracter´
ıstica de interesse da imagem. Por vezes estes dois
objetivos produzem resultados coincidentes.
´
E o caso, por exemplo, quando uma imagem sofreu uma distor¸˜o que diminuiu seu contraste; uma
ca
transforma¸˜o que realce as bordas dos objetos das imagens pode, de fato, restaur´-la.
ca a
Embora muitas da t´cnicas de restaura¸˜o e realce sejam as mesmas (por exemplo, filtragem), os
e ca
objetivos e enfoques divergem num e noutro caso. O procedimento geral da restaura¸˜o ´ a modelagem
ca e
do processo de distor¸˜o para tentar invertˆ-lo. No realce esta preocupa¸˜o n˜o existe, pois no realce as
ca e ca a
t´cnicas utilizadas s˜o, na maioria, heur´
e a ısticas, n˜o havendo compromisso com a imagem original.
a
As transforma¸˜es radiom´tricas podem tamb´m ser classificadas quanto ao seu grau de abrangˆncia,
co e e e
em:
104

106. Figura 12.4: Organiza¸˜o de uma LUT, para um sistema de pixels de 8 bits.
ca
1. Opera¸˜es Pontuais: onde o n´
co ıvel de cinza de um ponto na imagem transformada depende s´ o
do n´
ıvel de cinza do ponto da imagem original (ou nas imagens originais se houver mais de uma
imagem de entrada (“frames”)).
2. Opera¸˜es Locais: onde o novo n´ de cinza de um ponto depende n˜o s´ de seu antigo n´
co ıvel a o ıvel
de cinza, mas tamb´m dos n´
e ıveis de cinza de seus pontos vizinhos.
12.5.1 Opera¸˜es Pontuais sobre Imagens
co
Algoritmos que realizam Opera¸˜es Pontuais percorrem a imagem e utilizam o valor do pixel associado
co
a cada ponto, modificando a escala de tonalidades de cinza de uma imagem. Por exemplo caso deseja-se
tornar uma imagem mais brilhante, pode-se adicionar algum valor a todos os pontos da imagem. Por
exemplo, em um sistema de 8-bits por pixel, os valores associados v˜o de 0 a 255, pode-se definir uma
a
fun¸˜o brilho(p) = p + 40, cuja fun¸˜o ´ tornar a imagem mais “clara”. Atrav´s de opera¸˜es pontuais
ca ca e e co
pode-se tamb´m corrigir sombras que porventura tenham surgido junto com o processo de aquisi¸˜o da
e ca
imagem. Ou seja, define-se uma fun¸˜o cujo efeito reverta a opera¸˜o de sombreamento indesej´vel,
ca ca a
por´m isto requer que se estime as fun¸˜es de sombreamento.
e co
Assim, uma opera¸˜o pontual que toma uma imagem A(x, y) e produz outra imagem B(x, y), pode
ca
ser definida matematicamente como:
B(x, y) = f [A(x, y)] (12.2)
Histogramas de Intensidades
O Histograma de Intensidades indica para cada n´ ıvel de cinza da imagem a quantidade de pontos
mapeados com tal n´ ıvel. Ele cont´m uma informa¸˜o global sobre os “objetos” da imagem. Se todos os
e ca
pontos da imagem s˜o de um mesmo objeto, o histograma mostra a probabilidade condicional p(z/objeto)
a
de um ponto possuir um dado n´ ıvel de cinza z, sendo que o ponto pertence ao objeto. A Figura 12.5
apresenta uma imagem e seu histograma de intensidades associado.
Atrav´s de Histogramas de Intensidades pode-se obter uma maneira simples para se manipular o
e
contraste de imagens. Dessa forma, pode-se definir as “janelas” de intensidade que se queira manipular.
Por exemplo, se ao construir o histograma de uma imagem vˆ-se que n˜o se est´ utilizando toda a
e a a
abrangˆncia dos n´
e ıveis de cinza, resultando uma imagem com pouco contraste, pode-se for¸ar que ela seja
c
mapeada usando todos os n´ ıveis de cinza, ou uma faixa deles (“janela”), ou mesmo aumentar o contraste
em apenas uma regi˜o dos n´
a ıveis de intensidade da imagem [Gonzalez and Wintz, 1987].
Suponha-se uma imagem A(x, y) e seu histograma H1 (A). Se um ponto p da imagem est´ mapeado a
com o n´ N dentro da faixa de valores ∆1 , cujo n´ mais baixo ´ min1 e o mais alto ´ max1 , e atrav´s
ıvel ıvel e e e
de manipula¸˜o no histograma deseja-se transform´-lo para o valor p com n´ N , o qual estar´ dentro
ca a ıvel a
da faixa ∆2 cujo valor m´ ınimo ´ min2 e m´ximo max2 , a fun¸˜o de transforma¸˜o ser´:
e a ca ca a
(N − min1 )(max2 − min2 )
f (N ) = + min2 (12.3)
(max1 − min1 )
N = f (N ) (12.4)
A Figura 12.6 ilustra a transforma¸ao do histograma H1 (A) da imagem A para o histograma H2 (A).
c˜
105

107. Figura 12.5: Imagens e histogramas de intensidade.
Esse procedimento de manipula¸˜o do histograma para ampliar ou diminuir o contraste de uma
ca
imagem ´ mostrado na Figura 12.7. Na parte (a) apresenta-se um histograma de uma imagem, na
e
qual especifica-se uma janela de visualiza¸˜o, e na parte (b) o histograma da mesma imagem depois da
ca
manipula¸˜o do histograma.
ca
Opera¸˜es Alg´bricas
co e
Por defini¸˜o, opera¸˜es Alg´bricas, s˜o aquelas que produzem uma imagem que ´ a soma, diferen¸a,
ca co e a e c
produto ou quociente pixel a pixel de suas imagens. No caso de soma ou multiplica¸˜o mais de duas
ca
imagens podem estar envolvidas.
As quatro opera¸˜es alg´bricas de processamento de imagens podem ser explicitadas:
co e
C(x, y) = A(x, y) + B(x, y) (12.5)
C(x, y) = A(x, y) − B(x, y) (12.6)
C(x, y) = A(x, y) × B(x, y) (12.7)
C(x, y) = A(x, y)/B(x, y) (12.8)
onde: A(x, y) e B(x, y) s˜o imagens de entrada e C(x, y) ´ a imagem resultante.
a e
A seguir s˜o apresentadas algumas aplica¸˜es imediatas para as opera¸˜es alg´bricas:
a co co e
1. Uma importante utiliza¸˜o de adi¸˜o de imagens, ´ para se obter a m´dia de m´ltiplas imagens de
ca ca e e u
uma mesma cena. Isto ´ eficazmente utilizado para reduzir os efeitos de ru´
e ıdos aleat´rios aditivos.
o
Pode tamb´m ser utilizado para colocar o conte´do de uma imagem sobrepondo outra.
e u
2. Subtra¸˜o de imagens pode ser utilizada para remover algum padr˜o indesej´vel presente em uma
ca a a
imagem. A subtra¸˜o ´ tamb´m utilizada para detectar mudan¸as entre duas imagens da mesma
ca e e c
cena. Por exemplo, pode-se detectar movimento subtraindo-se imagens sequenciais de uma cena.
Subtra¸˜o de imagens pode ser usada para calcular o gradiente, uma fun¸˜o muito usada para
ca ca
detec¸˜o de bordas (ver se¸˜o 2.4.2.2?). Uma utiliza¸˜o t´
ca ca ca ıpica em medicina, ´ para se comparar
e
duas imagens de uma mesma regi˜o do corpo. Obt´m-se a imagem da regi˜o (ou ´rg˜o) normal e
a e a o a
tamb´m ap´s injetar um meio de contraste, adquire outra imagem. Ap´s esta opera¸˜o, pode-se
e o o ca
comparar as duas atrav´s de subtra¸˜o digital. Assim, por exemplo, se o cora¸˜o ´ o ´rg˜o em
e ca ca e o a
aprecia¸˜o, consegue-se obter uma imagem apenas das art´rias e veias.
ca e
3. Multiplica¸˜o e divis˜o de imagens podem ser utilizadas, por exemplo, para corrigir poss´
ca a ıveis defeitos
de um digitalizador em que a sensibilidade do sensor de luz varia conforme a posi¸˜o dos pontos
ca
da imagem. Multiplicar uma imagem por uma “m´scara” pode esconder certas regi˜es da imagem
a o
deixando expostos apenas objetos de interesse.
106

108. Figura 12.6: Efeito de uma transforma¸˜o dos n´
ca ıveis de cinza efetuado sobre o histograma.
Figura 12.7: Manipula¸˜o de janelas de intensidade da imagem atrav´s do histograma.
ca e
Ao se efetuar opera¸˜es sobre as imagens, deve-se estar atento para que o novo valor obtido n˜o
co a
ultrapasse o dom´ınio de valores, permitido pela amplitude dos n´ıveis de intensidade em que a imagem
est´ mapeada. Se este cuidado n˜o for tomado, pode-se obter valores totalmente inconsistentes, levando-se
a a
a uma degenera¸˜o da imagem.
ca
12.5.2 Opera¸˜es Locais Sobre a Imagem
co
Algor´ıtmos que realizam Opera¸˜es Locais utilizam informa¸˜o dos valores dos pontos vizinhos para
co ca
modificar o valor de um ponto, ou mesmo para verificar a existˆncia de alguma propriedade neste ponto
e
da imagem.
Opera¸˜es Locais s˜o tipicamente utilizadas para filtragem espacial e altera¸˜o da pr´pria estrutura
co a ca o
da imagem. Elas podem “agu¸ar” a imagem, acentuando as mudan¸as de intensidades (atrav´s de filtros
c c e
Passa-Altas), ou “suavizar” a imagem, tornando as mudan¸as de intensidade menos abruptas (atrav´s de
c e
filtros Passa-Baixas), ou podem prover outras formas de se melhorar a imagem. Assim, pode-se procurar
formas na imagem atrav´s de “padr˜es de busca” (“match”), obter medidas dos elementos da imagem,
e o
definir bordas na imagem, remover ru´ suavizando a imagem [?].
ıdo
As transforma¸˜es locais s˜o divididas em dois grandes grupos:
co a
• Transforma¸˜es Lineares: s˜o aquelas em que os pixels vizinhos ao que est´ sendo calculado
co a a
influenciam no novo valor segundo uma combina¸˜o linear dos mesmos. Tais opera¸˜es incluem
ca co
superposi¸˜o e convolu¸˜o de imagens, o que ´ usualmente utilizado para implementar filtros dis-
ca ca e
cretos.
• Transforma¸˜es n˜o Lineares: utilizam outra forma de arranjo que n˜o a linear.
co a a
107

109. Opera¸˜o de Convolu¸˜o
ca ca
Um dos algoritmos cl´ssicos de processamento de imagens ´ aquele que efetua a Convolu¸˜o entre
a e ca
imagens, sendo comumente usado para realizar filtragem espacial e procurar peculiaridades na imagem.
A opera¸˜o de convolu¸˜o substitui o valor de um ponto com o valor obtido atrav´s de uma opera¸˜o
ca ca e ca
linear do ponto e de seus vizinhos, sendo que ´ atribu´ “peso” aos vizinhos e ao ponto. Estes “pesos”
e ıdo
s˜o colocados em uma matriz, usualmente de dimens˜o pequena, chamada de m´scara. Se para obter um
a a a
novo valor de um ponto deseja-se que apenas os vizinhos imediatos influenciem, escolhe-se uma m´scara a
de dimens˜o 3x3, onde o ponto base para a gera¸˜o do novo ponto ´ colocado no centro da m´scara.
a ca e a
Dadas duas imagens A(x, y) e B(x, y), com x = 0, 1, ..., M − 1 e y = 0, 1, ...N − 1, a convolu¸˜o ca
(discreta) destas duas imagens ´ uma terceira imagem C(x, y) com x = 0, 1, ..., M − 1 e y = 0, 1, ..., N − 1,
e
dada pela seguinte express˜o:
a
M −1 N −1
1
C(x, y) = A(m, n).B(x − m, y − n) (12.9)
M.N m=0 n=0
e para os valores da borda da imagem, que se encontram fora dos intervalos [0, M − 1] e [0, N − 1], deve-se
utilizar as seguintes rela¸˜es:
co
A(x, −y) = A(x, N − y) (12.10)
A(−x, y) = A(M − x, y) (12.11)
As rela¸˜es acima s˜o equivalentes a considerar uma imagem A(x, y) definida em [0, M −1] e [0, N −1],
co a
como definida em [−M, M − 1] e [−N, N − 1]. O resultado da convolu¸˜o de A por B num ponto p ´ na
ca e
realidade uma m´dia ponderada dos pontos de A, onde os pesos s˜o dados pela imagem B.
e a
Como foi mencionado acima, a opera¸˜o de convolu¸˜o ´ a base para efetuar-se filtragem espacial
ca ca e
de imagens. A imagem que indica os pesos para a convolu¸˜o normalmente possui dimens˜o pequena e
ca a
´
ımpar (3, 5, 7 ou 9), pois a opera¸˜o de convolu¸˜o envolve uma grande quantidade de c´lculos, e quanto
ca ca a
maior o m´scara maior ser´ o tempo de processamento da opera¸˜o.
a a ca
A seguir ser˜o apresentadas algumas m´scaras normalmente utilizadas para filtragem espacial [Mascarenhas and Vel
a a
 
1/9 1/9 1/9
 1/9 1/9 1/9  (12.12)
1/9 1/9 1/9
Implementa um filtro passa-baixas (de suaviza¸˜o):
ca
 
0 −1 0
 −1 5 −1  (12.13)
0 −1 0
Normalmente utilizada para “agu¸ar” uma imagem, pois como alguns pesos s˜o negativos eles tendem
c a
a real¸ar diferen¸as.
c c
   
1 1 1 −1 −1 −1
(a)  1 −2 1  (b)  1 −2 1  (12.14)
−1 −1 −1 1 1 1
Apresenta uma m´scara de filtro para dete¸˜o de borda ao (a) norte e (b) ao sul do ponto.
a ca
   
−1 1 1 1 1 −1
(a)  −1 −2 1 (b)  1 −2 −1  (12.15)
−1 1 1 1 1 −1
Apresenta uma m´scara de filtro para dete¸˜o de borda a (a) leste e (b) a oeste do ponto.
a ca
O realce de bordas, independente da dire¸˜o pode ser obtido atrav´s de m´scaras como:
ca e a
     
0 −1 0 −1 −1 −1 1 −2 1
 −1 4 −1   −1 8 −1   −2 4 −2  (12.16)
0 −1 0 −1 −1 −1 1 −2 1
Pode-se tamb´m utilizar m´scaras que contenham algum padr˜o que se quer procurar na imagem.
e a a
Neste caso a m´scara ´ normalmente chamada de tentativa (“template”), onde o tamanho da m´scara
a e a
depende do padr˜o a ser procurado.
a
108

110. Exemplos de Transforma¸˜es n˜o Lineares
co a
Usualmente as transforma¸˜es n˜o lineares conseguem uma melhor rela¸˜o sinal/ru´ na imagem pro-
co a ca ıdo
duzida do que por transforma¸˜es lineares. Os filtros lineares utilizados para atenuar os ru´
co ıdos de uma
imagem (passa-baixas) produzem uma imagem “borrada”, ou seja as bordas n˜o ficam mais t˜o n´
a a ıtidas.
Este efeito indesejado pode ser minorado atrav´s de transforma¸˜es (filtros) n˜o lineares.
e co a
Figura 12.8: Sinais “ru´
ıdo” (a) e “degrau” (b).
Tome-se como exemplo os sinais unidimensionais dos tipos “ru´ ıdo” e “degrau” mostrados na Figura
12.9 [Mascarenhas and Velasco, 1989]. Os efeitos de uma transforma¸˜o linear (filtro) dos tipos m´dia
ca e
[1/3, 1/3, 1/3] e diferen¸a [−1, 3, −1] s˜o mostrados na Figura 12.9. Pode-se notar nestes casos os efeitos
c a
de atenua¸˜o do ru´ (a), “borramento” da borda (b), amplia¸˜o do ru´ (c) e realce da borda (d).
ca ıdo ca ıdo
Os efeitos indesejados mostrados na Figura 12.10 (c) e (d) podem ser minorados atrav´s de filtros n˜o
e a
lineares, como ser´ visto a seguir.
a
Figura 12.9: Sinais “ru´
ıdo” (a) e “degrau” (b).
Por exemplo, no filtro da mediana, os pontos da vizinhan¸a do ponto (x, y) s˜o ordenados, e tomado
c a
como novo valor para (x, y) o valor mediano obtido pela ordena¸˜o. O efeito do filtro da mediana
ca
(unidimensional) que envolve 3 elementos (o ponto e seus vizinhos mais pr´ximos) ´ mostrado na Figura
o e
109

111. Figura 12.10: Efeitos de filtros lineares ao “ru´ıdo” e ` “borda”: (a) efeitos de atenua¸˜o; (b) borramento
a ca
da borda; (c) amplia¸˜o do ru´
ca ıdo; (d) realce da borda.
12.11. Note-se que na parte (a) da figura o ru´ foi eliminado (n˜o somente atenuado), enquanto em (b)
ıdo a
o degrau permaneceu inalterado.
Figura 12.11: Efeito do filtro da mediana sobre o “ru´
ıdo” e o “degrau”.
´
E tamb´m usual, em vez de se utilizar a mediana da vizinhan¸a, escolher o valor m´ximo ou o valor de
e c a
ordem qualquer. Se a imagem ´ bin´ria, para se obter o valor m´
e a ınimo entre dois pontos, pode-se utilizar
a opera¸˜o l´gica E dos valores da vizinhan¸a dois a dois, e para o valor m´ximo a opera¸˜o l´gica OU.
ca o c a ca o
Uma outra alternativa utilizada ´ tomar-se o valor mais frequente de uma vizinhan¸a, ou seja, utilizar
e c
a Moda, entre eles.
Pode-se utilizar vizinhan¸a seletiva de um ponto, isto ´, tomar a m´dia n˜o em toda a vizinhan¸a,
c e e a c
mas sim numa sub-vizinhan¸a que satisfa¸a alguma propriedade dada, como uniformidade, ou seja, que
c c
apresente um valor m´dio pr´ximo do valor do ponto (x, y). O uso do filtro da vizinhan¸a seletiva presume
e o c
que a imagem seja composta de regi˜es razoavelmente uniformes. Assim, a sele¸˜o da vizinhan¸a procura
o ca c
fazer com que o ponto (x, y) seja operado s´ com pontos de sua regi˜o.
o a
Pode-se tamb´m utilizar filtros n˜o-lineares para detectar, bordas e linhas curvas. Para o realce
e a
de bordas o m´todo n˜o-Linear mais simples ´ o Operador Gradiente de Roberts (GR), dado por
e a e
[Mascarenhas and Velasco, 1989]:
1
2 2
GR(x, y) = [[A(x, y) − A(x − 1, y − 1)] + [A(x, y − 1) − A(x − 1, y)] ] 2 (12.17)
onde A(x, y) ´ a imagem dada.
e
110

112. Uma desvantagem do operador de Roberts ´ sua assimetria, pois, dependendo da dire¸˜o, certas
e ca
bordas s˜o mais real¸adas que outras, mesmo tendo igual magnitude.
a c
Um operador gradiente para delimita¸˜o de bordas mais sofisticado (3x3), ´ o Operador de Sobel
ca e
(GS), o qual ´ frequentemente utilizado como o primeiro passo para algoritmos de vis˜o computacional.
e a
Este operador ´ dado por:
e
1
GS(x, y) = (X 2 + Y 2 ) 2 (12.18)
onde:
X = [A(x − 1, y + 1) + 2.A(x, y + 1) + A(x + 1, y + 1)]−

[A(x − 1, y − 1) + 2A(x, y − 1) + A(x + 1, y − 1)]

(12.19)
Y
 = [A(x − 1, y − 1) + 2.A(x − 1, y) + A(x − 1, y + 1)]−
[A(x + 1, y + 1) + 2A(x + 1, y) + A(x + 1, y − 1)]
Transforma¸˜es Geom´tricas
co e
As transforma¸˜es geom´tricas mudam o arranjo espacial dos pixels da imagem. Muitas vezes s˜o uti-
co e a
lizadas para corrigir distor¸˜es causadas pelo processo de aquisi¸˜o, ou mesmo para efetuar alguma
co ca
manipula¸˜o solicitada pelo usu´rio. Tranforma¸˜es geom´tricas t´
ca a co e ıpicas s˜o: rota¸˜o, transla¸˜o, am-
a ca ca
plia¸˜o, ou diminui¸˜o da imagem. Algoritmos para efetuarem estas opera¸˜es podem ser apresentados
ca ca co
como um conjunto de equa¸˜es que mapeiam um pixel localizado na posi¸˜o (x, y) em um novo endere¸o,
co ca c
(x , y ).
Na realidade, em processamento digital de imagens, geralmente s˜o necess´rios dois algoritmos se-
a a
parados para a maior parte das transforma¸˜es geom´tricas. O primeiro ´ o algoritmo que define a
co e e
movimenta¸˜o dos pixels, como ele move a partir da posi¸˜o inicial para a posi¸˜o final.
ca ca ca
Figura 12.12: Uma transforma¸˜o geom´trica de 90o graus.
ca e
Como exemplo, pode-se tomar a imagem ilustrada na Figura 12.12. Ali uma imagem ´ rotacionada
e
de 90o graus. Um pixel na posi¸˜o (0,0) ´ mapeado segundo a f´rmula:
ca e o
x = (Y SIZE − 1) − y
y =x (12.20)
onde Y SIZE ´ o n´mero de pixels no eixo y.
e u
Em muitas aplica¸˜es, ´ necess´rio preservar a continuidade dos objetos que definem a imagem. Isso
co e a
pode ser feito transformando-se ponto a ponto a imagem, ou transformando-se apenas pontos chave da
imagem, fazendo que os outros pontos acompanhem a transforma¸˜o por algum outro processo. Pode-se
ca
ver que o primeiro processo ´ geralmente mais oneroso em termos de tempo de computa¸˜o do que o
e ca
segundo.
´
E conveniente especificar matematicamente o relacionamento espacial entre pontos das imagem de
entrada e da imagem de sa´ıda. A defini¸˜o geral para opera¸˜es geom´tricas ´ [Castleman, 1979]:
ca co e e
g(x, y) = f (x , y ) = f (a(x, y), b(x, y)) (12.21)
111

113. onde f (x, y) ´ a imagem de entrada e g(x, y) ´ a imagem de sa´
e e ıda. As fun¸˜es a(x, y) e b(x, y) especificam
co
as transforma¸˜es espaciais. Se essas tranforma¸˜es forem cont´
co co ınuas, a continuidade ser´ preservada na
a
nova imagem.
O segundo algoritmo necess´rio para uma transforma¸˜o geom´trica ´ um algoritmo para interpola¸˜o
a ca e e ca
dos valores dos n´ ıveis de cinza. Na imagem de entrada f (x, y), os valores do n´
ıveis de cinza s˜o definidos
a
somente para valores inteiros de x e y. Mas na equa¸˜o geral acima, pode-se ver que o valor do n´ de
ca ıvel
cinza para g(x, y) pode ser tomado a partir de coordenadas n˜o inteiras (pela continuidade) de f (x, y). Se
a
a opera¸˜o geom´trica ´ considerada como um mapeamento de f para g, pixels de f podem ser mapeados
ca e e
entre pixels de g e vice-versa. Assim novamente deve ser realizada alguma opera¸˜o (ex. escala) para
ca
corrigir a distor¸˜o de pontos n˜o inteiros.
ca a
112

114. Referˆncias Bibliogr´ficas
e a
[Castleman, 1979] Castleman, K. R. (1979). Digital Image Processing. Prentice-Hall, Inc., Englewood
Cliffs, N.J.
[Gonzalez and Wintz, 1987] Gonzalez, R. C. and Wintz, P. (1987). Digital Imagem Processing. Addison-
Wesley Publishing Company, second edition edition.
[Hearn and Baker, 1994] Hearn, D. and Baker, P. (1994). Computer Graphics. Prentice-Hall.
[Mascarenhas and Velasco, 1989] Mascarenhas, N. D. A. and Velasco, F. R. D. (1989). Processamento
digital de imagens. In IV Escola Brasileiro-Argentina de Inform´tica, Universidade Cat´lica de Santiago
a o
del Estero, Termas do Rio Hondo - Argentina.
[Minghim and Oliveira, 1997] Minghim, R. and Oliveira, M. C. F. (1997). Uma introdu¸˜o ` visualiza¸˜o
ca a ca
computacional xvi jai’97. In XVII Congresso da SBC, volume 1777 of Jornadas de Atualiza¸˜o em
ca
Inform´tica, pages 85–131, Bras´ - Brazil.
a ılia
[Persiano and Oliveira, 1989] Persiano, R. C. M. and Oliveira, A. A. F. (1989). Introdu¸˜o ` Computa¸˜o
ca a ca
Gr´fica. Livros T´cnicos e Cient´
a e ıficos Editora Ltda.
[Plastock and Kalley, 1999] Plastock, R. and Kalley, G. (1999). Computa¸˜o Gr´fica. Mc Graw Hill.
ca a
[Schr¨eder, 1998] Schr¨eder, W. (1998). The Visualization Toolkit.
o o
[Schr¨eder et al., 1996] Schr¨eder, W. J., Martin, K., and Lorensen, W. (1996). The Visualization Toolkit
o o
- An Object-Oriented Approach to 3D Graphics. Prentice-Hall.
113

115. Apˆndice A
e
Hist´rico
o
01.11.2003
Novidades
• Apostila de processamento de imagens adicionada.
• Links externos corrigidos.
Problemas
• Os cap´
ıtulos de Rendering e Modelagem ainda est˜o faltando;
a
• Ainda h´ referˆncias com problemas.
a e
27.08.2003
Novidades
• Vers˜o totalmente revisada.
a
Problemas
• Os cap´
ıtulos de Rendering, Modelagem e Processamento de Imagens est˜o faltando;
a
• Algumas referˆncias precisam ser corrigidas.
e
114