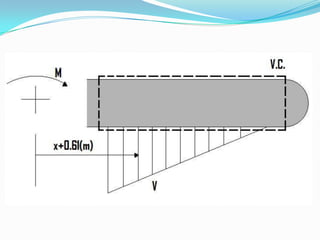
O documento apresenta o cálculo do momento resultante do escoamento de água através de um rasgo em um tubo. Fornece a equação para a variação da velocidade ao longo do rasgo e aplica a equação integral de conservação de quantidade de movimento angular para calcular o momento em torno do eixo do tubo, que é igual a 196.2 N.m.

1. Apresentação do exercício proposto
Elaborado por: Luís Gomes
Marisa Patrão

2. Enunciado
A água escoa horizontalmente para fora de um tubo através de um rasgo de
3
3.175mm, como mostra a figura a seguir representada. A vazão total é de 0.028 m/s
e a velocidade varia linearmente com o máximo numa extremidade do rasgo e
zero na outra. O valor da massa volúmica do fluído é de 998.8452kg/m3 .
Determinar o momento em relação ao eixo do tubo vertical resultante do
escoamento pelo rasgo.
 x 
u  u máx 1  
 1.8288 

3. Para a resolução deste problema, tivemos que recorrer à equação integral de
conservação de quantidade de movimento angular.

A sua dedução começa a partir da segunda lei de Newton. O vector posição ( r )
de uma massa elementar (dm) em relação a um referencial de inércia:
 D 
dF  dmV 
Dt

A equação anterior multiplicada por r , permite obter o balanço do momento,
em relação à origem do sistema de eixos:
  D 
r  dF  r  dmV 

Dt

4. Em que,
    D   D 
D 
r  dmV   V  dmV  r  dmV   r  dmV 
Dt Dt Dt
Esta simplificação acontece porque representa o produto vectorial de
dois vectores paralelos. Então,
 D  

r  dF  r  dmV 
Dt
Considerando a equação, para um sistema finito:
   

 r  dF  
D 
r  dmV    r  V dm
D
Sist. Sist. Dt Dt Sist.

5. Ou designando por M sist a soma dos momentos resultantes da distribuição das
forças de superfície M s e das forças de campo M c :

   DH
M sist MsMc
Dt
Com
  
H   dv   r  V dv
sist sist

Em que o H corresponde a uma propriedade extensiva, neste caso é a quantidade
 

de movimento angular com   r  V . 

DH   
 dv   V  n dA
DT t vc sc

6. Com a equação anterior, teremos a equação integral de conservação de
quantidade de movimento angular:
      
 
    
M s  M c   r  V dv   r  V  V  n dA
t vc sc
Cálculo da velocidade máxima, através da sua variação com o comprimento do
rasgo(equação dada no problema) :
 x 
u  u máx 1  
 1.8288 
L
 x
l *  u máx1  dx  Q
0  L

8. 1.8288
 x 
0.003175  u máx 1.8288 dx  0.0282

1

0
 u máx  9.7547m / s
Agora podemos voltar à equação integral de conservação da quantidade de
movimento angular:
1.8288   x    x 
M  0.003175 * 998.8452   x  0.6096u máx 1   * umáx 1   dx
0   1.8288    1.8288 

9. 1.8288
M  3.171   ( x  0.6096)[9.7547 * (1 
x
)]2 dx
0 1.8288
1.8288
M  3.171   9.7547 x * (1  ) dx
x x 2
)]2  58 * (1 
0 1.8288 1.8288
1.8288
M  3.171   95.154 x  104.06x 2  28.45 x 3  58  63.43x  17.34 x 2 dx
0
1.8288
M  3.171   28.45 x 3  86.72 x 2  31.724 x  58 dx
0

10. 
M  3.171 7.1125 x 4  28.907 x3  15.862 x 2  58 x1.8288
0
M  3.17179.56  176.81  53.05  106.07
M  196.2 N .m