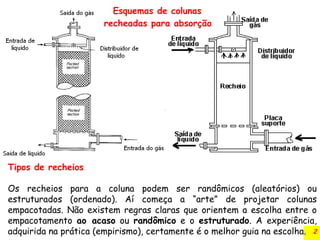
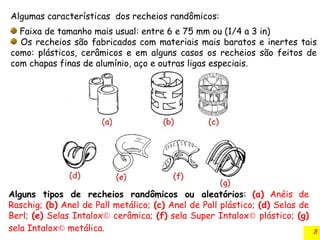
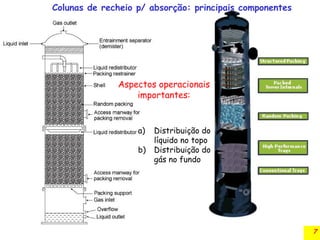
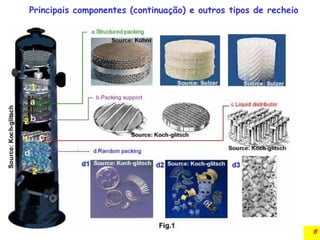
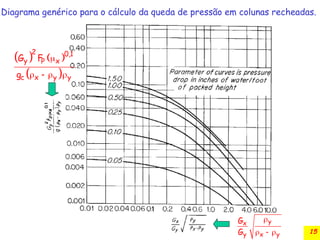
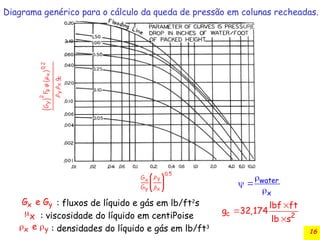
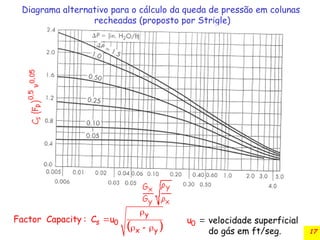
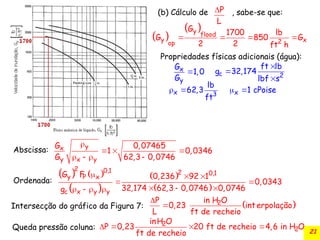
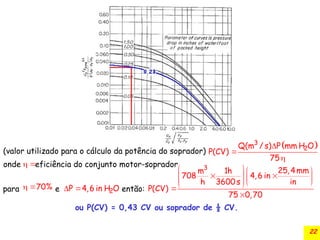
O documento discute a absorção gasosa em colunas de recheio, destacando sua aplicação na remoção de contaminantes de fluxos gasosos e líquidos. Apresenta diferentes tipos de recheios, suas características e especificações, além de considerar aspectos operacionais como a distribuição de líquidos e gases. Também inclui métodos para cálculo do diâmetro da coluna e a queda de pressão durante a operação.

1. 1
ABSORÇÃO GASOSA: Colunas de recheio
Introdução
As colunas de recheio ou empacotadas são usadas com freqüência para
remover os contaminantes presentes num fluxo gasoso (por absorção,
operação em que a transferência de massa ocorre da fase gasosa para a
fase líquida). As colunas de recheio também são aplicadas na remoção de
componentes voláteis de um fluxo líquido, por contato com um gás inerte
com escoamento contracorrente (por dessorção ou esgotamento, ou seja,
a operação inversa da anterior, onde a transferência de matéria é da fase
líquida para a gasosa). Além disso, as torres recheadas, também são
utilizadas na destilação e resfriamento de um líquido. Neste capítulo
estudaremos a operação de transferência de massa denominada de
ABSORÇÃO GASOSA.
Projeto de uma coluna de recheio
Um equipamento muito utilizado par a absorção gasosa é a coluna de
recheio, como mostra esquematicamente a figura a seguir. Para a limpeza
de um gás “sujo” pode-se empregar também uma coluna de estágios (visto
no Capítulo 1).

2. 2
Tipos de recheios
Os recheios para a coluna podem ser randômicos (aleatórios) ou
estruturados (ordenado). Aí começa a “arte” de projetar colunas
empacotadas. Não existem regras claras que orientem a escolha entre o
empacotamento ao acaso ou randômico e o estruturado. A experiência,
adquirida na prática (empirismo), certamente é o melhor guia na escolha.
Esquemas de colunas
recheadas para absorção

3. 3
Algumas características dos recheios randômicos:
Faixa de tamanho mais usual: entre 6 e 75 mm ou (1/4 a 3 in)
Os recheios são fabricados com materiais mais baratos e inertes tais
como: plásticos, cerâmicos e em alguns casos os recheios são feitos de
com chapas finas de alumínio, aço e outras ligas especiais.
Alguns tipos de recheios randômicos ou aleatórios: (a) Anéis de
Raschig; (b) Anel de Pall metálico; (c) Anel de Pall plástico; (d) Selas de
Berl; (e) Selas Intalox cerâmica; (f) sela Super Intalox plástico; (g)
sela Intalox metálica.

4. 4
Alguns tipos de recheios randômicos ou aleatórios (continuação)

5. 5
Alguns tipos de recheio randômico de alto desempenho (High performance
Random Packing) podem se fabricados em aço carbono, aço inoxidável,
cobre, alumínio, titânio, zircônio e outras ligas sob consulta. Oferecem
elevadas áreas específicas (m2
/m3
) para a transferência de massa e baixa
perda de carga.
IMTP e Hy-Pak fabricado pela NORTON (Colunas com recheio de alto
desempenho são mais eficientes que as colunas de estágios)
IMTP Hy-Pak

6. 6
Recheios estruturados

7. 7
Colunas de recheio p/ absorção: principais componentes
Aspectos operacionais
importantes:
a) Distribuição do
líquido no topo
b) Distribuição do
gás no fundo

8. 8
Principais componentes (continuação) e outros tipos de recheio

9. 9
T i p o M a t e r i a l
T a m a n h o
n o m i n a l ,
i n
D e n s i d a d e
B u l k ,
l b / f t 3
Á r e a
e s p e c í f i c a ,
f t 2
/ f t 3
P o r o s i d a d e
F a t o r d e
e p a c o t a m e n t o
P P
F f
A n é i s
R a s c h i g
C e r â m i c o
½
1
1 ½
2
5 5
4 2
4 3
4 1
1 1 2
5 8
3 7
2 8
0 , 6 4
0 , 7 4
0 , 7 3
0 , 7 4
5 8 0
1 5 5
9 5
6 5
1 , 5 2
1 , 3 6
1 , 0
0 , 9 2
A n é i s
P a l l
M e t a l
P l á s t i c o
1
1 ½
2
1
1 ½
3 0
2 4
2 2
5 , 5
4 , 8
6 3
3 9
3 1
6 3
3 9
0 , 9 4
0 , 9 5
0 , 9 6
0 , 9 0
0 , 9 1
5 6
4 0
2 7
5 5
4 0
1 , 5 4
1 , 3 6
1 , 0 9
1 , 3 6
1 , 1 8
S e l a s
B e r l C e r â m i c a
½
1
1 ½
5 4
4 5
4 0
1 4 2
7 6
4 6
0 , 6 2
0 , 6 8
0 , 7 1
2 4 0
1 1 0
6 5
1 , 5 8
1 , 3 6
1 , 0 7
S e l a s
I n t a l o x 
C e r â m i c a
½
1
1 ½
2
3
4 6
4 2
3 9
3 8
3 6
1 9 0
7 8
5 9
3 6
2 8
0 , 7 1
0 , 7 3
0 , 7 6
0 , 7 6
0 , 7 9
2 0 0
9 2
5 2
4 0
2 2
2 , 2 7
1 , 5 4
1 , 1 8
1 , 0
0 , 6 4
S u p e r
I n t a l o x 
C e r â m i c a 1
2






6 0
3 0
1 , 5 4
1 , 0
I M T P  M e t a l
1
1 ½
2






0 , 9 7
0 , 9 8
0 , 9 8
4 1
2 4
1 8
1 , 7 4
1 , 3 7
1 , 1 9
H y - P a k M e t a l
1
1 ½
2
1 9

1 4
5 4

2 9
0 , 9 6

0 , 9 7
4 5
2 9
2 6
1 , 5 4
1 , 3 6
1 , 0 9
Características de
alguns tipos de
recheios randômicos
FP : fator para a perda
de carga e fP
coeficiente relacionado
à transferência de
massa (sistema NH3
-
água)

10. 10
P
F

11. 11
Contato entre o gás e o líquido na coluna de recheio:
Definições preliminares:
= fluxo mássico de líquido na coluna (lb/ft2
h)
= fluxo mássico de gás na coluna (lb/ft2
h)
A figura a seguir mostra dados experimentais típicos de queda de
pressão em função do fluxo de ar numa coluna de recheio.
x
G
y
G
Queda de pressão na
coluna de recheio (selas
Intalox de 1 in) para o
sistema ar-água.
 

y x
P
log versus log G para valores de G para um tipo de recheio
L

12. 12
Considerações sobre a figura anterior
a) Recheio seco (Dry) ou:
linha reta:
Eq. de ERGUN (OP1):
Para: velocidade superficial do gás e densidade média do gás
b) Recheio irrigado:
i) A queda de pressão aumenta em relação ao recheio seco, para um
mesmo valor de , porque o líquido no interior da torre ocupa um
determinado espaço destinado ao fluxo de gás;
ii) Para um certo fluxo de líquido e valores moderados de não se
observa retenção de líquido na coluna, e a relação é
LINEAR e paralela a linha de recheio seco;
iii) Para um certo fluxo de líquido e valores maiores de começa a se
observar a certa retenção de líquido na coluna, nesse caso a relação
deixa de ser LINEAR. Exatamente no ponto do
diagrama onde a relação deixa de ser linear é denominado de PONTO
DE CARGA (loading point) ponto C (condição operacional desejável);
iv) Para incrementos de fluxo de gás (após o loading point) a queda
de pressão aumenta rapidamente e as linhas de
são praticamente verticais (queda de pressão do gás; maior ou igual a 2
in de H2
0/ft de recheio);
y
G
x
G y
G
 

y
P
log vs. log G
L
y
G
 

y
P
log vs. log G
L
y
G
 

y
P
log vs. log G
L
 
 
   
  
  

 
 
 
2
2
y 0
0
2 3
2 2 p
p
1,75 1 u
150 1 u
P
L d
d

0
u y
 

13. 13
v) Aumentando um pouco mais ,a quantidade de líquido acumulada no
interior da coluna e tal que impede a passagem de gás e essa condição
limite INDESEJÁVEL é denominada de velocidade de INUNDAÇÃO
(flooding point), ponto I da figura;
y
G
Considerações gerais sobre o contato gás-líquido em colunas de recheio:
Não é FÁCIL a identificação do diagrama os pontos de
carga (C) e de inundação (I). Mais o engenheiro tem que saber prever, a
partir de diagramas ou correlações empíricas, as condições de
INUNDAÇÃO da coluna.
A figura a seguir mostra um digrama experimental para a determinação do
fluxo de inundação da coluna.
Um diagrama largamente utilizado para determinar a queda e pressão em
coluna recheada para absorção é mostrada na próxima figura. Nessa
figura os adimensionais característicos da absorção gasosa são:
Abscissa:
Ordenada:
 

y
P
log vs. log G
L

  
y
x
y x y
G
G
   
 

   
2 0,1
y x
P
c x y y
G F
g
As variáveis dos adimensionais devem
(necessariamente) serem expressas em:
: fluxos de líquido e gás em lb/ft2
s
: viscosidade do líquido em centiPoise
: densidades do líquido e gás em lb/ft3
x y
G e G
x
 
x y
e

c 2
lbf ft
g 32,174
lbs

14. 14
Para quedas de pressão ( ) maiores 1,5 in e H2
0/ft de recheio a coluna
DEVE estar da iminência ou muito próxima da condição de inundação.
Pode-se utilizar também uma correlação empírica para calcular a queda de
pressão na condição de inundação:
P/L
 
 


 

 

0,7
floo
2
d. P
P
in H O
ft recheio
P 0,115 F
p / 10 F 60
Fluxo de gás de inundação para selas Intalox cerâmicas ( sistema ar-água).



P
2
Para F 60 :
in H O
P
2,0
L ft recheio
coluna inundada

15. 15
Diagrama genérico para o cálculo da queda de pressão em colunas recheadas.

  
y
x
y x y
G
G
   
 

   
2 0,1
y x
P
c x y y
G F
g

16. 16

 

water
x
x y
G e G
x
 
x y
e
: fluxos de líquido e gás em lb/ft2
s
: viscosidade do líquido em centiPoise
: densidades do líquido e gás em lb/ft3



c 2
lbf ft
g 32,174
lb s
Diagrama genérico para o cálculo da queda de pressão em colunas recheadas.

17. 17
Diagrama alternativo para o cálculo da queda de pressão em colunas
recheadas (proposto por Strigle)
 


  
y
s 0
x y
Factor Capacity : C u 
0
u velocidade superficial
do gás em ft/seg.

18. 18
Velocidade de inundação para coluna com recheio estruturado

0,f
u velocidade de inundação em m/s Mellapak SULZER
Montz B1 MONTZ
Gempak KOCK-GLITSCH

19. 19
Cálculo do diâmetro da coluna de recheio para Absorção (DT
)
O diagrama da Figura 7 também pode ser utilizado para calcular o diâmetro da
coluna ( ) de recheio da seguinte forma:
T
D
 


2
T
T
D
A
4

'
x
x
T
G
G
A
e 
'
y
y
T
G
G
A
 

     
'
y y
x x
'
y x y x y
y
assim,
G G
G G

  
'
y
x
'
x y
y
G
G
P
L
   
 

   
2 0,1
y P x
c x y y
G F
g
 
  
P x x y
F , , e y
G
 

 
' 2
y T
T
y
G D
A
G 4


'
y
T
y
4G
D
G
então: (diâmetro da coluna de recheio)
Área da secção transversal da coluna:
com e a queda de pressão obtém-se a ordenada
com as condições operacionais pode-se calcular e depois:
Exemplo 1: Cálculo do diâmetro e queda de pressão para a coluna de absorção.
Uma torre de absorção com recheio constituído de selas Intalox de 1 polegada
(25,4 mm) é empregada para “limpar” 25000 ft3
(708 m3
) de gás por hora. O gás à
entrada da coluna, à temperatura e 68°F (20ºC) e a 1,0 atm, contém 2,0% (volume)
de amônia. Água pura é utilizada como solvente absorvedor. A razão entre as taxas
de gás e água é de 1,0 lb de gás para 1,0 lb de líquido. Calcular:
(a) O diâmetro da coluna, para um fluxo de gás igual à metade da condição de
inundação,
(b) Qual a queda de pressão na coluna se o recheio tem 20 ft (6,1m) de altura.

20. 20
Solução:
Cálculo do peso molecular médio do gás à entrada da coluna (98% de ar e 2% de
NH3
):     
y
lb
PM 29 0,98 17 0,02 28,76
lbmol



3
ft atm
R 0,7302
lbmol R
       
R T( F) 460 68 460 528 R
 


   
 


y
y 3 3
lb
28,76 1,0 atm
PM P lb mol lb
0,0746
R T ft atm ft
0,7302 528 R
lb mol R
 
'
x x
'
y y
G G
1
G G
   

y 2
flood
lb
G 1700 inundação
ft h
ou   
y 2
flood
lb
G 0,472
ft s
 
 
  
y
flood
y 2
op
G 0, 472 lb
G 0,236
2 2 ft s
   
3
'
y 3
ft 1 h lb lb
G 25000 0,0746 0,518
h 3600 s s
ft
 

   
' 2
y T 2
y
2
lb
0,518
G D
s
Área 2,19 ft
lb
G 4
0,236
ft s
Constante dos gases ideais:
então, a densidade media do gás é :
(a) Utilizando a Figura 6 (selas Intalox de 1 in), para temos:
A taxa mássica total de gás é:
A coluna deve operar com:

T
D 1,67 ft (509 mm)

21. 21
(b) Cálculo de , sabe-se que:
 
 
   
y
flood
y x
2
op
G 1700 lb
G 850 G
2 2 ft h
 
x 3
lb
62,3
ft
 
x 1 cPoise



c 2
ft lb
g 32,174
lbf s

x
y
G
1,0
G
Propriedades físicas adicionais (água):
P
L
Abscissa:
Ordenada:

  
   
y
x
y x y
G 0,07465
1 0,0346
G 62,3 0,0746
   
 


   
2 0,1
y P x
c x y y
G F
g
 
 
 

  
2 0,1
0,236 92 1
0,0343
32,174 62,3 0,0746 0,0746
Intersecção do gráfico da Figura 7:  

 2
P in H O
0,23 interpolação
L ft de recheio
   
2
2
inH O
P 0,23 20 ft de recheio 4,6 in H O
ft de recheio
Queda pressão coluna:

22. 22
(valor utilizado para o cálculo da potência do soprador)
 



3
2
Q(m /s) P mm H O
P(CV)
75
 
  2
P 4,6 in H O
 70%
   
 
   
   
 


3
25,4mm
m 1h
708 4,6 in
h 3600s in
P(CV)
75 0,70
onde eficiência do conjunto motor-soprador
para e então:
ou P(CV) = 0,43 CV ou soprador de ½ CV.

23. 23
Esquema típico com colunas de absorção-dessorção

24. 24
Balanço material global no volume de controle:
(1)
Balanço material global para o componente A (soluto) no
volume de controle:
(2)
a a
L V L V
  
a a a a
L x V y L x V y
  
Explicitando y na Eq. (2), temos a Linha de Operação para
absorção em coluna de recheio:
a a a a
V y L x
L
V V
y x

 
Princípios da Absorção
(3)
Na Eq. (3) x e y representar a composição bulk das fases
em contato. Naturalmente, em problemas reais tem-se que
rigorosamente: V, L, x e y depende da posição no interior da
coluna.
Condição limite para razão gás-líquido na coluna de recheio:
Para a determinada taxa de gás à entrada ( ), qual a menor
taxa molar de líquido à entrada da coluna ( ).
min.
L
b
V
a
L
Definições preliminares:
V e L: taxas molares de gás e líquido num determinado ponto (mesma posição) no
interior da coluna, respectivamente.
y e x: frações molares de soluto (A) no gás e líquido no mesmo ponto citado
anteriormente.

25. 25
A figura mostra a representação da LO para absorção gasosa ou a Equação 3
Para sistema diluídos: , ou Linha
de Operação LINEAR
(4)
(5)
L
constan te
V

a
b
a
b
op.
y y
L
V x x

 

 

 
a a
b b
min.
* *
min. a a
b b
y y y y
L
ou L V
V x x x x
 
 
 
   
   
   
 
Na condição de taxa MÍNIMA de líquido na coluna
de absorção, o líquido absorvedor encontra-se
saturado (equilíbrio com o gás) na base da coluna.
Taxa de Absorção
Princípios da transferência de massa entre as fases na interface gás-líquido (teoria
do duplo filme) para a destilação e absorção gasosa é representada nas figuras a
seguir:
A = componente mais volátil A = soluto muito solúvel

26. 26
Soluto muito solúvel ????
Inclinação “local” da relação de equilíbrio m ou H assume um valor muito PEQUENO
o que vale dizer mesmo para um gás diluído que:
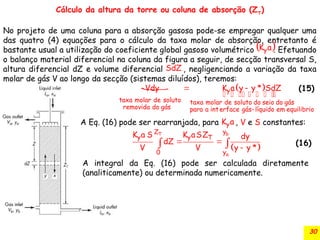
A taxa molar de ABSORÇÃO na coluna por unidade de volume, da teoria de duplo
filme, é dada pelas seguintes relações:
(6)
(7)
(8)
xA
e xAi
= fração molar do soluto no líquido bulk e na interface, respectivamente
yA
e yAi
= fração molar do soluto no gás bulk e na interface, respectivamente
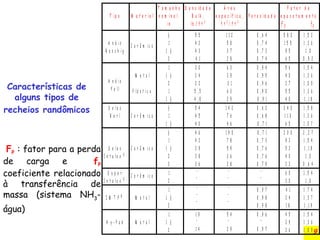
a = área interfacial específica (por unidade de volume), que é uma característica do
tipo de recheio [ft2
/ft3
de recheio];
 
y A Ai
r k a y y
 
 
x Ai A
r k a x x
 
*
A
x e
   
* *
y A A x A A
r K a y y K a x x
   
*
A
y fração molar do soluto em equilíbrio nas fases
e : coeficientes individuais ou peliculares molares de transferência de massa,
nas fases gasosa e líquida, respectivamente ou ;
e : coeficientes globais molares de transferência de massa, nas fases gasosa
e líquida, respectivamente ou .
y
k x
k
 
 
 
 
2
kg mol
s m
2
lbmol
h ft
 
 
 
 
y
K x
K
2
lbmol
h ft
 
 
 
 
 
 
 
 
2
kg mol
s m

27. 27
Unidades de r (taxa molar de
absorção por unidade de volume)
 
2
2 3 3
fração molar
lbmol lbmol
ft
r adimensional
h ft ft h ft
 
 
  
 
 
 
      
A composição do soluto na interface pode ser obtida, a partir da Linha do
Operação, e das Eqs. (6) e (7):
 
i i
x, y
i x
i y
y y k a
x x k a



Obs: para calcular as composições na interface precisamos do conhecimento dos
coeficientes peliculares na fase líquida e gasosa, como mostra a figura a seguir.
(9)
x e y coordenadas da Linha de Operação

  i i x
i i y
y y y y k a
tan g
x x x x k a
 
   
 
inclinação “local” da linha de equilíbrio (y*=mx+b) para o ponto com
coordenadas (x, y) e (xi
, yi
):
*
i
i
y y
m
x x



Resistência à TM (predominantemente) na fase líquida ou
solubilidade do soluto no solvente é baixa:
x y
k a k a
  

 
   
 

i
i
i
y y
0 tan g 0 ou y y
x x
 
i
x x x *

28. 28
Para facilitar o entendimento (alguns exemplos):

x y
k a k a 



i
i
y y
1
x x
  
45
Caso 1:
O caso 2 (situação desejável): máxima força motriz na fase gasosa
   

 5
x y soluto muito so
k a 10 k a lúvel

 

5
i
i
y y
10
x x
   
i
0 e y y *
Gás saturado na interface ou negligenciável
a resistência à TM na fase líquida
 

i
y y *
 
 i
x x
Caso 2:
 

y y *

29. 29
O força motriz na Absorção Gasosa é: (linhas verticais no diagrama y vs. x).
Os Coeficientes Globais molares de transferência de massa são determinados
conhecendo-se os coeficientes locais ou individuais e a inclinação local da curva de
equilíbrio (m) (Incursão em FT):
Reescrevendo a Eq. (8), teremos:
(10)
Substituindo as Eqs. (6) e (7) na Eq. (10), teremos:
(11)
Observar que a inclinação local da Linha e Equilíbrio é dada por (ver figura anterior)
(12)
Dessa forma teremos:
(13)
Similarmente:
(14)
y y *

     
i i
y
y y * y y *
1
K a r r
y y
r
  
  
 
 
 
 
y i
y x
i
i
i
k a y y
y y *
k a x
y
K a
y
1
x


 


i
i
y y *
m
x x



y y x
1 1 m
K a k a k a
 
x x y
1 1 1
K a k a mk a
 
Obs: Sistemas de absorção de elevada solubilidade: x elevado ou pequ
k a m eno
y y
1 1
K a k a


30. 30
Cálculo da altura da torre ou coluna de absorção (ZT
)
No projeto de uma coluna para a absorção gasosa pode-se empregar qualquer uma
das quatro (4) equações para o cálculo da taxa molar de absorção, entretanto é
bastante usual a utilização do coeficiente global gasoso volumétrico . Efetuando
o balanço material diferencial na coluna da figura a seguir, de secção transversal S,
altura diferencial dZ e volume diferencial , negligenciando a variação da taxa
molar de gás V ao longo da secção (sistemas diluídos), teremos:
 
y
K a
SdZ
  
y
taxa molar de soluto taxa molar de soluto do seio do gás
removida do gás para a interface gás líquido em equilibrio
Vdy K a y y * SdZ

  
      
 
b
T
a
y
Z
y y T
0 y
K a S K aSZ dy
dZ
V V y y *
 

 
A Eq. (16) pode ser rearranjada, para , V e S constantes:
y
K a
(15)
(16)
A integral da Eq. (16) pode ser calculada diretamente
(analiticamente) ou determinada numericamente.

31. 31
Unidades de Transferência
A Eq. (16) pode ser reescrita:
Número de unidades de transferência (NTU): , a integral da Eq. (17);
que fisicamente representa a mudança da composição do gás na coluna (dy) dividido
pela força motriz média na coluna ou seja: . O subscrito
Oy denota que a força motriz é global (O) e na fase gasosa (y).
Altura da unidade de transferência (HTU): , a outra parte da Eq. (17)
que tem a dimensão de comprimento.
(18)
Como determinar ???
 
b
T
y a
dy
V /S
Z
K a y y *



 
b
Oy
a
dy
N
y y *



   
Oy a
b média
N y y / y y *
  
Oy
y
V /S
H
K a

Oy OY
T
Z N H
 
Oy Oy
N e H
(17)
 Diagrama y* vs. x, Linha Operação e Recuperação desejada.
 Condições operacionais + correlações para transferência de massa ou
diagramas/figuras, usualmente disponíveis para recheio e sistemas mais comuns
Oy
N
Oy
H
Relação entre o Número de Unidades de Transferência (NTU) e Número Teórico
de Pratos (NTPN)
HTU NTU

32. 32
NTU = NTP, quando as Linhas de Operação e Equilíbrio forem lineares e
paralelas, nesse caso:
[Figura 13 (a)] (19)
NTU > NTP, quando as Linhas de Operação e Equilíbrio forem lineares e
divergentes [Figura 13(b)] ou seja, a inclinação da LO for maior que da LE.
Figura 13 Relação entre NTU e NTP.
a
b
OY
y y
N N
y y *

 

     
 
 
 
 
 
 
 

 
 

 
   
    
 
    
 
 
 
 
 
   
 

 
*
b b
*
a a
b a b a
Oy * *
ML b b a a b a
* * *
b b b a
*
a a
y y
ln
y y
y y y y
NTU N NTP
y y y y y y y
ln
y y y y
ln
y y
(20)
Kremser

33. 33
Obs: Substituir alguns valores para fazer a verificação:
Exemplo:
Relação de equilíbrio:
*
a a
x 0 y 0
   a
b
recuperação : y 0,03 y 0,001
  
*
b
y 0,9x e x 0,01 o que vale d er
, iz
  *
b
y 0,009

   
 
 
 
 
 
 
Oy
0,03 0,001
NTU N 4,41
0,03 0,009 0,001 0
0,03 0,009
ln
0,001 0
0,03 0,009
ln
0,001 0
NTP 2,60
0,03 0,001
ln
0,009 0

  
  
 

 

 
 

 

 
 
 

 

 
NTU > NTP

 
a
b
Oy
ML
y y
N
y



 
   
 
 
* *
a a
b b
ML *
b b
*
a a
y y y y
y
y y
ln
y y
  
 
 

 
 

 
 
Quando as Linhas de Operação e Equilíbrio forem LINEARES, o Número de Unidades
de Transferência é o quociente entre a variação de composição do gás e a diferença
média logarítmica na fase gasosa:
Assim,
(21)
(22)

34. 34
A equação correspondente a Eq. (21), para a fase líquida é:
Quando o líquido absorvedor estiver isento de soluto, i.e. e , expressão
alternativa que utiliza o fator de absorção pode ser utilizada:
 
a
b
Ox
ML
x x
N
x



a
x 0
 *
a
y 0

L
A
mV

 
a
b
Oy
y y (A 1) 1
A
N ln
A 1 A
 
 
  
  
mV
S
L

 
a b
Ox
x x (S 1) 1
S
N ln
S 1 S
 
 
  
  
A equação correspondente a Eq. (24) para o caso de STRIPPING (limpeza do
líquido) para o gás livre de soluto que utiliza o fator de stripping , teremos:
(23)
(24)
(25)
 
y y y y
T
y i
V S dy
Z H N para H e N
k a y y
  


 
x x x x
T
x i
L S dx
Z H N para H e N
k a x x
  


 
  


T Oy Oy Oy Oy
y
V S dy
Z H N para H e N
K a y y *
 
Ox Ox Ox Ox
T
x
L S dx
Z H N para H e N
K a x * x
  


“Filme” líquido
“Filme” gasoso
Gás global
Líquido global
A altura da coluna de recheio para pode ser calculada empregando 4 equações:
(26)
(27)
(28)
(29)

35. 35
Similarmente para o filme líquido pode-se expressar os coeficientes de TM,
empregando a diferença de concentração volumétrica do soluto no lugar da fração
molar de soluto no líquido. Reescrevendo os coeficientes na fase líquida, teremos:
y
g
k a
e
k a
P

y
g
K a
K a
P

g g
k a e K a 3
lbmol
hft atm
 
 

 
 
x
L
Mx
k a
k e
a 

x
L
Mx
K a
K a 

Formas alternativas para os coeficientes de transferência de massa:
Os coeficientes de transferência de massa no filme gasoso reportado na literatura
podem ser expressos utilizando como força motriz a diferença de pressão parcial
do soluto no lugar da fração molar de soluto no gás. Reescrevendo os coeficientes no
gás, teremos:
onde P = pressão operação coluna. Unidades usuais para
onde = densidade molar do líquido (kmol/m3
ou lbmol/ft3
). Unidades usuais:
Mx
(30)
(31)
L L
k a e K a 1
3
3
-
lb mol
ft
lbmol
ou h
hft
 
 
 
 
 
 

 
 
 
 
Substituindo V/S (fluxo molar de gás) por , nas Eqs. (26) e (28) e L/S
(fluxo molar de líquido) por , nas Eqs. (27) e (29), Podemos reescrever as
alturas de unidade de transferência, considerando

y
M
G
G
M
 x
M
G
L
M
M x
M 
 
 
A g A Ai
A y A A
A
i
A
r N k a p p
r N k a y
e p y
y
P
   






 
 
 
A L Ai A
A x Ai A
A A Mx
r N k a c c
r N k a x
c
x
e x


  


  




36. 36
'
y
G taxa mássica de gás
 
y
G fluxo mássico de gás
M
y
y g
G
V S
H
k a k aP
e
  M
Oy
y g
G
V S
H
K a K aP
 

   
 
M x x x
x
x L M L M L
L G M G
L S
H
k a k a k a k a
e x x
Ox
x L
G
L/S
H
K a K a

 
2 2
kg/m h ou lb/ ft h
 
 
M
G fluxo molar de gás na coluna
  
 
 
2 2
kgmol/ m h ou lb mol/ ft h
3 3
kg/m ou lb/ft
 
 
Cuidado com a nomenclatura:

V taxa molar de gás
y
G fluxo mássico de gás

M
L fluxo molar de líquido na coluna
  
 
 
2 2
kgmol/ m h ou lb mol/ ft h
x
G fluxo mássico de líquido

x densidade do líquido
 
y y x
1 1 m
K a k a k a
ou
 
 
  
    
M
Oy y
x
M
M
y y x
G
H H
m H
M M M
L
M
m
K a k a
L
ou
k
a
G G G
L
a
inda M
Oy y x
M
G
H H m H
L
 
Reescrevendo a Eq. (14), considerando as Eqs. (32) e (33), teremos:
(32)
(33)
(34)

M
G fluxo molar de gás
Importante: em muito problemas de OP2, conhecemos Hy e Hx ou essas alturas
podem estimadas por correlações. Assim a altura da coluna de recheio ZT pode ser
calculada por: e precisamos das variáveis: m, GM, LM, e NOy

T Oy Oy
Z H N

37. 37
Exemplo (Provão 1998): Uma coluna de absorção (ver figura) com área de secção
transversal de 0,29 m2
, contendo anéis de Raschig de ½ in é utilizada na
recuperação de amônia de uma corrente de ar. A coluna, que opera a 25 °C e 1, 0
atm, recebe uma mistura ar-amônia (massa molar de 29 g/mol) com fração molar de
0,005 de amônia a uma vazão de 20 mol/h. O gás estabelece contato com uma
corrente de água cuja vazão é de 20 mol/h. Nas condições praticadas, considerando
o recheio e o sistema ar-amônia sob pressão atmosférica, a altura de uma unidade
de transferência (HTU) é dada por:
A relação de equilíbrio é dada por: p = 1,12 x , sendo p a pressão parcial de amônia
no ar e x é fração molar de amônia na fase líquida. Considerar L e G constantes ao
longo da coluna. Supondo o processo controlado pela etapa de transferência de
massa no filme gasoso e desejando um percentual de recuperação de 75%, calcule a
altura da coluna para uma operação com fluxos contracorrentes.
Lembre-se que o número de unidades de transferência (NTU) é calculado pela
expressão:
em que y é fração molar de amônia na fase gasosa e y* é a fração molar de amônia
em equilíbrio com a fase líquida.
0,1 0,39
Oy
H 0,35G L para

 Oy 2
kg
H [metros] e G e L
m h
 
 
 
 
b
a
y
Oy
y
dy
N
y y *




38. 38
Solução:
Altura da coluna:
Cálculos dos fluxos mássicos de gás (G) e de líquido (L) na coluna de recheio:
Oy Oy
T
Z N H
 
3
2 2
kg
mol
20 29 10
kg
h mol
G 2
0,29 m h m


 
3
2 2
kg
mol
20 18 10
kg
h mol
L 1,24
0,29 m h m


 
Obs: Nomenclatura do Provão
Cálculo da Altura de Unidade de Transferência :  
Oy
H
    0,39
0,1
0,1 0,39
Oy
H 0,35G L 0,35 2 1,24 0,345 m


  
Linha de Operação para Absorção:
ou para sistema diluído ( ) e para L=V, teremos:
a a a a
V y L x
L
y x
V V

 
a a
V V e L L
 
a a
a a
V y L x
L
y x x y x
V V
(1)

    
(água pura)
a
x 0

Cálculo de ??
Recuperação de 75% :
a
y
a
b
b
y y
0,75 ou
y

 a b b
y y 0,75y 0,005 0,75 0,005
    
3
a
y 1,25 10
 3
x y 1,25 10
 
Substituindo ya na Eq. (1), teremos: (2)

39. 39
Relação de equilíbrio: e (gás IDEAL), como P = 1,0 atm então:
(3)
Força motriz global:
Cálculo do Número de Unidades de Transferência
Mudança de variável: w = 0,0014 – 0,12y então:
p 1,12x

*
p y P

p y* 1,12x
   
3
y* 1,12 y 1,2510
 
y y*
   
3
y 1,12y 1, 410 0,0014 0,12y

   
 
Oy
N
 
b
a
y
Oy
y
dy
N o
y *
u
y



b
a
y 0,005
Oy
y 0,00125
dy
N
0,0014 0,12y





dw 0,12dy

 
b
a
w
0,005
Oy 0,00125
w
1 dw 1 1
N lnw ln 0,0014 0,12y
0,12 w 0,12 0,12

 
   
 

 
 
Oy
0,0014 0,12 0,005
1
N ln 3,72
0,12 0,0014 0,12 0,00125
 
 

 
 
 

 
 
 
Oy Oy
T
Z N H 3,72 0,345 m 1,28 metros
    
Substituindo (2) em (3) teremos: i

40. 40
Packed versus Plate Columns
 Pequenas colunas recheadas (D < 2,0 m) são mais baratas;
 Vários tipos de recheios: materiais inertes com boa resistência química
e compatíveis com líquidos corrosivos;
 Boa eficiência (recuperações elevadas) com baixa queda de pressão e
adequadas para operar com vácuo;
 Podem operam com fluidos que formam espumas;
 Holdup ou retenção de líquido é menor.
 A etapa de limpeza dos pratos é mais simples;
 Alguns tipos de recheio (mais baratos: plásticos), entretanto têm baixa
resistência mecânica (podem danificar ou quebrar);
 Podem operar com taxas/fluxos de líquidos maiores, como conseqüência
uma operação mais econômica;
 Operação com valores baixos de taxas/fluxos de líquido e menos
problemática que coluna recheada (parte do recheio não “molhado”).
Vantagens: Packed Column (coluna recheada)
Vantagens: Plate Column (coluna de pratos)



41. 41
De uma maneira geral as torres recheadas são recomendadas quando o sistema
é corrosivo, viscoso e com tendência a formação de espuma, e o projeto exige
baixo P, pequenos diâmetros (DT < 4ft) e elevados números de estágios.
Os equipamentos mais usuais para absorção são as torres de pratos e torres
recheadas. A escolha deve ser feita em função de vários critérios. A literatura
mais específica apresenta algumas características que nos auxiliam a escolher a
torre mais conveniente.
As torres de prato por sua vez são recomendadas quando o sistema exige
limpezas constantes, e o projeto exige diâmetros maiores (DT > 4ft),
consideráveis taxas transferência de calor e maior flexibilidade de vazões ou
taxas de líquido e gás.
O projeto destas torres é semelhante ao das torres de pratos
ou outras, envolvendo considerações ligadas à operação
mecânica e eficiência do equipamento.
TORRES RECHEADAS
As considerações mecânicas de interesse nas torres são:
- P
- Capacidade
- Distribuidores e suportes

42. 42
Os fatores relacionados com a eficiência do equipamento são:
- Distribuição e redistribuição de líquido;
- Área de contato gás-líquido.
Alguns princípios que devem ser lembrados no projeto:
· A torre deve ser projetada para operar na região de carga
loading (40 a 80% do flooding). Isto determina uma área
considerada ótima para uma eficiência máxima.
· A dimensão do recheio não deve ser maior do que 1/8 do
diâmetro da torre.
· A altura de cada secção de recheio é limitada a
aproximadamente 3DT para anéis de Raschig e 5DT para anéis de
Pall. Não é recomendado utilizar-se secção recheada maior que
20ft.
· Para sistema em que a resistência localiza-se
predominantemente na fase gasosa, recomenda-se utilizar
recheio com distribuição aleatória na coluna. Caso contrário usar

43. 43
Alguns princípios que devem ser lembrados no projeto:
Para diâmetros de recheio maiores de 2” não é econômico utilizar
recheio distribuído aleatoriamente. A distribuição e
redistribuição do líquido na coluna é importante para corrigir a
migração do líquido para as paredes (porosidade maior).
A seqüência de projeto de uma torre recheada é a seguinte:
- Escolha do recheio
- Determinação do diâmetro
- Determinação da altura
- Avaliação da perda de carga
Altura de recheio equivalente a um prato teórico/equilíbrio
Height Equivalent to a Theorethical (equilibrium) Plate (HETP) ou
Height Equivalent to a Theorethical (equilibrium) Stage HETS)
  T
Z
HETP HETS
N
Altura de recheio equivalente a um prato teórico/equilíbrio
N = Número Ideal ou teórico de Estágios
ZT = Altura da coluna de recheio

44. 44
Questão 46 (Engenheiro Processamento Junior 2011).
Uma torre absorvedora com 2 metros de altura de leito recheado realiza uma
separação correspondente a 5 estágios de equilíbrio. Nessa condição, o HETP
desse leito recheado será:
(A) 0,4 m
(B) 2,0 m
(C) 2,5 m
(D) 5,0 m
(E) 10,0 m
   
T
Z 2
HETP HETS 0,4
N 5
Questão 47 (Engenheiro Processamento Junior 2011). Pratos e recheios são
internos de torres, sendo empregados para promover o íntimo contato entre as fases
líquido e vapor numa torre de destilação. Para que os mesmos operem com uma
eficiência adequada de transferência de massa, é preciso que as condições
hidrodinâmicas da operação destes internos sejam adequadas. Comparando-se os
diferentes tipos de pratos e recheios, sabe-se que
(A) os recheios estruturados apresentam pior desempenho (eficiência de transferência
de massa e capacidade) do que os recheios randômicos. Errado
(B) os pratos valvulados são menos sujeitos aos problemas de gotejamento
(weeping) e arraste (jet flooding) do que os pratos perfurados. Certo
(C) entre os tipos usuais de pratos, aqueles dotados de borbulhadores são os que
apresentam menor flexibilidade operacional. Errado
(D) entre os tipos usuais de pratos os perfurados são os menos sujeitos aos problemas
de gotejamento (weeping) e arraste (jet flooding). Errado
(E) nos recheios randômicos o HETP é uma função diretamente proporcional ao tamanho
nominal do recheio, não importando a sua dimensão. Errado