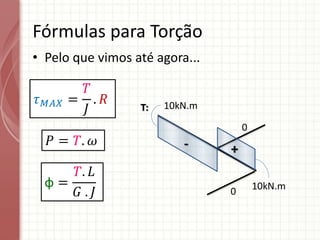
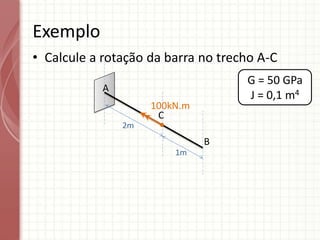
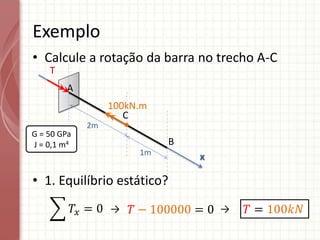
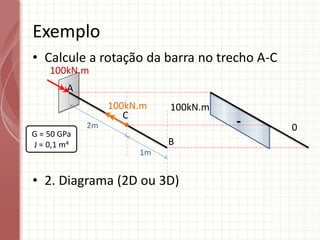
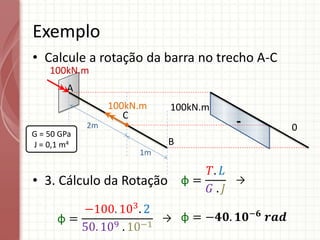
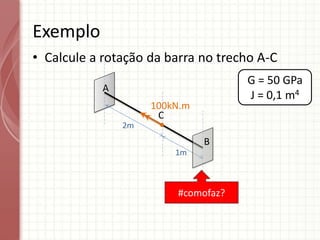
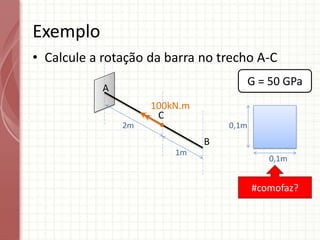
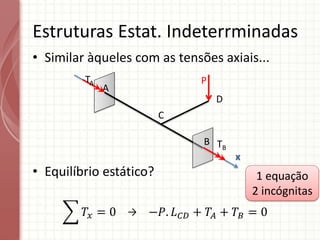
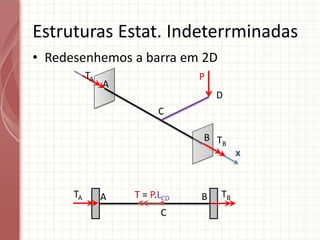
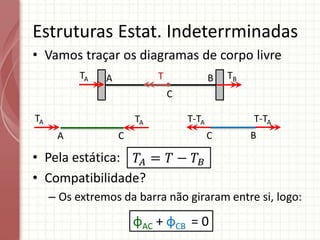
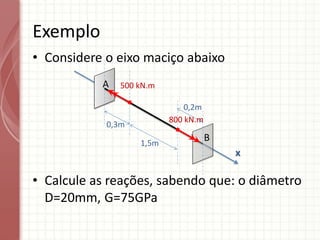
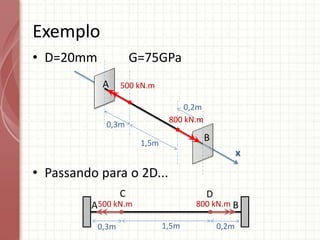
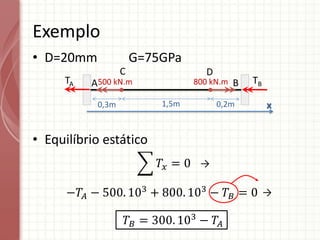
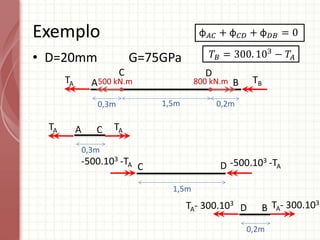
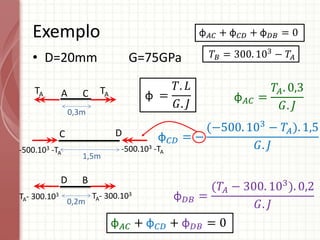
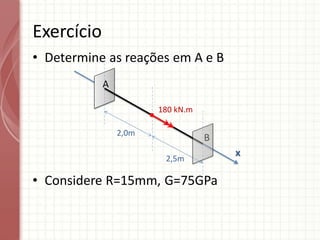
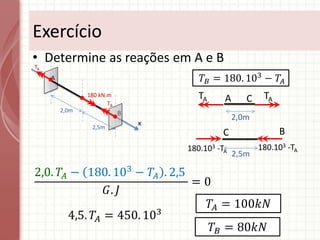
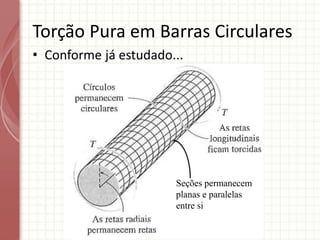
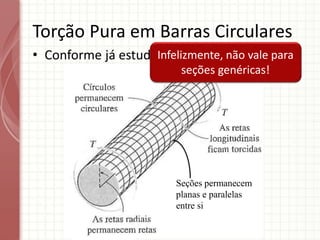
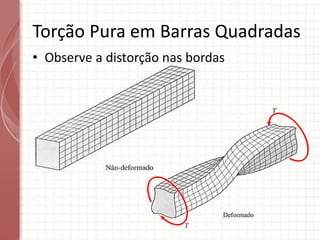
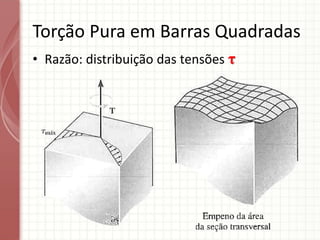
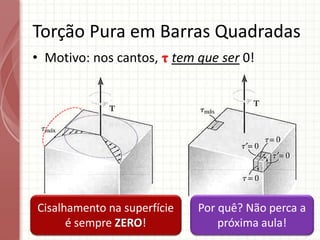
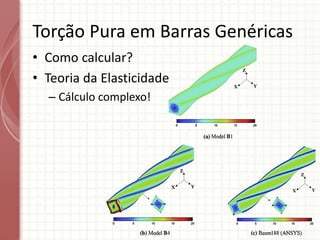
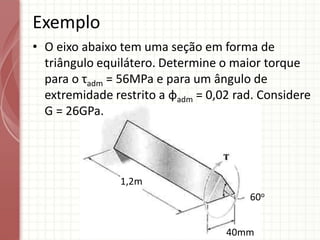
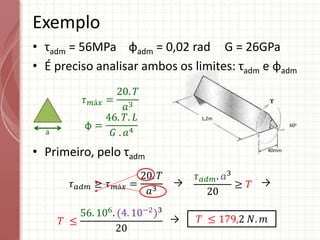
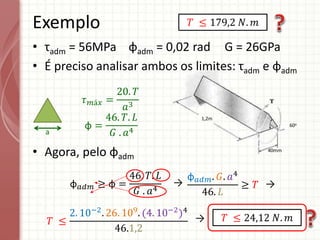
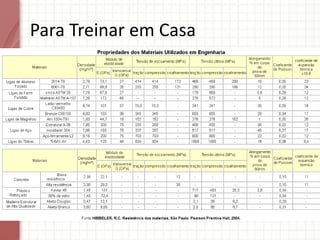
O documento apresenta um resumo sobre torção em barras. Discute conceitos como torque, rotação e fórmulas para cálculo de torção. Apresenta exemplos de problemas estaticamente indeterminados e explica a abordagem para resolvê-los. Por fim, discute limitações da teoria clássica para barras maciças de seção não circular.